考虑修理结构的舰船部署能力仿真

李宣池，胡俊波，张志华

考虑修理结构的舰船部署能力仿真

李宣池，胡俊波，张志华

海军工程大学理学院，湖北武汉430033

海上环境日益复杂，不仅要关心单艘舰船的部署能力，更要关心多艘舰船可同时部署的能力，以满足不同军事任务的用船需求。针对多艘同型舰船的部署能力问题，分析舰船入役时机、计划修理间隔期及修期控制等因素对同型舰船部署能力的影响，并从军事需求出发，提出多艘同型舰船部署能力的度量指标体系。在此基础上，建立多艘同型舰船部署能力的数学模型，给出同型舰船部署能力的仿真算法，较好地解决了同型舰船部署能力计算困难的问题。最后，通过仿真分析发现，舰船入役时机、计划修理间隔期及修期控制对同型舰船的部署能力具有较大影响，尤其是随着舰船计划修理间隔期的延长，其部署能力呈S形增加，对优化舰船修理结构，提高同型舰船部署能力，降低舰船维修保障费用具有重要意义。

舰船；部署能力；修理结构；仿真分析

期刊网址：www.ship-research.com

引用格式：李宣池，胡俊波，张志华.考虑修理结构的舰船部署能力仿真［J］.中国舰船研究，2015，10（5）：123-128.

LIXuanchi，HU Junbo，ZHANG Zhihua.Simulation analysis ofwarship dep loy ability withmaintenance structures involved［J］.Chinese Journalof Ship Research，2015，10（5）：123-128.

0　引言

舰船是一种大型的复杂海上作战平台，为充分发挥其作战效能，需要在入役初期根据舰船所承担的使命任务与装备修理需求合理编排舰船的修理结构，确定坞修、小修、中修等不同修理类别的修理时机，从而合理安排其全寿命周期内的各种修理活动。不仅如此，随着海上环境的日益复杂和军事任务的多样化，人们还关心多艘舰船可同时部署的能力，以保持多艘舰船处于可随时执行作战任务的状态，最大限度地满足不同军事任务的用船需求。

舰船部署能力与其修理结构密切相关。传统的舰船修理结构［1-2］是在考虑主要舰船装备修理需求的基础上，确定坞修、小修、中修的修理间隔期与计划修理活动的持续时间（即修期）。这种舰船修理结构编排方法针对的主要是单艘舰船，基本不考虑与其他同型舰船在作战部署与修理活动安排上的协调性，容易造成舰船计划修理活动与军事用船需求的不匹配，甚至还会出现某些时段无船可用的现象［2-3］。为有效解决舰船计划修理活动与军事用船需求的匹配问题，近年来，国内、外学者针对舰船修理结构的编排方法进行了大量研究［2-5］。张耀辉等［5-7］在舰船修理级别、修理时间与修理间隔期等方面进行了优化调整，以便更加准确地预测装备修理需求，有效控制舰船各类计划修理类别的修期，但没有考虑舰船使用需求对舰船修理结构的影响。美海军自2003年开始实施舰队反应计划以来，对舰船修理结构的编排方法进行了大量研究，尤其是针对美军航母编队维修问题，提出了集划分模型［1-2，8］和二层网络流模型［9］等编队修理计划的编排方法，有效延长了编队的修理间隔期，提高了舰船部署时间。朱晓军等［10］分析了编队使用需求对单舰修理结构制定的影响，通过时间序列法对舰船修理结构进行优化研究，建立了编队条件下舰船修理结构的优化模型，在编队所属舰船相对固定的情况下，对提高编队在航率具有重要意义。

本文将针对多艘同型舰船部署能力问题，在分析舰船入役时机、计划修理间隔期及修期控制等因素对同型舰船部署能力影响的基础上，从军事需求出发，提出多艘同型舰船部署能力的度量指标体系。针对军事用船特点，建立至少1艘在航率、至少2艘在航率及至少k艘在航率（以下简称k艘在航率）的数学模型，客观反映多艘同型舰船满足不同军事任务的能力。同时，为方便同型舰船部署能力指标的计算，研究k艘在航率的仿真算法，以较好地解决同型舰船部署能力指标计算困难的问题。最后，通过仿真分析舰船入役时机、计划修理间隔期及修期控制对同型舰船部署能力的影响。

1　同型舰船部署能力度量指标及影响分析

1.1舰船部署能力度量指标

同型舰船部署能力是指某型舰船处于随时执行战备任务状态的数量，以满足不同军事需求。当同型舰船只有1艘时，其部署能力实际上是该舰船全寿命周期内的在航总时间与舰船服役时间之比，也就是通常所指的舰船在航率。对于多艘同型舰船而言，其部署能力是指在同型舰船的共同服役时间（即服役稳态期）内，至少有1艘舰船可部署能力、至少有2艘舰船可部署能力，以及至少有k艘舰船可部署能力等，以满足不同战备任务的用船需求。其中，至少有1艘可部署能力是该型舰船随时可执行一项军事任务的可能性，至少有k艘可同时部署能力是该型舰船可同时执行k项军事任务的可能性。在实际中，至少有k艘舰船可部署能力通常用至少有k艘舰船在航率（以下简称“k艘舰船在航率”）来表示，即在n艘同型舰船的服役稳态期内，保持至少有k艘舰船同时在航的时间与稳态期时间之比。

1.2同型舰船部署能力的影响因素分析

在舰船全寿命周期内，其一般处于在航和修理2种状态。其中修理活动包括在航期间的临时修理和计划修理。由于临时修理主要是针对个别舰船装备的修理活动，故修理持续时间较短（临时修理中，如出现严重故障，由于其发生的概率较小且产生机理较为复杂，故本文暂不予考虑）。从这个意义上来看，影响同型舰船部署能力的最主要因素包括计划修理间隔期、计划修理持续时间（计划修期）和舰船入役时机等。

1）计划修理间隔期对部署能力的影响分析。计划修理间隔期是指一艘舰船2次计划修理之间的在航时间。由单艘舰船在航率定义可以看出，传统意义上的舰船在航率随计划修理间隔期的延长线性增加，但对于多艘同型舰船的部署能力，随着计划修理间隔期的延长，尽管k（k=1，2，…，n）艘在航率是增加的，但由于各艘舰船的计划修理时机会出现交叉现象，使得k艘在航率与计划修理间隔期呈现出非线性现象。由下文第4节的实例分析将可以看出，k艘在航率与计划修理间隔期之间呈S形增加。

2）计划修期对部署能力的影响分析。对单艘舰船而言，舰船计划修期越长，其在航率便越小。由于舰船计划修理活动涉及范围大、持续时间长，为有效控制计划修期，需要合理安排、交叉实施各种修理活动。从这个意义上看，计划修理活动具有很大的随机性，具体表现为舰船坞修、小修、中修的修期是一个随机变量。设 X1，X2，X3分别表示舰船坞修、小修、中修的修期，通常认为其是服从正态分布的随机变量。

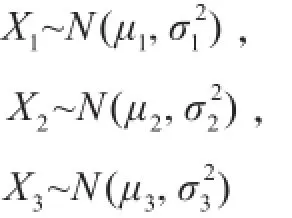
其中：μ1，μ2，μ3分别为舰船坞修、小修和中修的平均修期；σ1，σ2，σ3分别为坞修、小修和中修持续时间的标准差，反映各类计划修理活动持续时间的波动。各类计划修理活动的安排越周密，σ1，σ2，σ3就越小，特殊地，当 σ1=σ2=σ3=0时，说明坞修、小修和中修活动是完全按照预定的修理计划实施各项修理任务。

3）舰船入役时机对部署能力的影响分析。对多艘同型舰船而言，由于其修理结构是相同的，因此，为保持随时有多艘舰船可以部署，必须交错安排每艘舰船的计划修理活动。显然，在舰船修理结构确定的情况下，舰船不同的入役时机对交错实施舰船计划修理活动具有很大的影响，甚至会出现无船可用的现象。

2　舰船部署能力数学模型

2.1单舰全寿命周期状态的数学描述

以某型舰船为例，在全寿命周期内的修理结构为：入役—坞修—小修—坞修—中修—……—坞修—退役。为方便起见，通过矩阵MC来表达舰船修理结构，si为舰船所处的状态，ti为舰船处于si状态的持续时间，如t2为舰船处于状态s2（小修）下的持续时间。

对单艘舰船而言，根据周期修理结构，si∈U，U表示舰船在服役期内所处的几种状态：

2.2同型舰船状态数学描述

对于同型舰船而言，同样可以利用矩阵方法描述各艘舰船在服役稳态期内的各种状态。若某型舰船共有n艘，按照入役的先后顺序进行排列，可以得到同型舰船的状态矩阵：

同型舰船的状态矩阵F_MC有关符号说明：

1）m表示第1艘舰船在稳态期内所经历状态的个数；m'表示第n艘舰船入役时所有同型舰船所处的状态。

2）tij表示第i艘舰船第 j个状态的持续时间（i=1，…，n；j=1，…，m）。例如，t11表示第1艘舰船入役后所处第1个状态（部署状态）的持续时间，t12表示第1艘舰船首次进行坞修的持续时间。由于第n艘舰船是在第1艘舰船处于第m'个状态时才入列，因此，tn1=…=tnm'-1=0，tnm为第1艘舰船退役时第n艘舰船所处的状态。

3）由于第n艘舰船是在第1艘舰船处于第m'个状态时才入列，因此，n艘同型舰船的服役稳态期实际上是第n艘舰船入役时间到第1艘舰船退役时间，为同时服役时间。因此，服役稳态期T可表示为

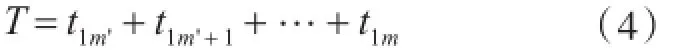
2.3舰船可部署能力数学模型

为有效提高同型舰船部署能力，需合理安排多艘同型舰船的修理活动，以便最大限度地满足军事需求。根据同型舰船部署能力定义，本节将建立k（k=1，…，n）艘舰船在航率的数学模型，并给出其计算方法。

1）1艘舰船在航率的数学模型。

对于n艘舰船而言，其第i艘舰船在任意时刻t所处的状态可表示为

当 fi（t）=1（i=1，2，…，n）时，表示第i艘舰船在时刻t处于可部署状态；当fi（t）=0（i=1，2，…，n）时，表示第i艘舰船在时刻t处于修理状态。则

是一个只取0或1的示性函数。当 f（t）=0时，表示在时刻t至少有1艘舰船处于可部署状态；当f（t）=1时，表示n艘舰船在时刻t同时处于在修状态。由此可得，n艘同时在修的总时间Y1为

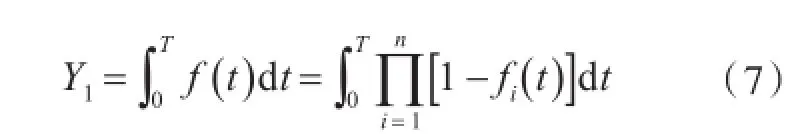
显然，Y1是一个随机变量，其数学期望为n艘同型舰船同时处于在修的平均时间，即

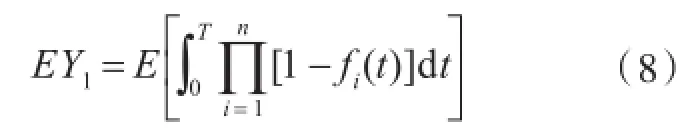
因此，1艘在航率P1可表示为

2）k艘舰船在航率的数学模型。

为获得k艘在航率，需要计算至少有k艘舰船同时在航的总时间。由式（5）可知，恰好有i（n-k＜i≤n）艘舰船在时刻t同时处于在修的状态可表示为

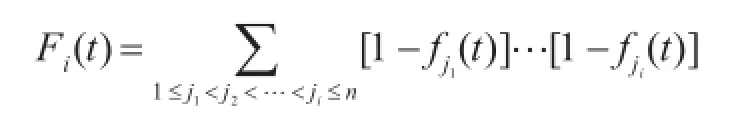
因此，至少有n-k+1艘舰船在时刻t同时处于在修的总时间为

显然，Yk是一个随机变量，其数学期望为至少有n-k+1艘舰船同时在修的平均时间，即

从而可得到k艘在航率为

3　部署能力的仿真算法

由于各艘舰船在某时刻是否处于在航状态具有随机性，因此，给同型舰船部署能力的计算造成了很大困难，所以，本节将建立同型舰船部署能力的仿真模型，给出同型舰船部署能力的仿真算法。具体仿真过程如下。

1）确定n艘同型舰船的入役时间。

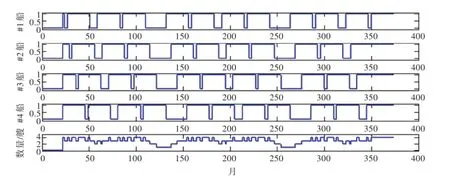
图1　稳态期内舰船状态情况仿真Fig.1　Simulation results of the ships in steady-state

2）随机产生修理间隔时间。在舰船实际使用过程中，由于执行任务的影响，常常会造成舰船等级修理间隔时间为随机变量。假定等级修理间隔时间服从均值为 μ0、方差为的正态分布，则可以随机产生舰船在2次等级修理之间的在航时间。例如，对于第1艘舰船，利用正态分布N（μ0，σ02）可以随机生成m+1/2随机数，其中第1个随机数即为第1艘舰船入役到首次坞修的在航时间，记为t11；第2个随机数即为第1次坞修到第1次小修之间的在航时间，记为t13。

3）随机产生修理持续时间。按照坞修、小修、中修持续时间服从的分布函数，分别产生坞修、小修、中修的持续时间，从而可以获得n艘同型舰船结构矩阵F_MC。

4）利用结构矩阵F_MC和式（4）计算得到服役稳态期T。

5）利用结构矩阵F_M C和式（7），就可以得到至少有1艘舰船在航的总时间Y1，从而由式（8）得到至少有1艘可部署能力为P1=Y1/T。

6）类似地，利用式（11）和式（12）可以得到至少有k艘舰船可部署能力为Pk。

7）将上述步骤2）～6）重复进行1 000次仿真，并对每次得到的1艘舰船可部署能力、k艘舰船可部署能力进行平均。

4　实例分析

现有某型舰船4艘，舰船全寿命周期为374月，其修理结构为：入役—坞修—小修—坞修—中修—坞修—小修—坞修—中修—坞修—小修—坞修—退役。其中坞修修期为3个月，小修修期为8个月，中修修期为22个月，计划修理间隔期为24个月。同时假设4艘舰船先后入役的时间间隔为5个月、7个月和10个月。根据上述假设，对各艘舰船在稳态期内所处状态进行仿真（图1，其中共同服役时间以第4艘舰船入役的时间为起点，之前4艘舰船所处状态不考虑，统一记为0），并可以统计得到同型舰船在航率。

4.1舰船入役时机对部署能力影响分析

在同型舰船中，每艘舰船的入役时间不同，对舰船部署能力的影响如表1所示。以第1艘舰船入役时间为基准，当第2、第3、第4艘舰船入役时间间隔分别相差2，4，3个月时，1艘舰船在航率为0.963 0，3艘舰船在航率为0.774 9，4艘舰船在航率为0.552 7。而当第2、第3、第4艘舰船入役时间间隔分别相差4，8，6个月时，1艘舰船在航率为0.988 3，3艘在航率为0.842 1，4艘在航率为0.394 8。显然，最后1艘舰船入役的时间与第1艘舰船入役时间间隔越小，就越容易造成同型舰船同用同修的情况，4艘同时在航的概率就越大。

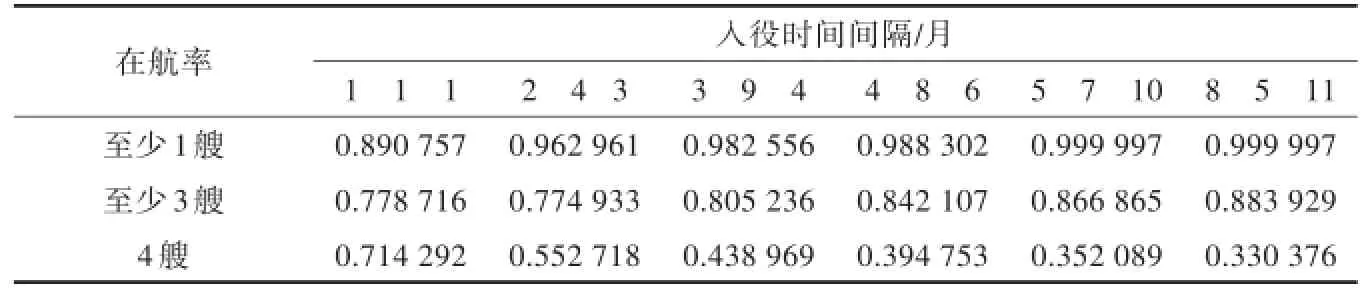
表1　不同入役时间间隔对舰船在航率的影响Tab.1　In fluences of different service tim e intervals to rate of sailing

4.2计划修理间隔期对部署能力影响分析

在给定4艘舰船入役时间间隔分别为5，7，10个月的情况下，将计划修理间隔期从16个月逐步增加到30个月，仿真同型舰船的部署能力（图2）。仿真发现：当修理间隔期从16个月逐步增加到30个月时，至少有1艘舰船的在航率接近为1；至少有2艘舰船和至少有3艘舰船的在航率呈S形增长趋势，并且在20～22个月之间出现增长拐点。即在计划修理间隔期小于20个月时，至少有2艘舰船、至少有3艘舰船的在航率快速增加；在计划修理间隔期大于20个月时，至少有2艘舰船、至少有3艘舰船的在航率增加缓慢。由此可见，延长计划修理间隔期可以提高同型舰船部署能力，但过于增大计划修理间隔期会造成在航期间装备临时修理任务量的增大，同时对提高同型舰船的部署能力也十分有限。

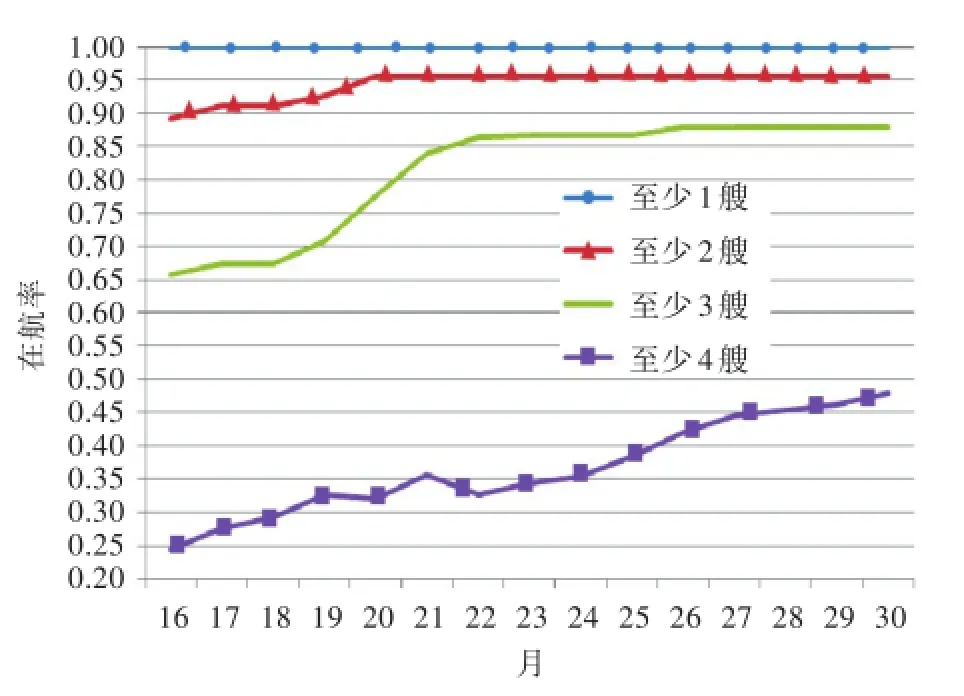
图2　延长修理间隔期对在航率的影响Fig.2　Influence ofextending the repairing intervals to the rate ofsailing

4.3计划修期对部署能力影响分析

舰船计划修理持续时间（修期）的波动与计划修理活动的管理密切相关。为反映计划修期的波动对舰船部署能力的影响，给定舰船修理间隔期为24个月，对于不同的计划修理类别，同时改变各类计划修理持续时间的方差进行仿真（图3）。随着修期方差的增大，同型舰船在航率随之降低，尤其对至少3艘、至少4艘在航率的变化较为明显。因此，为有效提高同型舰船部署能力，需要科学制定修理计划，严格控制修理活动，以便尽可能减小误差。

图3　改变修理持续时间的方差对在航率的影响Fig.3　The influence of changing repairing time to the rate ofsailing

5　结语

针对同型舰船部署能力的问题，本文首先研究影响舰船部署能力的主要因素，给出了不同军事用船需求下舰船部署能力的数学模型。由于模型计算复杂，因此采用的是实例仿真方法。计算结果表明：在实际使用中，合理编排舰船修理结构，科学组织维修保障活动，严格执行各项任务计划，能够最大限度地提高舰船部署能力，以应对瞬息万变的海上战场。

［1］ ROLAND JY，JOHN F S，JAMESG K.Aircraft carrier maintenance cycles and their effects［R］.Santa Monica：RAND，2008.

［2］ROLANDLY J Y，RAJ R，JESSIE R.Impacts of the fleet response p lan on surface combatantmaintenance［R］.Santa Monica：RAND，2006.

［3］HALL M.The impact of long-term aircraft carrier maintenance scheduling on the fleet readiness p lan［D］.California：Naval Postgraduate School，2004.

［4］ BROWN R L，LAWPHONGPANICH S，SCHRADY D，et al.Forward engagement requirements for US naval forces：new analytical approaches［R］.Washington，DC：Deputy Chief ofNaval Operations，1997.

［5］张耀辉，郭金茂，单志伟，等.装备预防性维修的维修级别逻辑决策分析方法［J］.装甲兵工程学院学报，2008，22（5）：40-44.

ZHANG Yaohui，GUO Jinmao，SHAN Zhiwei，et al. Maintenance level logic decision analysis method of preventivemaintenance［J］.Journal of Academy of Armored Force Engineering，2008，22（5）：40-44.

［6］ 程志君，郭波.连续劣化系统的最佳检测与维修策略分析［J］.系统工程与电子技术，2008，30（1）：193-196.

CHENG Zhijun，GUO Bo.Analysis of optimal inspection and maintenance policy for continuous deteriorating system［J］.Systems Engineering and Electronics，2008，30（1）：193-196.

［7］ 何春雨，金家善，孙丰瑞.基于LINGO软件的舰船装备修理级别优化分析［J］.上海交通大学学报，2011，45（1）：78-82.

HE Chunyu，JIN Jiashan，SUN Fengrui.Optim ization model of ship's equipment LORA based on LINGO［J］. Journal of Shanghai Jiaotong University，2011，45（1）：78-82.

［8］ YARDLEY R J，KALLIMANIJG.A methodolgy for estimating the effect of aircraft carrier operational cycles on the maintenance industrial base［R］.Santa Monica：RAND，2007.

［9］YARDLEY R J，KALLIMANI JG.Increasing aircraft carrier forward presence：changing the length of the maintenance cycle［R］.Santa Monica：RAND，2008.

［10］朱晓军，张涛，彭飞，等.基于编队时间序列的舰船修理结构模型［J］.系统工程与电子技术，2012，34（11）：2285-2289.

ZHU Xiaojun，ZHANG Tao，PENG Fei，et al.Model ofmaintenance structure of ship based on time series of fleet［J］.Systems Engineering and Electronics，2012，34（11）：2285-2289.

［责任编辑：喻菁］

Sim u lation analysis ofwarship dep loy ability w ithm aintenance structures involved

LIXuanchi，HU Junbo，ZHANGZhihua
College of Science，Naval University of Engineering，Wuhan 430033，China

Asmarine environment becomes increasingly complex，the deployment of warships in different military tasks，including both singlewarship deployment aswellasmulti-warship coordination，isoften discussed.This paper analyzes themain factors that influence the deploy ability ofwarships of the same type when the warship comes into service，plans repairing interval，schedules control and etc.Based on the analysis，themeasurement indicators for concurrent dep loy ability of identicalwarships are constructed，and the correspondingmodel and the simulation algorithm is provided.The proposed approach is seen to be a good solution to the difficulties in calculating concurrent deploy ability.Finally，the simulation results suggest thatall the factors are of vital significance to the deploy ability；particularly，as themaintenance interval increases，the deploy ability shows S-shape growth.In brief，this app roach p lays a significant role for optim izing maintenance structures，promoting the deploy ability of identical warships and reducing the maintenance cost.

warship；dep loy ability；maintenance structure；simulation analysis

U674.7

ADOI：10.3969/j.issn.1673-3185.2015.05.020

2015-01-04网络出版时间：2015-10-8 10∶43

李宣池（通信作者），男，1990年生，硕士生。研究方向：海军装备效能评估与保障优化。E-mail：309904546@qq.com

张志华，男，1965年生，博士，教授。研究方向：武器系统保障工程和可靠性工程

网络出版地址：http∶//www.cnki.net/kcms/detail/42.1755.TJ.20151008.1043.004.htm l