船舶拖曳潜体回转和收放作业仿真
2015-08-24马文彬向祖权茅云生
马文彬,向祖权,茅云生
船舶拖曳潜体回转和收放作业仿真
马文彬1,2,向祖权1,2,茅云生1,2
1武汉理工大学高性能船舶技术教育部重点实验室,湖北武汉430063 2武汉理工大学交通学院,湖北武汉430063
为了对潜体拖曳系统的运动进行预判,并能快速且正确地得到船舶拖曳的潜体在水下不同时刻的位置和缆绳形态图,采用改进的集中质量法对拖曳系统进行数学建模,模拟水下拖曳系统不同工作状态下的运动形态,并对潜体的回转作业和收放作业进行简化。结果显示:水下拖曳潜体做回转运动时,拖曳潜体系统形成闭合的圆形回路;做收放运动时,拖曳系统随着时间的增加长度逐渐增加,从而完成潜体的收放操作。通过对海上船体拖曳系统运动规律的预测,以及对拖体拖曳系统的直航、回转和收放工况的研究,得到了拖曳系统的缆形的实时分布,以及潜深和拖曳潜体系统最大拉力之间的大小对应关系。
潜体;集中质量法;回转;收放
期刊网址:www.ship-research.com
引用格式:马文彬,向祖权,茅云生.船舶拖曳潜体回转和收放作业仿真[J].中国舰船研究,2015,10(5):34-40.
MAWenbin,XIANG Zuquan,MAO Yunsheng.Simulation of the towed bodyunder turningand retraction[J].Chinese Journalof Ship Research,2015,10(5):34-40.
0 引言
水下拖曳潜体不仅被应用于科研工作和资源开发,在现代化战争中,其也已成为军事作战的主要武装力量。由于在科研、勘探和作战过程中会遇到很多海峡、障碍及暗礁等,故水下潜体的操纵性问题一直是各国研究的重点,在水下潜体入水执行任务[1-2]和从水中收起[3]时,会遇到各种问题,因而对拖曳潜体系统动态响应的预判和仿真是解决问题的关键。
潜体在水下的动态响应是通过系泊于工程船舶后的柔性钢缆进行连接控制的。为了能够准确地对水下潜体的动态响应进行预判,本文将通过数值仿真对海洋拖曳缆绳拖挂潜体的系统进行仿真,采用改进的集中质量法模拟柔性钢丝缆,耦合潜体一起做运动,图1即为拖曳潜体系统工作的示意图。
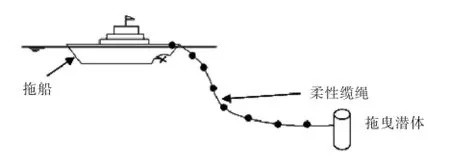
图1 潜体工作示意图Fig.1 Working diagram ofa towed body
1 拖曳潜体方程
要预判和仿真水下潜体的运动响应,首先须对水下潜体建立数学模型。潜体在水中为六自由度运动,但在收放及拖曳过程中,对其的建模和计算需要遵照以下假定:
1)潜体处于直立状态,并且拖曳角度为定值,即潜体运动仅考虑在3个局部坐标系下的平行运动。
2)对拖体进行升力和阻力计算时,将其简化为一个球体。
3)在潜体收放过程中,假定新增加的微元段以固定的角度计入缆绳。
1.1潜体方程
对于潜体在水中的运动,首先假定不考虑实际海况与风浪流的影响,其次假定潜体处于直立状态。将潜体的运动与拖曳刚性缆绳进行耦合,联立成拖曳系统进行计算。图2所示为潜体受力分析图。

图2 潜体受力分析图Fig.2 Stress analysisofa towed body
根据达朗伯原理,在一个系统内,如果所有的约束力因为虚位移而做的虚功总和为零,则该系统内的每一个粒子所受到的外力与惯性力的矢量之和,与虚位移的点积总合起来也为零。即
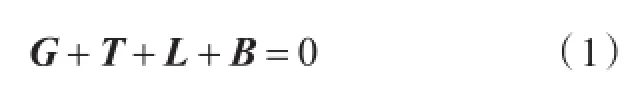
式中:G为潜体在水中的重量;T为柔性缆绳对潜体的拉力;L为作用在潜体上的流体力;B为惯性力。
其中,潜体重量G为

式中:md为潜体的质量;ρ为流体密度;Vd为潜体的体积;g为重力加速度;t为拖曳缆绳的切向方向;n,b为拖曳缆绳对应切向方向的2条相互垂直的法线方向。
柔性钢丝缆绳对潜体的拉力为

作用在潜体上的流体力为:
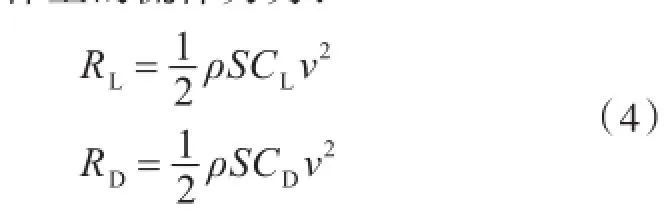
式中:RL为潜体受到的升力;RD为潜体受到的阻力;S为潜体的侧面积;v为来流速度;CL和CD分别为升力系数和阻力系数。
潜体的惯性力B为

式中:Δmd为潜体的附加质量;v˙t,v˙n,v˙b分别为潜体在缆绳空间上t,n,b方向上的速度。
1.2用改进集中质量法求解刚性缆绳
采用集中质量法[4-6]建立拖曳系统模型,并假设系缆是由许多个集中质量点和无质量的弹簧单元构成。集中质量所在的点称为节点,将系缆看成是分为n段的结构,其动力平衡方程根据牛顿第二定律列出,第1段在水下部分与拖体、锚或各种潜水器相连,最后一段与船体相连。
传统的集中质量法是在考虑系泊钢丝绳的重力、浮力、流体拖曳力、附连水质量以及系泊钢丝绳的惯性力等因素的基础上,通过牛顿第二定律来建立各个钢丝绳节点之间的微分方程。假设钢丝绳的重力和浮力都作用在集中质量点上,微元杆均无质量仅传递拉力而不传递扭矩。集中质量法的缺点在于,求解拖曳系统时,需计算庞大的刚性非线性方程组,而由于数值解法的限制,其对于可稳定求解的时间步长产生了很大限制。
所谓改进的集中质量法,即运用牛顿第二定律得到动力方程。有限差分法的不足之处在于,对时间和空间进行差分得到的非线性方程组较为复杂,所以本文将采用集中质量法得到的动力方程,结合钢丝绳的运动方程,对拖曳潜体系统进行求解,但前提是钢丝缆绳的微元长度和时间步长大小都是固定值,从而减少方程数量,以便根据精度要求进行计算。质量节点的受力分析图如图3所示。
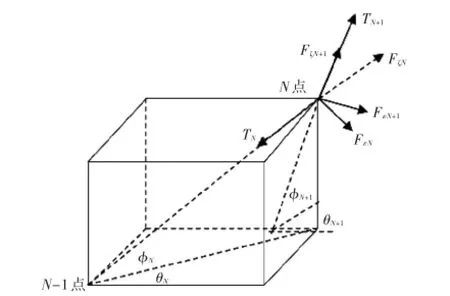
图3 缆绳节点受力图Fig.3 Stressanalysis ofa cable node
根据牛顿第二定律,可得到第i点的运动方程为
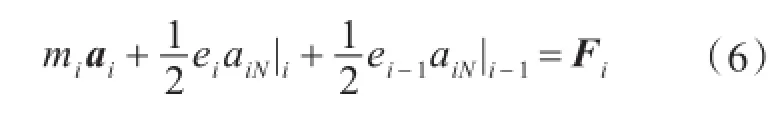
式中:mi为钢丝缆绳节点质量;ai为节点加速度;aiN|i-1和aiN|i分别为加速度矢量在两个相邻单元上的法向分量,其中N代表第N个微元段;ei为第i个质点的附加质量;Fi为节点受到的合力,包括重力、浮力、拖曳力和系泊张力。
在固定坐标系下,将i节点的动力方程展开
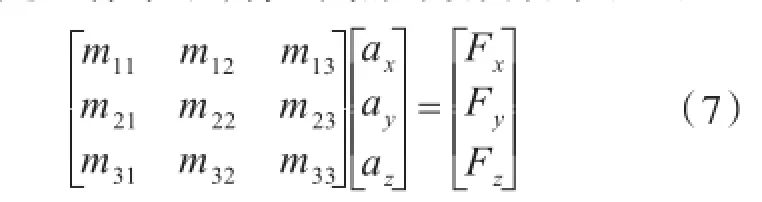
附加质量的加速度为

其中:ex=cosφsinθ,ey=cosφcosθ,ez=sinφ。
由式(7)和式(8),得

式中,Fx,Fy,Fz为节点在3个坐标系方向下的分力。
传统的集中质量法需要反复修正才能得到模拟结果,这样会大大增加工作量。在此处,引入水下潜体的运动平衡方程与动力平衡方程来组成非线性的方程组,以达到求解的目的。潜体拖曳钢丝缆绳的运动平衡方程为:

由此,可得潜体钢丝缆绳拖曳系统的运动方程为:
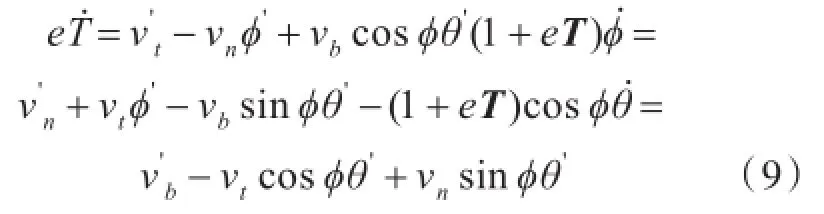
式中,e为拖曳潜体微元段的附加质量。
2 拖曳潜体运动仿真
拖曳潜体在水中的运动主要包括2大类:回转和收放[7]。本文首先从原理的角度分析回转和收放问题,然后求解特定的工程问题。计算结果可用于拖曳潜体的预报。
2.1拖曳潜体的船舶回转运动
拖曳潜体的船舶在做回转运动时,会对水下潜体有一定的影响,所采用的计算方法是用上一时刻的值去求解下一时刻钢丝缆绳的形态。但是,船舶的多次转向同时也改变着钢丝缆绳在上一时刻的迭代初始值。拖曳潜体回转运动示意图如图4所示。

图4 回转运动示意图Fig.4 Schematic of turningmotion
假定船舶拖曳的潜体在做回转运动时,回转圆是由无数个微元直径构成,而拖曳轨迹则是以无数个直线段的形式模拟圆形拖曳过程。图5即为求解拖曳潜体的船舶做回转运动时的计算原理图,即此时固定于船舶上的坐标系发生转动,沿z轴旋转ϑ,故坐标变换矩阵为
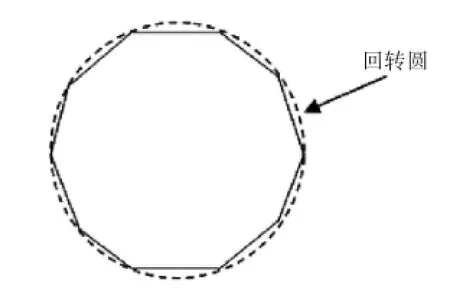
图5 回转计算原理图Fig.5 Schematic diagram of turning computing

式中:x0,y0和z0为转换前的坐标值;xn,yn和zn为转换后的坐标值;ϑ为船舶回转时的角速度。
质量节点的初始值为(T,vt,vn,vb,θ,φ),所以速度矢量在经过坐标变换以后T不变化,但是角度会发生变化,即如下式:

式中:(Ttn,vtn,vnn,vbn,θtn,φtn)为转换后的值;(T,vt,vn,vb,θ,φ)为节点初始坐标参数。
2.2拖曳潜体的缆绳收放运动
当钢丝缆绳的长度是固定的时,常出现各种问题,但在实际操纵中,钢丝缆绳的收放问题才是重点,因为它决定了水下潜体的位置、运动状态、速度以及对障碍物的躲避。当其长度不固定,而是通过船舶逐渐放入水中(收起)时,在h时刻缆绳的长度取决于卷筒绞车收放潜体的速度:

式中:LH为H时间段内部的水下缆绳的总长度;v′h为h时刻缆绳释放的瞬时速度。
最初,是将湿钢丝缆绳的长度设定为0,因此,要将缆绳当成固定长度分成固定的数目不可能。由于集中质量法的研究方法中每一个分段的长度需要为定值,故湿缆绳微元(节点)的数目须随时间逐渐增加。
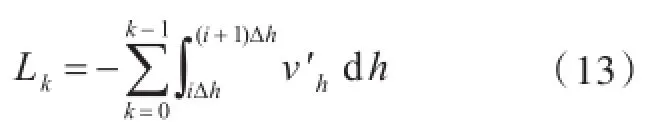
式中,Lk为kΔh时刻水下缆绳的总长度。图6即为拖曳潜体系统在收放过程的基本原理图。

图6 收放计算原理图Fig.6 Schematic diagram of retractable computing
尽管从理论上讲,新增加的分段不可能完全浸没在水中,但改进集中质量法的方程依然适用,其前提是分段微元的长度不能太大。尽管新增分段在建模方法上与实际不相符,但考虑到新增分段的长度相对于整条钢丝缆绳的长度,其仿真误差是可以忽略的。
将改进的集中质量法应用到钢丝缆绳的最后一个节点(Lj,hk+1)上,即可得到下面的边界方程:

式中:L为水下缆绳的总长度;E为缆绳的弹性模量;k为时间指数;j为节点编号;F为节点受到的合力;m为节点质量。
随着钢丝缆绳长度的增加,分段微元的数目增加,计算方程的数目也急剧增加,同时,计算时间也会急剧增加。一旦前一时刻的值已知,即可对下一时刻的值进行求解。采用数值解法求解钢丝缆绳的收放问题,步骤如下:
1)初始化:设定时间步长、微元步长和仿真计算的截止时间。缆绳长度从0到指定长度,初始值即为时间为0的时刻。
2)根据改进的集中质量法建立相邻时刻方程。
3)采用迭代计算方法代入初始值,循环求解钢丝缆绳的下一时刻。
4)将时间指数k转换到k+1。
5)如果k≤TIME/Δh(TIME为收放的总时间长度),则进行下一次循环,否则,循环停止。
3 数值计算与结果讨论
选取进行仿真计算的船舶、拖体和钢缆的参数信息如表1所示。
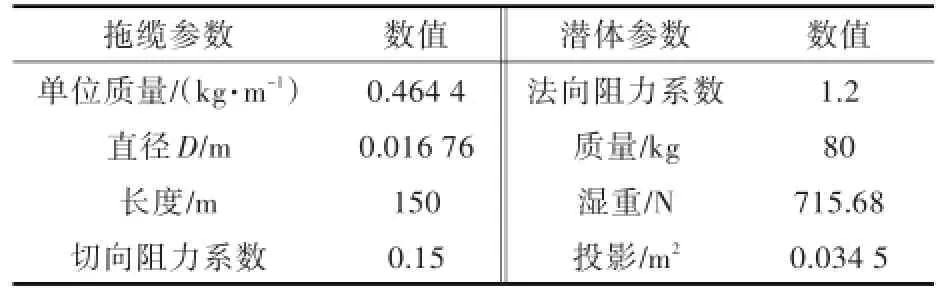
表1 计算参数Tab.1 Calculationalparam eters
3.1拖曳潜体的船舶直航运动
拖曳潜体的直航状态是最常见的潜体操纵状态。起始状态为:设定拖曳系统处于垂直静止状态,规定船舶速度在30 s内达到1.336 5 m/s,然后,船舶以该恒定速度航行至500 s。计算结果如图7~图9所示,计算间隔时间为10 s。
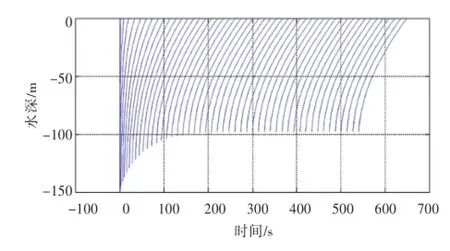
图7 水下拖曳潜体钢丝缆绳形态图Fig.7 Cable shapes of the underwater towed body

图8 水下拖曳潜体最大潜深图Fig.8 Maximum diving depth of the underwater towed body
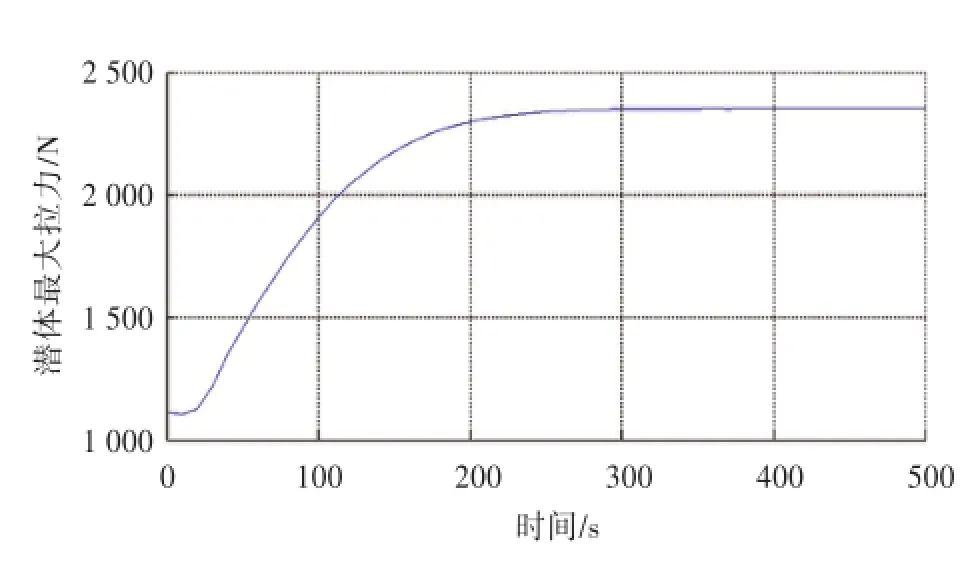
图9 水下拖曳潜体最大拉力图Fig.9 Maximum cable tension of the underwater towed body
由计算结果可知:
1)潜深随速度的增加而减小,最后趋于一个稳定的值而达到平衡。
2)拖曳系统的最大拉力发生在船舶的拖点处。该最大拉力在初始时刻会由于惯性而轻微变化,然后会在短时间内急剧增大,最后趋于一个峰值。
3.2拖曳潜体的船舶回转运动计算
回转运动(此处仅是从船舶运动受力分析的角度出发,没有考虑舵与螺旋桨的影响)可以通过对线速度、角速度和回转半径等参数的控制来选择其对水下潜体的影响,此处,仅通过回转线速度参数来研究其影响因子。表2为在不同的回转半径之下,拖曳船舶选定的线速度、角速度和回转周期列表。

表2 拖曳潜体船舶回转运动计算参数Tab.2 Calcu lation param eters of turningm otion for the tow ing vessel
初始条件为:假定水下潜体以及钢丝缆绳处于竖直状态,船舶运动在30 s内其速度由0加速至目标速度值。图10所示的计算结果是不同回转半径下船舶和拖曳潜体在水平方向上的轨迹点图。图中横向坐标和纵向坐标为回转海域平面(单位:m)。图11所示为船舶做回转运动时拖曳系统的三维图形,图12所示为船舶做回转运动时拖曳系统的水平方向的缆形分布放大图。图13所示为拖曳潜体潜深轨迹图,图14所示为拖曳系统最大拉力变化图,计算间隔时间为10 s。
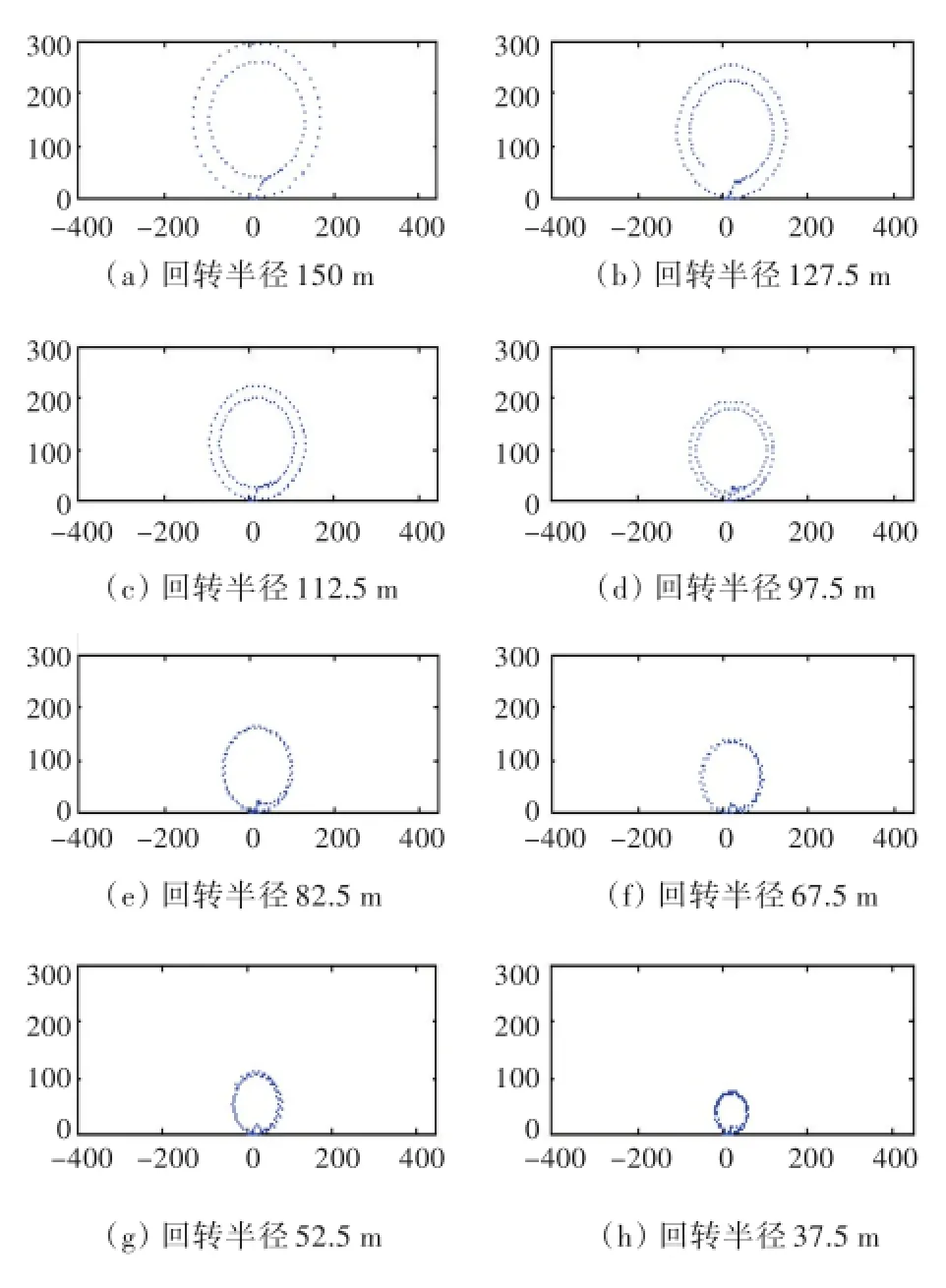
图10 船舶与潜体的回转运动轨迹图(外圈为船舶轨迹,内圈为潜体轨迹)Fig.10 Trajectories of turningmotion of the ship and the towed body(the outer ring is for the ship,inner locus for the towed body)
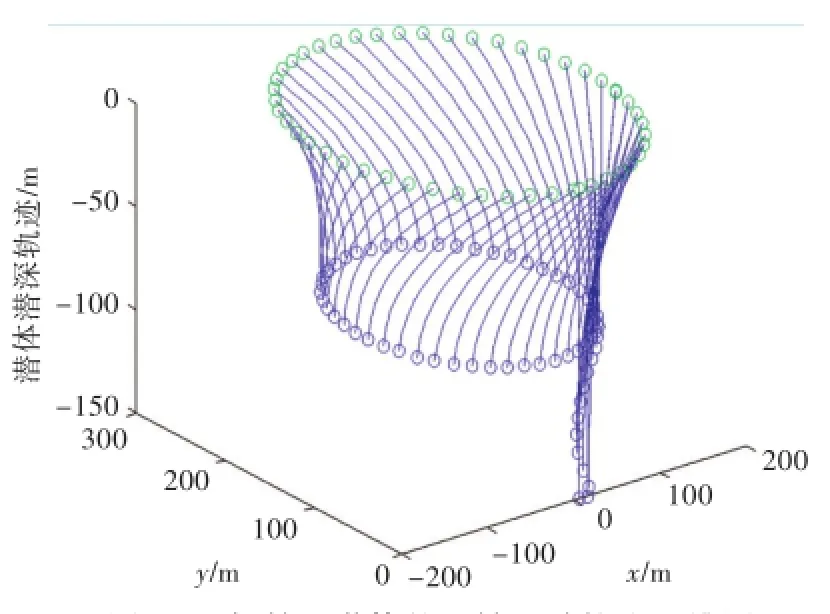
图11 船舶和潜体的回转运动轨迹三维图(上圈为船舶轨迹,下圈为潜体轨迹)Fig.11 Three-dimensional trajectories of turningmotion of the ship and the towed body(the upper ring is for the ship track,the following locus for the towed body)
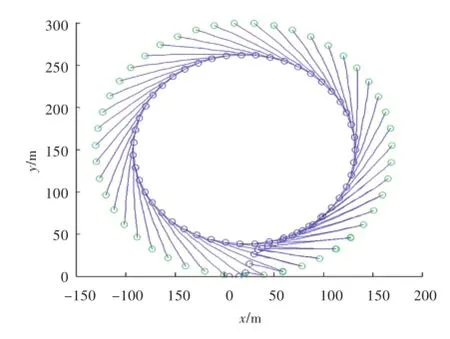
图12 船舶和潜体的回转运动轨迹俯视图(外圈为船舶轨迹,内圈为潜体轨迹)Fig.12 Vertical view of turningmotion trajectories of the ship and the towed body(the outer ring is for the ship,inner locus for the towed body)
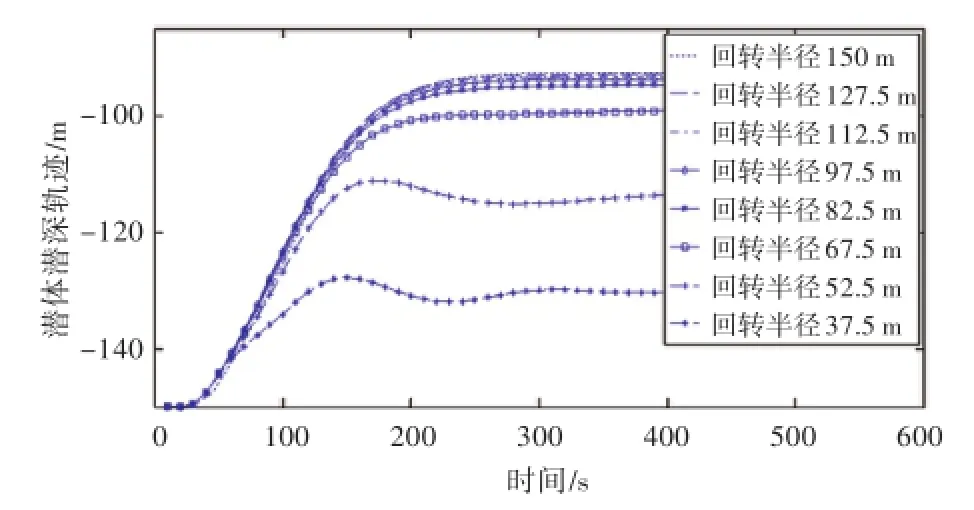
图13 拖曳潜体的潜深轨迹图Fig.13 Diving depth trajectories of the towed body

图14 拖曳系统最大拉力变化图Fig.14 Underwater cablemaximum tension of the towing system
结果分析:
1)潜体在被拖船拖曳的过程中,潜体轨迹位于船舶轨迹内部,也呈圆形。计算结果符合已经被证实的闭环理论,即拖曳潜体在拖曳回转的过程中拖曳缆阵形成一个封闭的运行轨迹图。
2)拖曳半径越大,在相同的速度下,潜体的最大潜深便越小,拖曳系统的最大拉力越大,也即拖曳缆绳对潜体提供的拉力越大,则潜体的操纵响应也越大。
3)拖曳轨迹越大,潜体的波动便越小,反之,潜体在回转过程初期会有较大的潜深波动。潜体形成的闭环越小,拖曳缆绳就越容易在实际过程中缠绕,在理论计算初期便会形成波动,所以回转半径的选择不能小于船舶船长的3倍。
4)潜体的潜深轨迹与拖曳系统的最大拉力图具有一致性,即力决定拖曳系统的整体位移。
3.3拖曳潜体收放过程计算
拖曳潜体的收放运动包含2个过程:一是潜体和钢丝缆绳的收放过程;二是潜体及钢丝缆绳收放完成后的平衡过程。一般来说,对于收放过程中的拖曳潜体,在收放结束后是不可能完全平衡的,还需要一定的时间来平衡,其平衡过程的计算与直航运动计算类似,但初始值设定为释放钢丝缆绳结束时的数据[8-10]。潜体拖曳系统的钢丝缆绳总长50m,根据收放理论,对钢丝缆绳的运动进行模拟仿真。拖曳潜体释放缆绳的工艺中包含2个相继发生的过程,即缆绳的释放过程和拖曳系统的平衡过程。图15所示为释放的缆长总长度为150 m时的释放过程缆形图,其中深色为释放过程,浅色为平衡过程,其计算间隔时间为10 s。图16所示为不同速度下拖曳潜体释放过程轨迹图。图17所示为不同速度下拖曳潜体拖点处拉力的变化规律。
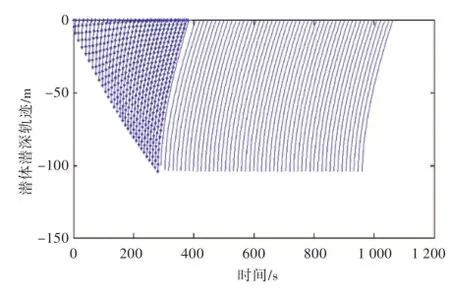
图15 拖曳潜体释放全过程运动图Fig.15 The diving depth trajectory of the towed body during the releasing process
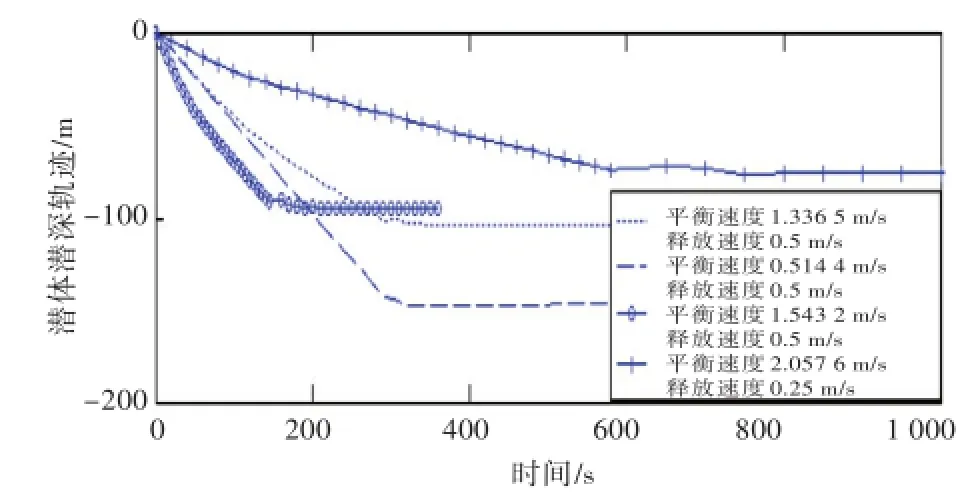
图16 不同速度下拖曳潜体释放过程轨迹Fig.16 The diving depth trajectory of releasing the towed body atdifferent speeds
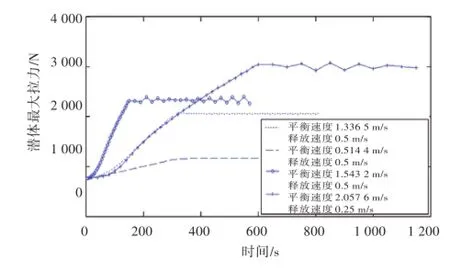
图17 不同速度下拖曳潜体拖点处拉力变化图Fig.17 Maximum tension of the towing system atdifferen speeds
由计算可知:
1)潜体释放过程包括释放和平衡2个阶段。
2)拖曳缆形与拖曳最大拉力具有一致性。
3)拖曳速度越大,拉力越大,最大潜深越小。
4)释放速度越快,拉力增加越快。
4 结论
1)对水下拖曳潜体运动响应的预判,可通过改进的集中质量法来模拟实现。经计算,发现船舶拖曳潜体系统随着拖曳速度的增加其最大潜深会变小,最大拉力值变大,并且最大拉力的位置即为船舶拖点处,拖曳系统的缆形与拉力存在一致性,所以在拖曳过程中,拖点是最容易造成缆绳断裂的位置。
2)船舶收放过程包含2个时间上相互连接的阶段,即不完全收放阶段和完全收放后的平衡阶段,其主要原因是因为船舶速度大,在给定的时间步长内拖曳潜体系统无法平衡,因此在拖曳钢丝绳完全释放后,需要额外的时间来平衡系统。
3)考虑到拖曳系统所处的复杂海况,风、浪、流等载荷会对拖曳系统的运动产生一定的影响,所以进一步计算的方向就是将风、浪、流加载到拖曳系统中,这有利于提高水下潜体运动响应预判的准确性。
[1]孙霄峰.单船中层拖网系统的建模与仿真[D].大连:大连海事大学,2008.
[2]高霓.微小型水下潜器近自由液面操纵性预报[D].哈尔滨:哈尔滨工程大学,2013.
[3]高勇.水下潜器突防空间建模方法研究[D].哈尔滨:哈尔滨工程大学,2013.
[4] YUAN Z J,JIN L A.A dynam icmodel tomaintain the depth of underwater towed system[C]//2012 International Conference on System Science and Engineering(ICSSE),2012:499-504.
[5] SHIH C H,YAMAMURA S.Analysis of control structure for turning maneuvers[J].Mathematic Prob lem in Engineering,2010,1:3-4.
[6]马卫星.潜体运动兴波流场数值模拟方法研究[D].哈尔滨:哈尔滨工程大学,2008.
[7]陈钰.海洋内孤立波与潜体相互作用数值模拟研究[D].广州:华南理工大学,2010.
[8] 金良安,苑志江,迟卫,等.海洋拖曳系统对船舶操纵性能的影响[J].交通运输工程学报,2013,13(1):47-54.
JIN Liang'an,YUAN Zhijiang,CHIWei,et al.Influence ofunderwater towed system on ship maneuverability[J].Journal of Traffic and Transportation Engineering,2013,13(1):47-54.
[9]程楠.集中质量法在深海系泊冲击张力计算中的应用研究[D].天津:天津大学,2008.
[10]沈观林,胡更开.复合材料力学[M].北京:清华大学出版社,2006:29-130.
[责任编辑:卢圣芳]
Sim u lation of the towed body under turning and retraction
MAWenbin1,2,XIANGZuquan1,2,MAO Yunsheng1,21 Key Laboratory of High Performance Ship Technology ofMinistry of Education,Wuhan University of Technology,Wuhan 430063 2 School of Transportation,W uhan University of Technology,Wuhan 430063,China
This paper briefly describes the important role of underwater towed operation,but in its practical operation,the towed body turning and retractable jobs are of vital importance.By using the lumped massmethod,the towed body is simulated utilizing the p rinciples of calcu lus.W hen the turningmotion of the towing vesselacts on a towed body,the flexible cable connection will change accordingly.Moreover,different swing factors(boat speed)will also affect towing performance.Finally,this paper presents the detailed calculation of themovementof the potential towed body.
towed body;lumpedmassmethod;turning;retraction
U661.33
ADOI:10.3969/j.issn.1673-3185.2015.05.006
2014-12-26网络出版时间:2015-10-8 11∶10
工信部高技术船舶科研项目资助(201302HX12)
马文彬,男,1989年生,硕士生。研究方向:拖网渔船拖曳系统仿真。E-mail:wenbin_ma@whut.edu.cn
向祖权(通信作者),男,1974年生,博士,副教授。研究方向:船舶建造工艺。E-mail:zuquan_xiang@163.com
茅云生,男,1962年生,博士,教授。研究方向:船舶建造工艺。E-mail:958588928@qq.com
网络出版地址:http∶//www.cnki.net/kcms/detail/42.1755.TJ.20151008.1110.016.htm l
