基于源数估计的无约束欠定盲源分离算法

付永庆，郭慧，，苏东林，刘焱

(1.哈尔滨工程大学 信息与通信工程学院，黑龙江哈尔滨150001;2.北京航空航天大学电磁兼容技术研究所，北京100191)

盲源分离(blind signal separation，BSS)起源于鸡尾酒问题［1］，可在源信号和传输信道参数均未知的情况下仅根据源信号的统计独立性和观测信号来恢复源信号，被广泛应用于生物医学［2］、地质信号处理和分析［3］、图像处理［4］和移动通信［5］等领域。根据观测信号和源信号的数目关系，将盲源分离问题分为正定、超定和欠定3种情况。上述情况都以信源数目的正确估计为前提实现信号的分离。目前，在信源数目估计领域中，以前两种情况下的盲源分离为主，基于高阶累积量扩展了很多成熟的算法，而欠定盲源分离(undetermined blind signal separation，UBSS)方面的研究尚少。目前欠定盲源分离中信源数目的估计大多基于稀疏混合信号的线性聚类特点，如:2001年Bofill利用势函数的局部最大值的个数对信源数目进行估计［6］;2008年谭北海等直接利用概率统计知识，通过划分区域并统计观测点在不同区域的概率分布实现信源数目估计［7］;2009年张烨等提出采用拉普拉斯势函数判断其局部最大值达到源数估计的目的［8］。但这些方法都存在一些问题，如算法的抗噪声性和信号的稀疏性易受异常值的影响从而造成误判。针对上述问题，提出一种Hough加窗法，利用信号的稀疏特性，先确定经平滑后的聚类区域，减小异常值的影响，再寻找区域最大值，避免陷入局部最大，在此基础上对混合矩阵进行估计。针对信号分离问题，提出一种无约束分离算法，采用“内点法”选择合适的混合矩阵列向量作为初始迭代值，修正了现有算法对混合矩阵列向量的选取标准。

1 稀疏欠定盲源分离模型

通常欠定盲源分离的线性瞬时混合模型写作:

式中:X(t)为m个观测信号矢量，A为m×n维的混合矩阵，S(t)为n个源信号矢量，t=1，2，…，T为观测点时刻，当m＜n时即为欠定盲源分离。

为了实现欠定情况下的盲源分离，必须对源信号提出进一步的约束条件，假设源信号是稀疏信号，即源信号在绝大多数采样点的取值为零或接近于零，只有少数采样点的取值远离零［9］。假设在采样时刻t，只有s1(t)起主导作用，则有

观测信号可以看作:在以x1(t)…xm(t)为坐标轴的m维空间中，所有以源信号s1(t)为主导的采样时刻确定的一条直线，其斜率取决于混合矩阵A的第一个列向量 [a11，…，am1]T。如果混合矩阵A的任意m×m的子矩阵都满足可逆性，则每个源信号可确定一条直线。因此，源信号的数目估计就转化为对观测空间中直线的条数估计。

实际应用中，很多信号具有稀疏特性，或者可以通过适当变换(如短时傅里叶变换，STFT)［10］、Gabor变换［11］、小波变换［12］等)使得信号在变换域中满足稀疏特性。

2 Hough加窗法

2.1 Hough 变换

Hough变换原用于图像的匹配，将原图中给定形状的所有点都集中到变换空间中的某些位置，形成峰值点。基于该思想，把观测信号空间中直线的检测问题转化为寻找变换空间中峰值点的问题。

观测数据可看作m维空间中经过零点的一条直线［13］，据此构造转换关系，将观测信号空间中的直线转换成变换空间中的角度变换量［14］:

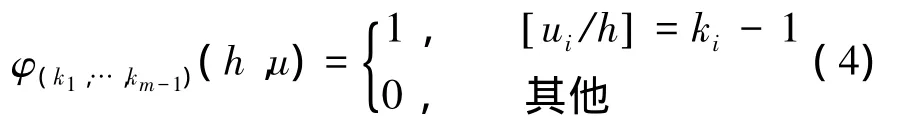
式中:k=1，…，π/h，表示高维直方图的分区数目，h是Hough变换的量化步长，k越大，即h越小，变换量的分类精度越高;在变换量的每一个分类中，i=1，…，m－1，包含了变换量的所有维数，[·]表示比·小的最大整数。则落入高维直方图某一区域的变换量数目为:

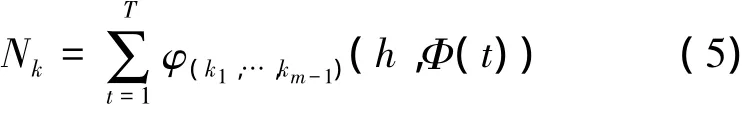
2.2 加窗法

得到变换量的直方图后，若直接检测峰值点容易陷入局部最大值。为此对直方图做加窗处理。由于m维的观测信号经Hough变换后变为m－1维变换量，故对其加m－1维的超方体窗。加窗的目的是平滑直方图中的异常值，得到聚类区域。加窗后重新计算变换量的分类统计数为

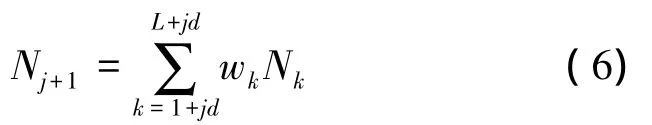
式中:j=0，…，[π/hd]－[L/d]+1表示重新计算后的变换量分类数，L表示超方体窗口的边长，d表示超方体窗口沿观测空间每个坐标轴方向的移动步长表示权重，由落入直方图某一区域中的变换量数占变换量总数的比率获得。

对新的直方图搜索峰值即可得到源数的估计。峰值对应的角度变换估计量与混合矩阵元素有式(7)的关系，由此得到混合矩阵的估计值:

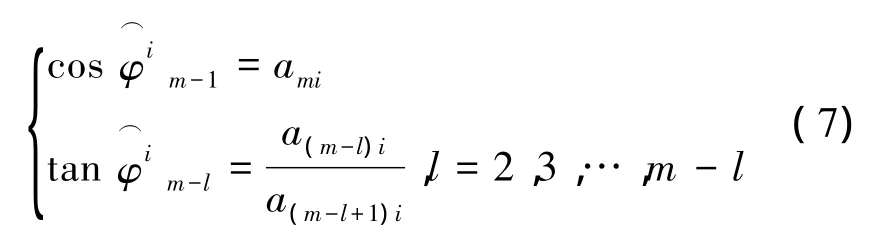
式中:ami表示混合矩阵第m行i列的元素。

3 无约束分离算法

3.1 无约束问题

文献［2］中分离混合信号有如下的约束条件:

由于式(1)可写为

式中:Am称作混合矩阵Am的满秩因子，Amn－m称作混合矩阵Am的余式因子。又有

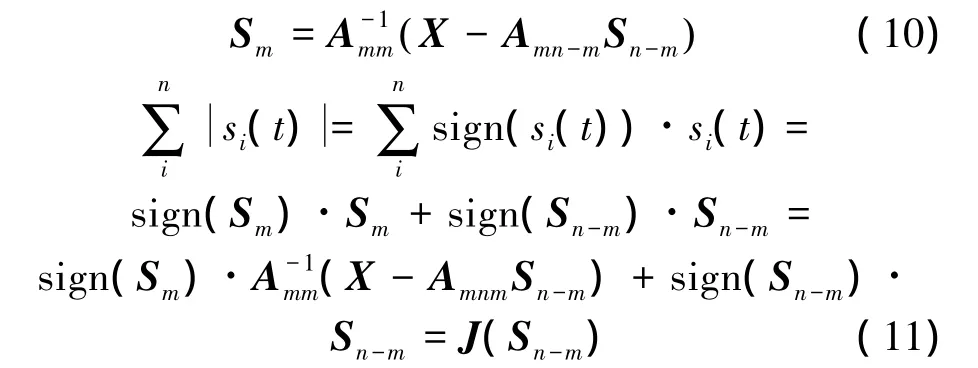
式中:sign(·)表示取·的符号。因此，可以将式(8)带约束的优化问题转化为上述无约束优化问题，要满足，令J(Sn－m)对Sn－m求导，即

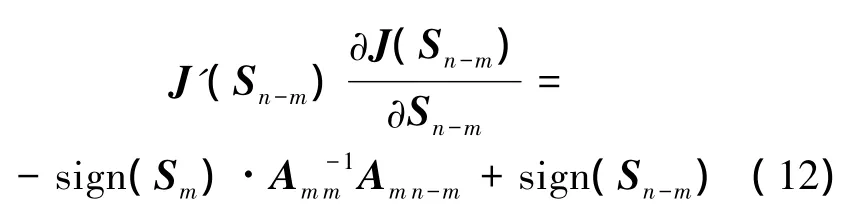
3.2 初始迭代值选取

初始迭代值的选取直接影响算法的迭代次数和收敛速度，因此，需要合理选择初始值。现有算法通过选择观测点与混合矩阵列向量夹角最小的前m列作为分离矩阵，该方法并不适用于任何情况。

图1 二维矢量分解示意图Fig.1 Schematic diagram of 2D vector decomposition

如图1所示，以两个混合信号为例，在单位化对称化后的散点图中，混合信号x与列向量a1、a2的夹角最小，但是其分解矢量的长度和远大于混合信号x在列向量a2、a3上的分解矢量。这是因为当两个列向量分布于混合信号的同一侧时，有一个分解矢量必在其中一列向量的反方向上，此时，分解矢量与观测信号的夹角并不是最小。

根据散点图分布采用“内点法”选取初始迭代值。首先，令混合矩阵单位化和对称化，且使混合矩阵第一行和混合信号第一行数据符号为正。然后，去处混合矩阵和混合信号第一行数据后绘制散点图，以混合信号为原点，混合矩阵列向量分布在其四周。从n个点中选取m个点，这m个点围成的多边形应能包含混合信号点。从满足要求的组合中选择与混合信号夹角和最小的作为满秩因子Am，否则按照最小夹角法选取Am，其余列向量作为余式因子An－m，Sm则由式(10)得到，令Sn－m=0。

源信号越稀疏，J'(Sn－m)值越小，在迭代过程中，分离信号逐渐逼近源信号S，稀疏性增强，J'(Sn－m)逐渐减小，当J'(S(k+1)n－m≥J'()时迭代终止，第k次迭代计算得到的即为分离信号。

4 仿真实验

4.1 算法性能评价标准

4.1.1 泛化交扰误差

采用泛化交扰误差(generalized crosstalking error，GCE)评价混合矩阵的估计精度。定义如下:

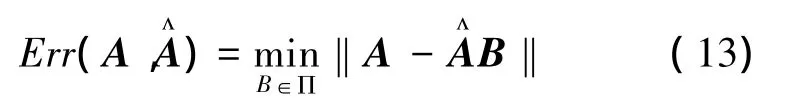
式中:Π表示所有n×n维可逆矩阵组成的集合，表示与一个尺度矩阵和置换矩阵的乘积，以消除的幅度不确定性和排序不确定性。当且仅当和A完全等价时，Err(A，)=0。

4.1.2 信干比

信号分离后第i个源信号si和分离信号的信干比(signal to interference radio，SIR)定义为:

盲源分离的幅度具有不确定性，在计算信干比前需先确定源信号si和分离信号的幅度因子λi:

通过式(15)使得si和的幅度尽量一致。在该度量下，信干比SIR越大，说明分离信号越接近源信号。

4.1.3 互相关系数

互相关系数(cross correlation coefficient，CCC)描述两个信号的相似性，定义为

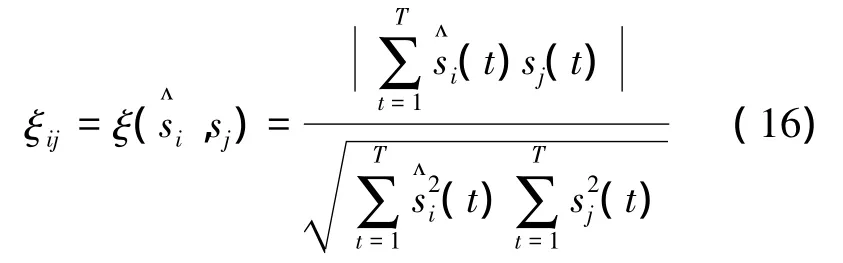
式中:sj为源信号，为还原信号。在该度量下，ξij=1和0分别表示与sj完全相似和不相似。

在上述3个标准中，泛化交扰误差和互相关系数都是与特定值做比较(GCE值与0比较，CCC值与1比较)，可以体现单独算法的有效性，但因其计算值很小，在多算法性能比较时不利于突出算法的差异，因此采用信干比来衡量不同算法的性能。

4.2 实验及结果分析

4.2.1 实验一:验证Hough加窗法的性能

为了验证信号稀疏度对算法的影响，需构建稀疏度可度量的稀疏信号。满足广义Gaussian分布的信号，其概率密度函数为:

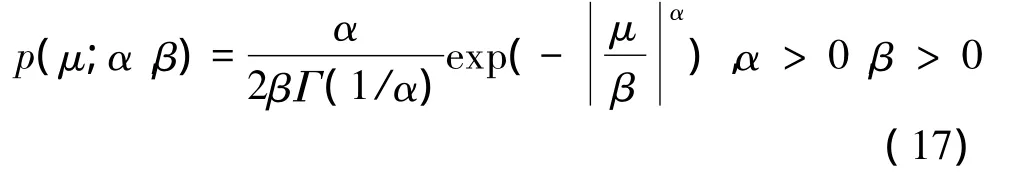
据此构建信噪比为40 dB，α＜1.5的稀疏度不同的广义Gaussian分布的随机信号和α=1，信噪比不同的信号，采样值T=5 000，随机选取2×6的混合矩阵得到混合信号，分别进行100次蒙特卡洛运算，分析算法的正确率，如图2所示。

图2 源数估计的正确性Fig.2 Accuracy of the source number estimation

Hough加窗法在稀疏性度量值为1.2及以上时，算法的正确率较低，在稀疏性度量值小于1.1和信噪比大于2 dB时算法正确率分别可达81%和85%以上，在稀疏性度量值小于0.8和信噪比大于15 dB时算法正确率达到100%。可见算法对信号的稀疏敏感性较低，且具有较好的抗噪声性能，即使在低信噪比下也能以较高的正确率估计出信源数目。

源数估计的高正确率保证了算法的稳定性。选取源数估计正确的情况估计混合矩阵，计算泛化交扰误差取平均值，并与势函数法、K均值法进行比较，得到不同算法下噪声和稀疏度对混合矩阵估计性能的影响图，如图3和图4所示。

从两幅图中看出，无论是在低信噪比下还是低稀疏度下，Hough加窗法得到的混合矩阵的泛化交扰误差都很小，趋近于0，尤其是在稀疏度为1.2以下和信噪比为8 dB以上时，混合矩阵估计精度更高，性能明显优于其他算法。势函数法直接对累计量进行峰值搜索，无法平滑奇异值对峰值检测的影响，因此性能不如Hough加窗法，K均值法由于受初始点选取的影响较大，故估计性能最差。

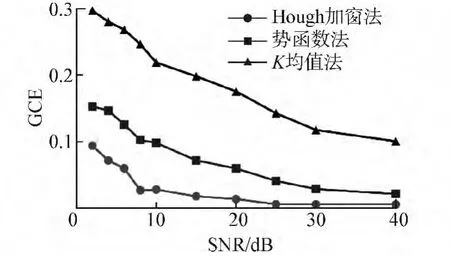
图3 噪声对混合矩阵估计精度的影响Fig.3 The influence of noiseon the accuracy of the estimation of mixing matrix

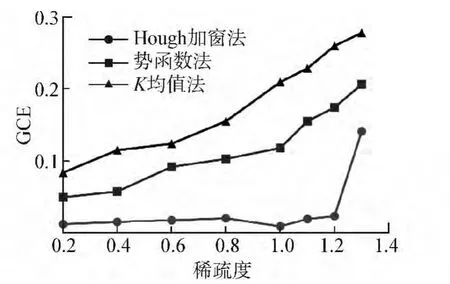
图4 稀疏度对混合矩阵估计精度的影响Fig.4 The influence of sparse on the accuracy of the estimation of mixing matrix

4.2.2 实验二:验证无约束分离算法的性能

在实验一得到的混合信号基础上，假设混合矩阵已知，信噪比为40 dB，α=1的情况下，通过互相关系数和信干比两个指标来评价算法的性能，如图5所示，并从分离信号的信干比、时间频度、复杂度和运行时间等方面，将本文算法与最短路径法、最小l1范数法进行比较，结果如表1所示。

图5中信噪比为40 dB时，互相关系数平均值达到0.991 8，对应的信干比平均值为169.65。整体来说，在信噪比较低的情况下，互相关系数可达到0.74以上，在信噪比为15 dB以上时，互相关系数达到0.9以上。在2～40 dB的范围内，信干比的数值波动在37 dB左右，约占最佳信干比值的21.9%。表明无约束分离算法自身具有分离准确性较高，抗噪声性能较好的特点。

表1给出了无约束分离算法与其他2个有约束算法的性能比较结果。其中时间频度以m个混合信号，n个源信号，采样值为T的情况进行计算，k表示无约束分离算法的迭代次数。3种分离算法得到的源信号信干比值均一样，说明了本文算法的正确性。从时间频度上看，最短路径法值最小，最小l1范数法最大。本文算法与最小l1范数法相差一个系数，本文算法的k取值一般为1～3，最小l1范数法在本实验中取值为15，运行时间也证明了上述分析。在运算时间上，本文算法不及势函数法，但适用范围要大于势函数法，因为势函数法只适用于两个混合信号的情况。因此，综合运行时间和适用性可以得出:无约束分离算法具有较好的性能。

表1 算法比较结果(α=1，SNR=40 dB)Table 1 The comparison results of different algorithms(α =1，SNR=40 dB)

图5 混合分离的分离性能Fig.5 Performance of signal separation

为了验证“内点法”修正了最小夹角法对混合矩阵列向量的选取标准，将无约束分离算法与基于最小夹角法的分离算法进行比较，结果如图6所示。

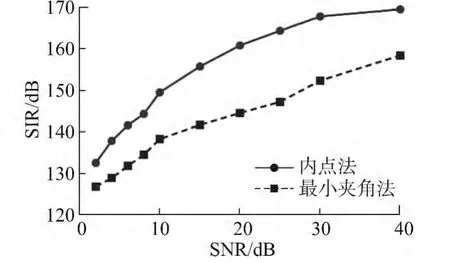
图6 内点法与最小夹角法的性能比较Fig.6 Performance comparison of signal separation between interiorpoint method and minimum angle method

在混合矩阵选取的过程中，不同的混合信号出现列向量散点包含混合信号散点的情况是不确定的，因此，针对不同的混合信号而言，内点法较最小夹角法的性能优势表现的也不尽相同。在图6中，内点法的优势较最小夹角法比较突出，且在信噪比较高时，这种优势更明显。

4 结论

1)针对现有混合矩阵估计算法易受噪声干扰，对信号稀疏性要求较高等问题，提出一种Hough加窗算法，利用稀疏信号的特性，用加窗的方法平滑因噪声或稀疏性差造成的异常值，对得到的聚类区域分别寻找最大值，达到全局最大值搜索的目的，峰值的个数即为信源的数目。

2)针对现有分离算法带约束的优化问题，提出一种无约束的分离方法，并采用“内点法”来选择合适的初始迭代值，修正了现有算法对混合矩阵列向量的选取标准。

仿真结果不但验证了算法的有效性，还表明了算法具有较好的抗噪声性、较低的稀疏敏感性。若信号不满足稀疏特性，可对其采用适当的变换使其在变换域中具有稀疏性，该算法在变换域中仍适用。

［1］COMON P.Independent component analysis:a new concept［J］.Signal Processing，Special Issue on Higher Order Statistics，1994，36(3):287-314.

［2］MAMMONE N，La FORESTA F，MORABITO F C.Automatic artifact rejection from multichannel scalp EEG by wavelet ICA［J］.IEEE Sensors Journal，2012，12(3):533-542.

［3］TAKAHATA A K，NADALIN E Z，FERRARI R，et al.Unsupervised processing of geophysical signals:a review of some key aspects of blind deconvolution and blind source separation［J］.IEEE Signal Processing Magazine，2012，29(4):27-35.

［4］BADAWI W K M，CHIBELUSHI C C，PATWARY M N，et al.Specular-based illumination estimation using blind signal separation techniques［J］.IET Image Processing，2012，6(8):1181-1191.

［5］YANG Xiaomei.The application of blind signal separation in mobile communication［C］//2011 3rd International Conference on Computer Research and Development(ICCRD).Shanghai，China，2011:274-277.

［6］BOFILL P，ZIBULEVSKY M.Underdetermined blind source separation using sparse representations［J］.Signal Processing，2001，81(11):2353-2362.

［7］谭北海，谢胜利.基于源信号数目估计的欠定盲分离［J］.电子与信息学报，2008，30(4):863-867.TAN Beihai，XIE Shengli.Underdetermined blind separation based on source signals’number estimation［J］.Jour-nal of Electronics＆ Information Technology，2008，30(4):863-867.

［8］张烨，方勇.基于拉普拉斯势函数的欠定盲分离中源数的估计［J］.信号处理，2009，25(11):1719-1725.ZHANG Ye，FANG Yong.A new method to estimate the number of the sources for underdetermined blind separation based on lapulacial potential function［J］.Signal Processing，2009，25(11):1719-1725.

［9］邱天爽，毕晓辉.稀疏分量分析在欠定盲源分离问题中的研究进展及应用［J］.信号处理，2008，24(6):966-970.QIU Tianshuang，BI Xiaohui.Spares component analysis and application for underdetemined blind source separation［J］.Signal Processing，2008，24(6):966-970.

［10］BOFILL P，ZIBULEVSKY M.Blind separation of more sources than mixtures using sparsity of their short-time fourier transform［C］//Second International Workshop on Independent Component Analysis and Blind Signal Separation.Espoo，Finland，2000:87-92.

［11］CORDERO E，NICOLA F，RODINO L.Sparsity of gabor representation of schrodinger propagators［J］.Applied and Computational Harmonic Analysis，2009，26(3):357-370.

［12］MA Jianwei，PLONKA G，CHAURIS H.A new sparse representation of seismic data using adaptive easy-path wavelet transform［J］.IEEE Geoscience and Remote Sensing Letters，2010，7(3):540-544.

［13］HIROYUKI S，YUZO H.Blind source separation by a geometrical method［C］//Proceedings of the International Joint Conference on Neural Networks.Honolulu，USA，2002:1108-1114.

［14］付宁，彭喜元.K-Hough欠定盲信道估计算法［J］.电子测量与仪器学报，2008，22(5):63-67.FU Ning，PENG Xiyuan.K-Hough underdetermined blind mixing model recovery algorithm［J］.Journal of Electronic Measurement and Instrument，2008，22(5):63-67.

［15］何昭水，谢胜利，傅予力.信号的稀疏性分析［J］.自然科学进展，2006，16(9):1167-1173.HE Shaoshui，XIE Shengli，FU Yuli.Sparse analysis of signal［J］.Progress in Natural Science，2006，16(9):1167-1173.