短距绕组轴向磁阻式旋转变压器的优化分析

尚静，王昊，李婷婷，郝艳玲

(1.哈尔滨工业大学电气工程系，黑龙江哈尔滨150001;2.哈尔滨工程大学自动化学院，黑龙江哈尔滨150001)

磁阻式旋转变压器是近年来快速发展的一种旋转变压器。其无刷、无耦合变压器式结构，使其无需维护。与传统转子绕线式旋转变压器相比，使用可靠、寿命长、对机械和电气噪音不敏感。因此广泛应用在高温、严寒、潮湿、高速、高震动等旋转编码器无法正常工作的场合，如机器人系统、机械工具、汽车、电力、冶金、纺织、印刷、航空航天等领域［1-5］。目前磁阻式旋转变压器常见的结构为变气隙长度变磁阻式结构，其转子呈现波纹状凸极式轮廓。我国的上海21所、日本的多摩川公司、西安微电机研究所对该种变气隙磁阻式旋转变压器进行较深入研究且已有批量生产［6-9］。但是，这种变气隙的磁阻式旋转变压器的整机测角精度相对偏低，偏心问题与平均气隙磁阻的影响也比较大［10-12］。

轴向式磁阻式旋转变压器为一种等气隙长度变磁阻式结构。其轴向变磁阻式旋变结构与电磁原理与其他已有旋变相比，具有特殊性。由于气隙径向长度均匀，可以有效地降低平均气隙磁阻的影响。转子导磁环磁路结构使气隙磁阻互补，减少系统偏心影响，其磁路结构为轴向与径向的混合磁路结构。因此，轴向式磁阻式旋转变压器不仅能够节省空间体积，而且测角精度相对较高。

1 结构以及运行方式说明

短距分布绕组轴向磁路旋转变压器由定子、转子、正弦信号绕组、余弦信号绕组及励磁绕组构成，定子与转子间具有相等的气隙。

转子包含导磁材料与非导磁材料两部分，导磁材料按正弦规律周期性分布于转子中部，包含p个波峰与p个波谷，转子的两端为非导磁材料。正弦信号绕组、余弦信号绕组及励磁绕组设置于定子齿上。其中，正弦信号绕组、余弦信号绕组采用双层短距分布绕组，分别间隔地缠绕在4p组绕组齿上，缠绕于每组绕组齿上的信号绕组同极同相，且同相同极的信号绕组正向串联，每对上齿与其所对应下齿上的信号绕组的匝数相同。图1为2对极短距分布绕组轴向磁路旋转变压器的结构拆分图。

图1 短距分布绕组轴向磁路旋转变压器Fig.1 Diagram of axial flux reluctance resolver with short pitch distributed windings

短距分布绕组轴向磁路旋转变压器采用单相激磁的工作方式，激磁电压为u1=U1·sin(ωt)，并使转子按照图2中所示方向逆时针旋转，得到两相信号绕组R1R2和R3R4的输出电压为:

式中:u2c、u2s为正、余弦输出电压;ku为电压变比;U1为输入电压幅值;ω为激磁频率;θ为转子转角。

图2 短距分布绕组轴向磁路旋变电气工作原理图Fig.2 Electrical principle diagram of axial flux reluctance resolver with short pitch distributed windings

2 结构参数的调整

2.1 气隙尺寸优化

旋转变压器的结构参数优化中，函数误差是一个重要指标，为一个电周期内实际电压值和理论电压值之差的最大值占理论输出电压幅值的百分比，函数误差本身并不好求取，但可以用输出电势中的谐波含量来代替。输出电势中的谐波含量越低，函数误差越小。

短距分布绕组轴向磁路旋转变压器气隙中的空间谐波磁场主要包括两部分:一部分是的绕组谐波磁场;另一部分是齿谐波磁场。定转子之间的气隙大小与绕组谐波磁场有关。因此，为了提高整机的测量精度，有必要选取合适的气隙尺寸。以二对极短距分布绕组轴向磁路旋转变压器为例，在短距分布绕组轴向磁路旋转变压器的主要尺寸、极对数、定子每组齿数、齿距比等参数不变的条件下，对不同气隙长度时的模型进行了有限元分析，两相信号绕组输出电动势及其包络线的分布情况如图3所示。

图3 信号绕组输出电动势及其包络线的波形Fig.3 Waveform of output EMF and its envelope of signal windings

图4 输出电动势幅值在不同气隙时的分布Fig.4 Distribution map of output EMF amplitude when the gap is different

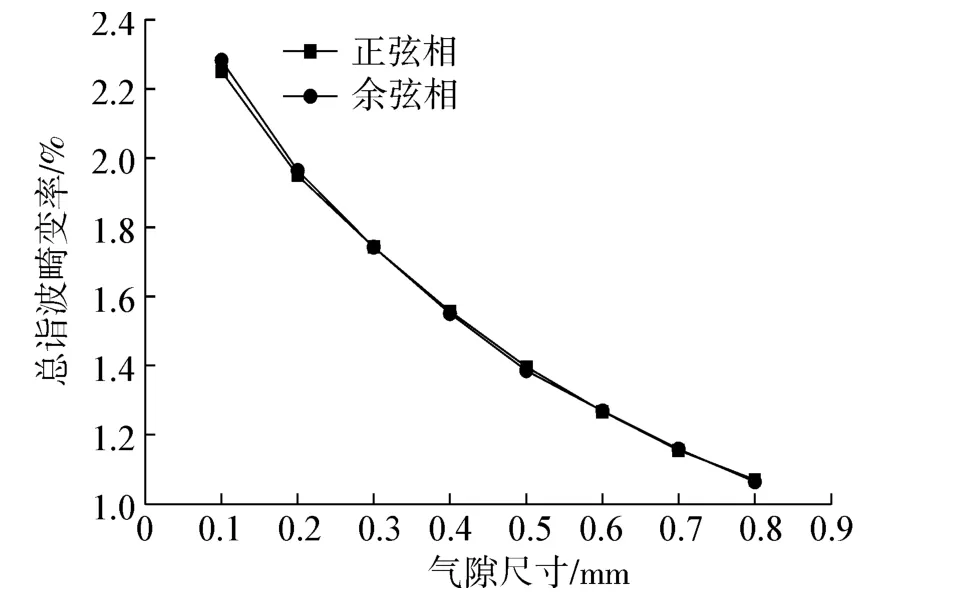
图5 总谐波畸变率在不同气隙时的分布Fig.5 The total harmonic distortion rate when the gap is different

图4与图5为二对极短距分布绕组轴向磁路旋转变压器输出电势幅值以及各次谐波含量在不同气隙长度条件下的变化规律。通过有限元软件与MATLAB软件的计算，结果表明信号绕组的输出电势幅值随着气隙尺寸的增大而明显下降，由于计算软件存在误差，所以两相信号绕组的总谐波畸变稍有不同，且变化规律并不平滑，总的谐波畸变率随气隙尺寸的增大呈下降趋势，且当气隙值超过0.4 mm时，总的谐波畸变率下降趋势开始变得缓慢。在制作样机时将根据实际的工艺技术要求以及短距分布绕组轴向磁路旋转变压器的技术指标来选取合理的气隙尺寸，以达到提高测量精度的目的。

2.2 定子齿数优化

短距分布绕组轴向磁路旋转变压器的定子齿数为4NP，其中N为每组齿数，P为转子极对数。当转子转动过程中气隙长度g保持不变，定子齿与转子的耦合面积按照正余弦规律变化，则气隙磁导按照正余弦规律变化。短距分布绕组轴向磁路旋转变压器一相信号绕组输出电势为

式中:Ns为励磁绕组每齿匝数，Λγ为γ次谐波磁导幅值;γ次谐波的绕组分布系数可以表示为

式中:Kyγ为γ次谐波的短距系数，Kdγ为γ次谐波的分布系数，q为每极每相的槽数，y为绕组节距，τ为极距。

于是，γ次谐波电势为

当气隙磁导中含有偶次谐波，即γ=2k，(k=1，2，3…)时，输出电势中相应的偶次谐波电势为

当定子齿数为4NP时，输出电动势对偶次谐波具有滤波作用。

下面考虑输出电势高次谐波中奇次谐波的大小，即 γ=2k+1，(k=1，2，3，…)时的谐波电势，γ 次谐波大小用γ次谐波含有率THDγ衡量由于此时γ次谐波电势与N和γ都有关，因此这里将对N和γ进行讨论。因此，γ次谐波含有率THDγ可以表示如下

当N≥5时，由于定子齿数太多会使旋转变压器的体积过大，安装难度提高。尤其是在极对数P≥2的情况下，定子齿数已经多达40。因此，在实际工程应用中取N≥5并不合适。

对于一对极短距分布绕组轴向磁路旋转变压器，分别建立N=1、2、3、4的模型，计算信号绕组输出电势并利用MATLAB软件对其包络进行FFT分析列于表1中。由于两相电势中谐波成分基本相同，所以这里只给出正弦相的奇次谐波含有率。

表1 一对极旋变不同每组齿数N时的各次谐波含有率Table 1 Each harmonic ratio of one pole pair resolver when each groups of teeth N are different

当N取不同数值时会影响输出电势中的高次谐波含量。经过推导得到，无论每组齿数N取什么值，输出电势中的恒定分量和偶次谐波都会被消除。当N＞1时输出电势中的奇次谐波将会被削弱。考虑到高次谐波中的主要成分是三次谐波，所以在设计定子齿数时尽量使每组齿数N=3，这样还可以避免输出电势中出现幅值较大的齿谐波。

2.3 极对数的影响

短距分布绕组轴向磁路旋转变压器的绕组采用双层短距分布绕组，节距为5。本文在短距分布绕组轴向磁路旋转变压器的主要尺寸、定子每组齿数、齿距比等参数不变的条件下，分别对极对数1、2、4等不同情况下的模型进行了有限元分析，得到了输出电势以及各次谐波含有率的普遍规律。不同极对数时各次谐波含有率如图6所示。

二对极与四对极正弦形转子轴向磁路旋转变压器的主要尺寸、定子每组齿数、齿距比等参数和一对极正弦形转子轴向磁路旋转变压器一致，只是极对数不同。

图6 奇次谐波含有率和极对数的关系Fig.6 The relationship between odd harmonic ratio and pole pairs

当忽视零位误差和两相幅值误差时，电气误差大小主要由函数误差即输出电势中的谐波含量决定。随着极对数的不断增加，输出电势波形大体相同，只是周期逐渐变小;随着极对数增加，输出电势中的各次谐波含量明显降低，其中三次谐波降幅很大，由一对极时的0.033 1分别降低到了0.018 6和0.014 0，降幅为43%和57%。五次谐波和七次谐波也有所降低，但因为它们的含量本来就较低，再加上软件的计算误差，所以降幅没有三次谐波大。

3 优化后的短距绕组轴向磁路旋转变压器谐波分析

通过对极对数、每极每相齿数以及气隙尺寸的优化分析，得出了不同结构时信号绕组输出电势的总谐波畸变率的分布情况。按照上述的分析结果，建立短距分布绕组轴向磁路旋转变压器的最优结构。在主要参数不变的条件下，选取极对数p为4，齿数N为3，气隙尺寸g为0.4 mm。利用Ansoft软件对这个4对极短距分布绕组轴向磁路旋转变压器进行有限元分析，结构模型如图7所示。

图7 4对极短距分布绕组轴向磁路旋转变压器的结构图Fig.7 Structure diagram of 4 pole pairs axial flux reluctance resolver with short pitch distributed windings

对优化后模型的输出电势包络线进行谐波分析，发现正弦相的总谐波畸变率为1.16%。其中，三次谐波含有率为1.03%，五次与七次谐波的含有率也有一些下降。五次与七次谐波占总的总谐波含量的比重很小，因此优化的结果对五次与七次谐波并不明显。由于正余弦信号绕组的设置相同，所以不需要再对余弦相进行谐波分析了。综上所述，通过结构优化的方法能够极大地削弱短距分布绕组轴向磁路旋转变压器的函数误差。

4 结论

本文提出了一种新型的短距分布绕组轴向磁路旋转变压器，并对它的结构及运行方式进行了说明。

1)在改变气隙的情况下，得到了输出电势的谐波含量与幅值的变化规律，并确定合理的气隙尺寸，降低函数误差。

2)针对不同绕组齿数进行了分析研究，考虑到体积与安装难度等因素的影响，发现当绕组齿数为3时，输出波形中各次谐波含有率最低，为实际模型的建立提供了一定的理论依据。

3)对不同极对数时输出电势中的谐波含量进行了比较，得出输出电势中的高次谐波含量随着极对数的增加而减小，可以有效的提高测量精度。

4)利用有限元分析法对优化后的短距分布绕组轴向磁路旋转变压器进行了仿真分析，总谐波畸变率有明显的下降，证明了优化措施的正确性与可行性。

［1］尚静，王昊，王伟强.多极轴向磁路磁阻式旋转变压器的分析与优化［J］.哈尔滨工业大学学报，2013，45(8):73-78.SHANG Jing，WANG Hao，WANG Weiqiang.Finite element analysis and structure optimization of the multipole axial flux reluctance resolver［J］.Journal of Harbin Institute of Technology，2013，45(8):73-78.

［2］周凯，焦文良，王志宏，等.磁阻式旋转变压器绕组结构分析［J］.信息技术，2013(1):61-65.ZHOU Kai，JIAO Wenliang，WANG Zhihong，et al.Winding structure analysis of variable reluctance resolver［J］.Information Technology，2013(1):61-65.

［3］周凯，王旭东，焦文良.磁阻式旋转变压器绕组结构设计与参数优化［J］.哈尔滨理工大学学报，2013，18(3):16-21.ZHOU Kai， WANG Xudong， JIAO Wenliang.Winding structure design and parameter optimization of variable reluctance resolver［J］.Journal of Harbin University of Science and Technology，2013，18(3):16-21.

［4］SHANG Jing，WANG Hao，CHEN Mimi，et al.The effects of stator and rotor eccentricities on measurement accuracy of axial flux variable-reluctance resolver with sinusoidal rotor［C］//E-lectrical Machines and Systems.Hangzhou，China，2014.

［5］董卫红.磁阻式旋转变压器设计［J］.机电工程技术，2015，44(3):44-47.DONG Weihong.Design of the variable reluctance resolver［J］.Mechanical ＆ Electrical Engineering Technology，2015，44(3):44-47.

［6］WANG Hao，CONG Ning，LI Tingting，et al.The decou-pling study on the dual-channel radial flux reluctance resolver with common magnetic circuit［C］//Electrical Machines and Systems.Hangzhou，China，2014.

［7］张健，吴忠，吴云涛.基于旋转变压器的伺服电机角位置及速度检测［J］.微电机，2013，46(11):22-28.ZHANG Jian，WU Zhong，WU Yuntao.Angular position and velocity demodulation for servo motor with resolver［J］.Micromotors，2013，46(11):22-28.

［8］KIM K C.Analysis on the charateristics of variable reluctance resolver considering uneven magnetic fields［J］.IEEE Transactions on Magnetics，2013，49(7):3858-3861.

［9］杨琪，施志勇.一种双旋转变压器测角系统设计［J］.现代雷达，2015，37(1):59-62.YANG Qi，SHI Zhiyong.Design of a double resolver angle measuring system［J］.Modern Radar.2015，37(1):59-62.

［10］HOU Chungchuan，CHIANG Y H，LO C P.Experimental verification of the resolver dynamic model and control designs［C］//Power Electronics and Drive Systems.Kitakyushu，Japan，2013.

［11］TANAKA K，SASADA I.A method of producing Z-pulse output from thin axial resolver［J］.IEEE Transactions on Magnetics，2013，49(7):3937-3940.

［12］GE X，ZHU Z Q，REN R，et al.A novel variable reluctance resolver with nonoverlapping tooth－Coil windings［J］.IEEE Transactions on Energy Conversion，2014(99):1-11.