弹性车轮纵向力刷子模型分析

李波，赵又群，陈月乔，李小龙，臧利国

(南京航空航天大学能源与动力学院，江苏南京210016)

车轮是汽车的重要组成部件，是汽车与地面接触的唯一媒介，起到支撑负荷，向地面传递制动力、驱动力和转向力，以及缓冲减振的作用。此外，车轮具有安全性、耐久性、经济性和舒适性等要求，而安全性尤为重要。由于车轮要承受来自不良路面的磕碰以及可能遭遇穿孔、爆胎等情况，严重时甚至危及乘员安全，所以为适应现代汽车工业的发展需要，弹性车轮应运而生［1-4］。在充气车轮建模领域已经有大量的研究工作［5-9］，具体类型可以分为经验模型和物理模型。经验模型主要根据轮胎实验数据，通过函数拟合或插值方法给出研究车轮特性的公式;后者则是根据车轮与路面之间的相互作用机理和力学关系建立模型，只在模拟力或力矩产生机理和过程［10-12］。在物理模型中，车轮通常被简化为具有给定的物理特性的径向排列弹性单元体。为了让模拟更加准确，还要给出这些弹性单元体在道路表面的滑动能力，以及由于相邻单元体连接或包络的胎面引起的约束。然而，国内外对弹性车轮的研究却很少，T.B.Rhyne等分析对比了充气车轮和弹性车轮的4个主要性质，认为弹性车轮在某些方面更具有优势。

本文利用刷子模型［13］建立弹性车轮在刚性路面上驱动力方程，对比分析自由滚动和驱动状态下垂向力分布函数的变化，并深入研究了弹性梁厚度和滑移率对纵向合力的影响。

1 弹性车轮简化模型

与 Tweel类似，如图 1(a)［11，13］，本文研究的弹性车轮主要由弹性梁、刚性轮毂和轮辐组成，如图1(b)和1(c)所示。弹性梁用来代替充气车轮的内胎，起缓冲减震的作用，刚性轮毂和轮辐起到支撑作用。弹性梁由中心的弹性材料和内外两层不可伸缩的薄膜组成，这样使弹性梁具有一定的刚度。在具体分析过程中，将忽略胎面的影响，并将轮毂定义为刚性，重点分析环形弹性梁变形受力情况。

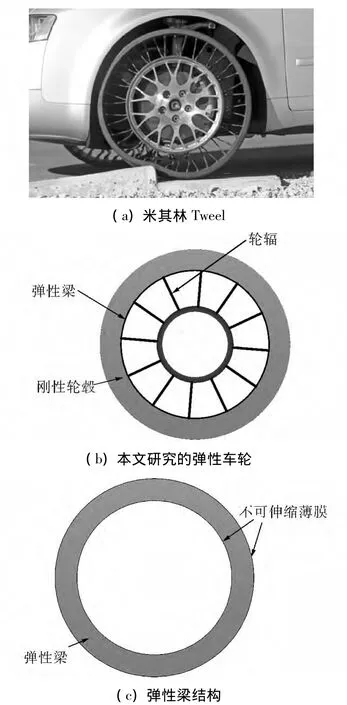
图1 米其林Tweel及本文研究弹性车轮Fig.1 Tweel and our elastic wheel

2 刷子模型构建

利用刷子模型(brush model)把结构进行简化，把弹性车轮的弹性梁看做连接在刚性基座(轮毂)上的一系列可以产生伸缩变形的弹性刷毛所组成，这些刷毛能起到承受垂向载荷以及产生车轮纵向和侧向力的作用［13］，如图2所示。在纯滚动工况下，刷毛的变形如图2(a)所示，弹性梁接地区域长为2a，由于路面摩擦力的作用，当车轮滚动速度大于车轮平移速度时，此时刷毛接地端有“粘附于路面”的趋势，从而使刷毛单元产生变形，其两端产生速度差，如图2(b)所示。

刷毛区域长2a，高度h，以刷毛单元A－A1为例，其运动形式如图3所示。相对于车轮中心，刷毛单元A点以角速度w向后转动，下端A1由于路面附着的作用，以角速度u/(r+h)向后转动。因此，刷毛在x方向的纵向变形Δx，则有:

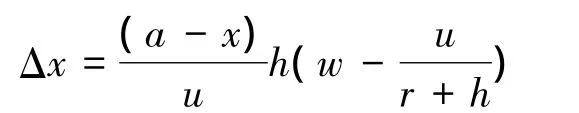
图2 基于刷子模型的车轮纵向力产生机理Fig.2 Longitudinal force mechanism based on brush model

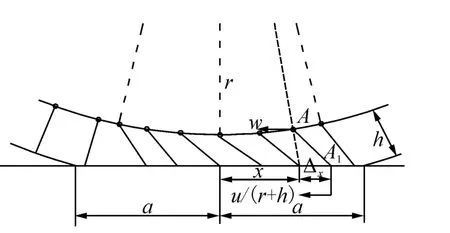
图3 刷子模型纵向受力图Fig.3 Longitudinal force diagram of brush model

假设产生正比于刷毛单元纵向形变的单元弹性力:

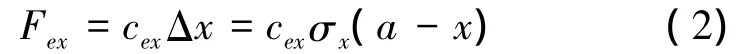
式中:cex为刷毛单元纵向刚度。

因此，整个接触区域的纵向力可以由积分得出:

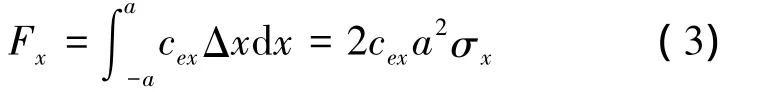
若将纵向力简化为

式中:cx=2cexa2为弹性梁纵向滑转刚度。

由式(4)看出，弹性梁纵向力与滑转率成线性正比关系，但是此模型还没有考虑达到或超过地面附着极限值时的情况，因此需要对模型进行修正。首先考虑弹性梁接地印迹内的垂向载荷分布情况，显然，在自由滚动状态(如图2(a))接地印迹中心的垂向压力最大，前后逐渐减小为零，下面根据刷子模型求解接地印迹上垂向压力分布(如图4)。在接触区x点处，以刷毛单元A－A1为例分析垂向变形Δz。根据几何关系可以求解。

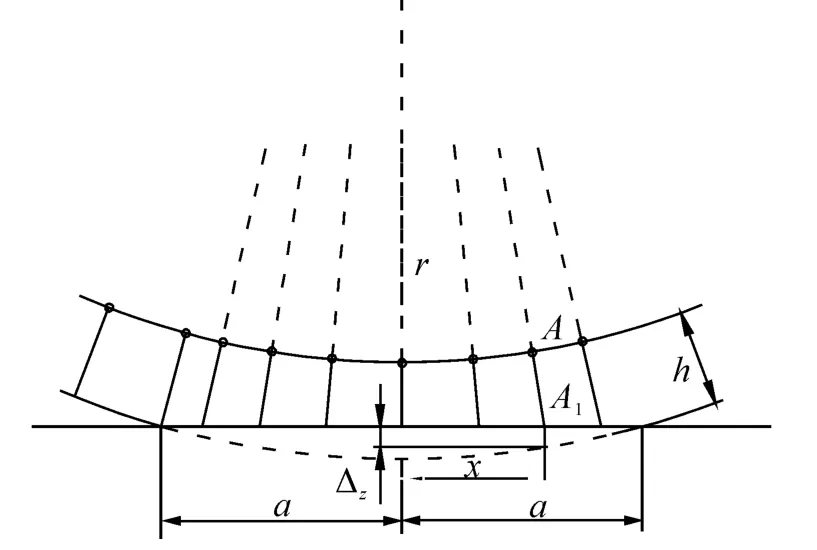
图4 刷子模型垂向受力图Fig.4 Vertical force diagram of brush model

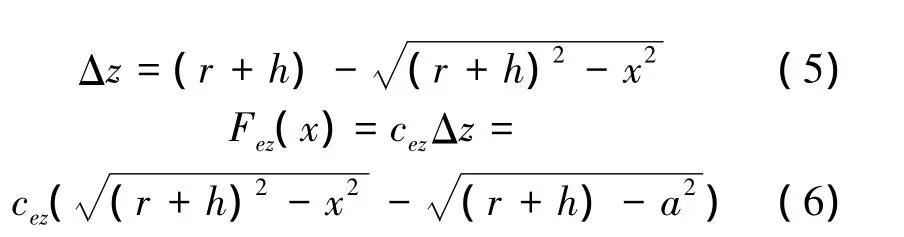
式中:cez为弹性梁垂向刚度，若垂向力Fz为已知，可由表达式求出。

若地面附着系数为μ，则每一个单元的最大纵向力有如下关系式:

弹性车轮接地区域纵向力Fex的分布如图5，可以看出，临界点xs将整个接地区域分为两部分:前部分为附着区;后部为滑移区。

图5 自由滚动状态时接地区域驱动力分布情况Fig.5 Driving force distribution in ground contact area at free rolling state

在车轮驱动时，接地印迹垂向压力最大值就会偏离中心，接地印迹上垂向压力分布就不是式(6)，而要考虑滑移率的影响。假定驱动状态接地印迹压力分布为

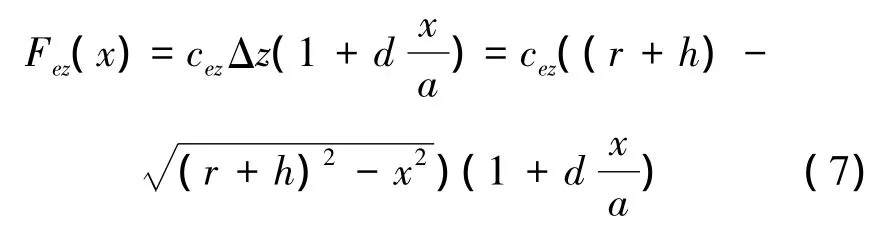
式中:d为压力分布系数，可以控制压力分布形状，决定最大压力在向左或向右移动。，否则在接触区内会出现负压力值。如图6所示，不同的d对应不同的曲线，根据实际情况选择最合适的曲线是比较困难的。实际上，压力分布会随着周围环境发生剧烈变化。

图6 不同的d对应不同的压力分布曲线Fig.6 Pressure distribution curves for different d values

关于cez的值，若载荷Fz为已知，可根据如下方程求解

同样求解xs，可以根据如下方程求解:

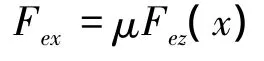
根据式(2)和(7)

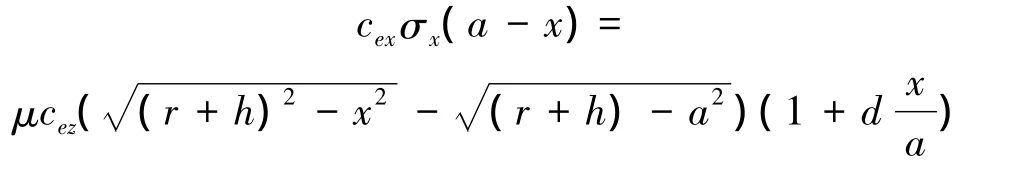
因此整个接地印迹的纵向力为两部分之和，即

车轮静摩擦系数μst要大于滑动摩擦系数μsd，所以弹性车轮滑移区纵向力应该表示为

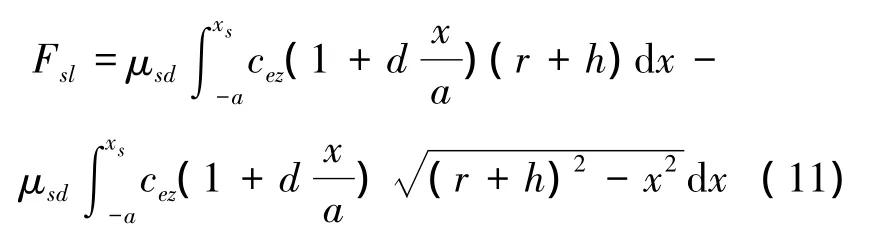
3 纵向力参数分析

如图7所示纵向力Fx与弹性梁滑转率σx之间的关系曲线。从图中当σx增大到0.3时，Fx取最大值，随后变化平稳。

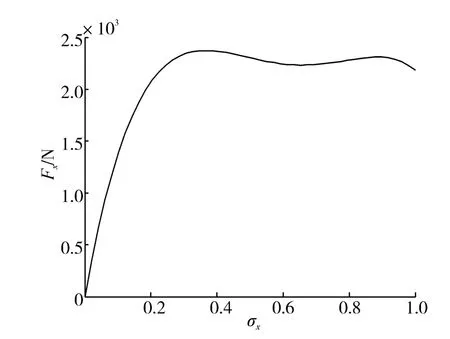
图7 纵向力Fx与弹性梁滑转率σx之间的关系曲线Fig.7 Relationship curve between longitudinal force Fxand slip rate of elastic beam σx

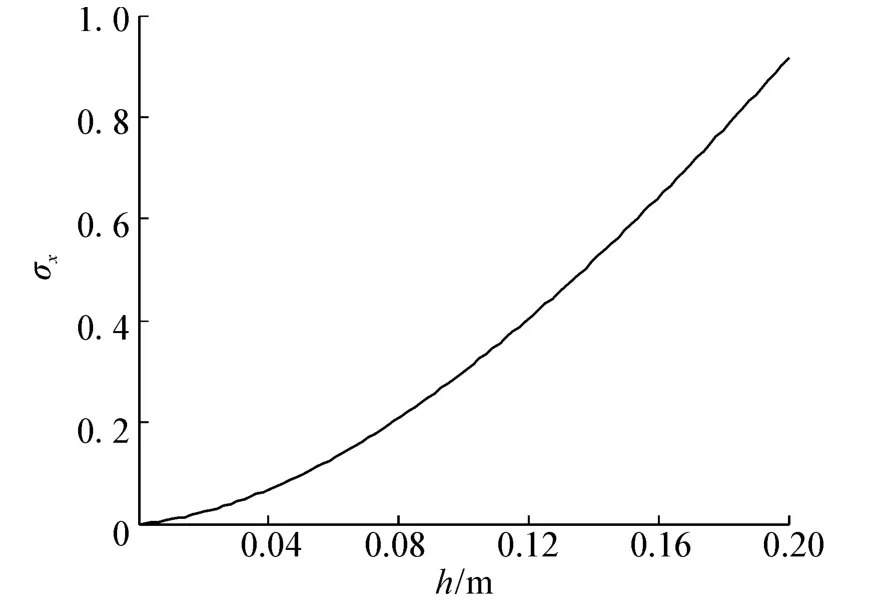
图8 弹性梁的厚度h与弹性梁滑转率σx的关系图Fig.8 Relationship curve between thickness of elastic beam h and slip rate of elastic beam σx

如图9所示，随着弹性梁的厚度h变大纵向力Fx急剧增大，直到h→0.1时，Fx取得最大值。但h增大会导致纵向刚度的减小，因为纵向力继续增大。

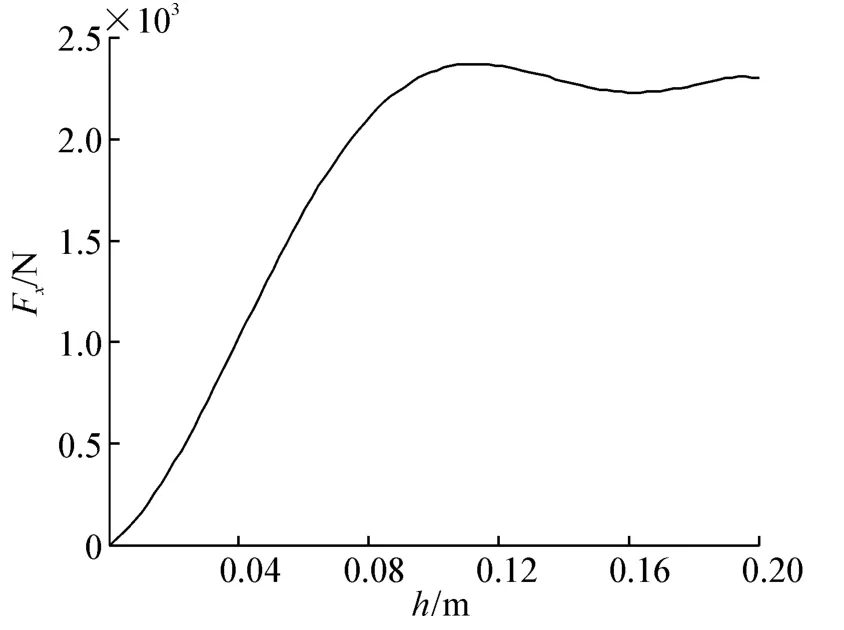
图9 弹性梁的厚度h与弹性车轮纵向力Fx的变化关系Fig.9 Relationship curve between thickness of elastic beam h and longitudinal force Fx

4 结论

在刚性路面上，将弹性车轮进行简化，给出了基于刷子模型的弹性车轮纵向力模型。根据刷毛几何变形条件和滑移理论，建立了自由滚动状态车轮接地印迹的垂向力和纵向力分布函数。根据弹性车轮的特点，建立弹性梁厚度与驱动力的关系，以及弹性梁滑移率与驱动力的关系，具体结论如下:

1)当 σx∈(0，0.3)时，弹性车轮纵向力Fx随着纵向滑移率σx的增大而增大，当σx∈(0.3，1)时，随着纵向滑移率σx的增大，Fx几乎不发生变化。

2)随着弹性梁的厚度h增大弹性梁滑转率σx增大，而且上升速率变大。

3)，随着弹性梁的厚度h变大纵向力Fx急剧增大，直到h→0.1时，Fx取得最大值。

［1］管欣，王鹏，詹军，等.金属弹性车轮的建模与动态仿真研究［J］.中国机械工程，2007，18(21):2637-2641.GUAN Xin，WANG Peng，ZHAN Jun，et al.Modeling and dynamic analysis of a metal elastic wheel［J］.China Mechanical Engineering，2007，18(21):2637-2641.

［2］岳红旭，赵又群.一种新型安全车轮的非线性有限元分析［J］.中国机械工程，2012，23(11):1380-1385.YUE Hongxu，ZHAO Youqun.Nonlinear finite element analysis of a new safety wheel［J］.China Mechanical Engineering，2012，23(11):1380-1385.

［3］汪伟，赵又群，姜成，等.新型机械弹性安全车轮的力学传递特性分析［J］.江苏大学学报，2013，34(3):261-266.WANG Wei，ZHAO Youqun，JIANG Cheng，et al.Characteristics analysis of mechanical transmission for a new mechanical elastic wheel［J］.Journal of Jiangsu University，2013，34(3):261-266.

［4］RHYNE T B，CRON S M.Development of a non-pneumatic wheel 3［J］.Tire SciTechnol，2006，34:150-169.

［5］GUO K，LIU Q.A generalized theoretical model of tire cornering properties in steady state condition［R］.(s.l.):SAE Technical Paper，1997.

［6］GUO K，LU D.UniTire:unified tire model for vehicle dynamic simulation［J］.Vehicle System Dynamics，2007，45(S1):79-99.

［7］GUO K，LU D，CHEN S，et al.The UniTire model:a nonlinear and non-steady-state tyre model for vehicle dynamics simulation［J］.Vehicle System Dynamics，2005，43(supll):341-358.

［8］PACEJKA H B，BESSELINK I J M.Magic formula tyre model with transient properties［J］.Vehicle System Dynamics:International Journal of Vehicle Mechanics and Mobility，1997，27(S1):234-249.

［9］PACEJKA H B，BAKKER E.The magic formula tyre model［J］.Vehicle System Dynamics:International Journal of Vehicle Mechanics and Mobility，1992，21(S1):1-18.

［10］SVENDENIUS J，GAFVERT M，BRUZELIUS F，et al.Experimental validation of the brush tire model 5［J］.Tire Science and Technology，2009，37(2):122-137.

［11］GAFVERT M，SVENDENIUS J.A novel semi-empirical tyre model for combined slips［J］.Vehicle System Dynamics，2005，43(5):351-384.

［12］SVENDENIUS J，GÄFVERT M.A semi-empirical dynamic tire model for combined-slip forces［J］.Vehicle System Dynamics，2006，44(2):189-208.

［13］GORDON T.Vehicle dynamics lectures notes［R］.Ann Arbor:University of Michigan，2004.