时频域滤波沉底目标亮点特征提取方法研究
2015-08-23朱广平王飞孙辉
朱广平,王飞,2,孙辉
(1.哈尔滨工程大学水声工程学院,黑龙江哈尔滨150001;2.沈阳辽海装备有限责任公司,辽宁沈阳110000)
由于水下目标回波的亮点结构能够清晰地反映出目标的物理信息(如目标的尺度及材料属性等),因此,目标亮点特征常常是主动声呐目标识别提取的重要特征之一[1]。经过多年的研究及众多科研工作者的努力,在水下复杂目标回波亮点物理[2-4]及统计特性分析[5]方面取得了较多成果。然而,目前在海洋探测中,主动声呐探测识别人造沉底目标仍是一个非常棘手的问题。这是因为沉底目标常常体型较小且静止不动,尤其是严重的海底混响干扰对目标回波的污染,导致目标回波信号的信混比较低,不能有效地提取到目标的亮点特征,大大降低了主动声呐探测识别的性能。因此,研究如何有效抑制混响干扰提取目标回波亮点特征的方法,就成为了提高主动声呐识别沉底目标性能的关键环节。由于混响干扰在时域或者频域与目标回波信号存在一定的相似性,单从时域或频域抑制混响干扰效果并不理想。近年来,基于时频分析的特征提取方法取得了较多成果,如文献[6]采用高斯窗的短时分数阶傅里叶变换提取回波中稳健的时频特征,文献[7]对目标宽带回波进行时频谱重排压制混响再进行匹配检测的方法,以及文献[8]应用希尔伯特黄变换提取混响与目标回波的希尔伯特谱特征等,文献[9]将时频分析引入到了处理收发分置声呐目标特性分析中。
为更好提取沉底目标亮点特征,将文献[10]研究工作进一步延伸,首先将时频滤波方法应用于抑制混响干扰及噪声,从而提高其信混(噪)比。在时频滤波基础上,依据LFM脉冲的目标回波信号特性,采用Hough变换及其投影方法提取沉底目标回波的亮点特征。
1 时频域滤波方法
1.1 时频滤波的基本思路
LFM(linear frequency modulation)信号具有良好的脉冲压缩性能及较强的抗干扰能力,经过拷贝相关处理后,有很好的分辨力,因此常用于测量水下目标的亮点特征。当测量沉底目标的亮点特征时,经过拷贝相关后得到的亮点特征常常淹没在较强的海底混响干扰中,严重影响目标亮点特征的正确提取以及后续对目标的正确识别。因此,如何有效地抑制混响干扰是正确提取目标亮点特征及识别的重要前提。
根据文献[10]可知,经互魏格纳变换后,目标回波信号与混响及噪声信号在时频域上能量聚集特性不同,即LFM脉冲的目标回波在时频域上能量集中分布在一条直线上,通过HT(Hough transform)变换后形成一个峰值,而混响及噪声在时频域上能量分布是杂乱的,通过HT变换后不能形成峰值。因此,基于目标及混响在时频域上不同的能量聚集特性,可以在二维时频域上进行时频滤波抑制混响及噪声,从而更好地提取亮点特征。二维平面上,由于脊波变换能很好的在脊波域表示直线特征,即在脊波域表示直线特征的脊波系数大于非直线特征的系数,因此可以类似于小波变换的阈值滤波方法,将二维时频域变换到脊波域,通过合理设置门限进行阈值滤波,滤波后再进行脊波逆变换到时频域,这样在时频域既保留了目标回波信号又滤除了混响及噪声。考虑到自适应轴向均值滤波的计算量与滤波增益,本研究中省略了时频域自适应均值脊波变换滤波中自适应轴向均值滤波步骤。
因此,时频滤波的基本思路是:对混响干扰的沉底目标回波,首先通过XWVD变换到二维时频域,依据目标回波与干扰在时频域能量聚集特性的不同,在时频域对其进行脊波变换滤波。
1.2 XWVD 变换
在上世纪末有学者提出了一种计算两个信号的互时频分布-WVD变换。
设接收信号为

式中:s(t)为发射信号,n(t)为噪声或者混响干扰。


互魏格纳变换的优点:1)接收信号x(t)与发射信号的拷贝信号s(t)作变换,充分利用了目标回波信号与发射信号的相关性,从一定程度上提高了信噪比。2)由于目标回波常常含有多个亮点,而XWVD变换可以有效避免多亮点之间的交叉项,为后续正确提取目标亮点提供了必要保证。
1.3 脊波变换滤波
脊波的定义

脊波的支撑集为f(x,ω),在脊线u·x=b垂直方向上的横截面上是小波曲线,而脊线方向上为一条直线。
连续脊波变换的定义为
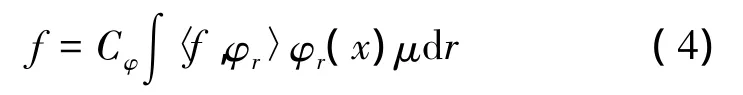
其中,φ满足容许条件,Cφ=π (2π)-d。
时频域是二维的,因此,取d=2,a0=2。则脊波函数可以变换为

式中:a是尺度,θ是角度,b是位置。这样,可以得到脊波函数的支撑集为:{(x,y)‖xcos θ+ysin θ|-b≤a}。其脊波变换系数为

其中,φ*为φ的共轭。
重构公式为

分别对连续脊波yi[(w·xi)+b]-1≥0,i=1,2,..,n中的3个参数离散化得到离散脊波:

通常 θ离散化按 θi,j=2πθ0l2-j进行离散,角度离散化的采样步长和尺度成反比。通过离散化,在数字信号处理时可进行有限离散脊波变换(finite discrete ridgelet transform,FRIT)。
LFM信号在时频域上为沿一条直线上的脊状峰,而混响及噪声在时频域上常常是较为杂乱的,由于脊波变换后在脊波域表示直线的脊波系数大于非直线特征的系数,因此可以通过阈值滤波滤除混响和噪声后再进行逆变换到时频域,这样既保留了LFM信号又滤除了混响和噪声。
脊波变换滤波方法总结如图1所示:首先对时频域信号进行离散脊波变换,即将时频域变换到脊波域,然后进行阈值滤波处理,最后进行逆变换重构时频域信号。阈值滤波中,门限可采用蒙特卡洛方法从纯噪声或混响样本中计算得到,工程中比较容易实现。

图1 脊波变换滤波方法Fig.1 The sketch of ridgelet transform filtering
2 沉底目标亮点特征提取
2.1 目标回波的亮点结构及物理含义
在主动声呐和雷达领域中,目标在某一方位的散射回波常常是由几个较强信号分量组成,对应每个分量称为一个亮点,因此,目标回波可理解为多个亮点的相互叠加。单个亮点的传递函数[4]:

式中:A(r,ω)是幅度反射因子,τ是时延,φ是回波形成时产生的相位跳变。根据以上3个参数可以完全确定亮点的特性。按照线性叠加原理,总的传递函数可以表示为
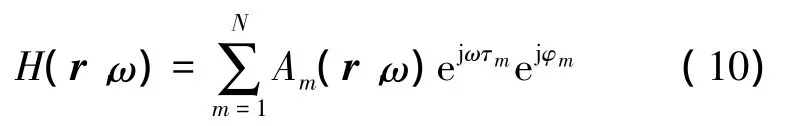
由上述亮点的概念可知,如果发射信号为s(t)(复解析形式),即一个目标时域回波信号可写为

在物理意义上,τi是第i个亮点相对于参考时间点的时延,其反映了目标的尺度信息。ai是第i个亮点的幅度,反映了目标散射点的散射强度信息。φi是相位跳变信息,ai和φi与材料属性有关。这就是沉底目标的亮点特征可作为识别的重要特征依据。在实际测量中,往往由于存在环境影响(如混响噪声、声起伏等)以及测量误差的原因,使得φi不宜测量,而τi、ai较为稳定,因此在实际工作中常常采用包含τi、ai信息所形成的向量作为特征向量。
2.2 Hough变换与亮点的关系
对时频滤波后的二维数据可采用Hough变换有效地获得在二维面上目标亮点峰。为了解二维面上目标亮点峰物理含义,有必要研究一下Hough域上的目标亮点峰与亮点模型中τi、ai的关系。
Hough变换实质是利用点与线的对应关系,将(t,ω)平面上的直线映射到 (ρ,θ)平面上的一个点,这点的能量就等于(t,ω)平面该直线上能量的积分,所以Hough变换实际上就是沿着时频平面上的直线路径积分。
Hough变换的参数化表达式为
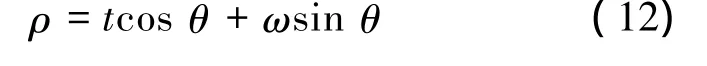
其中,ρ≥0,0≤θ≤2π ,ω=2πf。
由式(12)可知,LFM信号能量在时频面分布在一条直线上,因此Hough变换后会在(ρ,θ)平面内形成一个峰值。显而易见,该峰值的强度大小可反映出ai的大小,在此不作推导。
推导Hough变换与亮点时延特征的关系,若在ρ-θ平面上 (ρi,θi)点处出现峰值,代入式(12)有

两边同除 cosθi得

由上式可知,Hough变换是沿着斜率k=,截距的直线路径积分。

图2 目标回波中含有两个亮点的时频分布示意图Fig.2 The sketch of time-frequency distribution of target echo involving two highlights
如果目标回波中含有两个亮点,其时频示意图如图2所示,发射信号为LFM,S1、S2分别为两个亮点回波信号分量,调频斜率为k。经Hough变换后2 个峰值分别出现的位置为 (ρ1,θ1)、(ρ2,θ2),则

因为信号分量S1、S2的调制率相同,所以斜率k相同,也即θ1=θ2=θ0,在实际中θ0可由发射信号LFM脉冲信号频率调制斜率k确定,θ0=arctank。
当ω=0时,得到两信号分量的关于时间轴上的:截距
若设t=0时刻为参考时间点,则亮点时延:

式中:Δ=ω0tanθ=ω0k,ω0为LFM初始频率。式(17)、(18)为Hough变换与亮点τi的位置对应关系。2个亮点间的时间延迟差为

由此可见,亮点模型中的亮点间的时间延迟差正比于在ρ-θ平面上ρ1-ρ2值,而 cosθ0可由发射信号事先确定。这就是Hough变换与亮点模型时间延迟参数重要的关系。可见在实际工程中,只需对ρ-θ平面上向ρ轴作投影计算,即可得到目标的亮点结构的特征向量。
2.3 沉底目标亮点特征提取步骤
基于时频域滤波的沉底目标亮点特征提取步骤为:
1)将接收到的目标回波信号与发射信号的拷贝信号作XWVD变换,得到二维的时频域信号;
2)进行时频滤波,即对时频域信号作脊波变换,进行阈值去噪后作脊波逆变换,得到滤波后的时频域信号;
3)将滤波后的输出进行Hough变换,时频域中的回波亮点分量变为Hough平面内的波峰;
4)对Hough平面内的杂波进行阈值滤波;
5)将去噪后的信号投影到ρ轴上,得到提取出的一维特征向量。

图3 基于时频滤波Hough变换的目标特征提取流程图Fig.3 The sketch of extraction features of target based on time-frequency domain filtering and Hough transform
3 支持向量机
在主动目标识别问题中,实际采集得到的样本数目可能较少,由于支持向量分类器具有对小样本数的适应性以及很高的泛化性,因此将采用支持向量机作为整个目标识别系统的分类器。支持向量机就是求取最优分类面问题,而最优分类面问题可以转化成下面的带有约束条件的优化问题,即在约束条件yi[(w·xi)+b]-1 ≥ 0(i=1,2,..,n)下,求式(20)的最小值。

由Lagrange极值理论可得到支持向量机判别函数为

关于支持向量机的详细推导请见文献[14]。
沉底目标识别过程可分为2步:1)对采集的样本进行时频域滤波及Hough变换提取沉底目标亮点特征:2)训练支持向量机,训练后即可投入实际应用。在本研究中,将采用支持向量机对常规拷贝相关提取沉底目标亮点特征与本特征提取方法作统计对比研究。
4 仿真及实际实验研究
4.1 仿真实验
采用仿真方法产生了具有2个亮点的目标回波及白噪声干扰。发射信号为LFM脉冲信号,带宽为20 kHz,脉冲宽度为 2.5 ms,信号的采样频率为200 kHz。将目标回波信号和噪声叠加形成接收信号,仿真出的信号如图4所示。

图4 仿真产生的目标信号和接收信号Fig.4 Target signal and receive signal in terms of simulation
分别对信噪比为-5 dB和-20 dB的接收信号作XWVD脊波变换滤波,时频滤波结果如图5、6所示。当SNR=-5 dB时,将接收信号与拷贝信号作XWVD变换到时频域后,可清晰地观察到目标回波两个分量,再经过脊波变换滤波滤出了大部分噪声,凸现了目标回波的两根亮线。当SNR=-20 dB时,将接收信号与拷贝信号作XWVD变换到时频域后,由于信噪比较低噪声干扰也较为严重,再经过脊波变换滤波后抑制了大量噪声。
再将经过滤波的时频图分别作Hough变换及门限滤波,并向ρ轴投影提取亮点特征向量,结果如图7所示。经过Hough变换及阈值滤波后,通过提取峰值,进一步抑制了噪声干扰,因此可以提取到较好的亮点特征(如图7)。
为了突出本文提取方法的有效性,采用拷贝相关处理方法作比较,也分别对SNR=-5 dB和SNR=-20 dB的数据进行处理,提取出的亮点结果如图8所示。比较图8与图7可知,在较低的信噪比下(SNR=-20 dB),通过时频滤波方法及Hough变换可以提取到清晰的亮点峰值。而常用的拷贝相关处理方法在较低的信噪比下提取到的亮点特征很不明显。注意,图7中的两亮点间距与图8不同是因为
图7中的横轴为ρ轴,没有乘以(详见 2.2节)。通过对仿真实验数据的处理结果比较可知,基于时频滤波Hough变换的目标亮点特征提取方法是有效果的。

图5 SNR=-5 dB时噪声中时频滤波实验结果Fig.5 The results of time-frequency domain filtering in noise(SNR=-5 dB)


图6 SNR=-20 dB时噪声中时频滤波实验结果Fig.6 The result of time-frequency domain filtering in noise(SNR=-20 dB)
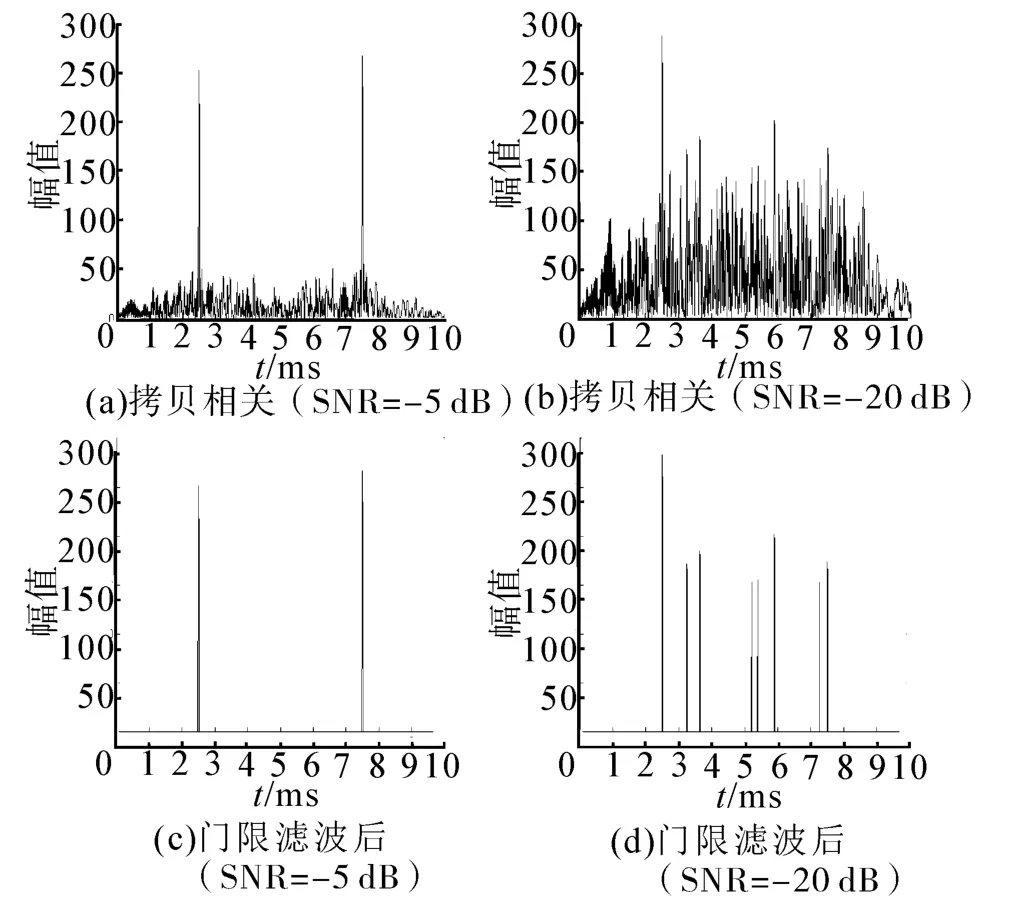
图8 拷贝相关提取的目标特征Fig.8 The features of target using copy-correlation
4.2 水池实验
实验水池底部铺敷厚度为50 cm的细沙,水深为72 cm。收发合置换能器经连接杆固定在一平台下。目标模型为一面球冠状一面平面的圆柱壳体,模型以一定姿态沉于沙层之上,目标的上端系一圆盘以调节目标方位角度。信号源产生LFM信号,有效带宽80 kHz,脉宽为0.05 ms。由于发射换能器束宽的限制,测量时采用了较小的掠射角,得到的数据信混比较高。为了突出时频滤波方法优势,又专门采集了大量的纯混响数据,然后与目标回波数据相叠加,形成较低信混比的接收数据用于比较本方法与拷贝相关处理方法的处理效果。

图9 时频滤波实验实例处理结果Fig.9 The example of filtering in time-frequency domain

图10 Hough变换及阈值滤波后的结果Fig.10 The results of Hough transform and filtering
图9是对一组实验数据进行XWVD及时频滤波处理的结果。图10为对其时频滤波结果进行Hough变换及门限滤波后的结果。图11(a)是时频滤波Hough变换投影后提取到的特征向量,而图11(b)为对接收整个数据进行拷贝相关处理的结果,在目标区域为 0.4~0.5 ms,但其淹没在混响之中,无法正确提取亮点特征。比较结果可知,基于拷贝相关得到的目标特征已经被混响淹没,而基于时频滤波的目标特征相对比较突出。

图11 两种方法提取出的目标特征的比较Fig.11 The comparison of extracted features between new method and copy-correlation method
4.3 特征提取效果的统计识别研究
为了进一步验证本文提取沉底目标亮点特征方法的性能,进行了基于支持向量机为分类器的统计识别研究。实验数据来源为:实验采集了各个角度的目标回波222组数据。此外,采集了大量的纯混响数据。将含有2个亮点的数据截取出来,与对应长度的混响叠加起来形成目标回波信号,通过调整混响幅值的大小改变信混比。
从实验数据中提取出的目标特征向量(共222组数据)中抽取一半的数据用于支持向量机的训练,剩余一半的实验数据作为待识别样本。实验中真目标为提取的目标特征向量,假目标为纯混响数据(共222组数据)。
当信混比分别为12、5及0 dB时,分别采用基于时频滤波的目标特征提取方法以及拷贝相关处理方法提取特征,并用支持向量机进行训练然后识别,得到的识别率如表1所示。

表1 2种亮点特征提取方法识别性能的比较Table 1 The comparison of recognition performance between two methods of extracting highlights
由表可知,在较高信混比下,两种特征提取方法对真假目标均能较好识别,随着信混(噪)比的降低,支持向量机对2种方法提取特征的识别率均有下降,然而采用时频滤波提取特征的方法的识别率较高,如SNR=5 dB时,采用时频滤波提取特征的真假目标的识别率为20.7%和78.1%,而拷贝相关提取特征的真假目标的识别率为8.6%和51.5%,相比分别高出12.1%和26.6%。由此可见,在本实验数据条件下,通过时频域滤波Hough变换后投影提取沉底目标亮点特征的方法更能有效地滤除混响干扰与噪声,从而提高沉底目标的识别性能。
5 结论
研究了时频域滤波Hough变换提取沉底目标回波亮点特征方法,该方法的特点是:
1)接收信号x(t)与发射信号的拷贝信号s(t)作XWVD变换,利用了目标回波与发射信号的相关性抑制了部分混响及噪声,在时频平面提高了信混(噪)比。并且XWVD变换避免多亮点之间的交叉项,为后续正确提取目标亮点提供了必要保证。
2)经过XWVD变换到时频域后,利用目标回波信号与混响及噪声信号的时频域上能量聚集特性不同,在时频域上进行脊波变换滤波进一步抑制混响干扰及噪声。
3)研究了Hough变换域中的峰值位置与目标亮点模型对应的数学关系。利用Hough变换提取目标回波中各亮点峰,并进行投影计算形成目标回波的亮点特征。
通过实验研究,并与拷贝相关提取亮点特征方法进行了比较,结果表明:通过时频域滤波Hough变换后能有效的抑制混响干扰及噪声,更好地提取到了沉底目标的亮点特征,提高了对沉底目标回波的识别性能。
[1]李秀坤,李婷婷,夏峙.水下目标特性特征提取及其融合[J].哈尔滨工程大学学报,2010,31(7):903-908.LI Xiukun,LI Tingting,XIA Zhi.Feature extraction and fusion based on the characteristics of underwater targets[J].Journal of Harbin Engineering University,2010,31(7):903-908.
[2]汤渭霖.声呐目标回波的亮点模型[J].声学学报,1994,3(19):92-100.TANG Weilin.Highlight model of echoes from sonar targets[J].Acta Acustica,1994,3(19):92-100.
[3]范军,朱蓓丽,汤渭霖.非刚性表面声呐目标回波的修正几何亮点模型[J].声学学报,2001,26(6):545-550.FAN Jun,ZHU Beili,TANG Weilin.Modified geometrical highlight model of echoes from nonrigid surface sonar target[J].Acta Acustica,2001,26(6):545-550.
[4]BUCARO J A,HOUSTON B H,SANIGA M,et al.Broadband acoustic scattering measurements of underwater unexploded ordnance(UXO)[J].J Acoust Soc Am,2008,123(2):738-746.
[5]陈云飞,李桂娟,王振山,等.水中目标回波亮点统计特征研究[J].物理学报,2013,62(8):284-294.CHEN Yunfei,LI Guijuan,WANG Zhengshan,et al.Statistical feature of underwater target echo highlight[J].ACTA Phys Sin,2013,62(8):284-294.
[6]王强,潘翔.水下沉底小目标回波的短时FrFT滤波分析[J].浙江大学学报:工学版,2008,42(6):918-922.WANG Qiang,PAN Xiang.Analysis of small underwater bottomed target echo time-frequency filter characteristics based on short-time FrFT[J].Journal of Zhejiang University Engineering:Science,2008,42(6):918-922.
[7]王强,潘翔.面向沉底目标的分数阶傅里叶变换谱重排回波时频处理[J].中南大学学报:自然科学版,2009,40(6):1649-1654.WANG Qiang,PAN Xiang.Bottom object echo time-frequency processing based on two dimension fractional Fourier transform reassignment spectrogram[J].Journal of Central South University:Science and Technology,2009,40(6):1649-1654.
[8]李秀坤,谢磊,秦宇.应用希尔伯特黄变换的水下目标特征提取[J].哈尔滨工程大学学报,2009,30(5):542-546.LI Xiukun,XIE Lei,QIN Yu.Underwater target feature extraction using Hilbert-Huang transform[J].Journal of Harbin Engineering University,2009,30(5):542-546.
[9]SHAUN D A,KARIM G S.Time-frequency analysis of the bistatic acoustic scattering from a spherical elastic shell[J].J Acoust Soc Am,2012,131(1):164-173.
[10]朱广平,孙辉,朱凤芹.时频域自适应均值脊波变换滤波及检测方法[J].哈尔滨工程大学学报,2010,31(9):1172-1178.ZHU Guangping,SUN Hui,ZHU Fengqin.Detecting signals using adaptive mean and ridgelet transform filtering in a time-frequency domain[J].Journal of Harbin Engineering University,2010,31(9):1172-1178.
[11]CANDES E J.Ridgelet theory and applications[D].Standford:Standford University,1998:23-38.
[12]HELBERT D.3-D discrete analytical ridgelet transform[J].IEEE Transactions on Image Procesing,2006,15(12):3701-3714.
[13]BARBAROSSA S.Analysis of multicomponent LFM signals byacombined Wigner 2 Hough transform[J].IEEE Transactions on Signal Procrssing,1995,43(6):1511-1515.
[14]瓦普尼克.统计学习理论[M].中国:电子工业出版社,2004:293-420.
