船厂钢板堆场多时段作业计划优化

张志英，王维泽，侯俊

(同济大学机械与能源工程学院，上海200092)

在船舶制造中，钢板堆场是连接外部物流和内部物流的枢纽，承担着生产所需钢板的进料、保管和供应职责，是实现精益造船的重要环节，具有以下特点:1)尺寸约束，即同一堆垛中，相邻的两块板尺寸之差不能超过约束值，否则会引起上层板的形变;2)时间约束，每块钢板都有固定的入库时间与出库时间;3)从多时间段角度，堆场管理属于多阶段决策优化问题，从垛位分配角度，属于组合优化问题;4)每批次入库和出库钢板数量多，入库时需要考虑对已入库和后入库板的影响，垛位分配难度大，属于NP-Hard问题。因此，钢板堆场调度难度大，目前国内外学者对造船厂钢板堆场问题研究主要有仿真方法和智能算法两类。仿真方法的主要目的实施现堆场管理自动化。蒋如宏等在分析堆场系统结构特征及堆放规则的基础上，应用数据库和计算机仿真技术建立堆场数字化仿真模型［1］;C.Park等用仿真方法研究了堆放场地大小、堆垛计划日期变化等因素对堆场管理的影响［2］。随着遗传算法等智能算法的广泛运用，金淳等以出库作业时间最短为目标研究出库作业，并运用遗传算法求解模型［3］;刘建峰等结合堆场库存现状及钢板出入库计划，采用遗传算法研究入库钢板的分配策略［4］;徐萍等采用遗传模拟退火算法研究了造船厂的钢板入库作业［5］。以上研究将入库和出库分开，且应用智能算法求解，运行时间长，只适合解小规模问题。因此，Zhang等建立出库和入库的综合模型，采用贪婪算法实现快速求解［6］，但忽略了堆场倒垛主要是由不同时间段的入库出库板相互叠压引起的。因此，在上述研究的基础上，建立了一个以减少倒垛量为目标的多时间段钢板堆场优化模型;提出由动态规划启发式算法和变邻域搜索算法组成的两阶段求解算法，并利用实际生产中的数据验证其有效性与实用性。

1 问题描述和数学模型

1.1 船厂钢板管理过程和问题描述

钢板管理包括钢板预算、钢板采购、供货、钢板存放、进出库计划、切割计划和余料管理等。文中主要研究钢板入库、在库管理和出库等过程的计划安排与优化问题。

1.1.1 钢板入库出库计划

入库计划的目的是为一批到货钢板安排合理垛位。理想情况下，先出库钢板应该放在上层以减少倒垛量，而实际作业中，每个到达批次包含不同出库日期的钢板，先出库钢板会被后入库后出库的钢板叠压，引起倒垛。因此钢板入库堆放时不仅要结合当前库内钢板的堆放情况，同时要考虑与后期入库、出库作业的相互影响。出库计划主要根据后道工序的切割计划编制。为了保证后道工序的顺利进行，钢板必须按时按量在规定的时间节点出库，而且也不能提前出库，否则会造成切割钢板的大量积压和丢失。

1.1.2 钢板的在库管理

图1所示的钢板堆场由4个跨组成，每跨包含18个堆垛，在跨内部和跨之间钢板分别通过桥吊和传送带搬运。堆场的每一跨内部主要有3个区域组成:卸货堆垛、临时堆放堆垛和上料堆垛。各跨预留马路两侧的堆垛作为卸货堆垛，在卸货堆垛内可以调整入库顺序;为了平衡传送带的负荷，同时又不影响桥吊的工作效率，在传送带附近设置一些上料堆垛;堆场中余下的堆垛作为临时堆放堆垛。

图1 钢板堆场结构示意图Fig.1 Structure of steel plate stockyard

在堆场中钢板首先被卸载在卸货堆垛，待临时堆放堆垛中需要出库的钢板全部搬运至上料堆垛后，再将卸货堆垛中的钢板运至临时堆放堆垛中合适的垛位。因此堆场作业计划优化的研究对象是由钢板从卸货堆垛进入临时堆放堆垛的入库作业，钢板离开临时堆放堆垛的出库作业，以及相关的倒垛作业组成。

1.2 数学模型

假设:

1)每天为一个时间段，多个时间段为一个计划期;2)计划期开始前和结束时堆场为空;3)钢板到达时间段和离开时间段已知;4)为了减少倒垛量，堆场在某个时间段内作业顺序为先出库，后入库;5)每个时间段出库和入库的钢板批次都不会超过一个;6)每个时间段内入库钢板数量不会超过堆场容量;7)跨之间不能倒垛。

根据以上假设，针对入库、出库及倒垛作业，整个堆场可以表示为如图2所示的独立作业单元，堆场由S个堆垛构成，S=m×n，堆垛位置表示为(x，y)。

图2 堆场模型Fig.2 Stockyard model

堆垛中的钢板的层计数方式为从上到下，为了方便堆场管理描述，设置如下符号:T为计划期长度;t为第t个时间段;、分别表示t时间段钢板出库后和入库后堆垛(i，j)中的钢板数量;为堆垛(i，j)的第k层钢板;、分别表示t时间段内钢板出库后和入库后的堆场{1，2，..，m，j=1，2，3，..，n，k=1，2，..，}，{|i=1，2，..，m，j=1，2，3，..，n，k=1，2，..，};vt为t时段入库钢板总数;为t时间段的序号为g的入库钢板;πt为t时间段入库钢板集合，πt={|，g=1，2，..，vt};Π 为计划期内的入库钢板集合，Π={πt|t=1，2，..，T};num为每块入库的板唯一的标识;Zt为t时间段出库钢板的数量；为第t第z块出库钢板，∈;ut为t时间段的出库钢板集合，ut={1，2，..，m，j=1，2，..，n，z=;1，2，..，Zt};Ω 为计划期内出库集合，Ω={ut|t=1，2，..，T}。

模型参数和变量如下:

H为每个垛位中可堆放的钢板数量的上限;Q为一个无限大的值;ψ为异类板集合;At为第t时间段出库需要倒垛的钢板集合;δw为同一个堆垛中，两块相邻钢板之间的宽度差极限δl为同一个堆垛中，两块相邻钢板之间的长度差极限。

决策变量:

因此，目标函数为

除特殊说明，否则qijz∈ut∈ πt，i=1，2，..，m，j=1，2，..，n，i＇=1，2，..，m，j＇=1，2，..，n，t=1，2，..，T。式(6)～(9)中w∈e，w＇∈e＇，e∈，e＇∈。

其中，式(1)为目标函数，最小化计划期内各个时间段内倒垛量的总和;约束(2)保证t时间段内一块入库钢板只被分配到一个位置上;约束(3)保证t时间段内每个位置只放一块钢板;约束(4)保证t时间段内一次倒垛发生，钢板只被放到一个新位置;约束(5)保证t时间段内钢板不被悬空放置;约束(6)和(7)表示同一个堆中两块相邻钢板间的宽度差异限制;约束(8)和(9)表示同一个堆中的两块相邻钢板的长度差异限制。

2 两阶段优化求解方法

定义:异类板，指在堆场管理中引起倒垛的板，包括两类:一种是受尺寸约束，入库时需要倒垛的板;另一种是出库时引发倒垛的板。

船厂钢板堆场多时段作业计划优化既是一个多阶段优化决策问题，又是一个组合优化问题。根据多时段堆场性质，将问题划分为两个阶段求解，首先针对多阶段性，采用动态规划启发式算法得到初始解及异类板集合，然后从组合优化出发采用变邻域搜索算法对初始解进行组合优化。

2.1 阶段I－动态规划启发式算法

船厂钢板堆场多时段作业计划优化属于多阶段最优决策问题，即不论当前状态是由以前何种决策所造成，余下的策略对当前的状态，必定构成最优策略［7］。

多时段作业的每个时间段是一个相对独立的单元，按时间段的先后顺序将研究的问题划分为T阶段，第t阶段对应第t时间段，x(t)对应第t时间段出库结束时的状态，u(t)(t=0，1，..，T－1)代表第t时间段的出库、入库和倒垛决策，则问题表示如下:

x(t+1)=Ht(x(t)，u(t))，Ht代表状态转移函数，令F为总目标函数，ft为第t阶段的目标函数，递归函数如下:

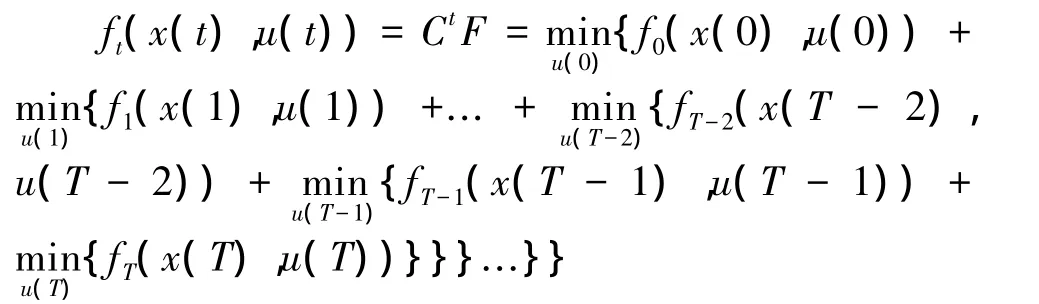
为了减少运算时间，在决策阶段引入启发式规则，如动态规划启发式算法步骤2)所示。动态规划的实施过程如图3所示，根据动态规划递归函数的终止条件，在T阶段出库结束后的空堆场基础上，将T阶段出库的钢板ut按启发式规则分配垛位，状态转移得到，即第T－1阶段钢板入库后的堆场，将第T－1阶段入库的钢板πT－1移除，获得，同理取得各阶段堆场中的堆放状态。

图3 动态规划启发式算法示意图Fig.3 Dynamic programming based heuristics

动态规划启发式算法步骤如下:

1)令t=T，转2);

2)ut在的基础上入库，获得:

①从ut随机选出板，从ut中删除，转②;

②在的堆场状态下，令i=1，j=1，k=1，(x，y，z)为插入的位置，ftemp为相应的倒垛量，Stemp表示目标位置与的长之差与宽之差之和，令x=0，y=0，z=0，ftemp=Q，Stemp=Q，转③;

③如果zijt≥H，则转⑨;如果，则转⑤;如果与满足约束(7)－(10)，则转④，否则令k=k+1，重复③;

④如果存在，k＇=k，k+1，..，，的入库日期与的入库日期相同，则引起的倒垛量temp1=0;否则，令k＇=k－ 1，转⑤;

⑤比较与的入库日期，如果＇先入库，则temp1=temp1+2;如果k＇≠ 1，则令k＇=k＇－1，重复⑤;如果k＇=1，则转⑥;

⑥如果ftemp＞temp1，则转⑧;如果ftemp=temp1，则转⑦;如果ftemp＜temp1，则转⑨;

⑦用temp2表示与的长之差和宽之差的和，如果Stemp＞temp2，则转⑧，否则转⑨;

⑧更新相应的入库候选位置信息:

x=i，y=j，z=k，ftemp=temp1，Stemp=temp2，转⑨;

⑨如果i＜m，令i=i+1，转③;否则转⑩;

⑩如果j＜n，令j=j+1，转③;否则

3)利用 πt－1通过得到:删除中所有第t－1阶段入库的钢板，同时更新堆垛信息，获得，如果t＞1，则t=t－1，转2);否则结束循环。

2.2 阶段Ⅱ－变邻域搜索算法

目前，邻域搜索算法已广泛运用于集装箱堆场和钢厂堆场调度中，包括集装箱出库［8］、集装箱出库预处理［9］和钢厂钢板倒垛［10］。在船厂钢板堆场多时段作业计划优化中以异类板为中心构造邻域，消除异类板的同时可能产生新的异类板，因此邻域结构需要变换。Hansen等提出的变邻域搜索算法在大规模组合优化问题有突出的表现［11］，适合船厂钢板堆场，其优良性由两个关键步骤决定:局部搜索和邻域结构改变。通过局部搜索可以在一个邻域内找到局部最优解，在局部最优解的基础上改变邻域结构以跳出局部最优达到全局最优。

Nk(k=1，..，+∞)表示邻域结构集，Bk表示相应的局部最优解，Ek表示局部最优解产生的倒垛次数，ψ表示每一个领域结构对应的异类板的集合，νk表示第k块异类板的邻域，νk［j］表示第j个可行解，是一个垛位编号，如(x，y，z)，νk∈Nk，Gk记录第k个局部最优解时，计划期内每个时间段堆场的所有堆垛中z最大的异类板集合，α是结束搜索系数，指的是从第m个邻域结构出发，如果在第(m+α)个邻域结构时还找不到更优的解，则结束搜索，Eα为最优解。

变邻域搜索算法步骤如下:

1)统计出库入库引起的倒垛量:

①t=1，转②;

②遍历Ot2-1中所有堆垛，统计每个堆垛出库时间段为t的钢板数量l，及所有出库板所在层位置z的最大值zmax，temp=temp+2×(zmax－l)，如果zmax≠1，则Gk=Gk+numzmax;遍历结束后转③;

③遍历Ot2中所有堆垛，统计入库时间段为t的钢板数量l，及所有入库板所在层位置z的最大值zmax，temp=temp+2×(zmax－l)，如果zmax≠1，则Gk=Gk+numzmax，如果t≥T，则结束，否则t=t+1，转②。

2)K邻域的构造及搜索:

①k=1，执行 1)，Ek=temp，转 ②;

②从Gk中随机选择一张板numk，且numk∉ψ，构键νk:t为入库时间遍历找出所有(x，y，z)，且numk与rxyz，及rxy(z－1)与numk满足约束(7)－(10)νk=νk+(x，y，z)，转③;

③执行1)，在Bk的基础上计算numk入库位置为vk［i］时的temp，如果temp＜Ek，则Ek=temp，Bk更新为最新堆场垛位信息，遍历vk，转④;

④如果k＞α ，且Ek－α＜Ek－α+1，Ek－α+2，..，Ek，则结束搜索;否则令k=k+1，转②;

3 实例验证与数值分析

3.1 实例验证

为了验证所提方法的实用性和有效性，下面将两阶段方法与文献［1］的仿真和文献［4］的遗传算法(GA)进行比较。

3.1.1 算例设置

算法是在Windows 7系统上基于Visual C#实现，选取某大型船厂的实际数据验证，研究的计划期T=4，堆场有12个堆垛，即S=12，每一桩位最高堆叠层数H=20，变邻域搜索算法中的结束搜索系数α=5。GA的参数选取为:种群规模N=500，进化代数M=200，交叉概率=0.95，变异概率=0.05。

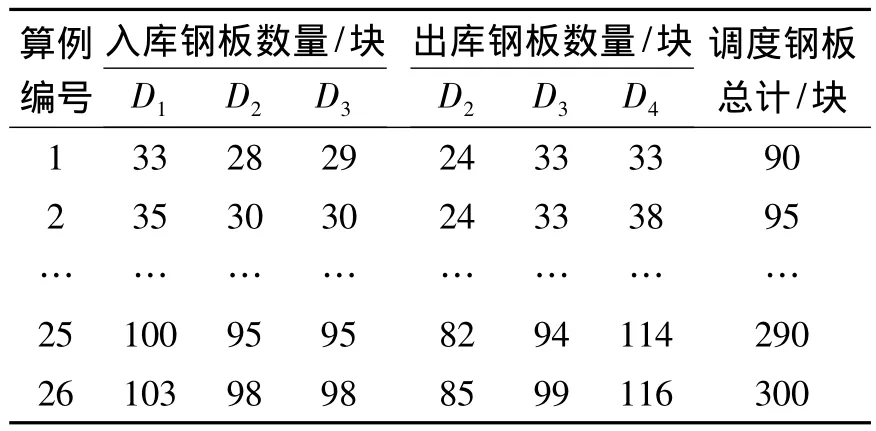
表1 实例数据Table 1 Actual data

根据参与调度的钢板数量的不同设置了26组算例(如表1)，表中Dn代表第n天。得到3种途径下的倒垛次数R1，R2，R3和运行时间，如表2所示，α12和α13表示两阶段方法比另外两种方法的倒垛次数优化率，α12=(R2－R1)/R2，α13=(R3－R1)/R3，负值表示没有起到优化作用。

3.1.2 实验结论及结果分析

表2为实例验证结果。图4为3种方法倒垛量与钢板数量关系图。对结果进行分析，可知:1)如图4，当GA参数固定时，在某个钢板数量范围内求得较优解。当参与调度的钢板数量少于125张时，遗传算法优于两阶段方法;当参与调度的钢板数量较多，大于130张时，两阶段方法优于遗传算法，倒垛次数减少6%至75%。2)仿真方法在小规模问题时优于两阶段法。当钢板量大时，解的质量下降，此时使用两阶段方法倒垛量可以减少28%至75%。3)遗传算法运行时间长，并且随着钢板数量增加，运行时间快速增长，当钢板数量为300张时，运行时间已经达到 4 897.7s。

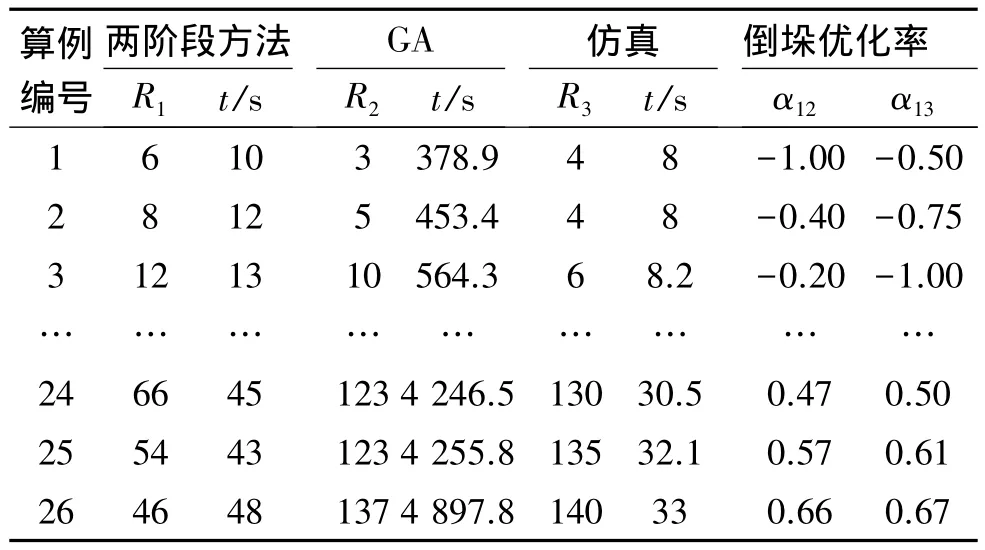
表2 算例结果Table 2 Output of numerical experiment

出现以上结果的原因是仿真方法依靠人工决策规则，对大量钢板出入库时难以适应;而遗传算法容易陷入局部最优化。如果要兼顾全局性，需要针对不同的钢板数量范围，调整种群规模、遗传代数、交叉概率及变异概率，从而增加算法使用复杂程度和运算时间。相比较，本文的两阶段方法在解决实际生产中的大规模钢板出入库调度问题时运行时间短，结果优异。

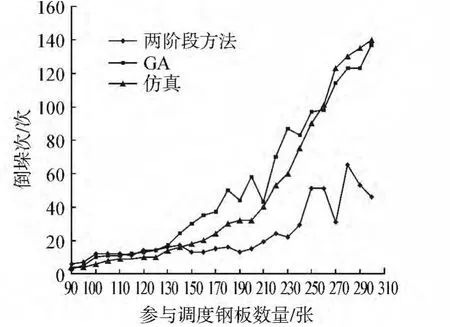
图4 倒垛量与钢板数量的关系图Fig.4 Shuffling operation quantities vs steel plate quantities

3.2 数值试验与讨论

在一个计划期内，钢板堆场的倒垛量与两阶段方法的参数α值选取有密切关系。

以表1中第26组算例为对象，研究α值对结果的影响。如表3所示，其中t表示运行时间，k表示邻域结构的数量，可以看出α增加，倒垛次数减少，运行时间变长，原因是由于α越大，VNS越容易逃逸出局部最优，搜索的范围越广，全局性越好，运行时间也增加。理论上，只要α足够大，可以找到最优解。

以α=7为例分析最优解与α的关系，以邻域结构编号为横坐标，局部最优解为纵坐标，作邻域结构变化图，如图5所示:1)总体上倒垛量不断减少;2)在相邻的几个邻域结构容易陷入局部最优化，比如第1，2…，6邻域结构时，假如当α=1或2就无法逃逸出该局部最优陷阱，最优解等于邻域结构N3的局部最优解，不能继续搜寻到N18时的局部最优解。

表3 α与R、t、k的关系Table 3 The relationship between α and R ，t，k

图5 局部最优解随邻域结构的变化情况Fig.5 The diagram of local optimum and neighborhood structure

4 结束语

不同钢板在不同时间段入出库是引起堆场倒垛的主要原因，本文综合考虑一个计划期内的钢板出库、入库问题，建立了以减少倒垛量为目标的钢板堆场多时间段堆场作业计划优化模型，并把问题分解为两个阶段求解，使复杂问题简单、易实现。两阶段方法由动态规划启发式算法和变邻域搜索算法构成，最后运用实例，与遗传算法和仿真结果作对比，证明了本文所提出的两阶段方法的实用性和有效性，同时通过数值实验，研究了算法参数对结果的影响。

［1］蒋如宏，钟宏才，谭家华.船厂钢板堆场管理的数字化仿真［J］.上海交通大学学报，2003，37(7):1242-1245.JIANG Ruhong，ZHONG Hongcai，TAN Jiahua.Simulation of digitized plate stockyard management in shipyards［J］.Journal of Shanghai Jiaotong University，2003，37(7):1242-1245.

［2］PARK C，PARK J C，BYEON G G，et al.Steel stock management on the stockyard operations in shipbuilding:a case of Hyundai Heavy Industries［J］.Production Planning and Control:The Management of Operations，2006，17(1):1-12.

［3］金淳，王广民，高鹏.造船厂钢板出库作业计划的建模及优化研究［J］.工业工程与管理，2009，14(6):12-17.JIN Chun，WANG Guangmin，GAO Peng.Modeling and optimization on operation scheduling for a steel plate yard in a shipyard［J］.Industrial Engineering and Management，2009，14(6):12-17.

［4］刘晓峰，张小辉，蒋志勇，等.基于遗传算法入库钢板分配策略［J］.江苏科技大学学报:自然科学版，2011，25(6):524-529.LIU Xiaofeng，ZHANG Xiaohui，JIANG Zhiyong，et al.Allocation strategy of steel plate in store house based on genetic algorithm［J］.Journal of Jiangsu University of Science and Technology:Natural science Edition，2011，25(6):524-529.

［5］徐萍，葛世伦.造船厂钢板入库作业优化研究［J］.航海工程，2012，41(1):33-37.XU Ping，GE Shilun.Optimization on entering storage operations of steel plate in a shipyard［J］.Ship and Ocean Engineering，2012，41(1):33-37.

［6］ZHANG Zhiying，WANG Peng，WANG Weize.Optimization and operation scheduling for a steel plate yard based on greedy algorithm［J］.Journal of Networks，2013，8(7):1654-1659.

［7］李瑞，钱富才，李力，等.动态规划问题研究［J］.系统工程理论与实践，2007，8:56-64.LI Duan，QIAN Fucai，LI Li，et al.Research on dynamic programming［J］.Systems Engineering theory and Practice，2007，8:56-64.

［8］LEE Y，LEE Y.A heuristic for retrieving containers from a yard［J］.Computer and Operation Research，2010，37(6):1139-1147.

［9］LEE Y，CHAO Shiliang.A neighborhood search heuristic for pre-marshaling export containers［J］.European Journal of Operational Research，2009，196(2):468-475.

［10］王敏，李铁克，王伯琳.多对多板坯倒垛问题的一种邻域搜索算法［J］.计算机集成制造系统，2010，16(3):658-671.WANG Min，LI Tieke，WANG Bailin.Local search algorithm for the overlapped turned-out slab pile problem［J］.Computer Integrated Manufacturing Systems，2010，16(3):658-475.

［11］MLADENOVIC N，HANSEN P.Variable neighborhood search［J］.Computer and Operations Research，1997，24(11):1097-1100.