欠驱动AUV自适应编队控制策略

黄海，张强，张树迪，万磊，庞永杰

(哈尔滨工程大学水下机器人技术重点实验室船舶工程学院，黑龙江哈尔滨150001)

自主式水下机器人(autonomous underwater vehicles，AUVs)在军事上可广泛应用于水域侦查、中继通讯、区域探雷、智能攻击等。在民用方面，可用于海底生物资源探查，矿产资源采样，海底地形勘测，沉物打捞，地震地热活动监测，海洋环境监测等［1］。编队控制可以更好的利用AUV的传感器系统实现海洋环境的协作探测和作业［2-3］。近年来，人们针对AUV的编队控制进行了深入的研究，并提出了许多控制方法，例如V.Djapic等基于机器人智能提出了行为控制的编队方法［4-5］，西北工业大学基于领航员-跟随法［6］使用前馈加反馈控制器研究了多 AUV 的主从编队控制［7］，Z.H.Ismail提出使用人工势场法［8-9］保持多AUV编队的几何形状等。而由于AUV的欠驱动特性，它的队形保持通常需要基于模型的的非线性路径跟踪控制方法作为基础［10-11］。E.Yang等针对多个非完整的链式AUV的领航员－跟随者编队保持，提出了非线性的时变光滑反馈控制律［12］。Saing Paul Hou等提出了考虑AUV的动力学模型，提出自适应比例和微分控制器用于多AUV的编队控制［13］。在异构AUV的编队中，通常采用领航员－跟随者编队形式来实现编队控制。在这种方法中，通常是由领航员跟踪一个预定义的路径，而跟随AUV将与领航员保持期望的几何构型［2，14］。考虑到AUV的欠驱动特性，本文将基于人工势场原理定义多AUV编队的期望区域，建立自适应编队控制策略跟踪预定轨迹，并保持编队的几何构型。

1 自适应编队策略

1.1 坐标系的建立

在多AUV的编队中，对每个AUV在其中心点上建立局部坐标系(xi，yi，zi)和绝对坐标系(x0，y0，z0)。对于第i个AUV，如果不考虑横摇，运动学模型可以用下面的等式表示:

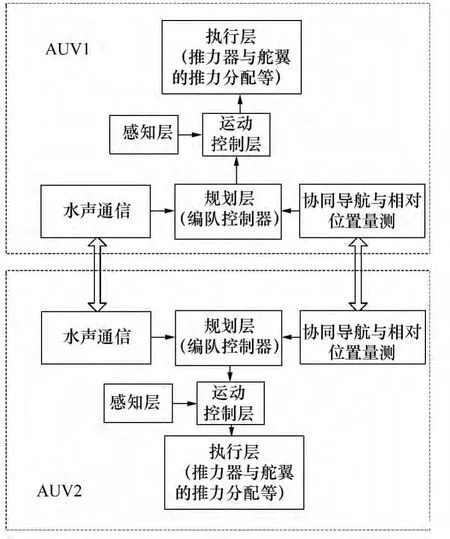
图1 欠驱动AUV编队的系统结构Fig.1 Control architecture for under-actuated AUVs formation

但由于欠驱动AUV和其他类型的水下航行器相比有较大的差别，它主要通过一个主推螺旋桨辅以舵翼的运动实现AUV的前进、下潜和转艏，其基础控制内容主要包括速度控制、艏向控制和下潜深度控制(由AUV前进的同时纵倾控制实现)，而轨迹控制也是综合上述3种控制所得到的结果。

根据文献［15］的单个AUV运动控制，本文建立了欠驱动AUV控制系统结构。如图1所示，单个AUV的控制体系结构包括感知层、运动控制层和执行层。多AUV编队控制器作为规划层，通常是在运动控制层的上层向单个AUV发送期望速度、期望角度和期望下潜深度指令，再由单个AUV的基础控制加以完成。

所以本文将根据AUV的欠驱动特性建立基于柱坐标系的运动学模型，使自适应编队控制器所得到的AUV期望区域或期望点更为直观地表达为单个AUV的期望速度、期望角度和期望下潜深度，以有利于编队规划层指令的发送。

1.2 势函数的建立

势场法是机器人编队控制常用的方法。势场函数的梯度可以帮助多机器人系统调整其控制输入，使它们沿着梯度方向移动，并最终稳定在势能函数的局部极小值(期望点)。但对于AUV的编队控制复杂系统，需要设定特定的期望区域，以利用区域控制策略［16］实现编队控制。

根据AUV在柱坐标系的运动学方程，设第i个AUV qi的期望区域是以期望形心为圆心，半径介于R1、R2之间，高度为h的环状区域，其中，

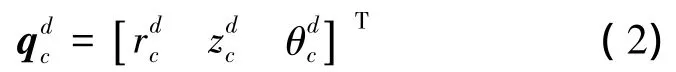
是期望编队区域的中心。因此，期望编队区域可以定义为如下的不等式:

式中:δ qiok=qi－，是第k个期望区域的恒定参考矢量点，k=1、2、3;θh是允许的艏向角误差;fSk(δ qiok)是具有连续偏导数的标量函数。

在约束条件(2)、(3)的描述下，期望编队区域的势能函数定义为

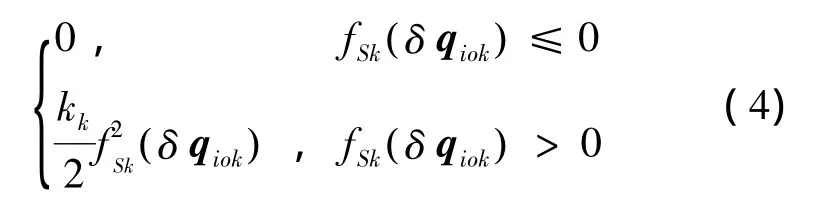
因此对式(4)的势能函数微分，则第i个AUV与期望区域的势能函数偏差定义为

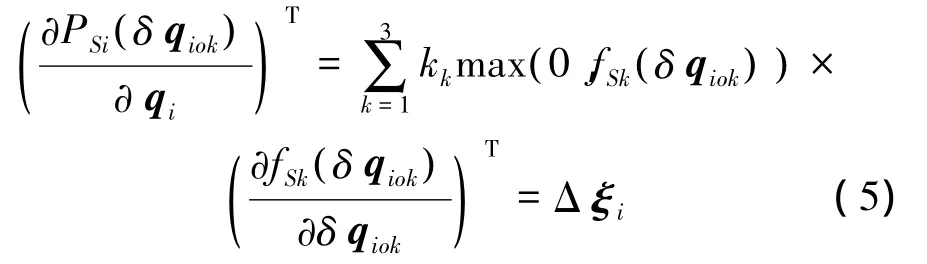
可见，当AUV在期望区域外时，势函数对AUV产生引力。

为了在编队中保证AUV之间的距离，使AUV之间的距离越近，势函数所产生的斥力越大，还定义了AUV的分层避碰区域。其中避碰函数为

式中:δ qij=qi－qj;g1ij、g2ij、…、gLij分别为避碰势函数第1层，第2层和第L层(最内层)，并且这些层次连续可微，r1、r2、rL分别表示第一层，第二层和最内层的半径。

避碰势能函数定义为

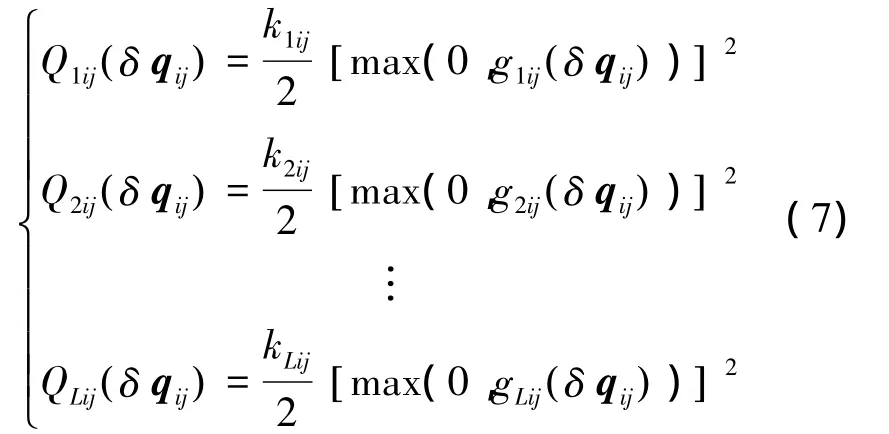
式中:kLij＞…＞k2ij＞k1ij，并且都是正常数。第i个和第j个AUV之间的避碰势能为

对式(8)的势能函数微分，得到第i个AUV在避碰区域内势能偏差为

因此，如果设定式(2)为AUV编队的期望中心，则AUV的期望位置，编队形状和避障区域都可以通过方程(3)～(6)定义。

1.3 自适应编队控制器

第i个AUV动力学方程可表示为

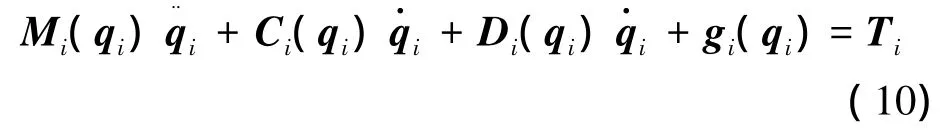
式中:Mi(qi)是AUV的6×6质量和惯量阵，矢量是 6×6 的离心加速度和科氏加速度矩阵，Di(qi)是阻尼矩阵，gi(qi)是重力加速度矢量，Ti包含推力器推力和舵翼的力矩。

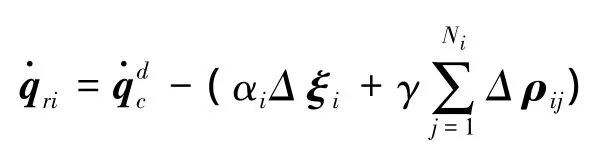
式中:αi和γ是正常数。并设定

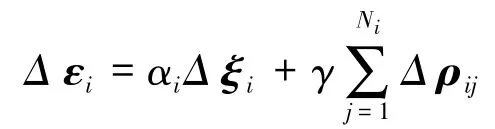
定义第i个AUV的滑动面为

微分方程(11)对于时间的表达式为

将式(11)、(12)代入式(10)，得到:

根据自适应控制原理，式(13)可表示为［16］

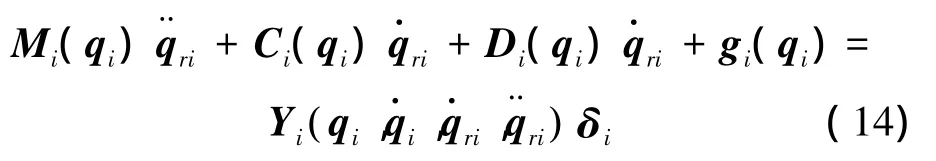
式中:Ksi和Kp为控制器的可调控制参数，Ksi和Kp为正定阵。在控制中通过调整Ksi和Kp的值，确定AUV编队中期望编队区域和避碰区域的权重。估计参数被更新为:

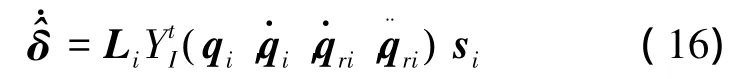
式中:Li是正定阵。如果把式 (15)代入式 (13)，则得到系统控制的闭环动力学方程:

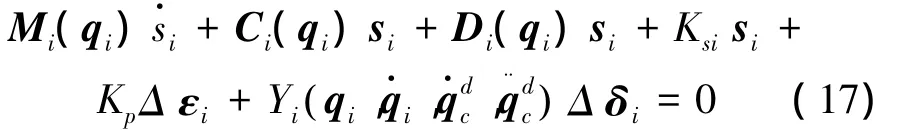
式中:Δ δi=δi－。

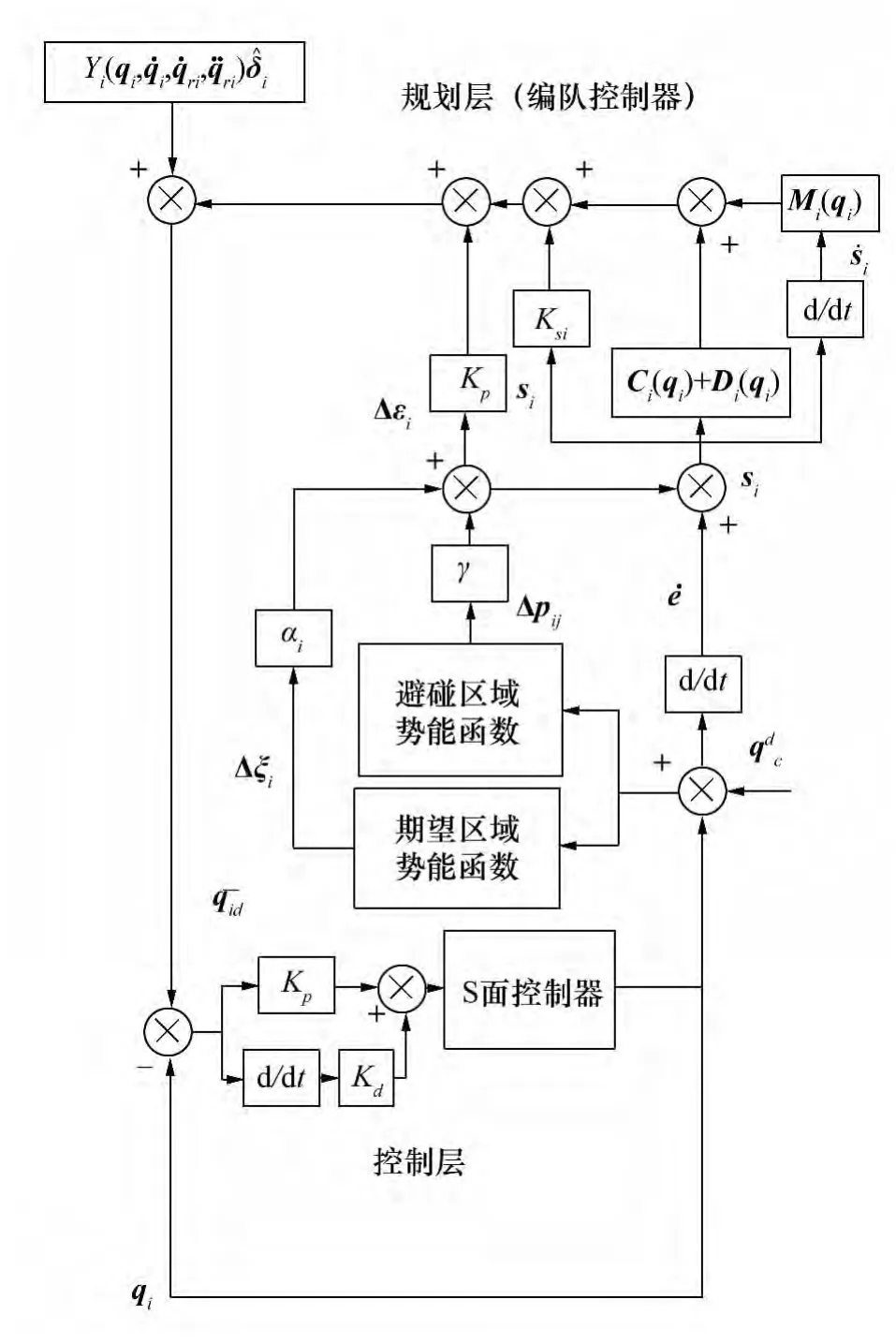
图2 自适应编队控制器框图Fig.2 Diagram of adaptive formation controller

由图2，自适应编队控制器建立在控制层上层，主要通过建立和调整避碰区域和期望区域的权重规划出适合欠驱动AUV的轨迹。所以为了证明编队控制器的稳定性，定义和期望区域、避碰区域及闭环控制相关的二次型函数之和作为多AUV系统的李亚普诺夫函数:

2 仿真结果

为了验证前面所提到的自适应编队控制策略，本文通过串联3个欠驱动AUV的控制平台和操纵性仿真平台，搭建了自适应编队控制的仿真平台。其中AUV的控制平台采用文献［17］的S面控制方法，经过推力分配分别控制AUV的主推螺旋桨、舵、翼实现速度、艏向和深度控制。AUV的操纵性仿真平台基于潜水器的六自由度动力学方程，动力学方程中包含水动力试验获得的AUV水动力系数，输入AUV主推螺旋桨的控制电压、舵翼的控制角度，通过推力电压曲线将主推螺旋桨换算为螺旋桨推力，输出为AUV实时位置。编队的期望路径由仿真平台进行规划，编队过程中各AUV位置由AUV之间的通信进行传递，并通过仿真平台计算AUV之间的距离，为每个AUV发送期望速度、艏向和深度信息。AUV主要在静水的仿真环境中完成编队，由于并未设定障碍物，系统的干扰源主要来自不同AUV之间的相互干扰。

图3 欠驱动AUV到达期望区域Fig.3 Under-actuated AUV arriving at desired formation region

AUV的欠驱动特性和一般的机器人不同，其转艏和下潜是在前进中完成的，AUV并不能直接完成原地转艏和下潜，这些都给多AUV的协同编队造成了一定的困难。在图3中3个AUV的初始位置分别为(0，0，0)，(40，40，0)和(60，60，0)，AUV 的初始方向为东向，期望编队为下潜6 m，转艏90°后沿北向前进的一段直线。由于AUV是欠驱动的所以其下潜和转艏均需要AUV同时前进配合完成，AUV在转艏和下潜的同时还要完成编队，即AUV之间相对位置的改变和保持。欠驱动AUV下潜和转艏都是通过舵翼来完成的，没有办法实现垂直下潜或侧移，需要一定的速度和回转半径。所以为了在实验中充分体现欠驱动AUV编队同时转艏和下潜这一耦合运动的特点，只对AUV给出了一个中间目标点和一个最终目标点，分别为柱坐标系下和，AUV之间的相对距离由初始的AUV1与AUV2之间的56 m，AUV1与AUV3之间的84 m变为25 m的等腰三角形，其编队过程是一个期望目标点和相对距离都存在较大突变的多耦合调整过程，而势函数场力为距离误差的平方数量级，虽然可以减小误差但也造成了AUV2在跟随时由于斥力过大造成的一定的波动。而AUV2的波动反而会对AUV1和AUV3产生引力，进而产生AUV之间的相互干扰作用，造成AUV3稳定后的波动，但也正是自适应编队控制器的作用，让AUV3的波动迅速消除了。所以要经过一段调整才使3个AUV之间的相对距离误差达到稳定和期望状态。

图4 欠驱动编队跟踪空间折线Fig.4 Under-actuated AUV formation tracking 3D folding line

图5 欠驱动编队跟踪空间曲线Fig.5 Under-actuated AUV formation tracking 3D curve

在图4和图5中，3个AUV从同样的初始位置分别跟踪空间折线和螺旋线。在跟踪的过程中，其初始位置并不是理想的编队位置。AUV1(领航AUV)在仿真开始时，所受到的其他AUV的引力大于目标路径的引力，所以它尽可能地保持自己的位置，等待其他AUV和自己靠近，同时AUV2和AUV3受到AUV1的引力，将尽快趋近期望编队区域，当所受到其他AUV的引力与目标路径的引力平衡时AUV1从起始点开始跟踪路径，并在跟踪的过程中其他两个AUV进一步趋近AUV1，经过一段时间的相对速度和艏向调整，通过队形中的引力和斥力作用，到达理想的编队位置，并在空间曲线跟踪中使AUV之间的相对距离误差逐渐趋于零并保持稳定，从而完成了编队控制和相对位置保持。

3 结束语

本文根据AUV的欠驱动特性，使用柱坐标系建立了AUV的运动学模型和多AUV的期望编队区域。提出并证明了自适应编队控制策略，通过人工势场能函数，使领航员AUV完成了预定轨迹的路径跟随，同时实现了跟随中多AUV的编队和队形保持。通过建立3个欠驱动AUV编队的仿真平台，分析了欠驱动AUV在编队过程的特点，完成了空间折线和螺旋线的跟踪和编队，并使AUV之间的相对距离误差逐渐趋于零并保持稳定，证明了编队控制策略，对欠驱动AUV的编队研究具有重要的意义。

［1］CUI Rongxin，GE Shuzhi，VOON H B ，et al.Leader-follower formation control of underactuated autonomous underwater vehicles［J］.Ocean Engineering，2010，37:1491-1502.

［2］YANG Huizhen，ZHANG Fumin.Geometric formation control for autonomous underwater vehicles［C］//2010 IEEE International Conference on Robotics and Automation Anchorage Convention District，Anchorage，USA，2010:4288-4293.

［3］仲宇，顾国昌，张汝波.一种新的水下机器人集群路径规划方法［J］.哈尔滨工程大学学报，2003，24(2):166-169.ZHONG Yu，GU Guochang，ZHANG Rubo.New way of path planning for underwater vehicle group［J］.Journal of Harbin Engineering University，2003，24(2):166-169.

［4］DJAPIC V.Unifying behavior based control design and hybrid stability theory for AUV application［D］.Riversider:U-niversity of California，2009:72-105.

［5］JIANG Dapeng，PANG Yongjie，QIN Zaibai.Coordinated control of multiple autonomous underwater vehicle system［C］//Proceedings of 2010 8th World Congress on Intelligent Control and Automation.Jinan，China，2010:4901-4906.

［6］崔海英，石秀华，崔荣鑫.自主水下航行器主从式编队控制［J］.鱼雷技术，2007，15(4):42-44.CUI Haiying，SHI Xiuhua，CUI Rongxin.Leader-follower formation control of autonomous underwater vehicles［J］.Torpedo Technology，2007，15(4):42-44.

［7］贾秋玲，李广文，闫建国.水下编队航行机器人的前馈加反馈控制器设计［J］.兵工学报，2007，28(8):1008-1010.JIA Qiuling，LI Guangwen，YAN Jianguo.Feedforword/feedback controller for formation control of multiple autonomous underwater vehicles［J］.Acta Armamentarii，2007，28(8):1008-1010.

［8］ISMAIL Z H，DUNNIGAN M W.A region boundary-based geometric formation control scheme for multiple autonomous underwater vehicles［C］//International Conference on Electrical，Control and Computer Engineering.Pahang，Malaysia，2011:491-496.

［9］GU Dongbing，WANG Zongyao.Leader-follower flocking:algorithms and experiments［J］.IEEE Transactions on Control Systems Technology，2009，17:1211-1219.

［10］WOOLSLEY C A，TECHY L.Cross-track control of a slender，underactuated AUV using potential shaping nonlinear oscillations［J］.Ocean Engineering，2009，36:82-91.

［11］LAPIERRE L，SOETANTO D.Nonlinear path-following control of an AUV［J］.Ocean Engineering，2007，34:1734-1744.

［12］YANG Erfu，GU Dongbing.Nonlinear formation-keeping and mooring control of multiple autonomous underwater vehicles［J］.IEEE/ASME Transactions on Mechatronics，2007，12:164-178.

［13］HOU S P，CHEAH C C.Can a simple control scheme work for a formation control of multiple autonomous underwater vehicles［J］.IEEE Transactions on Control Systems Technology，2011，17:1090-1100.

［14］CUI Rongxin，SAM S G，HOW B V E，et al.Leader-follower formation control of underactuated AUVs with leader position measurement［C］//2009 IEEE International Conference on Robotics and Automation.Kobe，Japan，2009:979-984.

［15］甘永.水下机器人运动控制系统体系结构的研究［D］.哈尔滨:哈尔滨工程大学.2007:10-18.GAN Yong.Research on motion control system architecture of underwater vehicle［D］.Harbin:Harbin Engineering University，2007:10-18.

［16］CHEAH C C，HOU S P，SLOTINE J J E.Region-based shape control for a swarm of robots［J］.Automatica，2009，45:2406-2411.

［17］刘建成，于华南，徐玉如.水下机器人改进的S面控制方法［J］.哈尔滨工程大学学报，2002，23(1):33-36.LIU Jiancheng，YU Huanan，XU Yuru.Improved S plane control algorithm for underwater vehicles［J］.Journal of Harbin Engineering University，2002，23(1):33-36.