运用衍生工具管理我国商业银行利率风险的效率研究

王晋忠　高　菲

运用衍生工具管理我国商业银行利率风险的效率研究

王晋忠高菲

随着我国期货市场的发展及利率市场化的不断完善，如何有效利用利率衍生工具对商业银行的利率风险进行管理已成为各商业银行关注的重点。根据样本数据特征，选择运用久期、最小方差模型、VAR模型、动态的MGARCH-BEKK模型、国债期货矩阵最小方差模型以及同时运用国债期货和利率互换的矩阵最小方差模型的套期保值方法，确定最优套期保值比率，可以实证研究其效果，分析优劣。经比较，动态套期保值模型和同时运用国债期货和利率互换的最小方差模型的利率风险管理效果较好。

利率期货；套期保值；商业银行利率风险管理

DOI：10.14086/j.cnki.wujss.2015.06.008

一、研究目的及意义

利率风险是企业所面临的重要风险之一。近年来，随着利率市场化的深入和我国宏观经济的不确定性增加，伴随着高杠杆特征的利率波动，企业面临的利率风险日益增大，尤其是对利率敏感的商业银行其利率风险更受关注。自1996年利率市场化改革启动以来，我国利率市场化按照渐进式的改革路径，已先后实现了货币市场、债券市场和外币市场利率的市场化。存款保险制度的推出，预示着人民币商业银行存贷款利率市场化将可能在短期内实现。面对近年来金融市场利率波动频繁、波动幅度增大的环境，商业银行由于自身经营业务的特点，即使小幅的利率变动都可能带来重大损失，因此利率风险不容忽视。

在未推出国债期货之前，我国商业银行主要采用资产负债表管理、利率敏感性缺口管理等方法管理利率风险。国债期货的推出丰富了我国的金融衍生产品市场，也为我国商业银行提供了利率风险管理的有效手段和方法。相对于传统利率风险管理方法，运用利率衍生工具管理利率风险更具有主动性和灵活性，能显著提高利率风险管理效率。利率期货是在交易所内交易的标准化合约，具有流动性好、信用风险低、占用资金少、交易成本低等诸多优点。利率期货按照标的债券期限的不同可分为短期利率期货和长期利率期货两大类，目前我国正在交易的5年期和10年期国债期货均属于长期利率期货。

国债期货合约标的资产的期限较长，一般在5年以上，利用国债期货可有效管理商业银行所面临的长期利率风险。而我国商业银行所面临的短期利率风险也较大，需要运用其他金融工具进行管理。并且，目前我国国债期货市场刚开始运行，市场活跃度较低，产品结构不齐全，定价合理性有待提升。所以，在当前市场状况下，仅使用国债期货来管理商业银行利率风险的效果可能并不好，需要综合运用其他场外衍生金融工具。当前，中国香港、美国等地的商业银行，在管理利率风险时通常同时运用利率期货、利率互换等工具，所以我国商业银行也可以考虑同时考虑运用多种工具。在我国已有的场外交易利率衍生工具中，利率互换发展很快，已成为常用的债务保值和资本升值的有效手段之一。目前我国部分机构投资者暂时还不能参与国债期货交易，利率互换更成为各金融机构利率风险管理的主要工具。

由于无法获得商业银行所有资产负债的具体信息，对其所面临的利率风险进行具体测度，笔者借鉴海外利率风险测量的研究思想，将商业银行的股票视为一种债券，利用商业银行股票市场收益率信息，研究运用利率衍生工具对其进行利率风险管理。股票价格是市场对于企业未来价值的预期，利率的变动对商业银行资产负债的影响可以通过股票市场价格的变动反映出来。因此，笔者基于商业银行股票市场信息，考虑运用国债期货、利率互换两种工具对商业银行整理面临的利率风险进行管理。同时，由于在不同市场状态和经济条件下，衍生工具对利率风险管理的效果存在差异，笔者将对各种方法的风险管理效果进行比较，寻找在我国市场条件下适合我国商业银行的最优的套期保值方法。

二、文献综述

利用利率期货对利率风险进行套期保值的方法有很多，Ederington（1979）首先研究了运用一种利率期货合约对冲债券现货的利率风险的套期保值方法，基于使现货和期货组合方差最小化的原理，得到了确定最优套期保值比率的方法，并对美国GNMA期货和国债期货的套期保值效果进行了研究。该方法的主要不足是在套期保值过程中，作者仅从组合的方差最小化的角度，未考虑收益的变动。Franckle&Senchack（1982）在Ederington的基础上提出了最小化现货市场预期风险的套期保值模型。该模型考虑到投资者对市场未来利率的预期，对未来利率的不同预期方法会影响到套期保值的效果，但究竟如何选择利率的预期方法作者并未讨论。Kolb等人（1981）提出了基于久期的思想运用利率期货合约对债券现货进行套期保值的方法。根据债券期货和现货组合久期为0思想，计算出为了消除利率风险所需要的期货合约份数。然后，Daigler&Copper（1998）研究了利率期货对固定收益证券的久期—凸性套期保值方法，模拟结果表明无论对于利率期限结构的简单或者复杂变化，久期—凸性套期保值方法的利率风险管理效果明显优于久期套期保值方法。此后，Rendleman（1999）对利率期货进行套期保值方法中的期货久期和利率价格进行了准确的定义和修正，并且通过实证研究表明期货与现货间的期限错配可能会降低10%或者更多的风险管理效率。

由于最小方差法的最大缺点是存在残差自相关问题，于是Herbst等（1989）和Myers等（1989）提出运用双变量向量自回归模型（B-VAR）来消除残差自相关。此外，最小方差法存在的另一个重要问题就是利用期货价格与现货价格之间的协整关系，Ghosh（1993）首先研究建立了误差修正模型（ECM），同时考虑了现货和期货价格的非平稳性、长期均衡关系以及短期动态关系。Lien（1996）的研究为协整关系如何影响最佳套期保值比率提供了理论支持，他指出套期保值者如果忽视协整关系，那么他将得到一个相对较低的最小风险套期保值比率，同时套期保值效果也会相应地变差。此后，我国学者王骏等人（2005、2006）分别实证研究了VAR模型和ECM模型在我国农产品期货和金属期货上的套期保值效果。

随着对市场利率期限结构研究的深入，研究发现不同期限的利率的波动率不同，Carcano（1997）提出了波动率调整的利率风险套期保值模型，且实证结果表明波动率调整的久期、凸性和因子分析的套期保值模型的套期保值效果有显著改进。Cecchetti（1986）利用自回归条件异方差模型（ARCH）研究了美国国债期货的套期保值效果，实证结果表明最优套期保值比率随时间的改变而呈现出相当大的变化，传统的静态不变套期保值比率的假设与实践运用较为不符，需要进行适度改进，将其动态化。Baillie& Myers（1991）首先提出了运用广义自回归条件异方差模型（GARCH）来计算商品期货最优套期保值比率的思想，经实证研究表明该动态最优套期保值方法要比静态套期保值方法的效果要好，也证明了动态套期保值的优点。我国学者佟孟华（2011）和蒋彧（2013）分别研究了沪深300股指期货动态套期保值比率模型估计及比较，结果表明动态的GARCH模型具有更好的套期保值效果。

三、研究方法

笔者基于商业银行进行利率风险管理的多种方法，提出本文测度套期保值效果的方法。

（一）套期保值方法

国内外经典的套期保值方法可分为：理论弹性角度（即久期—凸性类方法）、最小方差角度、收益率角度（即期货现货收益率回归）、时间序列统计分析角度（即VAR和ECM类方法）和动态套期保值角度五类。由于传统套期保值方法的基本思想都是基于：买多少份期货可对现货头寸所面临的利率风险进行对冲。但在实际运用中，投资者往往持有不止一种债券，很可能是一个债券组合，而可用于对冲利率风险的利率衍生工具也不止一种。根据投资组合情况，可以选择多种利率衍生工具，提高利率风险管理效率。因此，Hilliard（1984）基于最小方差的基本思想研究了运用一个期货组合对冲现货组合利率风险的方法。下面就笔者实证研究中所采用的最小方差模型、MGARCH-BEKK模型和矩阵最小方差模型进行详细介绍。

1.最小方差模型

最小方差套期保值方法的主要思想是使得所持有的债券现货和利率期货组合的整体价值方差最小。通过计算组合的收益方差最小的一阶条件为0得到最佳套期保值比率，具体计算方法如下：

假定：ΔS表示现货价格变动，ΔF表示期货价格变动，h为最优套期保值比率，则现货与期货组合的收益可表示为：

此时，套期保值组合价值变化的方差为：

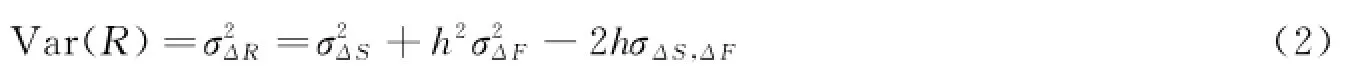
要是组合的收益率方差最小，由一阶条件等于0得：

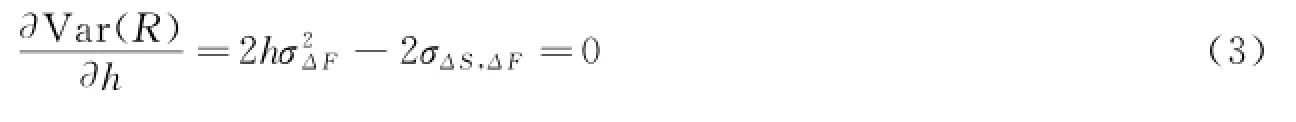
则：

最小方差法是除久期以外的另一种基本的套期保值方法，是其他套期保值方法思想的基础，且应用时基本没有限制条件。因此，笔者将选用该方法进行实证研究。

2.MGARCH-BEKK模型

在研究最优套期保值比率的文献中，许多学者的研究证明，不管是相对于静态还是其他动态套期保值模型，MGARCH-BEKK模型都具有一定的优越性。因此，笔者的实证研究部分中也将运用MGARCH-BEKK模型来估计最优动态套期保值比率。若期货和现货收益率序列不满足MGARCHBEKK模型，则不能采用此套期保值方法。

MGARCH-BEKK（1，1，K）模型的具体形式如下：εt|Ωt-1服从N（0，Ht）的分布，

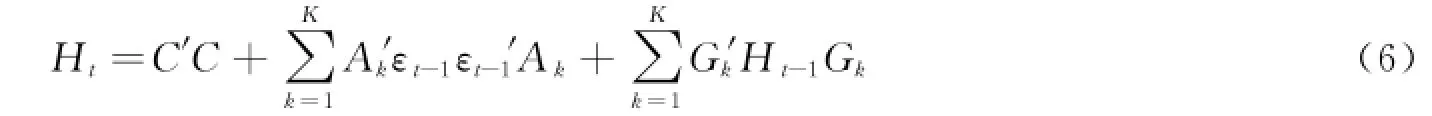
其中rt=（rs，t，rf，t）′是期货和现货收益率的组成向量，C为2×2的上三角矩阵，A和G为2×2的参数矩阵。

在K=1情况下，Ht可以展开成如下形式：

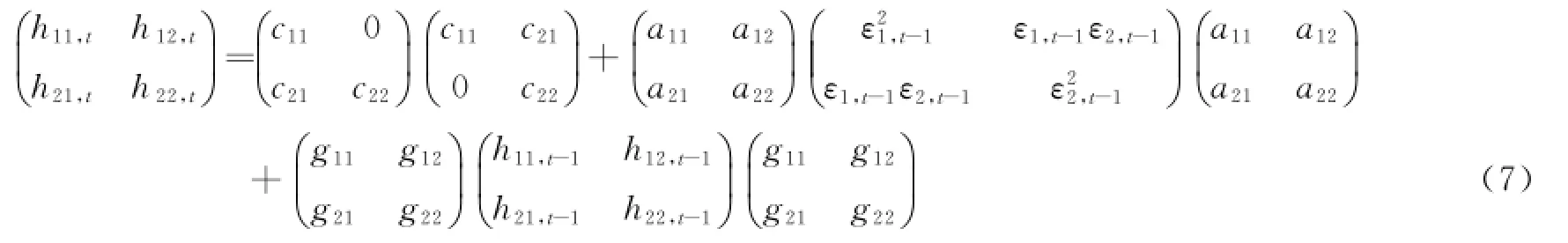
运用MGARCH-BEKK模型计算出的最优套期保值率为：

3.矩阵最小方差模型

假定现货市场期初的价格为P0≠0，第一期期末的现货市场价格未知，设为~P1。期货合约期初的价格为F0，第一期期末的价格未知，设为~F1。假定持有一份现货多头和一份期货多头，组合的收益率为：

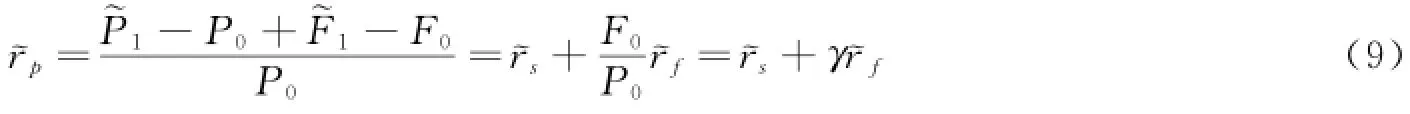
rs为现货市场的收益率，γ=F0/P0，~rf=（~F1-F0）/F0为期货市场的收益率。现假定投资者持有n份现货，m份期货多头，这该投资组合的收益率为：

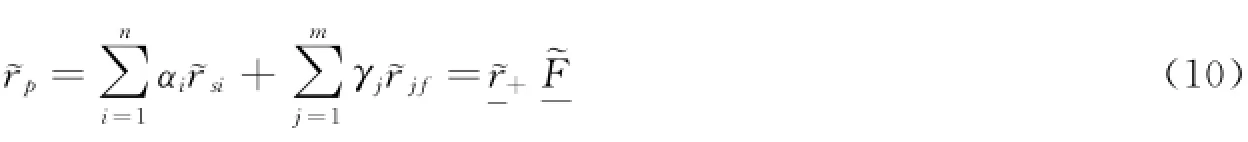
其中，αi现货组合的权重，′表示转置，加下划线表示矩阵。表示净现值为正，表示净现值为负。假定流动性溢价可以忽略，期货合约与远期合约的定价一样，所以有，即。根据上述假设，有E［~F］=0。

投资者方差最小化问题可表示为：γ-

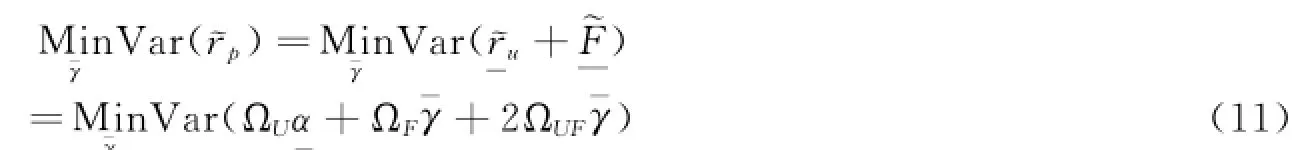
ΩS表示n*n的现货市场持有期收益率协方差矩阵，

ΩF表示m*m的期货价格收益率协方差矩阵，

ΩSF表示n*m的现货和期货市场收益率协方差矩阵。

一阶条件为：

解得：

矩阵套期保值方法是对单一合约套期保值方法的一种拓展，现货和期货都由一个合约扩展为多个合约，更符合经济活动中的实际情况，具有更强的实际意义。而且，根据金融经济学基本理论，产品种类更多，更完善的市场，资本配置效率更高。因此，我们可以预测采用多个期货合约管理利率风险能够显著提高风险管理效率。本文将运用市场实际数据对矩阵套期保值方法进行实证，检验其利率风险管理效果。

（二）套期保值效果的检验方法

在对套期保值效果进行检验的过程中，以往的相关研究主要根据套期保值的组合相对于未套期保值的组合的方差降低的比例e和收益率上升的比例k两个指标来反映套期套期保值的效果：

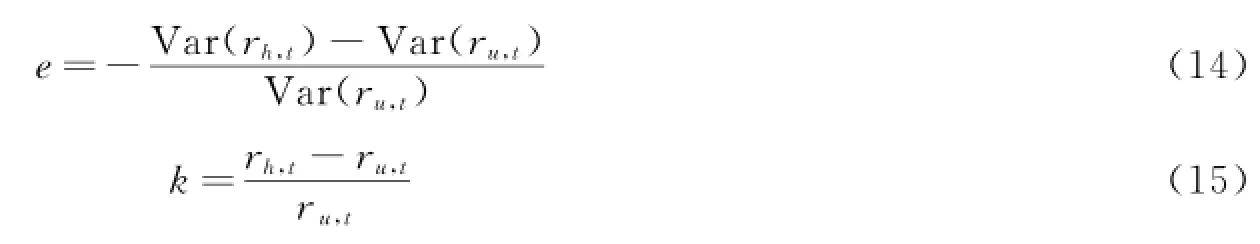
其中，ru，t表示未进行套期保值的组合即所持有现货的收益率；rh，t表示套期保值的组合的收益率rh，t=ru，t-h*rf，t；h*为最优套期保值比率。为了综合方差降低与收益增加两个指标对套期保值效果的反映，基于sharp比率的思想，我们提出了运用承担单位风险所获得的收益率的比率s来综合反应套期保值的效果，既能体现组合方差的降低，又能反映收益的变动：

s越高，表示承担单位风险所能获得的收益越大，套期保值效果越好。通过比较s的大小，可以反映出套期保值效果的优劣。

在一个套期保值期内，对于静态套期保值方法而言，h*是固定的，而对于动态套期保值方法而言，h*是随时间变动的。在计算套期保值组合的收益率时，动态套期保值方法的h*应采用每天的最优套期保值比率。在对样本外的动态套期保值效果进行检验时，模型的长期预测值都是长期均值，多步预测没有意义。因此只做一步预测，根据第t天及之前的信息预测t+1天的最优套期保值率，然后以此类推，对样本外的每一天都按照这种方式进行处理，最后再检验套期保值效果。

四、实证分析

（一）数据选取及数据处理

笔者选择2013年9月6日5年期国债期货交易开始到2014年12月31日共320个数据作为样本内数据，确定套期保值比例。假定银行套期保值的调整期为一个月，则选取2015年1月1日到2015年1月30日一个月共20个数据为样本外数据，检验套期保值效果。

1.国债期货合约

我国5年期国债期货合约的标的物是面额为100万元人民币，票面利率为3%的5年期名义标准国债，交易的期货合约包括四张合约，即3月、6月、9月、12月的国债期货合约。但每一天实际交易的合约只有距离到期日较近的三个合约同时交易，例如2015年2月时，就只有TF1503、TF1506、TF1509三个合约正在交易。笔者将不同年份相同月份交易的合约收盘价连接起来，该合约没有交易的日期收益率为0，形成期货合约组合。

在运用一种期货合约进行套期保值时，由于合约到期后将会进行交割，并且在国债期货的四张合约中，离到期日最近的合约的交易量比较大，交易最为活跃。所以假定银行进行利率风险管理时均选择离交割日最近的利率期货合约。笔者通过将离到期日最近的合约的收盘价进行连接起来的办法来产生连续的期货报价Pf，t。

2.银行股票价格

中国工商银行是目前中国最大的国有控股商业银行，拥有巨额的各类资产，且所涉及的品种全面，金额分布较为均匀，在我国商业银行中最具有行业代表性，所以本文选取中国工商银行作为利率风险管理分析的对象。银行股票价格数据选取CSMAR数据库中的日个股收盘价，收益率为考虑现金红利再投资的日个股回报率。

3.银行债券投资久期的计算

在运用久期套期保值方法时，需要计算商业银行资产负债的久期，但此变量根据现有公开资料无法直接计算得出。由于商业银行利率风险的主要来源为商业银行的债券投资业务，所以我们使用商业银行2013年年报中的债券投资久期替代①注：截至本文定稿之前，中国工商银行2014年的年报仍未公布，所以本文使用中国工商银行2013年年报所公布的相关数据。。假定中国工商银行非重组类债券投资在按剩余期限分组时，其债券投资结构与银行间债券总指数的债券结构相同，且从2013年12月31日到2014年12月31日期间银行债券投资组合的久期基本保持不变。据中国工商银行2013年年报显示，从剩余期限结构上看，3至12个月和1至5年的中短期非重组类债券投资增加，5年以上的长期非重组类债券比重比上年末有所下降。

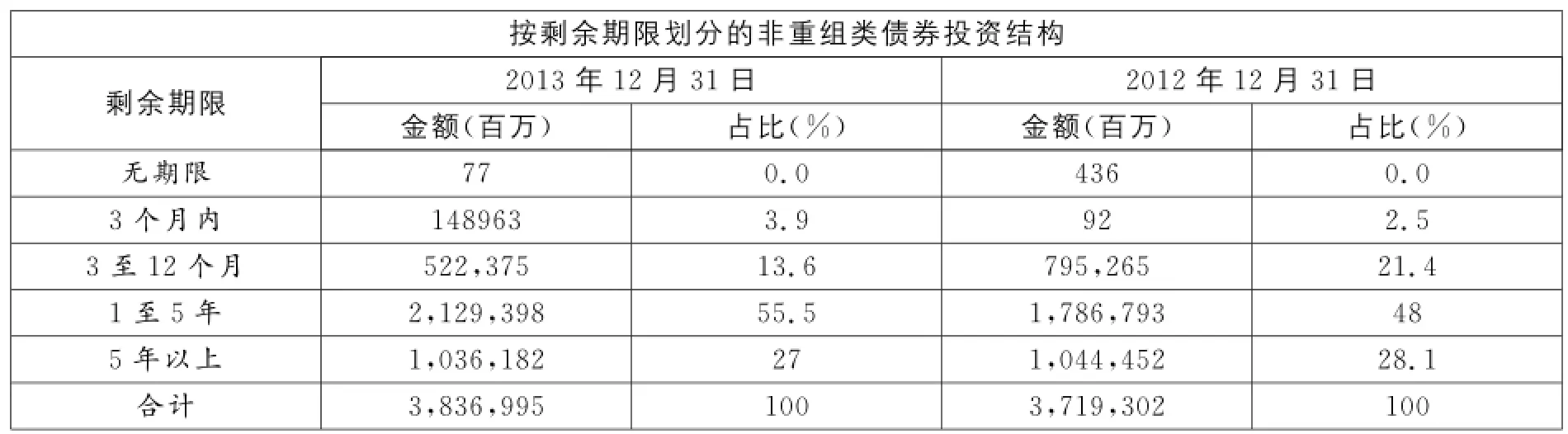
表1　2013年工商银行债券投资结构

笔者选取中国债券信息网的银行间债券总指数来反映银行间债券市场的总体情况，在计算银行的债券投资久期时采用2014年12月30日的“平均市值法久期”，具体取值如下：

表2　银行间债券总市值及平均市值法久期

由于中国工商银行债券投资结构与银行间债券总指数平均市值法久期的剩余期限划分不同，本文采用总市值加权平均调整平均市值法久期值，并将银行债券投资结构中一年以下债券投资合并以及无期限债券并入5年以上得到如表3所示结果。

采用价值加权平均法计算债券投资组合的久期，即：

其中：wi是该期限内债券的市值占总债券投资市值的权重；Di是期限i内的银行间债券久期。计算结果为：DS=3.51087

表3　处理后的银行间债券总市值及平均市值法久期

4.银行间利率互换

我国银行间人民币利率互换交易的产品众多，主要的参考利率有FR007（七天银行间回购定盘利率）、Shibor_3M（上海银行间3个月同业拆放利率）、Shibor_O/N（3个月的上海银行间隔夜同业拆放利率）以及1年期定期贷款利率。从参考利率产品的数量和交易量来看，FR007是银行间利率互换最主要的参考利率，以FR007为参考利率的利率互换产品的交易量高达65%以上。利率互换产品的成交期限分布广泛，从1个月到10年不等，其中1年期左右的中短期产品交易最为活跃。所以笔者选择成交量最大的FR007一年、FR007两年，FR007五年和Shibor_3M一年期利率互换交易，交易数据来自CSMAR数据库。

在利率互换合约成立时，合约的价值为零，即浮动利率的未来支付的现金流折现值与固定利率支付的现金流折现值相等。也可以认为在合约期限内，市场对浮动利率支付的预期与合约的固定利率相等。由于利率互换合约的交易期限较长，浮动利率在未来的预测基本无意义，所以本文采用利率互换合约中的固定利率代替浮动利率，利率互换合约的收益率计算方法如下：

（1）选取中国债券信息网公布的银行间固定利率国债收益率曲线作为当天的银行预期的利率期限结构，我国的利率互换付息频率为一个季度一次，对于利率期限结构中缺少的时点采用线性插值法补全。

（2）采用每日的互换合约中的固定利率报价减去利率风险管理日（2014年12月31日）相应合约的固定利率报价，计算出每个付息日的收益率，并运用所确定的利率期限结构折现，计算出相应的互换合约收益率。

具体计算公式为：

其中，Vswap，t表示第t天利率互换合约的价值，rfix，t表示第t天该合约的固定利率报价，rfix，0表示该合约成立时的固定利率报价，ri，t表示第t天银行预期的利率期限结构中合约第i次付息时的利率。

（二）数据处理结果

笔者所选样本中的银行股票、国债期货和利率互换收益率数据的基本统计描述如表4所示。

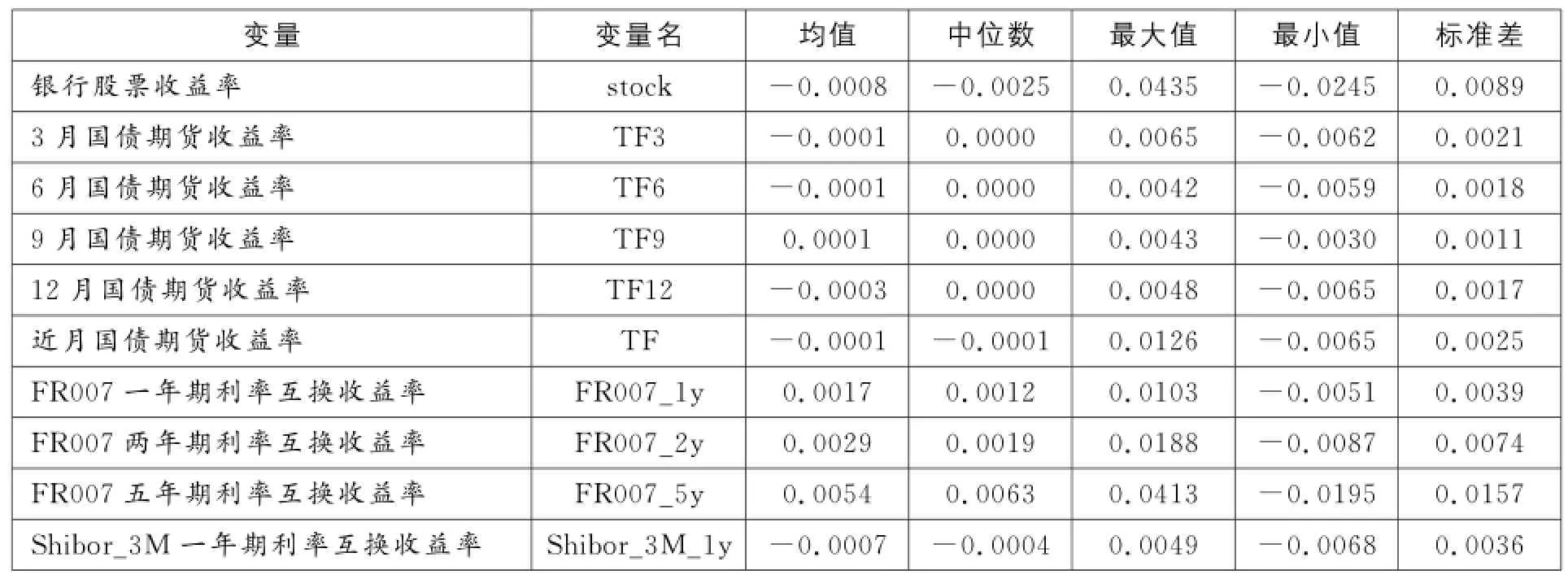
表4　样本数据基本描述统计

从表4可以看出，中国工商银行的股票收益率的均值为-0.0008，在样本区间内该银行的股票平均收益为负。收益率的最大值为0.04535，最小值为-0.0245，标准差为0.0089，说明在样本区间内，银行股票收益率的波动性较大。3月、6月、9月、12月的国债期货合约收益率的均值差别较小，收益率均值均在0附近，收益率的波动较小。FR007利率互换合约的平均收益率均为正，且随着利率互换合约交易期限的延长而逐步升高，这与相关经济理论相符。Shibor_3M的利率互换合约的平均收益率为负，说明3个月的短期利率的波动性较大。继续对样本数据进行一系列检验，根据样本数据所具有的特征，我们选择传统套期保值方法中的久期、最小方差、VAR模型和MGARCH-BEKK模型进行研究。

（三）套期保值比率的计算

1.久期方法

假定商业银行选用国债期货近月合约对冲商业银行的利率风险，且银行在利率风险管理期间债券投资组合的久期保持不变，根据东方财富网提供的可交割债券信息，TF1503的最便宜可交割债券是130015，即2013年发行的记账式附息（十五期）国债，在2014年12月31日最便宜交割债券的久期为DF=6.44487。

2.最小方差模型

根据商业银行股票收益率rs，t和利率期货收益率rf，t，套期保值比率为h，则现货与期货组合的收益率可表示为：

则最佳套期保值比率为：

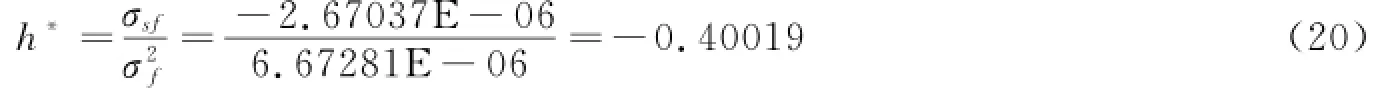
3.向量自回归模型（VAR）

通过对样本数据进行单位根检验和偏自相关检验，发现国债期货与股票收益率序列均是一阶单整序列，对OLS模型回归的残差进行单位根检验，发现不存在单位根现象，说明二者之间存在协整关系，不需要引入VECM模型进行改进。但是，对样本数据的自相关检验发现，样本数据存在自回归现象，即过去的现货和期货收益率会影响当前收益率。因此，针对该问题的改进方法是引入双变量向量自回归（B-VAR）。根据AIC和BIC最小准则，选择滞后阶数为1，模型的估计结果如下：

表5　VAR模型的估计结果

最优套期的计算结果如下：

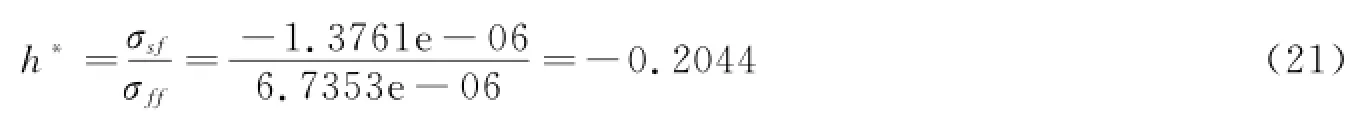
4.MGARCH-BEKK模型

本文根据样本数据运用MGARCH-BEKK模型计算的动态套期保值率基本信息如表6所示：

表6　动态套期保值利率统计特征

由上表可以看出，动态套期保值的均值为-0.128，与前述单期静态模型的计算结果符号相同，但数值上差距较大。动态套期保值比率的最大值为1.566，而最小值为-1.390，最大值与最小值之差和标准差的值都较大，这些数据表明在套期保值期内，最优套期保值比率的波动较大，而不是一直保持不变。

5.国债期货矩阵最小方差模型

在国债期货组合矩阵套期保值方法中，现货组合为银行股票收益率序列，现货组合权重由α数组定义，此时α=1，3月、6月、9月和12月的国债期货被用来构造套期保值组合。组合构成由γ′=（γ1，γ2，γ3，γ4）定义，根据矩阵套期保值原理公式可以算出：γ′=（0.4386，-1.7288，1.3221，0.3416）

该结果表明要对商业银行所面临的利率风险进行管理，需要持有的3月的国债期货合约比率为0.4386，6月的国债期货合约比率为-1.7288，9月的国债期货合约比率为1.3221，12月的国债期货合约比率为0.3416。

6.国债期货与利率互换均值最小方差模型

在国债期货与利率互换组合矩阵套期保值方法中，现货组合为银行股票收益率序列，组合权重由α数组定义，此时α=1，3月、6月、9月和12月的国债期货与FR007一年、两年、五年，Shibor_3M一年期利率互换合约被用来构造套期保值组合。组合构成由γ′=（γ1，γ2，γ3，γ4，γ5，γ6，γ7，γ8）定义，通过上述公式可以算出：γ′=（0.3840，-1.7837，1.5323，0.3451，-3.0686，1.8876，-0.2946，0.4905）

该结果表明要对商业银行所面临的利率风险进行管理，需要持有的3月的国债期货合约比率为0.3840，6月的国债期货合约比率为-1.7837，9月的国债期货合约比率为1.5323，12月的国债期货合约比率为0.3451，FR007一年利率互换合约比率为-3.0686，FR007两年利率互换合约比率为1.8876，FR007五年利率互换合约比率为-0.2946，Shibor_3M一年期利率互换合约比率为0.4905，国债期货合约所持有的头寸与仅采用国债期货进行利率风险管理的实证结果相近。

（四）利率风险管理效果比较

笔者对六种套期保值方法的样本内（2013年9月6日-2014年12月31日）风险管理效果进行检验，结果如表7所示。

从表7的实证结果可以看出，对于采用单一利率衍生工具管理利率风险的方法，运用久期套期保值方法的套期保值组合收益率的方差不仅没有下降，反而上升了6.1%，没有起到利率风险管理的效果。最小方差方法和VAR方法的套期保值组合的方差下降比例分别为1.35%和1.02%，利率风险管理效果不显著。采用动态套期保值方法的套期保值组合的方差下降比率为3.32%，在单一合约方法中利率风险管理效果最为显著，而且进行利率风险管理后组合的收益率不仅没有下降还有所上升，组合收益率上升了0.88%。对于采用多个利率衍生工具管理利率风险的方法，运用国债期货组合的套期保值组合的方差下降了2.92%，效果较好，但是组合的收益率下降较多，达到18.62%。同时采用国债期货和利率互换两种利率衍生工具的组合，方差下降比率最大，达到6.13%，利率风险管理效果最为显著。

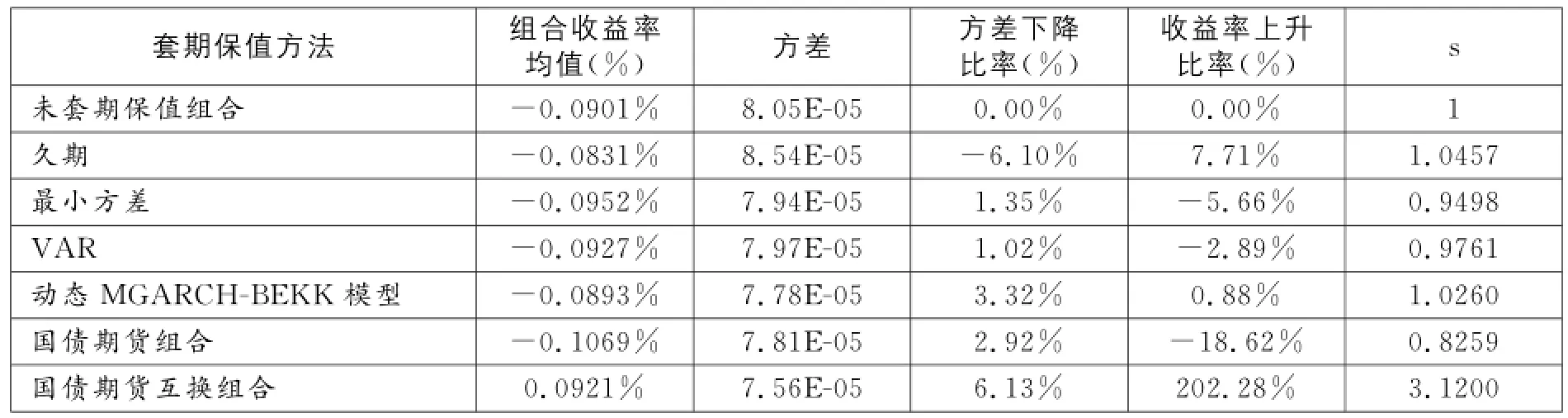
表7　样本内数据套期保值效果检验

根据上述实证结果分析，我们可以得到以下四点结论：

（1）久期套期保值方法的利率风险管理效果很差，相对于未套期保值组合，不但没有降低反而大幅度增加了套期保值组合的方差。造成这种情况的主要原因有：在我国国债市场上，主要以中长期国债为主，这通常会使得国债期货合约的最便宜交割债券的久期DF＞5，而商业银行资产和负债的久期一般较短。在久期套期保值方法中，选用与现货久期相近的期货合约，风险管理效果更好，所以该方法并不能起到利率风险管理效果；由于缺乏商业银行资产负债现金流的详细数据，本文对银行久期的计算值只是债券投资的近似值，这也会影响该种方法的套期保值效果。

（2）VAR模型的套期保值效果相对较差，模型估计的部分系数不显著，方差下降的比率仅为1.02%。

（3）动态套期保值方法的效果最好，不仅大幅降低了套期保值组合的方差，还提高了组合的收益率。在单一合约的套期保值方法中，动态套期保值方法具有明显的优势。

（4）通过对比最小方差、国债期货组合和国债期货互换组合基于最小方差理论的三种方法的结果可以看出，随着使用管理利率风险的工具数量增加，组合方差下降的比例增加，同时由于利率互换的加入，还使得组合的收益率有所上升。从综合指标可以看出，动态套期保值方法和国债期货互换组合的利率风险管理效果最好。

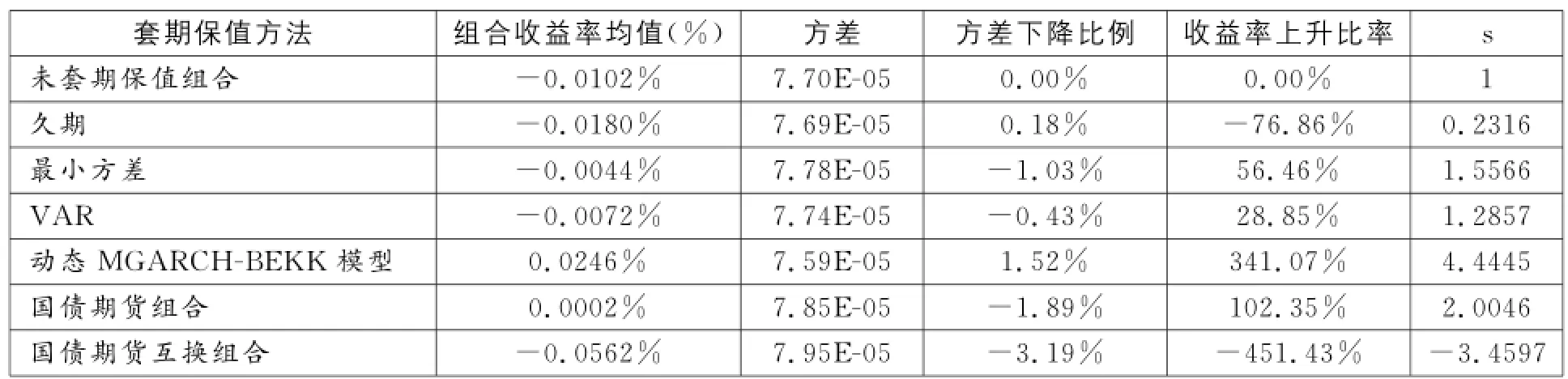
表8　样本外（2015年1月1日-2015年1月31日）数据套期保值效果检验

从表8可知，对样本外数据而言，在采用单一利率衍生工具管理利率风险的方法中，最小方差方法和VAR方法的套期保值组合的方差不仅未下降，反而有所上升，上升比例分别为1.03%和0.43%，表明这两种方法不具有外推性。采用动态套期保值方法的套期保值组合的方差下降比率仍能达到1.52%，组合的收益率也显著地上升了341.07%，说明动态套期保值方法具有很好的外推性。对于采用多个利率衍生工具管理利率风险的方法，运用国债期货组合和国债期货与利率互换组合的套期保值组合的方差在样本区间外均有所上升，上升比率分别为1.89%和3.19%，组合的收益率也发生了显著变化。因此，静态套期保值方法不具有较好的长期外推性，应使其动态化，实时根据市场情况进行调整。

对于样本外数据而言，不考虑久期套期保值方法的特殊表现，除动态套期保值方法外，各套期保值方法均使得套期保值组合的风险和收益率有所上升。这主要是由于样本外数据的股票和国债期货收益率上升，而根据样本内数据计算出的最优套期比率为正，所以导致的套期保值组合收益率的上升。最小方差、VAR模型、国债期货组合和国债期货互换组合这四种静态方法的共同缺点是对样本外数据而言，组合的方差上升，利率风险管理效果较差。

综合收益率和方差两个方面，动态套期保值方法的效果最好，不仅降低了套期保值组合的方差，还更多的提高了组合的收益率。但在实际运用中需要注意的是，波动比较剧烈的动态套期保值模型在套期保值时需要经常性的对仓位进行调整，波动变化不是很剧烈的模型则不需要进行过多次数的调整。本文中动态套期保值模型的波动率较大，实际运用中的套期保值成本比较高。

（五）适用于我国商业银行的利率风险管理方法讨论

根据上述实证结果，我们可以发现由于我国国债期货市场处于发展阶段，产品种类较少，久期的套期保值方法暂时不适用于我国商业银行运用利率期货进行利率风险管理；对样本内和样本外数据而言，单一期货合约的最小方差模型和VAR模型的套期保值效果均不是很好。最后我们可以发现，单一期货合约的MGARCH-BEKK模型和矩阵套期保值方法较适用于目前我国商业银行运用国债期货进行利率风险管理。前者套期保值效果相对较好，能同时兼顾风险和收益两个方面。后者，风险管理效果最好，能同时使用场内和场外的利率衍生工具，风险管理成本低，在套期保值期内无需调整即可大幅降低套期保值组合的方差。并且由于两种套期保值方法对利率的期限结构以及市场的发展程度没有严格的要求，针对我国目前发展不成熟的国债期货及场外利率衍生工具市场具有普遍的适用性。

五、结 论

利率风险管理是商业银行日常经营中的一个重要方面，利率衍生工具是规避利率风险重要工具。本文在对利率风险管理的研究中，主要运用久期、最小方差模型、VAR模型、MGARCH-BEKK模型和矩阵最小方差模型五种方法研究了运用国债期货合约及利率互换两种金融衍生工具对商业银行利率风险的管理的效果。研究结果表明无论对于样本内还是样本外数据，在单一合约套期保值方法中，动态套期保值方法明显优于静态套期保值方法，但在实际运用中动态套期保值方法的成本可能较高。由于我国国债期货市场的处于发展阶段，产品结构不全面，产品种类稀少，久期的套期保值方法效果不佳，暂时不适用于我国商业银行的利率风险管理。通过对上述套期保值方法的比较我们发现，MGARCHBEKK模型和矩阵最小方差模型较适用于目前我国商业银行的利率风险管理，但需要根据商业银行自身利率风险变化和市场情况变动，实时调整套期保值比率。此外，由于我国国债期货刚刚开始交易，且商业银行，保险公司等机构交易者不能参与交易，国债期货市场交易量小，交易不活跃，交易的数据并不能完全反应国债期货交易市场的情况，所以各套期保值方法的效果不是很明显。在国债期货市场交易活跃之后，期货和现货之间的信息传递、市场参与者行为等一系列的因素也会影响套期保值的效果。最后，由于笔者只研究了采用国债期货和利率互换两种利率衍生工具来管理利率风险，金融市场中还有其他金融工具例如，债券远期、债券期权、利率期权等，也可以用来管理利率期货。在目前我国金融市场发展不成熟的状况下，对这些衍生工具加以综合运用，将能更好对利率风险进行管理，提高管理效率。

［1］ 佟孟华（2011）.沪深300股指期货动态套期保值比率模型估计及比较.数量经济技术经济研究，4.

［2］ 王 骏、张宗成、赵昌旭（2005）.中国硬麦和大豆期货市场套期保值绩效的实证研究.中国农业大学学报，10（4）.

［3］ 王 骏、张宗成（2006）.中国有色金属期货市场套期保值绩效的实证研究：2000-2004年.中国地质大学学报，6（1）.

［4］ Baillie R T，Myers R J.，（1991）.Bivariate GARCH estimation of the optimal commodity futures hedge.Journal of Applied Econometrics，6（2）.

［5］ Carcano N，Foresi S.（1997）.Hedging against interest rate risk：Reconsidering volatility-adjusted immunization. Journal of Banking and Finance，21（2）.

［6］ Cecchetti S G，Cumby R E，Figlewski S.（1986）.Estimation of the optimal futures hedge.The Review of Economics and Statistics，70（4）.

［7］ Daigler R T，Copper M（1998a）.A future duration-convexity hedging method.The Financial Review，33.

［8］ Ederington L H.，（1979）.The hedging performance of the new futures markets.The Journal of Finance，34（1）.

［9］ Franckle C T，Senchack A J.，（1982）.Economic considerations in the use of interest rate futures.Journal of Futures Markets，2（1）.

［10］Ghosh A（1993）.Hedging with stock index futures：estimation and fo recasting with error correction model.The Journal of Futures Markets，13.

［11］Herbst A F，Kare D，Marshall J F（1993）.A time varying，convergence adjusted，minimum risk futures hedge ratio. Advances in Futures and Options Research，6.

［12］Hilliard J E.，（1984）.Hedging interest rate risk with futures portfolios under term structure effects.The Journal of Finance，39（5）.

［13］Kolb R，Chiang R.，（1981）.Improving hedging performance using interest rate futures.Financial Management，10（4）.

［14］Lien D（1996）.The effect of the cointegration relationship on futures hedging：a note.Journal of Futures Markets，16.

［15］Myers R J，Thompson S R（1989）.Generalized optimal hedge ratio estimation.American Journal of Agricultural Economics，71.

［16］Rendleman Jr R J（1999）.Duration-based hedging with Treasury bond futures.The Journal of Fixed Income，9（1）.

高 菲，中国银监会四川监管局。

■责任编辑：刘金波

The Efficiency of Using Financial Derivatives to Manage the Interest Rate Risk of Chinese Commercial Banks

Wang Jinzhong（Southstern University of Finance and Economic）
Gao Fei（China Banking Regulatory Commission Supervision Bureau of Sichuan）

With the development of futures market in China and interest rate liberalization，how to use interest rate futures to effectively hedge interest rate risk of commercial banks has attracted more and more attention.In this paper，according to the characteristics of data，we used the hedging methods based on duration，minimum variance theory，VAR model，MGARCHBEKK model and minimum variance matrix model to research using bond futures and interest rate swaps to hedge the interest risk of commercial banks.By comparing the hedging pros and cons of each model，the hedging models based on dynamic hedging model and minimum variance matrix model are more effective and suitable for China’s commercial banks. Key words：interest rate futures；hedging；interest rate risk of commercial banks

■教育部人文社会科学研究规划基金项目（15YJA790057）

■作者地址：王晋忠，西南财经大学金融学院；四川成都，611130。Email：jzwang@swufe.edu.cn。