蛇形微通道气液两相流动特性

周云龙，孙振国

（东北电力大学能源与动力工程学院，吉林省 吉林市 132012）

引言

近年来，微通道技术已成为化工行业的重要研究方向[1]。微尺度下的流动随着流体性质以及流动工况的变化不同于常规尺度。蛇形管在许多工业应用中都显示出其独特的效应。宋正梅[2]对直入直出型、直角S型、圆角S型微通道在相控阵天线上的应用进行了模拟，结果表明S型通道可以使T/R组件下方流过更多的流体，这无疑会使组件热交换更加充分。Wen等[3]研究了小管径蛇形管内的流动，结果显示蛇形管内泡状流的传热系数较常规通道有所增大。Donaldson等[4]采用T型混合方式，在当量直径1.0563 mm的蛇形通道对空气、水的流动特性进行实验，发现了泡状流、塞状流、不稳定塞状流、弹状流等流型。白璐等[5]采用氮气、含有表面活性剂的甘油溶液为两相工质，通过T型错流方式在并行微通道内观测到泡状流、弹状流、分层流等典型流型，并指出主通道与支通道中的气泡大小不同。李洪伟等[6]将平滑Wigner三谱切片理论应用到多相流识别中，发现氮气-水的两相流型主要有分散泡状流、弹状流和环状流。Ribatski等[7]在0.4 mm管道中对R134a的流动情况进行了详细的分析，并观测到泡状流、弹状流、环状流。进一步指出不同流型对传热特性的影响也不尽相同。

蛇形管作为换热器的一种，广泛应用于核能、空调低温制冷以及化工领域中。但是，大多数的气液两相流研究都集中在直管道内。实际应用中，由于空间的局限性，需要大量的弯管结构。目前关于蛇形管的研究多见于常规尺度，微尺度下的流动特性鲜有报道。相比于常规直管道，对微米级别蛇形管内两相流的认识比较缺乏，有必要对蛇形管内的流动进一步研究。本文以空气-水为实验工质，利用高速摄像仪以及图像采集系统，对Y型混合器内气液两种混合模式下的流动进行了对比分析，以完善蛇形结构微通道气液两相流型以及相分布的认识，为实际工程应用提供一定的理论依据。

1 实验系统

1.1 微通道定义及尺寸

不同的学者对微通道的定义有不同的标准，Mehendale等[8]以当量直径作为通道划分的依据，认为直径为1～100 μm时可作为微通道，而Kandlikar[9]认为微通道当量直径应该划分在10～200 μm才比较合适。Bretherton[10]则提议当Eo＜0.84时，可认为是微通道。

式中，Eo为Eotvos数，ρg与ρl分别为气相和液相的密度，kg·m-3；Dh为微通道当量直径，m；σ为表面张力，N·m-1；g为重力加速度，m·s-2。

本文微通道形状如图1所示，通道截面为矩形（0.8 mm×0.1 mm），求得当量直径为177.8 μm，Eo为4.2×10-3，符合Kandlikar和Bretherton的定义。实验中通道所用材质为PDMS-玻璃。Ⅰ、Ⅱ为两半圆，其内径为3 mm、外径为4.6 mm。进口段长度均为10 mm，通道a、b、c 3段的有效长度均为50 mm，两相流采用夹角θ为50°的Y型进口。

图1 蛇形微通道 Fig.1 Serpentine microchannel

1.2 实验装置

非机械微流体驱动方式容易受到通道表面和流体性质等的影响，在本次多相流实验控制中采用压力驱动方式，实验中压力驱动所用注射泵型号为SDS-MP10（最大量程1200 ml·h-1，调整步距0.1 ml·h-1，速度控制精度±2%）。为清晰捕捉各种典型的流型图像，所用高速摄像仪型号为HSS4G(德国LaVision公司,最大分辨率1024×1024，最大帧频2000 fps)。光源采用色温6400K的三基色光管，芯片背面铺设有硫酸纸可使光线均匀分布。进口和出口部位通过不锈钢金属细管(内径0.5 mm，外径0.7 mm)与聚四氟乙烯导管(内径0.5 mm，外径0.9 mm)连接，为防止工质对通道堵塞，在注射泵和导管之间安装了过滤器。两相流体在出口处进行气液分离，利用高精度电子天平和气体流量计，分别测量一段时间内水、空气的流量。实验系统如图2所示。

实验环境为常压，温度18.6℃。实验中将微通道在垂直面内横向放置，对两个进口分别采用图3所示方案（上气下液型以及上液下气型）。由于PDMS的疏水亲油性，实验前先用0.06%的NaHCO3溶液将通道壁面润湿，通过调节两相的流速，待流型稳定5 min后，用高速摄像仪采集各工况下的不同流型。

图2 实验系统 Fig.2 Experimental system

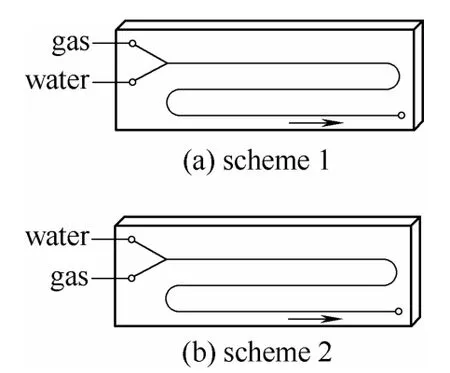
图3 两种实验方案 Fig.3 Two kinds of experimental scheme

2 实验结果与讨论

赵建福等[11]对内径12.7 mm的90°弯管进行了空气、水两相流型的研究，结果发现了弹状流、弹/环过渡流、环状流3种流型，并指出弯管内二次流作用以及气泡、气核的出现使得流谱由单相流的Dean双涡结构改为螺旋结构。柴磊等[12]对长10 mm的扇形凹穴型、三角凹穴型两种周期性扩缩微通道内的气液两相流型进行了考察，发现的主要流型有间歇流以及分离流。Kawahara等[13]以氮气、水为工质，在直径100 μm的圆形通道中主要观测到一些过渡流型，实验中并没有发现泡状流以及搅拌流。而Saisorn等[14]在直径150 μm的圆形通道中也没有发现泡状流。Pansunee 等[15]在当量直径267 μm的铜基矩形通道中进行了空气、水两相流实验，结果发现了分段流、液环流、拉断的液环流、环状流。由于微通道形状、尺寸以及流体性质等多种因素的影响，使得不同学者对流型观测到的结果也不同。在方案1实验中，观测到的主要流型有弹状流、长弹状流、波状分层流、弥散流；方案2中主要流型有弹状流、波状分层流、弥散流。图4、图5分别给出了方案1、2的流型图，其中WeG、WeL分别为气、液相Weber数，二者定义为：由图可知，这两种混合模式中弹状 流区域都占据了流型图的较大部分，相对于前者，后者的弹状流区域边界线向右有所偏移，而且分层流到弥散流的过渡线也向右上方偏移，这是因为在上液下气型的混合模式中，气液两相的相对位置发生了变化，由于弯道的二次回流使其产生了较强的扰动，进一步表明混合模式对各自的流型区域具有一定的影响。

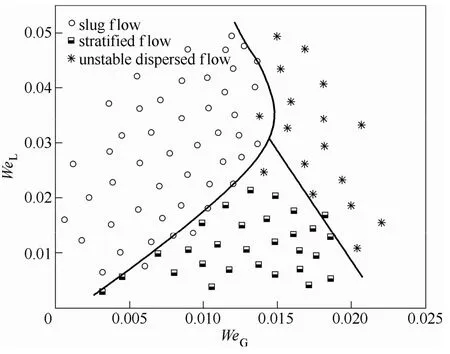
图4 方案1流型 Fig.4 Flow patterns map of scheme 1

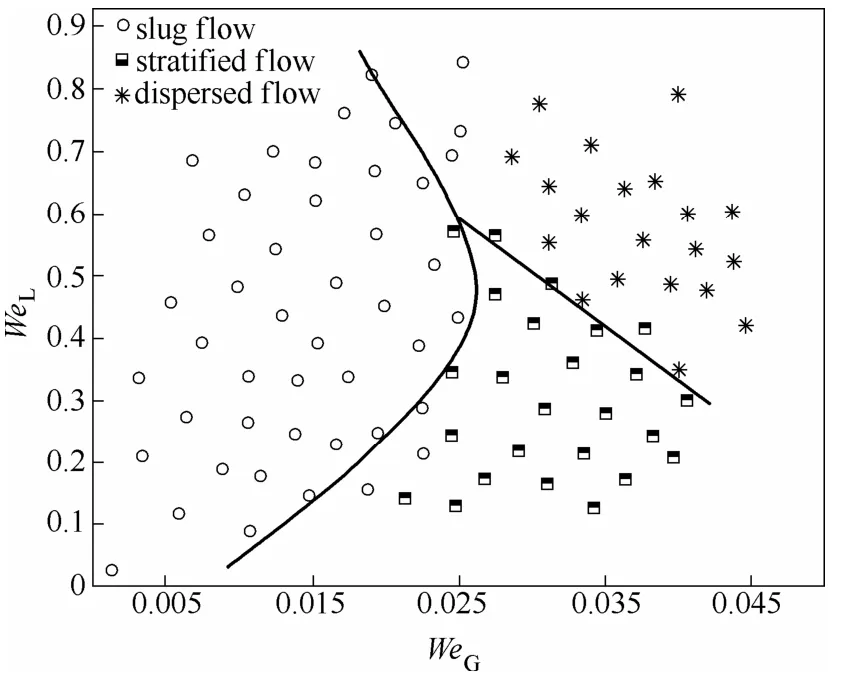
图5 方案2流型 Fig.5 Flow patterns map of scheme 2

2.1 弹状流

如图6所示，当气相表观速度jG=1.389 m·s-1，液相表观速度jL=0.122 m·s-1时可以采集到典型的弹状流。气弹通过弯道进入每一条水平直管道后，起初形状都不稳定，其头部比较尖锐而尾部比较平缓，气弹头部在运动方向上受到壁面约束以及液相的剪切发生一定的形变，在运行一段距离稳定后，此时表面张力的作用大于弯道壁面约束所带来的影响，头部逐渐变得圆润，但是尾部没有之前的那样平缓，而是略带有一定的角度，向气体内部凹陷。

进一步增加气相速度，发现气弹产生的位置将由两相汇合的地方逐渐后移，而且此时由于气体“飘”在液体上方，较高的气相流速下，液相和气相间的剪切力将显著增加，从而导致气弹产生的频率也较之前的有所提升，并且气弹长度也会增加。马友光等[16]在气相速度较高时也观测到类似的结果。图7显示了气相表观速度jG=1.738 m·s-1，液相表观速度jL=0.139 m·s-1时，产生长气弹的过程。

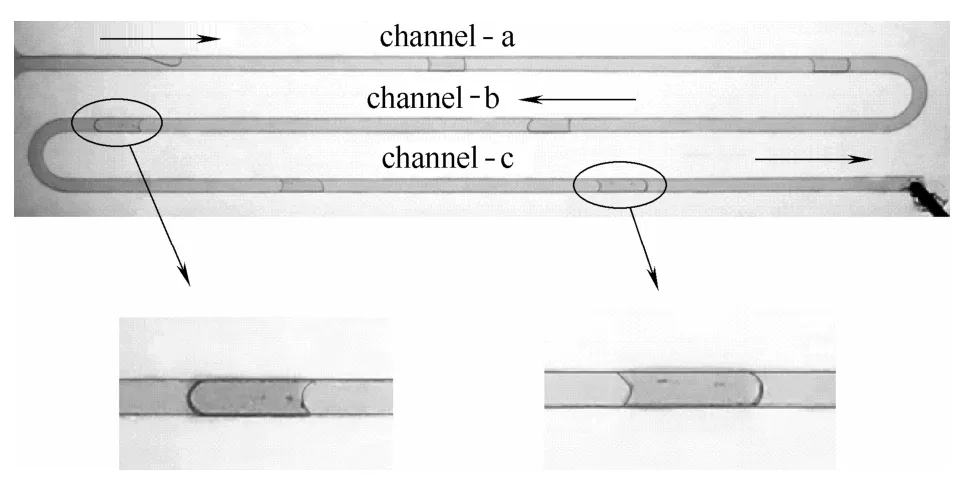
图6 方案1：弹状流 Fig.6 Scheme 1: slug flow

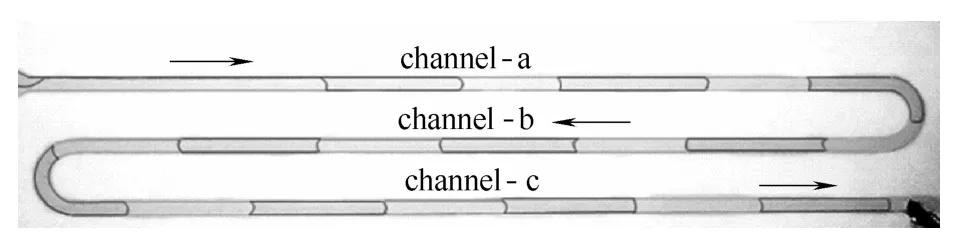
图7 方案1：拉长的弹状流 Fig.7 Scheme 1: elongated slug flow

Fukano等[17]曾将弹状流特征描述为气弹头部和尾部都是规则的半球形。而文献[18]对空气-水两相流动特性进行了数值研究，结果发现所形成的气弹并没有对称，其头部比较尖锐，而尾部比较平缓。Yao等[19]以PMMA为材质，对截面尺寸750 μm ×280 μm的Y型微通道进行了研究，发现气弹形状及大小与We有关。当We>3.1时，液膜厚度逐渐增加，气弹也随之与壁面脱离，并且在气体速度较高时，气弹头部将变得更加尖锐，而尾部则更加扁平。当We较小时，由于此时表面张力占优势，才使得气弹尾部呈椭球形。这说明在两相流速不同的情况下，弹状流的形状并不是唯一的。本实验中，当jG=1.736 m·s-1，jL=0.278 m·s-1时，可得到方案2下的弹状流型。由图8可以看出，此时气弹头部形状仍然比较圆润，而尾部向内凹陷。认为气弹的形状受到表面张力与液相剪切共同的影响，在气弹刚产生时，其头部表面张力占优，使得该处比较圆润，但尾部由于液相的剪切作用，从而向内凹陷。在流动过程中，当气弹经过弯道时，由于壁面的约束，使其头部略有变形，在进入水平段以后，其形状才逐渐得以恢复。

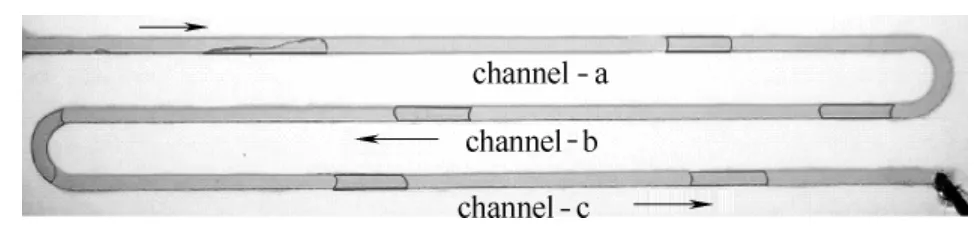
图8 方案2：弹状流 Fig.8 Scheme 2: slug flow

Yao等[19]分析了弹状流的形成过程，考虑到惯性效应的存在，提出如下气弹长度关联式

图9 气弹长度与两相流量比之间的关系 Fig.9 Relationship between gas slug length and flow ratio

由图可知，气弹长度和流量比基本呈线性关系，但是二者的斜率不同，这与各自的流动方式有关。方案2数据拟合的曲线斜率明显较方案1的大，这是由于方案2中气相“背着”液相在经过弯道的流动过程中，产生了较强的扰动。

Xu等[20]对弹状流的形成进行了详细的研究，将该过程分为两个部分，起始阶段气弹大小与通道宽度有关，随后其长度进入延伸阶段，受控于两相流率比，该过程的气弹长度L由L1和L2组成。通过推导，L与φ也呈线性关系。

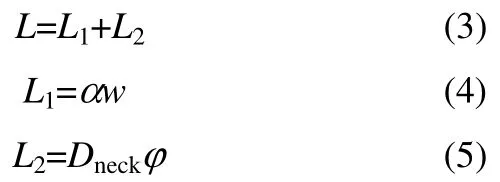
将式（3）～式（5）联立，可得

式中，L为气弹长度，mm；l为液塞长度，mm；w为微通道宽度，mm；jG、jL分别为气、液相表观速度，m·s-1；α、β、Dneck为与微通道结构有关的参数；φ为两相流速比。

图10反映了两种方案下液塞长度的对比情况，由图可知，起初液塞长度有线性增长的趋势，但这种趋势并没有一直保持下去，随着流速的增加，逐渐呈现非线性函数的特点，将所有实验数据进行多项式拟合，得到各自表达式如图10所示，这主要是由于较高的流速下弯道的扰流效应有所增强，对液塞长度的变化产生了直接影响。

图10 液塞长度与两相流量比之间的关系 Fig.10 Relationship between liquid slug length and flow ratio

此外，在实验中还发现，当液相速度非常低、气相速度不太高的情况下，可以利用圆弧诱导产生气弹。图11、图12分别显示了两种方案下圆弧诱导气弹的过程。方案1中的气流在经过圆弧Ⅰ时紧贴外壁，并经过拉伸、断裂两个过程。而方案2中，气流在流动过程中受到上方液相的阻碍，不能及时经过弯道，而是先向上进行膨胀。当主体进入弯道后，在液相剪切的作用下，气流沿着内壁进行拉伸，最后才断裂。这两种不同的混合方式所形成的气弹尾部都是向内凹陷。进一步表明气弹的形状并不唯一，受到流速、通道结构等多种因素的影响。

图11 方案1：圆弧诱导产生的弹状流 Fig.11 Scheme 1: arc induced slug flow (jG=1.042 m·s-1，jL=0.052 m·s-1)

图12 方案2：圆弧诱导产生的弹状流 Fig.12 Scheme 2: arc induced slug flow (jG=0.694 m·s-1，jL=0.104 m·s-1)

2.2 波状分层流

Kositanont等[21]根据甲苯难溶于水的特点，在曲率半径为0.5 mm，截面为矩形（100 μm×40 μm）的蛇形微通道内，对内置有指引壁（图13）以及表面改性这两种不同的结构进行了数值模拟，结果发现前者由于离心力的作用，甲苯和水在弯道处的分布位置发生了切换。而后者的直管段以及弯道处都存在着比较稳定的分层流。虽然煤油密度明显小于水的密度，但Burns等[22]在实验中发现煤油相竟然可以在水相下面稳定流动。在实验过程中也观测到类似上述的现象，如图14、图15所示。从图中可以看出，二者相界面有所差异，前者界面比较曲折，而后者相对较为平缓。而且这两种混合方式下的气、液相在弯道处的位置分布明显不同。方案1中的气流流经弯道Ⅰ时偏向于外壁，而在流经弯道Ⅱ时偏向于内壁。方案2则恰好与此相反。孟勐等[23]曾以R141b为工质，对内径6 mm的石英玻璃管进行了观测，发现在不同的热流-热量比下弯头处出现了弹状流、塞状流、分层-波状流3种不同的流型，进一步说明弯头内、外壁面的核化存在着较大的差异。因此，在实际应用中，为防止传热恶化，应对弯头的不同侧壁面给予注意。

图13 内置有指引壁的通道[21]Fig.13 Microchannel with guideline structure[21]

图14 方案1：波状分层流 Fig.14 Scheme 1: wavy stratified flow (jG=1.042 m·s-1，jL=0.035 m·s-1)

图15 方案2：波状分层流 Fig.15 Scheme 2: wavy stratified flow (jG=2.897 m·s-1，jL=0.556 m·s-1)

针对以上波状分层流，建立了计算液膜厚度的理论模型，如图16所示。由于气液界面与通道在水平方向上并非严格平行，所以可将液膜段分割为若干梯形区，借助ImageJ图像处理工具，设定好像素比例，先得到梯形区的上下底hi1、hi2，然后计算每一梯形区的等效高度δi，最后求得多个梯形区等效高度的平均值作为该段通道液膜的平均厚度，见式(7)、式(8)。

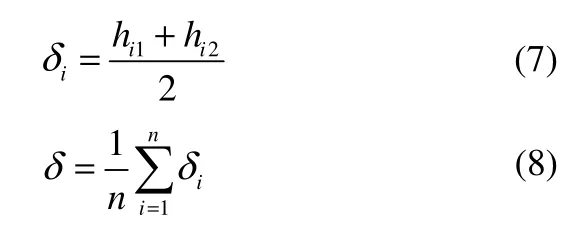
图16 理论模型 Fig.16 Calculation model

通过对通道a、b、c 3段的液膜平均厚度进行统计分析，得到液相表观速度jL为0.556 m·s-1时，这3段液膜平均厚度δ随气相流速的变化关系如图17所示。当液相表观速度一定时，增加空气流速会使液膜厚度减小，尤其是液膜厚度较大时，空气流速的增加会使其迅速下降。随着气相速度的进一步增加，液膜厚度变化逐渐趋于平缓。由Steinbrenner等[24]提出的两相分层模型[式(9)]可知，当气相速度增加时，气相和液相之间的剪切力也随之增加，而两相和壁面之间的切应力几乎没有变化或者变化很小，这样必然使液相体积减小，气相体积增大，最终使液膜厚度降低。

式中，τwG为壁面和气相间的切应力，Pa；τwL为壁面和液相间的切应力，Pa；τi为两相之间的切应力，Pa；AG、AL分别为气、液相的面积，m2；PG、PL分别为气、液相湿周，m；Pi为两相接触面的有效周长，m。

图17 方案2：气相表观流速对液膜平均厚度的影响 Fig.17 Scheme 2: average thickness of liquid film according to jG

由图1可知，通道a段液膜平均厚度要大于b、c段，通道b段液膜平均厚度最小。从图15可以看出，通道b段下游弯道Ⅱ处气相区域颜色较深，表明此刻气体密度较大，这说明b段的气相比较多。这是由于空气在流动过程中由于前后两个弯头的作用使其所受阻力较大，这样气体在通道b中容易聚集，抑制了该段液膜的生长。由于实验段垂直放置，相比通道b段，a、c段中的液相相当于“骑”在气相上方，在流动过程中对气体造成一定的挤压，从而使气相部分有所减小，这样液膜厚度相对b段要大一些。另外，c段离出口最近，故c段液膜厚度相对a段要小一些。

2.3 弥散流

在方案1实验中，当jG为1.304～2.531 m·s-1(ReG为 15.459～30.637)，jL为 0.068～0.271 m·s-1(ReL为10.526～48.274)时，观测到不稳定流型出现，如图18所示，通道a段主要是分层流，通道b段出现了大小不等的块状流，上游的气水混合物流经弯道后，在通道c段出现了弥散流，气流中夹带了大量的微小液滴。而方案2产生的弥散流较为稳定，如图19所示。在方案2中，通道a段呈现出分层流，经过弯道Ⅰ后气流中携带着许多小液滴，由图19可知，通道b段液滴主要集中于底层，而通道c段液滴却集中在上层。并且弯道Ⅱ中的液滴分布向内侧集中，相比弯道Ⅰ，其数量明显增加。将图15、图19对比可以看到，当流型为分层流时，由于惯性效应的影响，只有弯道Ⅰ处气流向内侧集中，而弯道Ⅱ处的气流却偏向于外侧。当流型为弥散流时，弯道Ⅰ、Ⅱ的气流分布均偏向于内侧。表明不同的流型对气液两相的位置分布会有较大的影响。

图18 不稳定流型 Fig.18 Unstable flow regime (jG=2.389 m·s-1，jL=0.139 m·s-1)

图19 方案2(上液下气)：弥散流 Fig.19 Scheme 2(up liquid and down gas): dispersed flow (jG=3.681 m·s-1，jL=0.694 m·s-1)

针对以上两种混合方式，通过气体体积流量计得到气相流量，并计算相同时间内采集的液相流量，进而得到该流型下气体夹带液滴的份额，并将实验数据进行拟合，得到如下预测关联式

其中

式中，p1、p2、p3见表1；ecal、eexp分别对应液滴份额的预测值与实验值；Δe为液滴含量的相对偏差。如图20所示，由式(10)得到的曲线与实验数据吻合相对较好，通过式(11)计算得到的相对误差在±5%以内，如图21所示，进一步表明以上关联式可以进行很好地预测。

表1 系数p1、p2、p3Table 1 Coefficients of p1，p2and p3

图20 微小液滴携带份额 Fig.20 Share of entrained liquid droplets

3 结论

本文以空气、去离子水为两相介质，采用Y型入口，针对气液两种混合方式，利用可视化实验方法，对比了蛇形微通道内的流动特性，并分析二者的不同之处，得到以下结论。

（1）本实验对蛇形微通道观测到的稳定流型主要有弹状流、波状分层流以及弥散流。

图21 微小液滴份额误差曲线 Fig.21 Tiny droplets share error curve

（2）不是所有的气弹头部、尾部形状都是规则的半球形，这与微通道的形状以及流体的流动参数有关。在流速比较低的情况下，可以利用圆弧诱导产生弹状流，该过程可分为拉伸、断裂等阶段。

（3）不同混合方式下的波状分层流有着明显的区别，相界面的平缓程度以及各相在弯道壁面处的位置分布与此有较大关系。

（4）高速气流所携带液滴的份额与二者Reynolds数的比值有关。

符号说明

Dh——微通道当量直径，mm

e ——气流携带微小液滴的份额，%

hi——第i个梯形区的上、下底，μm

n ——梯形区的个数

Re ——Reynolds数

We ——Weber数

δ ——液膜平均厚度，μm

δi——第i个梯形区的等效高度，μm

下角标

G ——气相

g ——气相

L ——液相

l ——液相

w ——壁面

[1] Fu T T, Ma Y G, Funfschiling D, Zhu C Y, Li H Z.Squeezing-to- dripping transition for bubble formation in a microfluidic T-junction [J].Chemical Engineering Science, 2010, 65(12): 3739-3748.

[2] Song Zhengmei(宋正梅).Research about the technique of microchannel cooling on active phased array antenna.[D].Xi’an: Xidian University, 2013.

[3] Wen M Y, Ho C Y, Jang J K.Boiling heat transfer of refrigerant R-600a/R-290-oil mixtures in the serpentine small diameter U-tubes [J].Applied Thermal Engineering, 2007, 27(14/15): 2353-2362.

[4] Donaldson A A, Kirpalani D M, Macchi A.Curvature induced flow pattern transitions in serpentine minichannels.[J].International Journal of Multiphase Flow, 2011, 37: 429-439.

[5] Bai Lu(白璐), Zhu Chunying(朱春英), Fu Taotao(付涛涛), Ma Youguang(马友光).Gas-liquid flow distribution of parallel microchannels [J].CIESC Journal(化工学报), 2014, 65(1): 108-115.

[6] Li Hongwei(李洪伟), Zhou Yunlong(周云龙), Yang Yue (杨悦), Sun Bin(孙斌).Time-frequency characteristics of smoothed Wigner tri-spectrum slices of nitrogen-water two-phase flow pattern [J].CIESC Journal(化工学报), 2013, 64(10): 3571-3580.

[7] Ribatski G, Tibirica C B.Flow patterns and bubble departure fundamental characteristics during flow boiling in microscale channels [J].Experimental Thermal and Fluid Science, 2014, 59: 152-165.

[8] Mehendale S S, Shah R K, Jacobi A M.Fluid flow and heat transfer at micro and meso-scales with application to heat exchanger design [J].Applied Mechanics Reviews, 2000, 53(7): 175-193.

[9] Kandlikar S G.Fundamental issues related to flow boiling in minichannels and microchannels [J].Experimental Thermal and Fluid Science, 2002, 26(2/3/4): 389-407.

[10] Bretherton F P.The motion of long bubbles in tubes [J].Journal of Fluid Mechanics, 1961, 10(3): 166-188.

[11] Zhao Jianfu(赵建福), Gabriel K S.The study of gas-liquid two-phase flow pattern in a 90°bend under micro-gravity conditions [J].Journal of Engineering Thermophysics(工程热物理学报), 2004, 25(5): 801-803.

[12] Chai Lei(柴磊), Xia Guodong(夏国栋), Li Jian(李健), Zhou Mingzheng(周明正).Flow pattern and evolvement characteristics of two-phase flow in microchannel with periodic expansion-constriction cross sections [J].CIESC Journal(化工学报), 2013, 64(6): 2036-2042.

[13] Kawahara A, Chung P M, Kawaji M.Investigation of two-phase flow pattern, void fraction and pressure drop in a microchannel [J].International Journal of Multiphase Flow, 2002, 28: 1411-1435.

[14] Saisorn S, Wongwises S.An experimental investigation of two-phase air-water flow through a horizontal circular micro-channel [J].Experimental Thermal and Fluid Science, 2009, 33: 306-315.

[15] Pansunee Suwankamnerd, Somchai Wongwises.An experimental study of two-phase air-water flow and heat transfer characteristics of segmented flow in a microchannel [J].Experimental Thermal and Fluid Science, 2015, 62: 29-39.

[16] Ma Youguang(马友光), Ji Xiyan(季喜燕), Zhu Chunying (朱春英).The influence of aspect ratios on void fraction of gas-liquid two-phase flow in microchannels [J].Chemical Engineering (China)(化学工程), 2010, 38(11): 35-38.

[17] Fukano T, Kariyasaki A.Characteristics of gas-liquid two-phase flow in capillary [J].Nuclear Engineering and Design, 1993, 141: 59-68.

[18] Zhou Yunlong(周云龙), Huang Na(黄娜).Numerical study on the flow characteristics of gas-liquid two-phase flow in horizontal square channel under microgravity [J].Proceedings of the CSEE(中国电机工程学报), 2014, 34(26): 4500-4507.

[19] Yao Chaoqun, Zhao Yuchao, Ye Chunbo, Dang Minhui, Dong Zhengya, Chen Guangwen.Characteristics of slug flow with inertial effects in a rectangular microchannel [J].Chemical Engineering Science, 2013, 95: 246-256.

[20] Xu J H, Li S W, Tan J, Luo G S.Correlations of droplet formation in T-junction microfluidic devices: from squeezing to dripping [J].Microfluidics and Nanofluidics, 2008, 5(6): 711-717.

[21] Kositanont C, Putivisutisak S, Tagawa T, Yamada H, Assabumrungrat S.Multiphase parallel flow stabilization in curved microchannel [J].Chemical Engineering Journal, 2014, 253: 332-340.

[22] Burns J R, Ramshaw C.Development of a microreactor for chemical production [J].Chemical Engineering Research and Design, 1999, 77(3): 206-211.

[23] Meng Meng(孟勐), Peng Xiaofeng(彭晓峰).Non-uniformity of flow boiling heat transfer on serpentine elbows [J].Journal of Engineering Thermophysics(工程热物理学报), 2009, 30(3): 498-500.

[24] Steinbrenner J E, Hidrovo C H, Wang F M, Vigneron S, Lee E S, Kramer T A, Cheng C H, Eaton J K, Goodson K E.Measurement and modeling of liquid film thickness evolution in stratified two phase microchannel flows [J].Applied Thermal Engineering, 2007, 27: 1722-1727.