液滴碰撞球形凹曲面复合level set-VOF法的数值分析

郑志伟，李大树，仇性启，朱晓丽，崔运静

（1 中国石油大学（华东）化学工程学院，山东 青岛 266555；2 中国石油大学（华东）机电工程学院，山东 青岛 266555）

引 言

液滴冲击壁面现象广泛存在于工业技术领域中，如喷雾冷却、喷雾干燥、旋风分离、喷雾燃烧等[1-3]。液滴撞壁是非线性、强瞬变过程，影响因素众多（如碰撞速度、液滴直径、壁面接触角等），而且各参数之间相互影响[4-5]，其中壁面结构，如水平壁面、倾斜壁面、与液滴直径同尺度的曲面等，对液滴的铺展、回缩、回弹有重要的影响。

近年来，研究者针对液滴撞壁现象进行了大量研究[1,6-10]。Rioboo 等[7]实验观测了液滴碰撞过程中瞬时飞溅、皇冠飞溅、回缩破碎及局部回弹等形态变化，Mao 等[8]实验研究了不同液滴碰撞不锈钢平面的铺展和回弹特性。实验研究集中在液滴撞壁形态变化及动力学行为（自由表面流动，气液固三相接触线运动）的观测上，难以揭示撞壁过程中液滴微细流动和破碎机理。数值模拟方面，Tabbara 等[9]采用流体体积（volume of fluid，VOF)法数值研究了不同碰撞速度的液滴冲击平面的铺展特性，高珊等[10]采用VOF 方法研究了液滴冲击壁面的流动和传热特性。上述文献虽对液滴撞壁过程进行了大量的研究，但对撞壁过程中液滴微细流动和破碎机理的揭示仍有不足。现有液滴撞壁的研究多集中在液滴冲击水平壁面，碰撞与液滴直径同尺度的曲面较为缺乏，而液滴曲面撞壁和液滴平面撞壁存在很大的不同。因此，本工作针对液滴碰撞球形凹曲面，采用复合水平集法（level-set）和VOF 法（couple level-set and volume of fluid，CLSVOF)[11-12]建立欧拉固定网格体系下的计算模型，对比CLSVOF 模型和VOF 模型计算精度，揭示液滴内部微细流动传热和破碎机理，开展液滴碰撞特性（铺展系数、铺展速度、射流长度和射流速度）的碰撞速度效应数值研究，并基于此对比分析现有液滴平面撞壁最大铺展系数理论解析模型，探索现有模型不足，提出液滴凹曲面撞壁最大铺展系数解析模型的发展 方向。

1 数值计算方法

1.1 数值计算模型

数值计算模型中液滴初始直径为D0=2 mm，以一定碰撞速度U0垂直冲击曲率为κ=0.2 mm-1的凹面，静态接触角θ=140°，如图1所示。其中，受实验条件限制，壁面静态接触角为实验测量平壁上平衡接触角，液滴和基板的温度与环境温度相同，都为300 K，环境压力为101.3 kPa（1 atm），计算所 需参数见表1。

图1 液滴凹面撞壁示意图及边界条件Fig.1 Computational domain and boundary conditions

考虑到液滴撞壁过程具有强瞬态变化的复杂拓扑结构，相界面的精确追踪是研究液滴撞壁现象的前提。目前应用最为广泛的相界面追踪技术主要是流体体积法（VOF）[13]和水平集法（level-set）[14]。VOF 法通过求解计算单元内相体积分数追踪相界面。该方法能够保证相界面处物理量守恒，但由于控制函数的不连续性，相界面计算精度与level-set法相比较低。level-set 法通过将相界面定义为水平集函数的零水平集并进行求解得到相界面。由于水平集函数是平滑连续的函数，相界面空间梯度能够精确计算，但该方法已被证明在计算过程中物理量不守恒[15]。为满足液滴撞壁过程中相界面空间梯度的精确求解和计算过程中物理量守恒，本工作采用CLSVOF 法建立液滴撞壁模型。

计算模型对控制方程进行求解，并做如下假设：气液界面无相变发生；碰撞过程一直处于层流状态。

在CLSVOF 模型中，连续性方程和N-S 方程分别为

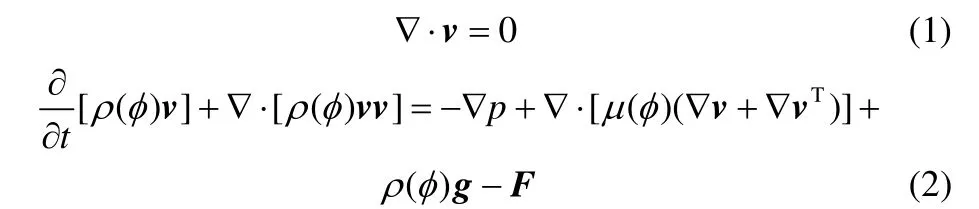
式中，v是速度矢量，p是压力，μ(φ)是计算单元内动力黏度，ρ(φ)是计算单元内密度，F是表面张力源项。

表面张力采用Brackbill 等[16]提出的连续表面力（CSF）模型求解，F可表示为

式中，κ是曲率，σ是表面张力系数，H是Heaviside 函数。

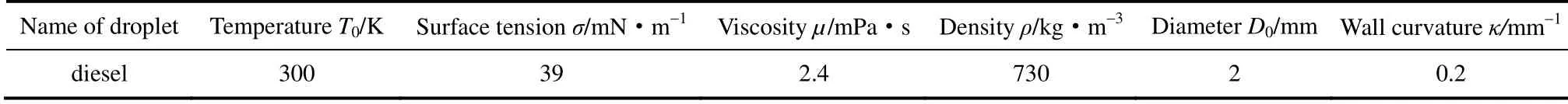
表1 计算参数Table 1 Calculation parameters

当液滴在壁面运动时，定义接触角为θ。nw和tw分别为单位法向向量和单位壁面切向量，则壁面的法向方向为

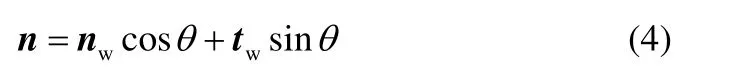
1.2 求解方法

计算采用二维轴对称模型，并采用网格加密技术对壁面附近区域进行加密，以提高计算精度。对网格进行无关性检验，分别采用每毫米20 个、30个、40 个网格的不同划分方式对计算区域进行划分，即网格尺寸分别是0.05、0.033、0.025 mm。结果表明，采用0.033 mm 和0.025 mm 的网格液滴撞壁后铺展因子随时间的变化曲线几乎完全重合，而0.05 mm 的网格与两者存在一定的差距。因此，本工作采用0.033 mm 的网格，既可保证计算精度，又可节省计算时间和成本，网格总数为180000 个。

采用有限体积法对控制方程进行离散。压力速度耦合采用SIMPLE 方法；压力求解采用PRESTO！方法；计算单元液相体积分数采用CICSAM[17]方法离散求解；控制方程采用QUICK 格式进行离散，以减少假扩散，提高精度；时间步长tΔ=10-6s，tΔ内迭代30 次内即可收敛。

2 计算模型验证

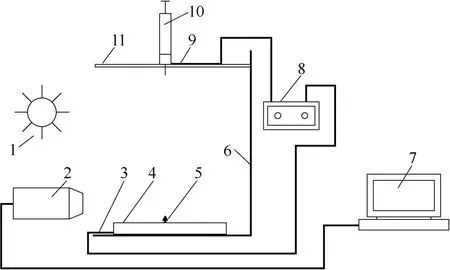
图2 实验装置Fig.2 Experimental system

本工作主要验证液滴撞壁模型中的相界面追踪模型、壁面润湿模型和流动模型。结合现有实验条件，本工作开展柴油液滴平面撞壁实验，对模型进行验证，实验系统如图2所示。实验采用德国Basler 公司A504KC 型数字面阵高速摄像仪对液滴撞壁的运动形态变化进行拍摄，结合图像处理软件 和像素分析方法进行数据分析。实验中，由注射器缓慢流出的液体在针尖处形成液滴，当液滴的重力大于其表面张力时，液滴从针头剥落。液滴的直径取决于所选用注射器针头的直径，并通过在高速摄像仪拍摄区域放置参照物（已知直径的刚性小球）进行标定。实验中，通过调整滑动支架的高度控制液滴的碰撞速度，液滴始终垂直碰撞壁面，本工作验证实验中碰撞速度U0=1.49 m·s-1，液滴初始直径D0=2.378 mm。

将数值结果与实验数据进行对比，如图3所示。可以看出，在液滴撞壁整个铺展阶段数值模拟和实验观测的液滴撞壁运动形态较为相似，如图3(a)所示。图3(b)将实验测量铺展系数f（f=Ds/D，Ds为液滴铺展直径）与模型计算所得f表示成量纲1 时间（t∗=tU/D）的函数[18]，可以看出数值模拟铺展系数与实验观测铺展系数呈现出相似的变化。其中，CLSVOF 模型与VOF 模型相比计算结果与实验观测值较为接近，说明CLSVOF 模型能够更好地模拟具有复杂强瞬变相界面拓扑结构的非线性、强瞬态的液滴撞壁过程，因此采用CLSVOF 法研究液滴碰撞特性更为精确可行。此外，现有数字图像处理技术和相界面追踪方法的局限性也是实验观测值和模拟结果存在偏差的原因。

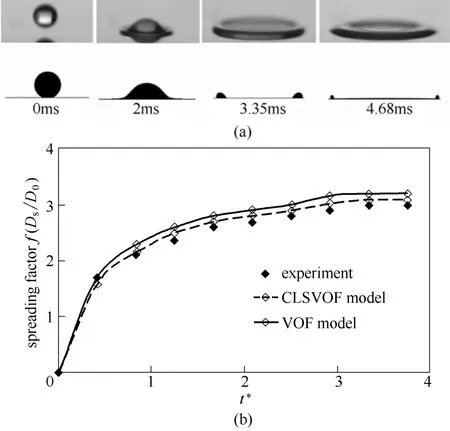
图3 实验和模拟结果对比Fig.3 Comparison of simulation with experiments

3 数值计算结果讨论

3.1 液滴的流动

为揭示液滴凹面撞壁微细流动机理，对直径D0=2 mm、碰撞速度U0=1.2 m·s-1的液滴不同碰撞时刻的压力、速度及温度分布进行分析，其中凹面的曲率为0.2 mm-1，如图4所示。可以看出，液滴在碰撞过程中受惯性力、黏滞力以及表面张力的共同作用，先后呈现出铺展、收缩及回弹形态。0.14 ms 时，液滴边缘B处压力最大（pB=2.42×103Pa），在惯性力的作用下B点获得了较大的铺展速度（UB=3.24 m·s-1），大约是碰撞速度U0=1.2 m·s-1的3倍。2.24 ms 时，液滴达到最大铺展直径，铺展边缘B处液体具有较大的压力梯度，开始回缩，pB受黏滞力、重力壁面切向分量和沿程阻力的共同作用而显著降低（pB=1.89×102Pa），UB沿壁面回流向碰撞中心A，UB=0.15 m·s-1。4.46 ms 时，液滴受表面张力和重力壁面切向分量主导，在碰撞中心A处形成回弹射流，A处具有较大的压力梯度（pA=2.62×102Pa)，从而A处获得了较大的射流速度（Ujet=0.4 m·s-1）。随着表面张力和重力壁面切向分量的作用逐渐增大，Ujet逐渐增大至3.2 m·s-1，回弹射流相应逐渐变长。

3.2 液滴飞溅破碎

液滴撞壁后，在较大的惯性力作用下铺展边缘容易产生破碎小液滴。本工作从涡量分布的角度揭示液滴边缘飞溅破碎机理，如图5所示。从图5(a)可以看出，0.1 ms 时，液滴三相接触线附近产生倾斜向上的射流，在射流的顶部区域受表面张力的作用呈球形，该区域具有复杂的表面张力作用。在上述表面张力的作用下射流颈部出现收缩现象，当颈部直径足够小时液滴会从射流破碎，向周围飞溅。上述现象可归结于Rayleigh 不稳定性的作用[3,5]。1.2 ms 时，在液滴铺展边缘存在破碎液滴群。由于破碎液滴群中的液滴受惯性力、黏性力、表面张力以及重力壁面切向分量作用的大小不同，靠近液滴主体的小液滴呈现出向铺展方向偏移的“倾斜液滴”，远离液滴主体的液滴则呈现出“半椭圆形液滴”。结合图5(b)的涡量分布，可以看出液滴铺展边缘和靠近液滴主体的小液滴间存在较大的涡量，说明空气对该区域的剪切作用较大。由于涡量的存在，液滴表面和液滴主体具有不同的压力，在此压力梯度的扰动下形成“卡门涡街”，加剧了液滴的破碎。

图4 液滴撞壁压力和速度分布Fig.4 Pressure and velocity distributions

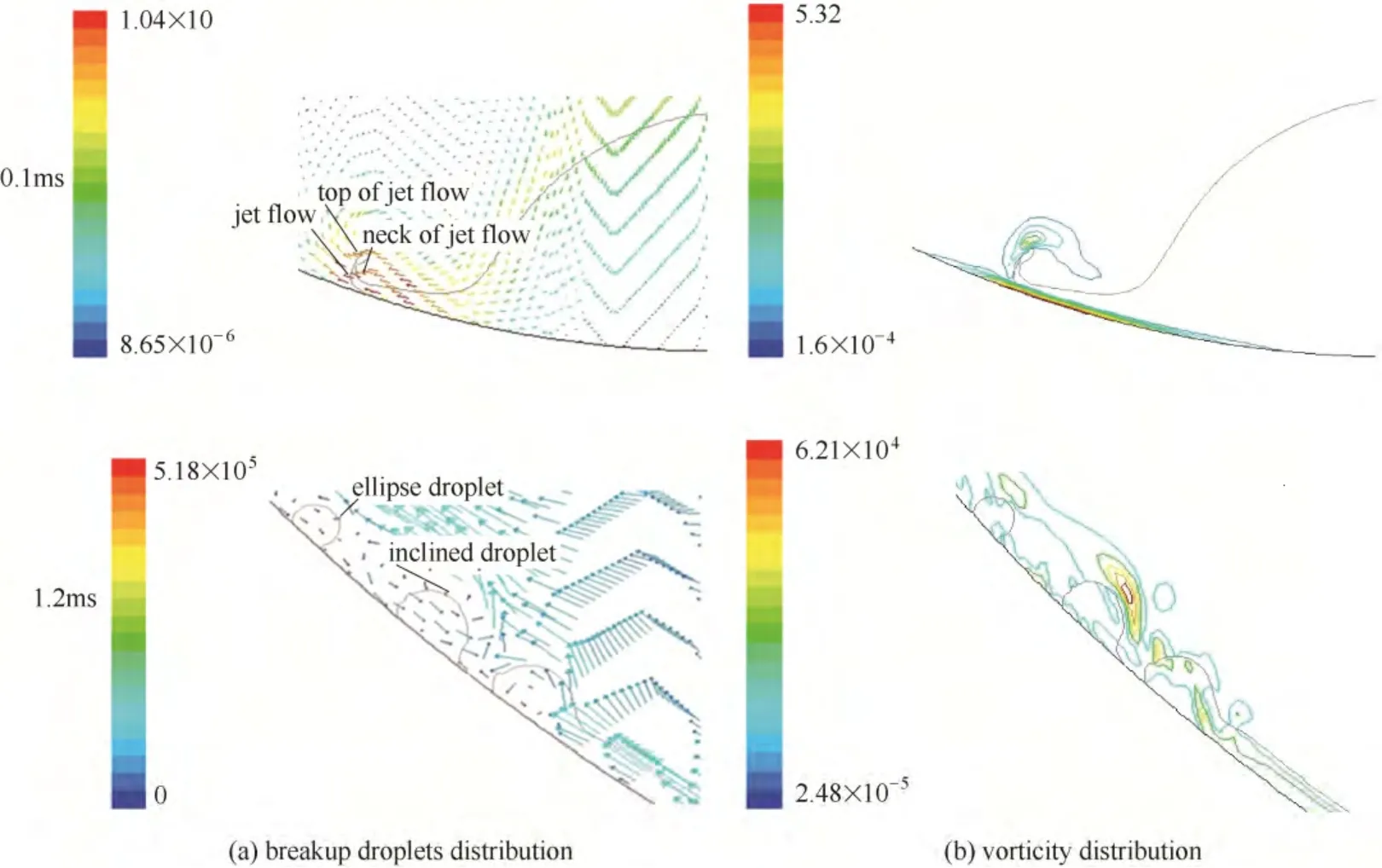
图5 碰撞过程破碎液滴和涡量分布Fig.5 Breakup droplets distribution and vorticity distributions

3.3 碰撞速度效应

由于液滴凹面撞壁受重力壁面切向分量和壁面结构影响，液滴的撞壁特性与平面撞壁相比存在较大的不同。为对比液滴碰撞不同壁面的撞壁特性，对直径D0=2 mm、碰撞速度U0=1.2 m·s-1的液滴进行平面撞壁模拟。同时，为分析液滴碰撞速度对凹面碰撞特性的影响，选取直径D0=2 mm，碰撞速度U0=1.2、2.5、3.5 m·s-1的液滴进行模拟。

图6为不同碰撞速度下液滴铺展系数f和铺展边缘B处铺展速度Us随时间的变化。从图6(a)可以看出，f随碰撞速度增加而变大，而且液滴碰撞速度越大，液滴达到最大铺展系数fmax所需时间越短，fmax分别为1.1、1.5 和1.73。从图6(a)还可以看出，液滴达到最大铺展系数所需时间几乎相同，但平面撞壁的铺展系数为2.3，大于凹面撞壁的1.1，可见凹面撞壁过程中重力壁面切向分量对液滴撞壁特性的影响较大。从图6(b)可以看出，液滴碰撞速度越大，铺展速度越大，不同碰撞速度下的液滴铺展速度的变化呈现出相似的变化规律：液滴的铺展速度随时间逐渐减小；液滴最大铺展速度出现在撞壁初始时刻，Us分别为2.998、6.23 和10.2 m·s-1，大于相对应的液滴碰撞速度U0分别为1.2、2.5 和3.5 m·s-1。这是由于液滴与壁面接触时液滴的动 量由轴向全部转换为径向，因此在撞壁初始时刻液滴具有较大的铺展速度。碰撞速度较大的液滴具有较大的惯性势能，其铺展速度也较大。随着液滴沿壁面铺展，受黏滞力、表面张力和重力壁面切向分量的共同作用，惯性力的作用逐渐减小，铺展速度逐渐减小，当液滴达到最大铺展直径时液滴的铺展速度减小为0。液滴的碰撞速度越大，其铺展系数越大，铺展初始阶段的铺展速度越大。从图6(b)还可以看出，相同直径和碰撞速度的液滴碰撞平面和凹面，其铺展速度十分接近。

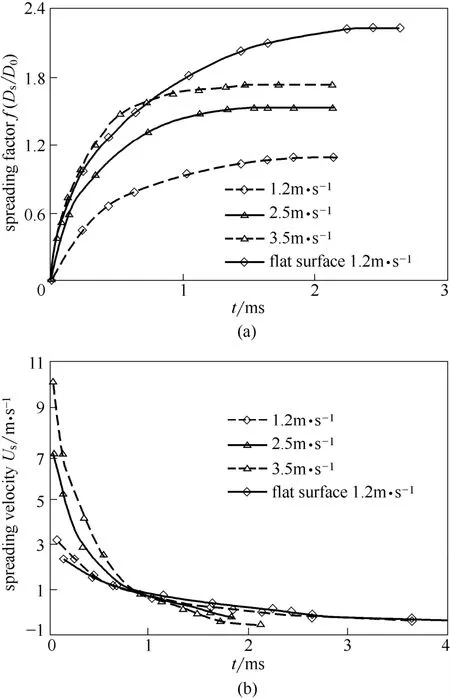
图6 不同碰撞速度下液滴铺展系数和铺展速度随时间的变化Fig.6 Spreading factor and velocity change with time at different impact velocities

为研究液滴的回弹特性，图7为液滴相对回弹射流长度δ（δl/D0，δl是射流长度）和射流速度Ujet随时间的发展。其中，液滴的相对回弹射流长度为液滴碰撞中心A处液膜的厚度，射流速度为液滴射流前端最大速度。图7中的射流长度和射流速度从液滴达到最大铺展系数时刻开始选取。可以看出，液滴碰撞速度越大，回弹射流发展越充分，回弹射流越长，在中心射流离开壁面前最大射流长度分别为4.36、7.27、8.5 mm；液滴的回弹射流速度随碰撞速度增加而增大，分别为3.6、4.95、5.275 m·s-1，大于其对应时刻的碰撞速度U0分别为1.2、2.5 和3.5 m·s-1。不同碰撞速度下的δ和Ujet呈现出相似 的变化规律：液滴到达最大铺展直径后，液滴铺展外缘处的液体受表面张力和重力壁面的主导开始回缩，但碰撞中心处液体受惯性力主导继续铺展，因此，在液滴沿壁面回缩初始阶段可见碰撞中心处的液膜速度垂直向下，液膜厚度逐渐减小为0；之后，由于表面张力和重力壁面切向分量的作用随边缘液体的回缩逐渐增大，碰撞中心处的液体逐渐回弹，射流速度垂直向上迅速增大，形成射流。此外，图7通过对比相同直径以及相同碰撞速度的液滴碰撞平面和凹面可知，液滴平面撞壁的回弹射流出现时间滞后于凹面撞壁，而且回弹射流速度大于凹面撞壁，再次证明了重力壁面切向分量对液滴凹面撞壁特性的影响较大。

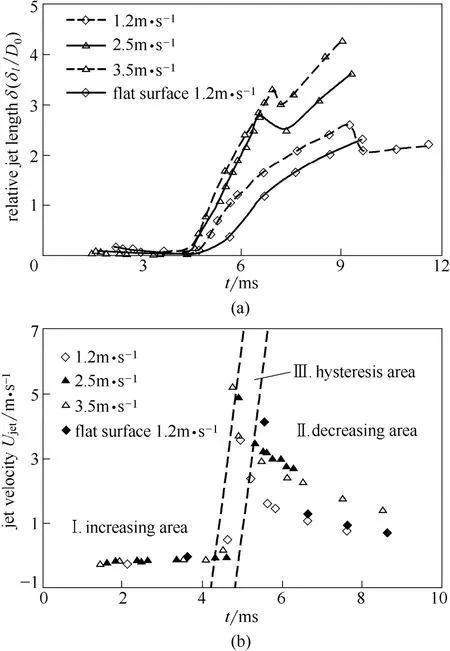
图7 不同碰撞速度下液滴射流长度和射流速度随时间的变化Fig.7 Jet and velocity change with time at different impact velocities

图8是液滴的最大铺展系数fmax随Reynolds 数Re的变化。可以看出，液滴的Re越大，其fmax越大。需要指出，液滴的fmax在较小的Re下增幅较大，当Re取值约为2100 时fmax增幅明显减小。将fmax拟合成Re的函数可得

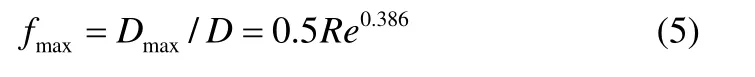
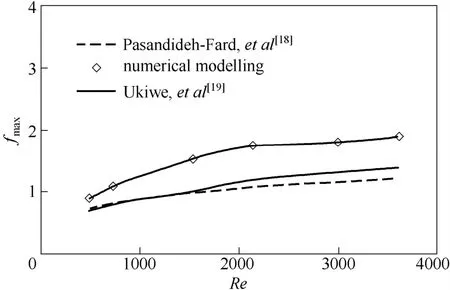
图8 最大铺展系数随Re 的变化Fig.8 Maximum spreading factor changes with Re

为分析液滴铺展速度Us、射流长度δ和射流速度Ujet与Reynolds 数的关系，得到不同Re下液滴相对最大铺展速度（U′s/U′0，U′s为最大铺展速度）、相对最大射流长度（δ′/D0，δ′为最大铺展速度）和相对最大射流速度（U′jet/U′0，U′jet为最大射流速度)的变化规律，如图9所示。可以看出，液滴的相对最大铺展速度随Re的增加而增大，液滴的相对最大射流速度随Re的增加而减小。当液滴的Re取值约为2100 时，液滴的相对最大铺展速度和相对最大射流速度逐渐趋于稳定，与液滴Reynolds 数的相关性逐渐减小，碰撞速度效应逐渐减小。将液滴的相对最大铺展速度和相对最大射流速度拟合成Re的函数可得

从图9还可以看出，液滴相对最大射流长度随Reynolds 数增加而增加，当Re取值约为2100 时增幅明显减小。这说明，随着液滴Reynolds 数的不断增加，液滴相对最大射流长度与液滴Reynolds 数相关性逐渐减小，液滴碰撞特性碰撞速度效应逐渐减小。将相对最大射流长度拟合成Re的函数可得

图9 量纲1 速度和相对射流长度随Re 的变化Fig.9 Dimensionless velocity and relative jet velocity change with Re

液滴的铺展系数和铺展速度与Reynolds 数的相关性随Re的增加逐渐减小。分析认为，这是由于，Reynolds 数越大，液滴的惯性势能的作用越明显，较大的惯性势能一部分转化成克服黏性耗散的铺展势能，另一部分转化成克服表面张力做功的飞溅势能。当Reynolds 数足够大时，由于液滴撞壁过程中黏性耗散随Reynolds 数的变化不大，液滴所具有的铺展势能也较为接近，液滴的铺展系数和铺展速度与Reynolds 数的相关性明显减小。而液滴的射流长度和射流速度与Reynolds 数的相关性随Re的增加逐渐减小。分析认为，这是由于，液滴的收缩势能与冲击动能有关，当Reynolds 数较小时，液滴的收缩势能随Reynolds 数的增加逐渐增大，因此射流长度和射流速度与Reynolds 数的相关性较大。而液滴的收缩势能还与液滴铺展势能和表面张力做功密切相关，当Reynolds 数足够大时，液滴的铺展势能和表面张力做功的能力几乎不变，因此液滴的射流长度和射流速度与Reynolds 数的相关性明显减小。

液滴碰撞固体壁面的最大铺展系数是液滴撞壁过程中的重要特性参数，而现有理论解析模型多针对液滴的平面撞壁[18-20]。本工作通过将现有液滴平面撞壁最大铺展系数理论解析模型与数值模型对比，提出液滴凹曲面撞壁最大铺展系数解析模型发展方向。根据研究方法的不同，液滴最大铺展系数理论解析模型可以分为两大类：流体力学法和质量守恒法。由于流体力学法在推导过程中做出大量假设，基于能量守恒方程建立液滴最大铺展系数理论解析模型更为准确。

液滴碰撞过程能量主要包括液滴碰撞前动量E1、碰撞前表面能ES1、碰撞后表面能ES2、黏性耗散能W，即

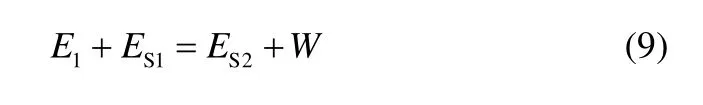
其中

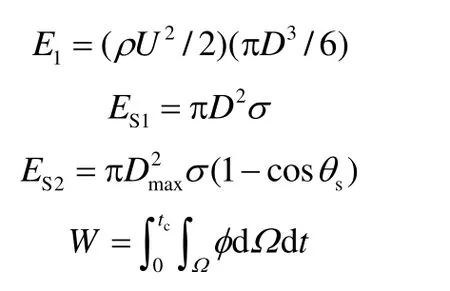
式中，Dmax是液滴最大铺展直径，θs是平衡接触角，tc是液滴达到最大铺展直径所需时间。

Pasandideh-Fard 等[18]、Ukiwe 等[19]根据质量守恒定律，采用不同的能量耗散方程分别建立了液滴平面撞壁最大铺展系数解析模型。图8将不同Reynolds 数下数值模拟液滴最大铺展系数与上述解析模型进行对比，可以看出Pasandideh-Fard 等、Ukiwe 等所建立的模型解析解略高于数值模拟结果，这是由于文献中解析模型假设液滴以圆柱形态进行铺展，这与凹面撞壁液滴形态变化相差较大。当液滴的Re较小时，数值模拟结果与文献中解析模型计算值较为接近，这是由于碰撞速度较小的液滴铺展系数较小，沉积液膜厚度较大，液滴铺展形态接近于圆柱形。而当液滴的Re较大时，由于碰撞速度较大的液滴具有较大的铺展直径和较小的沉积液膜厚度，液滴铺展形态近似呈贴壁碗状，数值模拟结果与文献中解析模型计算值相差较大。此外，文献[3]分析认为理论解析值与数值计算结果略有偏差主要还有两个原因：解析模型求解黏性耗散能没有考虑热量传递对流动边界层厚度的影响，模型流动边界层厚度取流动滞止条件下边界层厚度；碰撞基板为表面固体结构分数很小的疏油不锈钢板，因此结构表面的黏性耗散可以忽略，但结构表面内侵入流体的黏性耗散则需要考虑。由此可见，液滴沉积形态的精确近似、流动边界层的精确选取以及结构表面内黏性耗散的精确计算是液滴凹面撞壁最大铺展直径理论解析模型发展的一个方向。

4 结 论

采用CLSVOF 方法建立了数值计算模型，以探索液滴撞壁机理及特性。本工作揭示了液滴撞壁流动和破碎机理，获得了碰撞速度对液滴的铺展系数、铺展速度、回弹射流长度和射流速度的影响规律，并提出了液滴最大铺展系数理论解析模型的发展方向，具体结论如下。

（1）CLSVOF 方法与VOF 方法相比，能够更好地预测具有复杂相界面拓扑结构变化的非线性、强瞬态的液滴撞壁过程。

（2）受惯性力、黏滞力、表面张力和重力壁面切向分量以及凹面结构的共同作用，液滴碰撞凹面过程先后呈现出铺展、收缩、振动及回弹状态；液滴破碎是由于Rayleigh 不稳定性作用；空气流经破碎液滴产生“卡门涡街”现象，从而加剧了液滴破碎。

（3）液滴的撞壁特性与液滴碰撞速度密切相关。液滴凹曲面撞壁与平面撞壁相比，铺展系数较小，回弹射流出现的时间超前，回弹射流速度较大。液滴凹面撞壁是否回弹与碰撞速度不相关（23.9＜We＜1320）；液滴的最大铺展系数和相对最大铺展速度与Reynolds 数近似幂递增，液滴的相对最大射流长度与Reynolds 数近似对数递增，液滴的相对最大射流速度与 Reynolds 数近似幂递减，但当Reynolds 数取值约为2100 时碰撞速度效应逐渐 减小。

符 号 说 明

D——液滴直径，mm

E1，ES1，ES2——分别为碰撞前动量、碰撞前表面能、碰撞后表面能，J

F——表面张力源项

f——铺展系数

H——Heaviside 函数

nw——单位法向向量

P——压力，Pa

tw——单位壁面切向量

U——速度，m·s-1

W——黏性耗散能，J

δ——相对回弹射流长度

θ——接触角，（°）

κ——曲率

µ——黏度，Pa·s

v——速度矢量

ρ——密度，kg·m-3

σ——表面张力系数，N·m-1

下角标

jet——射流

s——铺展状态

0——初始状态

[1]Yang Baohai (杨宝海),Wang Hong (王宏),Zhu Xun (朱恂),et al.Effect of velocity on behavior of droplet impacting superhydrophobic surface [J].CIESC Journal(化工学报),2012,63 (10):3027-3033

[2]Moreira A L N,Moita A S,Panao M R.Advances and challenges in explaining fuel spray impingement:how much of single droplet impact research is useful? [J].Progress in Energy and Combustion Science,2010,36 (5):554-580

[3]Li Dashu (李大树),Qiu Xingqi (仇性启),Cui Yunjing (崔运静),et al.Numerical analysis on impacting velocity effect on spray oil droplet impacting onto a surface during diesel engine cold starting [J].Transactions of the Chinese Society for Agricultural Machinery(农业机械学报),2014,45 (6):25-31

[4]Liang Chao (梁超),Wang Hong (王宏),Zhu Xun (朱恂),et al.Numerical simulation of droplet impact on surfaces with different wettabilities [J].CIESC Journal(化工学报),2013,64 (8):2745-2751

[5]Li Dashu (李大树),Qiu Xingqi (仇性启),Yu Lei (于磊),et al.Review of spray droplet impact on a surface [J].Industrial Heating(工业加热),2014,43 (2):1-4

[6]Ge Y,Fan L S.Droplet-particle collision mechanics with film-boiling evaporation [J].Journal of Fluid Mechanics,2007,573:311-337

[7]Rioboo R,Tropea C,Marengo M.Outcomes from a drop impact on solid surfaces [J].Atomization and Sprays,2001,11 (2):155-65

[8]Mao T,Kuhn D,Tran H.Spread and rebound of liquid droplets upon impact on flat surfaces [J].AIChE Journal,1997,43 (9):2169-2179

[9]Tabbara H,Gu S.Modelling of impingement phenomena for molten metallic droplets with low to high velocities [J].International Journal of Heat and Mass Transfer,2012,55 (7):2081-2086

[10]Gao Shan (高珊),Qu Wei (曲伟),Yao Wei (姚伟).Flow and heat transfer of droplet impinging on hot flat surface during spray cooling [J].Journal of Engineering Thermophysics(工程热物理学报),2007,28 (1):221-224

[11]Sussman M,Puckett E G.A coupled level set and volume-of-fluid method for computing 3D and axisymmetric incompressible two-phase flows [J].Journal of Computational Physics,2000,162 (2):301-337

[12]Yokoi K.A numerical method for free-surface flows and its application to droplet impact on a thin liquid layer[J].Journal of Scientific Computing,2008,35(2/3):372-396

[13]Hirt C W,Nichols B D.Volume of fluid (VOF) method for the dynamics of free boundaries [J].Journal of Computational Physics,1981,39 (1):201-225

[14]Tanguy S,Berlemont A.Application of a level set method for simulation of droplet collisions [J].International Journal of Multiphase Flow,2005,31 (9):1015-1035

[15]Olsson E,Kreiss G.A conservative level set method for two-phase flow [J].Journal of Computational Physics,2005,210 (1):225-246

[16]Brackbill J U,Kothe D B.A continuum method for modeling surface tension [J].Journal of Computational Physics,1992,100 (2):335-354

[17]Ubbink O,Issa R I.A method for capturing sharp fluid interfaces on arbitrary meshes [J].Journal of Computational Physics,1999,153 (1):26-50

[18]Pasandideh-Fard M,Qiao Y M,Chandra S,Mostaghimi J.Capillary effects during droplet impact on a solid surface [J].Phys.Fluids,1996,8:650-659

[19]Ukiwe C,Kwok D Y.On the maximum spreading diamater of impacting droplets on well-prepared solid surfaces [J].Langmuir,2005,21:666-673

[20]Chandra S,Avedisian C T.On the collision of a droplet with a solid surface [J].Proceedings of the Royal Society of London.Series A:Mathematical and Physical Sciences,1991,432 (1884):13-41