十字交叉微通道内微液滴生成过程的数值模拟

王维萌，马一萍，陈斌

（西安交通大学动力工程多相流国家重点实验室，陕西 西安 710049）

引 言

近年来，以微流控芯片为基础、以操纵微小液滴为手段的微液滴微流控技术发展迅猛，在石油化工、日用医药、环境科学以及化学分析等领域得到了广泛应用[1-2]。微液滴的制备是操控微液滴的前提，利用微通道特殊结构来制备微液滴的方式主要包括T/Y 型交错通道、二维对称流动聚焦通道、三维轴对称共轴聚焦通道[3]以及其他类型如阶梯型微通道[4]等。其中，流动聚焦微通道生成的微液滴尺寸范围较广、大小可控、单分散性较好，且对壁面材料润湿性要求不高而受到人们的关注。

目前，许多研究人员通过实验研究和数值模拟方法对微通道内液液、气液流型以及相关影响因素进行了大量的研究，并且尝试建立一系列理论和模型来预测其各种动力学行为。在实验方面，Umbanhowar 等[5]首先将共轴流动聚焦微通道引入液液两相系统，然后Anna 等[6]与Dreyfus 等[7]将这种三维共轴流动装置改造成一类准二维平面流动聚焦装置，他们发现利用流动聚焦结构微通道生成的微液滴尺寸与通道交叉下游处所设置的狭窄孔道和两相流速有关。Garstecki 等[8]利用十字聚焦微流控装置生成了单分散气泡，其尺寸分布从10 μm 到1000 μm 不等；Takeuchi 等[9]设计制造了一种结构简单、尺寸较小的圆形通道流动聚焦装置。Yobas等[10]和Ong 等[11]应用更加复杂的微制造技术在流动聚焦装置通道交叉处加工了一个圆形孔，从而能够生成尺寸更小、频率更高的微液滴。Wang 等[12]和Young 等[13]将流动聚焦装置并列线性整合以提高微液滴产率。Nisisako 等[14]则将聚焦微流控装置类似于T 型微通道般环形布置以提高产率。Funfschilling 等[15]利用micro-PIV 对连续相流体内形成的离散相液体进行测量，获得了流场信息从而支持了拉伸挤压-剪断理论。Zhou 等[16]认为离散相夹断生成微液滴的机理在两种流型中均适用。Cubaud 等[17]发现在十字聚焦流动装置中微液滴尺寸在射流流型中只与两相流速比有关，而在滴状流型中则与连续相Ca数有关。在模拟方面，Liu 等[18]同样采用三维lattice Boltzmann 方法来模拟低连续相Ca数下十字聚焦微通道中微液滴的生成，依据连续相Ca数和两相流量的变化观测到了滴状流、射流及延展流3 种不同流型并绘制流型图来进行区分。Chen 等[19]利用三维VOF 方法对微通道内生成Taylor 气泡进行数值模拟，研究了挤压流型和剪切流型的形成机制，并获得了两种流型的转变临界毛细数。Sur 等[20]采用VOF 方法模拟了十字聚焦微通道中气液两相流型，分析了惯性力、黏性剪切力及两相表面张力对不同流型下微气泡形成的作用。Kim 等[21]利用lattice Boltzmann 方法对十字聚焦微通道内的油水两相流动形成微液滴进行了数值模拟，发现了水相液滴形成、发展以及最终分离的过程受到界面水动力不稳定性的影响。王澎等[22]采用VOF 方法模拟了T 型微通道内微液滴的破裂，提出了不同的破裂流型。

截至目前，有关十字聚焦微通道内液液两相生成微液滴的研究还停留在通过可视化实验观察流型的阶段，在通过三维数值模拟研究不同因素对液滴生成的大小和频率的影响方面较为欠缺。本文采用Fluent软件的VOF模型对十字交叉微通道内的微液滴形成过程进行三维数值模拟，同时通过可视化实验进行模型验证。在获得了不同的微液滴生成机理后，分析液液两相流速、表面张力系数、连续相黏度、界面接触角等因素对微液滴生成的影响，为实际应用提供指导。

1 物理模型及数值算法

1.1 控制方程及表面张力模型

在微尺度条件下，液液两相流速较低，因此可将液液两相均视作不可压缩黏性流体。Fluent 中的VOF模型基于有限体积法求解N-S方程，凌志勇等[23]的研究表明，在微米尺度下，重力对流动的流量与速度的影响很小，可以忽略不计，因此，连续性和动量方程可简化为

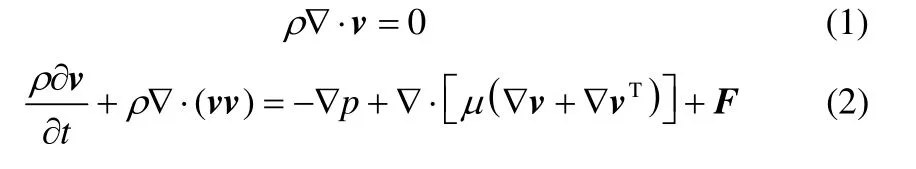
式中，F是表面张力源项，只存在于包含界面的控制单元内。VOF 模型通过引入流体体积函数α来计算各网格单元内两相的体积分数，从而捕捉液液相界面。以油水两相流动为例（o 和w 分别代表油和水），αw=1（αo=0）表示该控制体积全部被水相占据；αw=0（αo=1）表示该控制体积全部被油相占据；0＜αw＜1 表示油水相界面存在于该控制体积中，在此控制体积内式(1)、式(2)中的密度和黏度等参数皆以两相体积平均值进行计算，如式(3)、式(4)所示

VOF 模型中体积分数α的扩散方程求解其变化，以水相为例

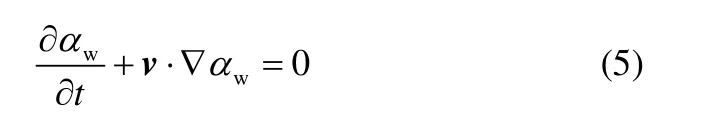
在VOF 模型中采用连续表面力模型（CSF）模拟微尺度条件下表面张力的作用，即式(2)中的 源项

式中，γ为两相表面张力系数；κw为界面曲率。可以通过对相界面单位法向量求散度获得

在远离壁面的计算网格单元内，可对水相体积分数αw取梯度来求出相界面单位法向量。即

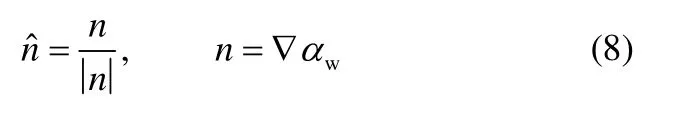
在邻近壁面的计算网格内，油水两相以固定的角度和壁面接触，可用接触角模型来表征壁面润湿性的影响。接触角θW可定义为在固壁面、油相及水相三者交界面处，油水两相相界面与固液（指定相，这里为水相）相界面的夹角。在该模型中贴近壁面的计算单元内单位法向量可由式(9)处理得到

式中，和分别代表壁面单位法向量以及切向量。

在本文数值模拟中，油和水分别设置为第1 相和第2 相。接触角设为180°，表明水相无法湿润壁面而油相可以完全湿润壁面，以符合实验中的PDMS 材料微通道壁面的疏水特性。

1.2 十字交叉微通道的结构以及尺寸

如图1所示，十字交叉微通道的水平段与垂直段横截面皆为矩形，通道尺寸可由HD、WD、HC、WC4 个参数来定义。HD和WD分别代表水平管道的高和宽度，HC、WC分别代表连续相入流段垂直管道的高和宽度。经过计算验证，连续相和离散相入流段管道长度超过3 倍管道宽度时不会影响模拟结果；水平通道在十字交叉区域后部的两相混合流动直管段长度为50WD。

图1 十字交叉微通道的三维几何结构及尺寸Fig.1 Three dimensional geometry and size of cross focusing micro-channel

图2 网格独立性验证（Ud=Uc=0.01 m·s-1）Fig.2 Grid independence verification（Ud=Uc=0.01 m·s-1）

液滴的大小由液滴在管道中心对称平面上的最大长度D表示，如图1(b)所示。三维十字交叉微 通道均使用正六面体网格进行划分，为了消除网格密度对模拟结果造成的影响，进行网格独立性检验。当Uc=Ud=0.01 m·s-1，液滴的量纲1 尺寸D/W随网格数的变化关系如图2所示，由图可知，网格数大于320000 时，D/W的模拟值随着网格数的增加几乎不再发生变化。网格数从320000 增加到400000时，D/W减少了0.63%，可以认为网格数为320000的数值模拟为网格无关性解。

1.3 参数设置

本文的数值计算和可视化实验中，以硅油为连续相，蒸馏水（添加酒精可改变黏度）作为离散相。假设流动的初始时刻通道内全部充满硅油，从t=0时刻，油和水分别以固定的流速Uc和Ud从两相入口流入。计算具体工况见表1。

几何界面重构方案采用PLIC 算法，压力速度耦合采用PISO 算法从而在求解瞬态流动时能够增大欠松驰因子的值而不影响解的稳定，压力差值方案选用PRESTO！算法，时间离散方式为一阶隐式格式，动量方程离散方式为二阶迎风差分格式。时间步长、Courant 数、亚松驰迭代因子等参数的选取在计算过程中根据计算结果的稳定性及收敛性选取。

表1 工质物性Table 1 Physical properties of working fluids

图3 数值模拟所得流型与实验结果的对比Fig.3 Comparison of flow patterns between numerical simulation and experimental observation

2 模型的有效性验证

为了验证模型的有效性，本文以蒸馏水（加入质量分数0.5%的SDS 作为表面活性剂）和硅油分别作为离散相和连续相流体工质，在截面尺寸为200 μm×100 μm 的十字交叉微通道内开展可视化实验研究，并将拍摄流型与数值模拟结果作对比验证。离散相流量为200～15000 μl·h-1，连续相流量为100～20000 μl·h-1。在上述条件下，得到了拉伸挤压流型、滴状剪切流型、单分散射流流型、紊乱射流流型、管状流型、滑移流型以及节状形变流型。对比结果如图3所示，数值模拟与实验结果吻合很好，验证了本文数值模拟方法的有效性。

对于能够生成单分散微液滴的拉伸挤压和滴状剪切流型，前人研究较多；对于射流，本文以是否能够产生单分散微液滴为判据，提出射流可分为单分散和紊乱两种流型。当两相流速较小时，微液滴以拉伸挤压模式生成[图3(a)]。随着连续相流速的增大，流型依次转变为滴状剪切[图3(b)]和单分散射流[图3(c)]。当提高离散相流速后，射流中的单分散射流逐渐消失，完全变为紊乱射流[图3(d)]。继续增大离散相流速，离散相在通道中形成较粗的变形液柱，而且液柱的直径发生周期性的变化，每隔一段距离会有一个直径很小的节点，这些节点将液柱分为了许多长度相等的液段，这时单分散微液滴已经无法产生，称这种流型为节状形变流[图3(e)]。继续增大离散相流速，会产生环状流型，并根据离散相液柱的粗细分为管状流[图3(f)]和滑移流[图3(g)]。当离散相流速继续加大，液液两相流型完全变为环状流型。

为了衡量液滴的大小和形状，本文采用液滴在微通道对称平面的轴向最长距离D和截面宽度W之比来定义液滴的量纲1 尺寸。当D/W＞1 时，由拉伸挤压模式形成的液滴将充满整个十字交叉后部水平两相汇聚通道并且与壁面相接触（液滴与壁面之间会形成一层较薄的液膜），此时液滴的形状由于受到壁面限制而形成弹状；当D/W≤1 时，液滴的生成过程可能处于滴状剪切或射流模式，并且随着连续相毛细数Ca的增大，液滴尺寸越小形状越接近球形。

式中，μc为连续相黏度，Uc为连续相速度；σ为两相表面张力。

图4给出了模拟中在拉伸挤压流型、滴状剪切流型和单分散射流流型的工况范围内D/W随连续相Ca数的变化关系，并与实验结果做了比较，两者吻合较好。从图中可以看出，液滴量纲1 尺寸随连续相Ca数的变化趋势随流型的变化而不同。当连续相Ca数减小时，微液滴的尺寸减小。但在拉伸挤压和滴状剪切流型下，微液滴尺寸的减小速率较大；当进入射流时，D/W的值趋向平坦，变化不大。另外，虽然D/W的值为1 是拉伸挤压和滴状剪切流型的分界线，但D/W值变化趋势减缓的拐点连续相Ca数大约为0.1，两者并不对应。因此，该拐点并非是拉伸挤压向滴状剪切模式变化的转折点。也就是说明在两者的过渡阶段，压力与剪切力的变化共同对微液滴的生成起作用。

图4 液滴量纲1 尺寸随连续相Ca 数的变化Fig.4 Dimensionless droplet size with respect to Ca number of continuous phase

3 结果与讨论

3.1 微液滴的生成机制以及流型

根据大量的实验和数值模拟可看出，随着液液两相工质物性、流动参数以及装置的结构和尺寸的变化，十字交叉微通道中液液两相流型主要表现为拉伸挤压（squeezing）、滴状剪切（dripping）、射流（jetting）以及各种不生成微液滴的类环状流型，如节状形变流（nodular flow）、管状流（turbulent flow）和滑移流（slip flow）。其中，拉伸挤压、滴状剪切和射流中的单分散射流这3 种流型能够产生具有高度单分散尺寸的微液滴。本文以数值模拟方法得到了这3 种不同的微液滴形成方式，并对这3种单分散生成方式形成微液滴的尺寸分布、形态、频率、稳定性等影响因素进行分析。

图5 典型的单分散微液滴生成机制Fig.5 Generation mechanism of typical jetting pattern

总之，十字交叉微通道内微液滴的生成过程基本上可以分为3 步：离散相液滴的隆起形成、液滴的长大、液滴与离散相的分离。但由于各流型工况的不同，每种流型产生液滴的过程又各有不同。如图5所示，拉伸挤压流型发生在较低的连续相Ca数下。此时离散相流体首先向下游延展，逐渐进入并充满水平段通道后部的两相汇聚部分，使得液液相界面沿水平通道下游方向积累产生较大的压差。这时离散相流体在下游通道内被连续相流体挤压并在交叉管道处发生颈缩，而且由于以上挤压过程慢于界面自由能的释放过程，因此这种离散相液体的挤压颈缩变形是一种平衡态过程。最终，当颈缩达到一定程度时，液滴在非稳态过程下快速脱离离散相流体并随着连续相流体沿汇聚通道向下游流动，而离散相流体的前端界面则返回两相管道交界处，重新开始以上过程。此流型表面张力起到了支配性的作用。对于滴状剪切流型，液滴的破裂是由于Rayleigh 毛细不稳定性造成的。该流型下离散相流体的界面前端延展并保持在两相管道交叉处。此时由于连续相Ca数较大，连续相的黏性剪切力作用起支配作用，所以离散相流体未充分进入两相汇聚通道就被两侧的连续相流体剪切带走，而且每个液滴破裂形成后，离散相界面前端没有收缩回流现象，而是生成细长的颈部。该流型产生时所处的毛细数区域要高于拉伸挤压流型，但生成液滴的尺寸较小。

随着连续相毛细数的继续增加，流型将转变为射流流型。该流型液滴的破裂机制仍然由Rayleigh毛细不稳定性造成，但却不易控制。一般离散相进入两相汇聚通道的距离在1 个通道宽度以上，而且离散相界面前端在两相汇聚通道内延伸得很远并保持成长液柱的形式，在长液柱的前端由于界面张力作用下逐渐隆起成球形，随着前端隆起的增大，连续相对其剪切作用也愈大，最终断裂形成液滴，并且后部形成许多很小的液滴。该流型生成的液滴尺寸与滴状剪切流型相比略小，但尺寸分布的单分散性随着该流型连续相Ca数的增大而变差，因此可按液滴尺寸分布是否具有单分散性来将射流分成单分散型射流和紊乱型射流。在该流型中，连续相的黏性剪切力与离散相的惯性力以及表面张力共同对流动产生作用。

3.2 液液两相流量对微液滴生成的影响

本节对表观速度在0.001～1 m·s-1范围内的液液两相流动工况进行数值模拟，获得了具有单分散性和稳定生成频率的微液滴。图6中展示了固定离散相流速下（µd=0.005 Pa·s，µc=0.056 Pa·s，σ=0.03 N·m-1），微液滴相对尺寸D/W与生成频率随两相流速比的变化情况。从图中可发现，当两相流速均较低时，微液滴主要以拉伸挤压状流型生成，随着连续相流速增大，微液滴生成机制逐渐转变为滴状剪切流型，随后变为单分散射流，最后转变为紊乱射流。在此过程中，微液滴的尺寸逐渐变小，生成频率逐渐增大。随着连续相流速的增大，微液滴尺寸减小趋势变缓，而微液滴生成频率增加趋势却变快。Fu 等[24-25]对于在十字聚焦微通道中气泡的生成提出过相似的结论，魏丽娟等[26]对于T 型微通道内液滴的生成也有相似结论，即随着连续相流速的增加，气泡的尺寸逐渐变小，生成频率逐渐变大，Xu 等[27]提出的T 型通道中液滴生成大小的关系式也验证了本文结论的正确性。另外，对于离散相流速来说，发现相同流速比下，随着离散相流速的增加，液滴的生成尺寸降低速率以及生成频率的增加速率变高，而且当离散相流速大于0.03 m·s-1时，微液滴的生成全部以射流形式进行。

3.3 两相表面张力对微液滴生成的影响

图6 液滴尺寸与频率随两相流速的变化Fig.6 Droplet size and frequency with respect to two-phase flow rates

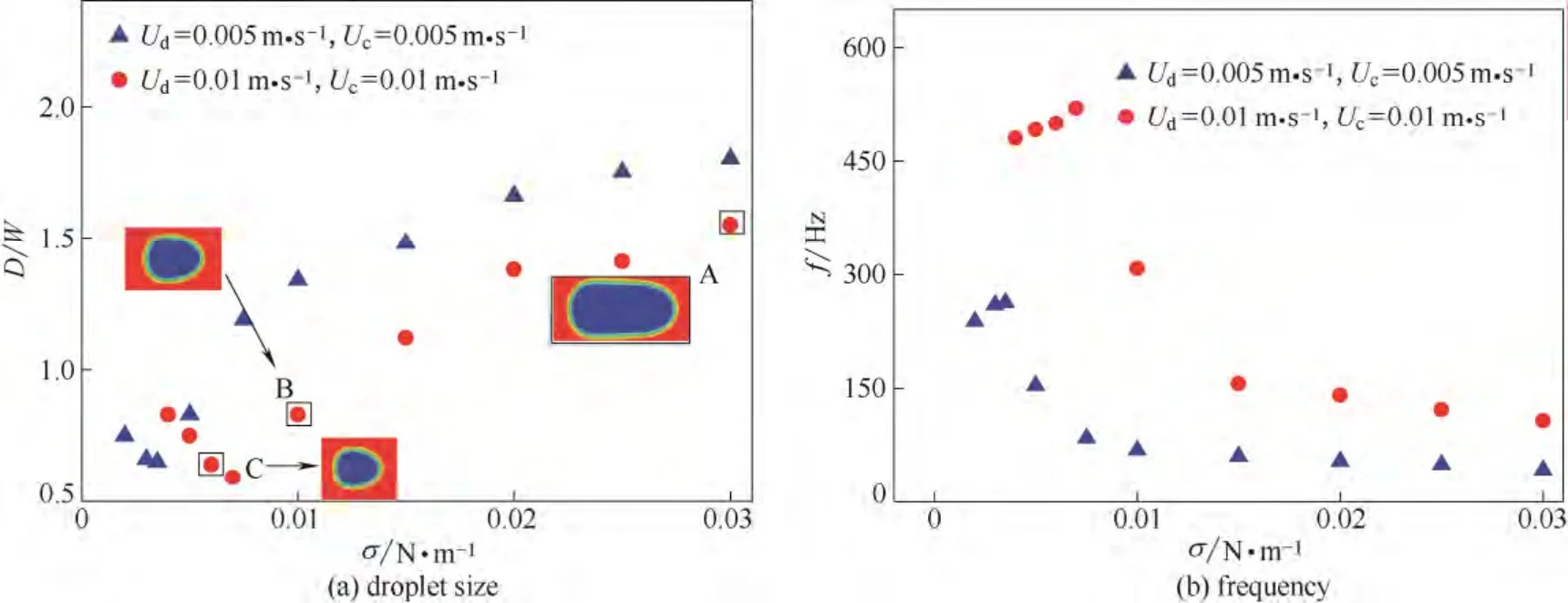
图7 两相表面张力系数对微液滴生成的影响Fig.7 Droplet size and frequency with respect to surface tension

图8 连续相黏度对微液滴生成的影响Fig.8 Droplet size and frequency with respect to viscosity of continuous phase

Gordon 等[28]对于微通道中液滴的形成，提出过表面张力通过建立压降会阻碍液滴的形成。同样，本节也考察了两相表面张力对微液滴生成的尺寸和频率的影响，结果见图7（µd=0.002 Pa·s，µc=0.056 Pa·s）。从图中可看出，表面张力对微液滴生成的影响随着两相流速的变化而不同。在低速条件下（Ud=0.005 m·s-1，Uc=0.005 m·s-1），连续相Ca数较小，这时表面张力对流动的影响起主导作用，随着表面张力系数的减小微液滴的生成机制逐渐由拉伸挤压转换为滴状剪切，微液滴生成的尺寸也逐渐减小，微液滴生成频率则逐渐增大，而且减小和增大的速率随着表面张力系数的减小而增大。对于相同流速比的高速条件下（Ud=0.01 m·s-1，Uc=0.01 m·s-1)，其变化趋势与低速条件下大致相同，但由于在较高流速下，表面张力的影响减小，因此在较小表面张力系数范围内随着表面张力系数的增加，微液滴生成尺寸的增加速率要小于低速条件下的增加速率，但随着表面张力系数的增加，表面张力的影响逐渐增大，液滴的生成尺寸的增加速率迅速增大，而生成频率迅速降低。另外，可以注意到当表面张力系数小于某值时，液滴的生成机制转为射流机制，这时，随着两相表面张力系数的减小，生成液滴的尺寸反而逐渐增大，液柱的长度也逐渐增加，相应的生成频率则逐渐减小。

3.4 连续相黏度对微液滴生成的影响

图8显示了3 种不同液液两相流速条件下微通道内微液滴生成尺寸与频率随连续相黏度的变化（µd=0.002 Pa·s，σ=0.01 N·m-1）。从图中发现生成微液滴的尺寸随着连续相流体黏度的增大而减小，微液滴生成的频率随连续相黏度的增大而增大。在低速条件下（Ud=0.005 m·s-1,Uc=0.005 m·s-1），连续相Ca数较小，表面张力对流动的影响起主导作用。这时增加连续相的黏度，液滴大小和生成频率的变化较小。在高速条件下（Ud=0.01 m·s-1，Uc=0.01 m·s-1），连续相的黏性剪切作用起主导作用。随着连续相黏度的增加，连续相对液滴的剪切作用也增大，因此，液滴生成的大小减小、生成频率升高，且速度越大，液滴大小以及生成频率变化越明显。Fu 等[24-25]对于在十字聚焦微通道中气泡的生成提出过相似的结论，即随着连续相黏度的增加，气泡的尺寸逐渐变小，生成频率逐渐变大。

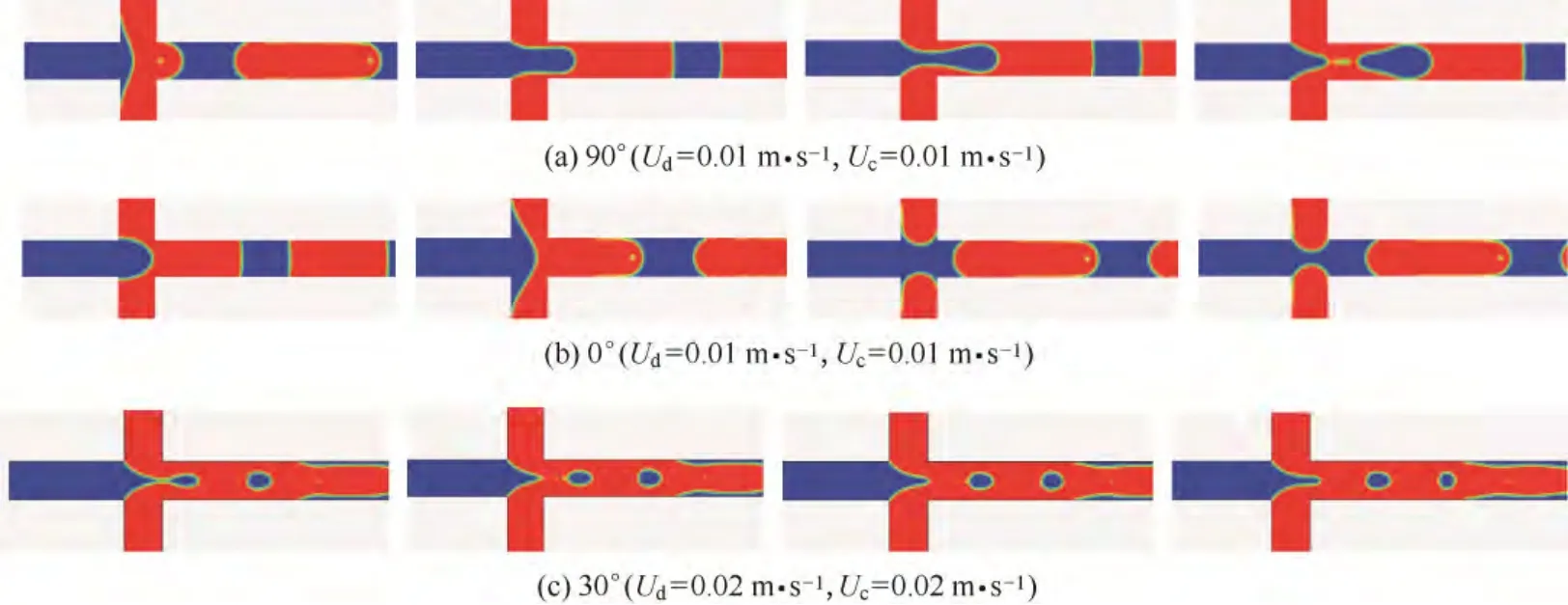
图9 不同接触角下微液滴的生成过程Fig.9 Droplet generation with different contact angles

对于所选的3 组流速工况，连续相黏度的影响 随两相流速的高低而不同：在低速条件下（Ud=0.005 m·s-1，Uc=0.005 m·s-1），连续相Ca数较低，微液滴的生成受连续相黏度影响因素较小。随连续相黏度从0.002 Pa·s 变化到0.056 Pa·s，微液滴的相对尺寸D/W从2.06 减小到1.45，减小了30%，微液滴生成频率从26.0 Hz 增加到58.0 Hz，增加了1.2 倍；在高速条件下（Ud=0.02 m·s-1，Uc=0.01 m·s-1），连续相黏度影响较大。此时微液滴的生成机制随着连续相黏度的增大依次从拉伸挤压模式转换为滴状剪切模式，最后进入射流模式。而且微液滴的相对尺寸从2.51 减小到0.91，减小了64%，微液滴生成频率从93.0 Hz 增加到467.9 Hz，增加了4 倍。

3.5 壁面接触角对微液滴生成的影响

本文最后研究了接触角即壁面润湿性对微液滴生成的影响。图9(a)、(b)显示了壁面接触角分别为90°和0°时微通道内微液滴的生成过程。随着接触角的减小，通道内的界面相对于连续相流体来说从外凸转换为内凹，离散相与壁面的接触面积增大。当流速较小时，液滴的生成机制为拉伸挤压模式，这时无论壁面接触角为180°或是0°，均能生成稳定的单分散液滴；但当两相流速逐渐增大后，微液滴生成进入滴状剪切模式或射流模式，接触角减小会导致两相流动变为环状流，无法稳定生成微液滴，如图9(c)所示。

4 结 论

本文对十字交叉型微通道内的微液滴生成过程利用VOF 模型进行了三维数值模拟，模拟结果与可视化实验吻合良好。随后研究了微液滴生成的不同流型以及两相流量、表面张力、连续相黏度、壁面接触角等参数对液滴生成的影响，具体结论 如下。

（1）液滴量纲1 尺寸D/W随着连续相Ca数的增大而呈现指数衰减趋势。随着两相Ca数（0.001 m·s-1＜Ud＜1 m·s-1，0.001 m·s-1＜Uc＜1 m·s-1）的变化，微通道内W/O 微液滴生成表现为不同的机制：在离散相Ca数较低时（Ud＜0.03 m·s-1），W/O 微液滴的生成模式随着连续相流速的升高，依次经历拉伸挤压模式、滴状剪切模式、单分散射流模式以及紊乱射流模式；当离散相Ca数较高时（Ud＞0.03 m·s-1），则产生滑移流、节状形变流以及管状流等各种环状流模式。其中只有拉伸挤压模式、滴状剪切模式和单分散射流模式能够生成单分散微液滴。

（2）液液两相的流速对微液滴生成的尺寸和频率有较大影响：固定离散相流速下，微液滴的生成尺寸随连续相流速的增大而减小，微液滴的生成频率随连续相的增大而增大。在相同的连续相流速变化范围内，随着离散相流速的增加，微液滴的生成尺寸降低速率以及生成频率的增加速率变快，而且当离散相流速大于0.03 m·s-1时，微液滴的生成全部以射流形式进行。

（3）两相表面张力和连续相黏度对微液滴的影响随连续相Ca数的变化而不同，在低连续相Ca数下，表面张力占主导地位；在高连续相Ca数下，连续相黏度占主导地位。总的来说，生成微液滴的尺寸随表面张力的增大而增大，随连续相黏度的增大而减小。微液滴的生成频率随两相表面张力的增大而减小，随连续相黏度的增大而增大。但对于射流模式下，随表面张力系数的减小，生成微液滴的尺寸反而增加，生成频率降低。

（4）壁面接触角对微液滴生成的影响随流型的不同而不同：对于拉伸挤压流型，随着离散相流体壁面接触角的减小，离散相界面相对于连续相流体从外凸变为内凹，这时离散相与壁面接触面积增大，而且仍能稳定生成微液滴。但随着两相流速的增大，液滴的生成进入滴状剪切和射流模式，这时随着壁面接触角减小，微液滴的生成频率降低，生成难度加大。

[1]Margulies M,Egholm M,Altman WE,et al.Genome sequencing in microfabricated high-density picolitre reactors [J].Nature,2005,437 (7057):376-380

[2]Mardis E R.The impact of next-generation sequencing technology on genetics [J].Trends in Genetics,2008,24 (3):133

[3]Ho Cheung S,Sauret A,Fernandez-Nieves A,et al.Corrugated interfaces in multiphase core-annular flow [J].Physics of Fluids,2010,22 (8):082002

[4]Kim C,Chung S,Kim Y E,et al.Generation of core-shell microcapsules with three-dimensional focusing device for efficient formation of cell spheroid [J].Lab Chip,2011,11 (2):246-252

[5]Umbanhowar P B,Prasad V,Weitz D A.Monodisperse emulsion generationviadrop break off in a coflowing stream [J].Langmuir,2000,16 (2):347-351

[6]Anna S L,Bontoux N,Stone H A.Formation of dispersions using “flow focusing” in microchannels [J].Applied Physics Letters,2003,82 (3):364-366

[7]Dreyfus R,Tabeling P,Willaime H.Ordered and disordered patterns in two-phase flows in microchannels [J].Physical Review Letters,2003,90 (14):144505

[8]Garstecki P,Gitlin I,DiLuzio W,et al.Formation of monodisperse bubbles in a microfluidic flow-focusing device [J].Applied Physics Letters,2004,85 (13):2649-2651

[9]Takeuchi S,Garstecki P,Weibel D B,et al.An axisymmetric flow-focusing microfluidic device [J].Advanced Materials,2005,17 (8):1067-1072

[10]Yobas L,Martens S,Ong W-L,et al.High-performance flow-focusing geometry for spontaneous generation of monodispersed droplets [J].Lab Chip,2006,6 (8):1073-1079

[11]Ong W L,Hua J,Zhang B,et al.Experimental and computational analysis of droplet formation in a high-performance flow-focusing geometry [J].Sensors and Actuators A:Physical,2007,138 (1):203-212

[12]Wang W H,Zhang Z L,Xie Y N,et al.Flow-focusing generation of monodisperse water droplets wrapped by ionic liquid on microfluidic chips:from plug to sphere [J].Langmuir,2007,23 (23):11924-11931

[13]Li W,Young E W K,Seo M,et al.Simultaneous generation of droplets with different dimensions in parallel integrated microfluidic droplet generators[J].Soft Matter,2008,4 (2):258-262

[14]Nisisako T,Torii T.Microfluidic large-scale integration on a chip for mass production of monodisperse droplets and particles [J].Lab Chip,2008,8 (2):287-293

[15]Funfschilling D,Debas H,Li H Z,et al.Flow-field dynamics during droplet formation by dripping in hydrodynamic-focusing microfluidics [J].Physical Review E,2009,80 (1):015301

[16]Zhou Chunfeng,Yue Pengtao,Feng J J.Formation of simple and compound drops in microfluidic devices [J].Physics of Fluids,2006,18 (9):092105

[17]Cubaud T,Mason T G.Capillary threads and viscous droplets in square microchannels [J].Physics of Fluids,2008,20 (5):053302

[18]Liu Haihu,Zhang Yonghao.Droplet formation in microfluidic cross-junctions [J].Physics of Fluids,2011,23 (8):082101

[19]Chen Bin,Guo Fang,Li Guojie,Wang Peng.Three-dimensional simulation of bubble formation through a microchannel T-junction [J].Chemical Engineering Technology,2013,36 (12):1-15

[20]Sur A,Lixin Y,Dong L,et al.Experimental and numerical investigation of two-phase patterns in a cross-junction microfluidic chip//8th International Conference on Nanochannels,Microchannels and Minichannels [C].Montreal,Candan,2010

[21]Kim L S,Jeong H K,Ha M Y,et al.Numerical simulation of droplet formation in a micro-channel using the lattice Boltzmann method [J].Journal of Mechanical Science and Technology,2008,22 (4):770-779

[22]Wang Peng (王澎),Chen Bin (陈斌).Numerical simulation of micro-droplet breakup in T-shaped micro-fluidic chip[J].CIESC Journal(化工学报),2012,63 (4):999-1003

[23]Ling Zhiyong (凌智勇),Zhuang Zhiwen (庄志文),Ding Jianning (丁建宁),et al.Numerical simulation and characteristics study of pressure-driven flow in microtubes [J].Machinery Design and Manufacture(机械设计与制造),2007 (10):37-39

[24]Lu Yutao,Fu Taotao,et al.Scaling of the bubble formation in a flow-focusing device:role of the liquid viscosity [J].Chemical Engineering Science,2014,105:213-219

[25]Fu Taotao,Denis Funfschilling,et al.Scaling the formation of slug bubbles in microfluidic flow-focusing devices [J].Microfluid Nanofluid,2010,8 (4):467-475

[26]Wei Lijuan (魏丽娟),Zhu Chunying (朱春英),et al.Experimental measurement and correlation of droplet size in T-junction microchannels [J].CIESC Journal(化工学报),2013,64 (2):517-523

[27]Xu J H,Li S W,et al.Correlations of droplet formation in T-junction microfluidic devices:from squeezing to dripping [J].Microfluid Nanofluid,2008 (5):711-717

[28]Gordon F Christopher,N Nadia Noharuddin,et al.Experimental observations of the squeezing-to-dripping transitionin T-shaped microfluidic junctions [J].Physical Review E,2008,78 (3):036317