整流罩声振试验蜂窝夹层板建模方法

韩敬永，于开平，宋海洋，杨雨超

（1.哈尔滨工业大学　航天学院，哈尔滨150001；2.中国燃气涡轮研究院，成都610000）

整流罩声振试验蜂窝夹层板建模方法

韩敬永1，于开平1，宋海洋1，杨雨超2

（1.哈尔滨工业大学航天学院，哈尔滨150001；2.中国燃气涡轮研究院，成都610000）

针对整流罩主体结构由蜂窝板结构构成的特点，在使用统计能量分析法进行整流罩结构高频振动噪声环境预示研究时，重点对蜂窝夹层板建模的三明治夹芯板理论、等效板理论和蜂窝板理论三种等效方法进行比较分析。采用蜂窝夹层板的三种不同等效理论对整流罩整尺度结构进行统计能量分析建模，并将预示结果与在混响室内进行的该整流罩声振实验结果进行对比，分析表明三明治夹芯板理论更适用于研究蜂窝板的高频振动特性。

声学；整流罩；蜂窝夹层板；三明治夹芯板理论；噪声振动预示

整流罩结构用于保护航天器有效载荷，在发射起飞阶段要经受非常严酷的力学环境。激励源主要来源于两个方面：一是通过火箭星箭对接面向上传递的机械振动，二是火箭起飞时由大推力发动机系统工作产生的喷气噪声和飞行器高速飞行时产生的气动噪声［1］。其中噪声激励的频率范围可达20 Hz～10 KHz，机械振动的频率成分包含0～2000 Hz，这些宽频激励会导致航天器高结构系数板壳结构产生很高的均方响应加速度，大大降低系统的可靠性。准确的整流罩结构振动噪声预示是制定地面试验载荷条件，确定有效载荷工作环境的关键。王建伟等［2］对整流罩内振动噪声的主动和被动控制技术进行梳理和分析，张国军等［3］采用统计能量法对X-43 A进行理论和试验研究，验证了统计能量对声振环境预示的可靠性。孙目［4］、傅学军［5］等采用统计能量分析方法对某型整流罩噪声环境进行预示，研究了整流罩的降噪结构设计。针对整流罩中的蜂窝夹层板结构，很多学者进行了等效模型的研究。张铁亮［6］对比了不同等效模型在位移、应力、频率精度的差别，Clarkson［7］研究了集中质量、镶嵌块等对蜂窝夹层板模态密度的影响，Renji［8］对复合材料面板蜂窝夹层板的损耗因子进行了试验研究。本文基于统计能量分析原理，对整流罩蜂窝夹层板结构采用三明治夹芯板理论、等效板理论和蜂窝板理论进行等效，建立整流罩统计能量模型，将不同模型的振动噪声预示结果与试验值进行对比分析。

1　整流罩结构简介

某整流罩结构主要由头锥、前锥、柱段、倒锥段、上下星支架和上下星过渡支架组成。其中前锥、柱段均为铝蜂窝夹层板，芯子高度28 mm，边长为5 mm正六边形，铝箔厚度0.05 mm，上下蒙皮为0.4 mm厚铝板。上星过渡支架为芯子高度9 mm的铝蜂窝夹层板。上、下星支架和下星过渡支架为蜂窝夹层板，上下蒙皮为碳纤维布。倒锥段为通过螺栓连接的六块加筋板。由此可以看到，整流罩整体结构主要由铝蜂窝夹层板构成，结构的振动噪声环境也就主要由铝蜂窝夹层板的建模决定，因此本文主要讨论铝蜂窝夹层板的统计能量分析建模问题。

图1　整流罩结构示意图

2　蜂窝夹层板等效模型

蜂窝夹层板的蜂窝部分结构复杂，很难直接对其进行建模，有些情况也不必要直接建模。因此，在蜂窝夹层振动噪声特性问题的研究上，学者们把主要注意力放在蜂窝夹层板等效处理上。目前主要的等效方法有三明治夹芯板理论、等效板理论和蜂窝板理论，分别介绍如下。

2.1三明治夹芯板理论

三明治夹芯板理论只对蜂窝芯子进行等效，将其等效为正交各向异性的均匀连续结构。对于正六边形蜂窝芯子，芯子材料弹性模量、剪切模量、泊松比、密度分别为Es、Gs、μs、ρs。假设蜂窝芯子壁厚t，芯子边长l。蜂窝芯子的等效弹性常数和密度为［9］。

式中γ为修正系数，取决于工艺，一般取0.4～0.6，理论值取1。

2.2等效板理论

等效板理论也称刚度等效理论，将整体蜂窝板等效为与原夹层板不等厚的各向同性板，易于实现，但不能反映芯子形状对夹层板整体性能的影响。满足Kirchhoff假设，等效板的弯曲刚度和拉压刚度为

基于Hoff理论的等刚度法，假设面板为普通薄板，考虑面板的弯曲刚度，由于夹芯很软，忽略夹芯的面内应力，假定z方向的应力应变为零。基于Hoff理论的弯曲刚度和拉压刚度为

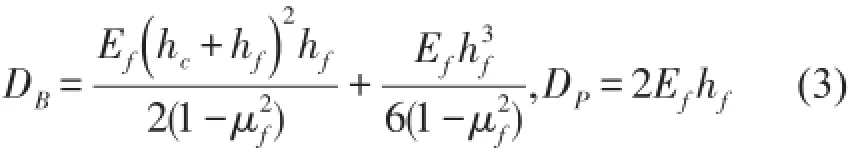
由刚度等效可得等效参数为

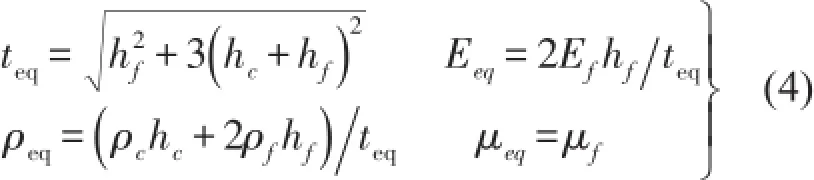
2.3蜂窝板理论

蜂窝板理论，是以动力学方程为基础，基于哈密顿变分原理，将整个蜂窝夹层板等效成等刚度、同尺寸的正交各向异性板，同时考虑了表层和夹层的面内和面外力学特性，推导出等效力学模型的等效力学参数。对于芯子高度2 h，面板厚度d的蜂窝夹层板，其等效参数为［10］

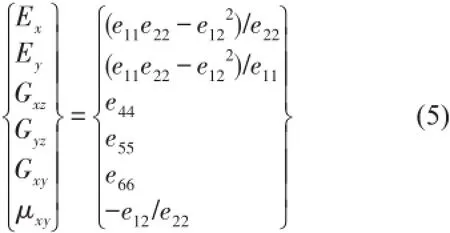
式中

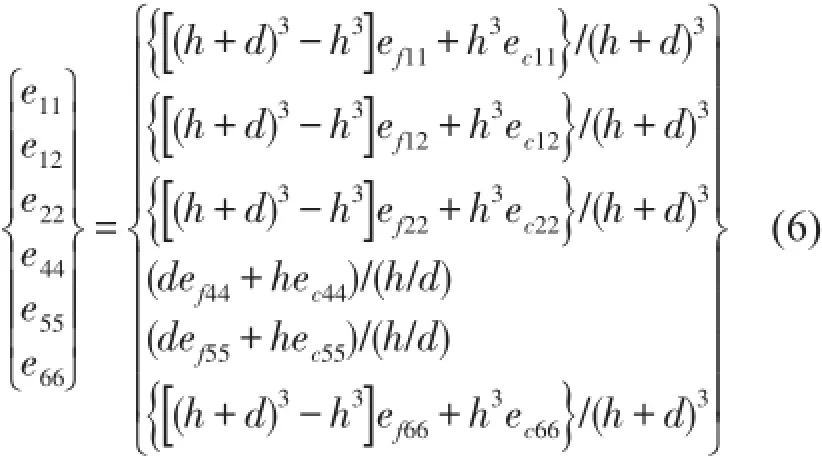
等效密度：ρ=（dρf+hρc）/（h+d）

面板和夹芯的刚度系数efij、ecij表示为

其中Ef、Gf、μf为面板材料参数；k为面板横向剪切影响系数，取值0～1。夹芯的材料参数由夹层板理论求得。

3　整流罩振动噪声预示

根据整流罩结构的有限元模型，按照统计能量子系统的划分准则，建立如图2所示整流罩统计能量模型。模型中共有68个子系统，其中58个结构板壳子系统，3个声腔子系统和7个半无限流场。采用扩散声场模拟混响场激励。

统计能量分析方法的主要参数有模态密度、内损耗因子、耦合损耗因子和输入功率。子系统的模态密度和耦合损耗因子可以由理论计算得到，外载荷采用混响室中测量值。外载荷激励谱值如下表1所示。

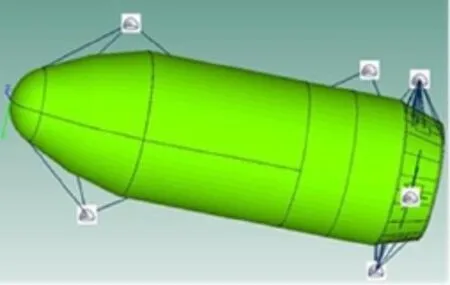
图2　整流罩结构子系统

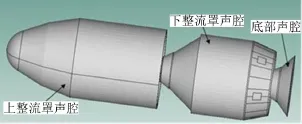
图3　整流罩声腔子系统

各子系统内损耗因子的选取是统计能量分析的关键。由于内损耗因子的机理复杂，使用理论计算存在困难。在缺乏试验数据的情况下，可以通过计算结构响应对内损耗因子的灵敏度，在损耗因子取值区间选取相对合理的值。当然，最准确的方法还是通过试验获取。本文采用文献［4］对典型部件内损耗因子试验测量值拟合出的公式。铝蜂窝夹层板内损耗因子η为

表1　外载荷激励谱值（倍频程）

表2　不同模型上声腔声压级对比/dB

对于蜂窝夹层板的吸声系数，文献［4］给出的拟合公式为α=0.9 f-0.35，在低、中频段与试验值吻合较差。本文中吸声系数在低频取0.05，高频取0.01。

针对整流罩的铝蜂窝夹层板，分别采用上述三种等效方法进行建模，预示整流罩内声场的声压级和部件的振动响应，并与试验结果进行对比。试验中整流罩内声场声压级不均匀，而统计能量模型的预示结果为子系统的平均响应，因此以统计平均量进行对比。各模型中上声腔的声压级对比如下表2所示。

对于结构振动响应，由于振动传感器测量的是各测点X、Y、Z方向的加速度振动响应，而统计能量模型给出的是子系统弯曲模态群、面内剪切和拉伸模态群的响应，文中对比中心频率31.5 Hz～2 000Hz频率范围内三个方向加速度均方值矢量和。各模型中各子系统结构振动响应的对比如下表所示。

表3　不同模型子系统结构振动响应对比/g

表2中声腔声压级的对比结果表明：三种等效理论在31.5 Hz的误差都比较大，主要是因为各子系统在低频段的模态数偏少导致的。在其它频带，除8 000 Hz外，三明治夹芯板理论的预示结果与试验误差均在±3 dB内。等效板理论和蜂窝板理论在4 000 Hz和8 000 Hz的预示结果与试验误差较大。

当波长与夹芯厚度相当时，三明治夹芯板的弯曲应变能主要集中在表层面板关于其自身中性层的弯曲振动，此时其损耗因子或吸声系数可能会与拟合公式有较大差别，从而导致声腔声压级误差较大。柱段子系统的模态密度如下图所示，可见三种等效模型在低频段模态密度相差不大，但在高频段等效板理论和蜂窝板理论与夹芯板理论相差较大。

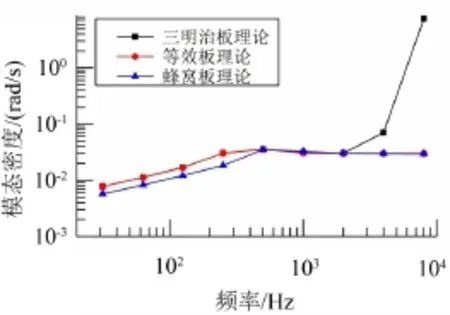
图4　柱段各等效模型模态密度

表3中结构振动响应对比表明：三种等效模型的预示结果相差不大，与试验值误差均在±3 dB之内，并且预示值均大于试验值。主要是因为传感器多位于子系统的边缘部分，用边缘部分的振动响应进行平均导致子系统响应试验值与仿真值相比偏低，此外在31.5 Hz～2000 Hz频带内，各模型中子系统的模态密度相差不大的，因此三种模型的结构振动预示结果相差不大。

4　结　语

针对某整流罩结构的主体结构蜂窝夹层板，采用三明治夹芯板理论、等效板理论和蜂窝板理论三种等效方法，建立预示整流罩结构振动噪声特性的统计能量模型，将三种不同模型的振动噪声预示结果与该整流罩在混响室声振试验环境下的试验结果进行比较分析。结果表明，用三明治夹芯板理论更接近蜂窝板真实振动噪声特性，这与文献［6］的分析结果相同，因此该结论可以推广用于其它型号蜂窝夹层板结构的整流罩统计能量建模。

［1］马兴瑞，于登云，韩增尧，等.星箭力学环境分析与试验技术研究进展［J］.宇航学报，2006，27（03）：323-331.

［2］王建伟，王刚，温激鸿，等.航天器发射阶段声振环境载荷控制技术研究进展［J］.噪声与振动控制，2011，31（1）：1-8.

［3］张国军，闫云聚，李鹏博.基于统计能量法的飞行器结构声振响应分析［J］.噪声与振动控制，2014，34（03）：92-96.

［4］孙目，潘忠文.卫星整流罩噪声环境预示与降噪设计［J］.导弹与航天运载技术，2008，296（4）：6-10.

［5］傅学军，雷勇军.有效载荷整流罩降噪性能的数值分析和优化设计研究［J］.导弹与航天运载技术，2005（6）：12-15.

［6］张铁亮，丁运亮，金海波.蜂窝夹层板结构等效模型比较分析［J］.应用力学学报，2011（03）：275-282.

［7］Clarkson B L，Ranky M F.Modal density of honeycomb plates［J］.Journal of Sound and Vibration，1983，91（1）: 103-118.

［8］Renji K，Shankar Narayan S.Loss factors of composite honeycomb sandwich panels［J］.Journal of Sound and Vibration，2002，250（4）:745-761.

［9］赵金森.铝蜂窝夹层板的力学性能等效模型研究［D］.南京：南京航空航天大学，2006.

［10］徐胜今，孔宪仁，王本利，等.正交异性蜂窝夹层板动、静力学问题的等效分析方法［J］.复合材料学报，2000（03）：92-95.

Study on the Modeling Methods of Honeycomb Sandwich Panels Based on Fairing Vibroacoustic Experiments

HAN Jing-yong1，YU Kai-ping1，SONG Hai-yang1，YANG Yu-chao2
（1.School ofAstronautics，Harbin Institute of Technology，Harbin 150001，China；2.China Gas Turbine Establishment，Chengdu 610000，China）

Three modeling methods of honeycomb panels were studied.The sandwich theory，equivalent plate theory and honeycomb plate theory were compared one another using statistical energy analysis for prediction of high-frequency noise and vibration environment of faring structures.The statistical energy analysis models based on the three equivalent theories were established for the whole-scale fairing structure.The prediction results were compared with the experimental data tested in a reverberation chamber.This study indicates that the sandwich theory is more suitable for studying the highfrequency vibration characteristics of the honeycomb panels than the others.

acoustics；fairing；honeycomb sandwich panel；sandwich theory；noise and vibration prediction

TB533+.3

ADOI编码：10.3969/j.issn.1006-1335.2015.05.013

1006-1355（2015）05-0065-04

2014－10－16

国家自然科学基金项目（11372084）

韩敬永（1987－），男，河北衡水人，博士生，主要研究方向：飞行器声振环境预示研究。

于开平，男，博士生导师。

E-mail:yukp@hit.edu.cn