基于粒子群优化算法的Jiles-Atherton磁滞模型参数计算*1

郝晓亮， 叶美盈

(浙江师范大学 数理与信息工程学院，浙江 金华 321004)

基于粒子群优化算法的Jiles-Atherton磁滞模型参数计算*1

郝晓亮， 叶美盈

(浙江师范大学 数理与信息工程学院，浙江 金华 321004)

粒子群优化算法是一种模拟鸟群捕食行为的群体智能算法，该算法具有简洁、易于实现、没有太多调整参数及不需要梯度信息等特点，且在大多数情况下可快速收敛于最优解．为了描述材料的磁滞特性，提出了一种粒子群优化算法结合MATLAB/Simulink动态仿真集成环境的Jiles-Atherton磁滞回线模型参数计算方法，并分别以无噪及加噪的仿真数据对2组参数值不同的Jiles-Atherton磁滞回线模型进行了数值实验．结果表明，将粒子群优化算法及MATLAB/Simulink动态仿真集成环境应用于Jiles-Atherton磁滞模型的参数计算是有效的．

磁滞回线；粒子群优化算法；磁滞模型；参数计算

0 引 言

磁滞现象是物理系统和电磁设备中常见的一种非线性特性，它对设备是否能稳定运行和系统的安全运转起着重要的作用．例如硅钢片的磁滞特性对变压器偏磁饱和时的运行性能有很大的影响．因此，了解和分析磁滞特性具有重要意义．

根据实验数据建立磁滞模型，并以此进行数值模拟是研究磁滞特性的重要内容之一．目前,研究者已提出了多种描述磁滞现象的模型，常见的有：Bouc-Wen磁滞模型[1-3]、Preisach磁滞模型[4]、Jiles-Atherton(JA)磁滞模型[5]．其中，Bouc-Wen磁滞模型的缺点是各参数之间的关系不直观，物理意义不明确，且表达式以导数或微分形式出现，增大了系统的维数，使分析的难度加大[6]．Preisach磁滞模型则是一种偏数学意义的模型，Preisach权重函数的确定及相关参数的实验测量难度较大，以致求解困难[7-9]，且数学表达式也太过复杂．Preisach磁滞模型的另一缺陷是:若考虑各向异性、频率诸因素，Preisach模型将变得极为复杂，从而给数值计算和计算机编程等带来诸多麻烦．JA磁滞模型是依据物理机理推导而得的一种模型，该模型具有清晰的物理意义，能够真实地描述磁场强度H与磁感应强度B之间(即B-H)的非线性关系，通过求解JA磁滞模型方程能得到准确的B-H磁滞回线，且参数也相对较少，特别适用电磁器件的分析[10-11]．因此，JA磁滞模型是目前最为常用的一种磁滞模型[5]．

值得注意的是，在建立JA磁滞模型的过程中，虽然模型参数的近似值只需要借助饱和磁滞回线的测量数据即可获得，但因磁滞非线性的复杂性，如何精确计算这些参数一直是个不易解决的关键问题．在过去几十年里，许多传统的非线性优化方法已被用于解决JA模型参数计算问题,然而这些优化方法易受初始值选择的影响，寻优过程易陷入局部极小．为了克服这一缺点，近年来迅速发展的智能优化算法吸引了人们的注意，例如，遗传算法(Genetic Algorithm，GA)因其良好的全局收敛特性，易于得到比传统优化方法更好的参数计算结果．文献[12-19]已成功地将遗传算法应用于JA模型的参数计算，但GA算法的“早熟”现象及接近最优点收敛较慢的问题限制了其进一步推广应用[3]．

粒子群优化(Particle Swarm Optimization，PSO)算法是基于观察动物的社会行为，例如模拟鸟类、鱼群、蚁群捕食行为的智能优化算法，该算法最早由美国电气工程师Eberhart和社会心理学家Kennedy于1995年提出[20]．相比于GA算法，PSO算法有一些更吸引人的特性[21]，其主要特点是具有记忆，因而好的解决方案信息易被保留至下一代.而在GA算法中，先前的信息会随着种群的改变而破坏．此外，PSO算法得益于粒子间的合作，种群中的粒子之间可相互共享信息．目前，PSO算法在众多邻域都引起了很大的关注，已在医疗诊断[22]、神经网络训练[23]、太阳能电池参数提取[24]、电气设备的功率反馈和电压控制[25]、机器人路径规划[26]等方面获得了广泛应用．为了得到更有效的JA磁滞模型建模方法，本文尝试在MATLAB/Simulink动态仿真集成环境中，将PSO算法应用于JA磁滞模型的参数计算,通过Simulink动态仿真JA模型，并应用PSO算法最小化磁感应强度的实验值和计算值之间的差别,指导JA模型的参数向真值逼近．

1 JA模型

JA模型考虑了实际材料受杂质、非磁性包含物、不均匀压力及颗粒、孔洞等因素的影响，将磁化强度分解为不可逆磁化分量和可逆磁化分量2部分．其中:不可逆磁化分量缘于畴壁取代，即钉扎的阻碍作用；而可逆磁化分量则缘于畴壁弯曲，从而得到了关于磁滞现象的一个简单微分表达式．JA模型参数较少,仅有一个一阶微分方程,计算量低，并且包含了磁滞现象的主要特征：初始磁化曲线、饱和磁化曲线、矫顽力、剩磁和磁滞损耗等．

设JA模型的不可逆磁化分量为Mirr，可逆磁化分量为Mrev，则总磁化强度为

M=Mirr+Mrev. (1)

式(1)中的不可逆磁化分量Mirr满足微分方程

式(2)中：H为磁场强度；Man为非磁滞磁化强度；α为平均场参数；k为钉扎阻碍作用引起的磁滞损失参数；μ0为真空磁导率；δ为方向系数．式(2)中的δ与dH/dt有关，当dH/dt>0时(H向正方向增加)，δ=1，而当dH/dt<0时(H向负方向增加)，δ=-1．式(2)中的Man可表示为

式(3)中：a为形状参数；Ms为饱和磁化强度；He为有效磁场强度且满足

由于非磁滞磁化位移而导致2个钉扎之间畴壁的膨胀，式(1)中的可逆磁化分量Mrev可表示为

Mrev=c(Man-M). (5)

式(5)中，c为磁畴壁弯曲常数.对式(5)求微分，可得

由式(1)、式(2)、式(6)可得到JA模型磁化强度的微分表达式

式(7)中共涉及5个参数：c,k,α,a,Ms．这些参数共同决定了初始磁化曲线及磁滞回线的形状特性．

为了得到B-H磁滞回线，需算得磁感应强度B．若已知磁场强度H及磁化强度M，则磁感应强度B为

B=μ0(H+M). (8)

根据实验数据计算式(7)中的5个参数，本质上是求解优化问题．本文采用粒子群优化算法计算这些参数．计算时，衡量优化性能优劣的目标函数定义为

式(9)中：SV为磁感应强度B的实验值；OV为磁感应强度B的计算值；N为实验数据的个数．计算时通过最小化磁感应强度B的实验值和计算值之间的差别,指导JA模型的5个参数向真值逼近．在本文的数值实验中，将以仿真值替代实验值．

2 PSO算法基本原理

基本PSO算法初始化时，首先随机产生一群粒子(随机解)，迭代过程中每个粒子在搜索空间中“飞翔”．在每个具体的时刻，每个粒子都有一个位置矢量和速度矢量，其维数代表了问题解空间的维数．若第i个粒子的位置和速度分别记为Xi，Vi，并假设问题的搜索空间是一个d维空间，则粒子的位置和速度可以表示为：Xi=[xi1,xi2,…,xid]，Vi=[vi1,vi2,…,vid]．

在迭代过程中，粒子通过跟踪2个“极值”不断调整自己的位置，进行更新．第一个就是粒子本身所找到的最优解，这个解被称为“个体极值”或个体最优解，第i个粒子的个体最优解记为Pi=[pi1,pi2,…,pid]；另一个极值是整个种群目前所找到的最优解，称为“全局极值”或“全局最优解”，记为Pg=[pg1,pg2,…,pgd]．粒子根据式(10)来更新自己的速度和位置：

(10)

式(10)中：t为当前迭代次数；c1,c2为常数，称为加速因子；r1,r2为[0,1]的随机数；w称为惯性因子．第j维的位置和速度变化范围分别为[-xj,max,xj,max]和[-vj,max,vj,max]，迭代中若某一维的xi,j或vi,j超过边界则可取边界值．

3 JA磁滞模型的参数计算

为了计算JA模型的参数，本文建立了基于MATLAB/Simulink的JA模型参数计算仿真平台．在该平台中，JA磁滞模型参数与B-H磁滞回线之间的关系由Simulink动态仿真集成环境构成的仿真模型确定，即在PSO方法优化程序运行过程中，只要提供磁滞模型的5个参数(c,k,α,a,Ms)，就可以由Simulink仿真模型精确算得B-H磁滞回线数据．考虑式(7)是对磁场强度H求微分的表达式，因此,对其两边同乘dH/dt，得

由此可将式(7)转化为对时间的微分．所以根据式(11),JA模型可由Simulink进行与时间相关的动态仿真．在Simulink动态仿真JA模型时，采用计算精度较高的4阶龙格-库塔(Runge-Kutta)法求解，时间步长为0.005 s，激励信号频率为5 rad/s．

在利用本文提出的PSO方法计算JA模型参数时，种群中的每一个粒子被视为JA模型参数的一个潜在解，因此,第i个粒子的位置可表示为xi(ci,ki,αi,ai,MSi)，即每个粒子的位置和速度的维数都是5维的．在计算过程中，以目标函数式(9)作为PSO方法的适应度函数，通过PSO方法自动调节5个参数的值，使磁感应强度B的实验值(或仿真值)与计算值的偏差最小，从而实现对JA模型参数的计算，得到磁滞回线．

以下是应用PSO及MATLAB/Simulink计算JA模型参数的步骤：

1)设定PSO算法的控制变量，包括种群规模、惯性因子、最大迭代次数、模型参数的维数及搜索空间等;

2)随机产生模型参数的初始值，即初始化群体中各粒子的位置和速度；

3)调用Simulink形式的JA模型，按式(9)计算粒子的适应度，若得到更优的pij和pgj，则更新并保存当前的最优值；

4)依照式(10)更新每个粒子的速度和位置；

5)若未能达到预先设定的最大迭代次数，则返回3)；否则停止运算，并输出最优的适应度值(即目标函数值)及对应的优化模型参数值.

4 数值实验结果与讨论

本文数据实验中所用的JA模型参数真值分别来源于文献[27]与[28]．其中，文献[27]给出的是一组低碳钢SAE1010环形材料(内径60 mm，外径79.04 mm，高度9.52 mm)的JA模型参数集(以下称参数集1)；而由文献[28]给出的则是一组碳化铁(Fe3C)材料对应的JA模型参数集(以下称参数集2)．在本文的JA模型参数计算数值实验中，参数集1的采样点数为261个，磁场强度H的最大值为2 600 A/m；参数集2的采样点数为361个，磁场强度H的最大值为6 100 A/m．本文分别在仿真数据无噪和加噪2种情况下，验证了PSO方法计算JA磁滞回线模型参数的可行性．

对于PSO的控制变量，本文取种群规模PS=50，最大迭代次数tmax=500，5个模型参数的搜索空间均设定为其真值附近±100%以内的区域．仿真数据无噪时，对于参数集1，取w=1，c1=c2=2；而参数集2，则取w=0.6，c1=c2=1.7．仿真数据加噪时，w在迭代过程中均由0.9到0.4呈线性下降，并取c1=c2=2．

4.1仿真数据无噪时的参数计算

此时，通过直接将参数集1或参数集2加入Simulink的JA模型，并求解该模型即可得到无噪的仿真数据序列．

在用无噪仿真数据计算JA模型参数时，理论上目标函数最小值应该为0，即式(9)中磁感应强度B的仿真值与计算值应相等．这种情况下可认为计算所得的最优JA模型参数与产生仿真数据所用的参数集1或参数集2相同(实际因数值计算误差会略有不同)．因此，可以通过无噪仿真数据的数值实验观测PSO方法的计算精度．

图1(a)与(b)分别是以参数集1、2利用无噪仿真数据时PSO方法JA模型参数计算所得的磁滞特性．比较图1中的磁滞回线与原始无噪仿真数据，可见无论是参数集1还是参数集2，对于无噪仿真数据，两者均能很好地吻合．图2(a)与(b)则分别展现了PSO方法在参数集1、2的JA模型参数计算过程中，目标函数值F随迭代次数t的变化情况，可见PSO方法能快速收敛．相关的JA模型参数真值与PSO计算值的比较列于表1，显然模型参数的计算值与真值几乎一致．特别地，表1所列参数集1对应的计算值与真值完全相同(实际上若数据位数取足够多，两者仍会略有差异)．

图1 无噪仿真数据时PSO方法JA模型参数计算的磁滞特性

应用无噪仿真数据以4种PSO程序运行模式计算JA模型参数的结果列于表2．其中程序运行的时间tp与软硬件环境有关，本文数值实验所用的计算机配置：CPU为INTEL双核酷睿2，内存为2 GB，操作系统为Windows 7/64位，MATLAB为R2010a版本．由表2可知：对于无噪仿真数据，不同情况的参数计算耗时tp相差并不大，均不需花太多的时间，且计算结束时，目标函数值F除参数集2在PSO程序Model=0和3时略差些(说明正确选择PSO算法的控制参数是有必要的)，其余情况均很小．总之，应用PSO方法在大多数情况下都可得到误差较小的计算结果．

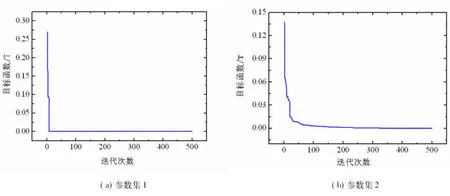
图2 无噪仿真数据时PSO方法目标函数值随迭代次数的变化

表1 JA模型参数真值与无噪仿真数据时PSO计算值的比较

表2 无噪仿真数据时PSO在不同模式下对JA模型参数集1、2计算结果的比较

4.2仿真数据加噪时的参数计算

考虑到在测量B-H磁滞数据的物理实验时不可避免地会受到来自测量仪器本身的误差及外部环境干扰等因素的影响，以致实际得到的B-H实验数据并不“纯净”，其中必定包含测量噪声．因此，笔者在此增加了仿真数据加噪后的数值实验，以进一步验证PSO方法的有效性．

设在无噪数据序列上所叠加的测量噪声为

式(12)中：r为一组数据个数与无噪数据序列相同的、均值为0、方差与标准差均为1的正态分布随机数;Ne则表示所叠加的噪声水平．在以下数值实验中分别取Ne=0.015及0.030，以检验不同测量噪声水平的影响．

仿真数据加噪后应用PSO方法计算JA模型参数获得的磁滞特性见图3．由图3(a)～(d)可看出：参数集1、2的磁滞回线与加噪后的仿真数据吻合程度有所降低，显然噪声水平越高,两者的差异就越大，但即使Ne=0.030,其误差在工程上也仍可接受．可见无论是参数集1还是参数集2，即使对于加噪仿真数据，两者均能很好地吻合.

图4是仿真数据加噪后目标函数值随迭代次数的变化情况，表明此时PSO算法仍能比较快地收敛．表3列出了仿真数据加噪后PSO方法的JA模型参数计算结果．由表3可知，加噪后磁滞模型中的4个参数k,α,a,Ms的计算值与真值仍然接近，但参数c对计算误差比较敏感，计算值与真值偏离较大．比较表1～表3，总体来说仍是噪声水平越高,误差越大，其原因不难理解，仿真数据加噪后目标函数值必然大于0．根据表3可知，加噪后对计算耗时并无影响，与未加噪声前依然相近．

图3 不同加噪水平仿真数据时PSO方法JA模型参数计算的磁滞特性

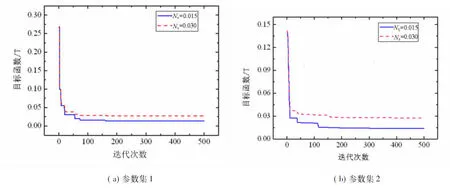
图4 不同加噪水平仿真数据时PSO方法目标函数值随迭代次数的变化

表3 仿真数据加噪后PSO方法的JA模型参数计算结果

5 结 论

本文尝试将PSO算法结合MATLAB/Simulink动态仿真集成环境应用于JA磁滞模型参数计算．数字实验结果表明，当仿真数据未加噪声时，应用本文提出的方法可以得到几乎与模型参数真值一致的计算结果；即使在仿真数据加噪情况下，该方法仍能得到较高的参数计算精度，且由计算所得参数绘制的磁滞回线与仿真数据相吻合，说明该方法有较高的稳定性．因此，本文提出的方法是有效的．

[1]Wen Y K.Method for random vibration of hysteretic systems[J].Journal of the Engineering Mechanics Division,1976,102(2):249-263.

[2]Bouc R.Forced vibration of mechanical systems with hysteresis[C]//Proceedings of the Fourth Conference on non-linear Oscillation.Prague:1967:315.

[3]Ye Meiying,Wang Xiaodong.Parameter estimation of the Bouc-Wen hysteresis model using particle swarm optimization[J].Smart Materials and Structures,2007,16(6):2341.

[4]Mayergoyz I D.Mathematical models of hysteresis[J].IEEE Transactions on Magnetics,1986,22(5):603-608.

[5]Jiles D C,Atherton D L.Theory of ferromagnetic hysteresis[J].Journal of Applied Physics,1984,55(6):2115-2120.

[6]李韶华,杨绍普.滞后非线性模型的研究进展[J].动力学与控制学报,2006,4(1):8-15.

[7]Mayergoyz I D,Adly A A.Numerical implementation of the feedback Preisach model[J].IEEE Transactions on Magnetics,1992,28(5):2605-2607.

[8]Mayergoyz I D,Friedman G.Generalized Preisach model of hysteresis[J].IEEE Transactions on Magnetics,1988,24(1):212-217.

[9]Ge P,Jouaneh M.Generalized preisach model for hysteresis nonlinearity of piezoceramic actuators[J].Precision Engineering,1997,20(2):99-111.

[10]Annakkage U D,McLaren P G,Dirks E,et al.A current transformer model based on the Jiles-Atherton theory of ferromagnetic hysteresis[J].IEEE Transactions on Power Delivery,2000,15(1):57-61.

[11]Leite J V,Sadowski N,Kuo-Peng P,et al.The inverse Jiles-Atherton model parameters identification[J].IEEE Transactions on Magnetics,2003,39(3):1397-1400.

[12]Wilson P R,Ross J N,Brown A D.Optimizing the Jiles-Atherton model of hysteresis by a genetic algorithm[J].IEEE Transactions on Magnetics,2001,37(2):989-993.

[13]Chan Chehang,Liu Guangjun.Hysteresis identification and compensation using a genetic algorithm with adaptive search space[J].Mechatronics,2007,17(7):391-402.

[14]Chwastek K,Szczyglowski J.Identification of a hysteresis model parameters with genetic algorithms[J].Mathematics and Computers in Simulation,2006,71(3):206-211.

[15]Lu Hailiang,Wen Xishan,Lan Lei,et al.A self-adaptive genetic algorithm to estimate JA model parameters considering minor loops[J].Journal of Magnetism and Magnetic Materials,2015,374:502-507.

[16]Leite J V,Avila S L,Batistela N J,et al.Real coded genetic algorithm for Jiles-Atherton model parameters identification[J].IEEE Transactions on Magnetics,2004,40(2):888-891.

[17] Salvini A,Fulginei F R.Genetic algorithms and neural networks generalizing the Jiles-Atherton model of static hysteresis for dynamic loops[J].IEEE Transactions on Magnetics,2002,38(2):873-876.

[18]Cao Shuying,Wang Boweng,Yan Rongge,et al.Optimization of hysteresis parameters for the Jiles-Atherton model using a genetic algorithm[J].IEEE Transactions on Applied Superconductivity,2004,14(2):1157-1160.

[19]Fulginei F R,Salvini A.Softcomputing for the identification of the Jiles-Atherton model parameters[J].IEEE Transactions on Magnetics,2005,41(3):1100-1108.

[20]Kennedy J,Eberhart R.Particle swarm optimization[C]//Purdue school of engineering and technology.Proceedings of the IEEE International Conference on Neural Networks.Perth:IEEE Press,1995:1942-1948.

[21]Slade W H,Ressom H W,Musavi M T,et al.Inversion of ocean color observations using particle swarm optimization[J].IEEE Transactions on Geoscience and Remote Sensing,2004,42(9):1915-1923.

[22]Hsieh Y Z,Su M C,Wang P C.A PSO-based rule extractor for medical diagnosis[J].Journal of Biomedical Informatics,2014,49:53-60.

[23]Kennedy J,Eberhart R C,Shi Y.Swarm Intelligence[M].San Francisco:Morgan Kaufmann,2001.

[24]Ye Meiying,Wang Xiaodong,Xu Yousheng.Parameter extraction of solar cells using particle swarm optimization[J].Journal of Applied Physics,2009,105(9):094502.

[25]Yoshida H,Kawata K,Fukuyama Y,et al.A particle swarm optimization for reactive power and voltage control considering voltage security assessment[J].IEEE Transactions on Power Systems,2000,15(4):1232-1239.

[26]孙波,陈卫东,席裕庚.基于粒子群优化算法的移动机器人全局路径规划[J].控制与决策,2005,20(9):1052-1060.

[27]Hernandez E D M,Muranaka C S,Cardoso J R.Identification of the Jiles-Atherton model parameters using random and deterministic searches[J].Physica B:Condensed Matter,2000,275(1/3):212-215.

[28]Jiles D C,Atherton D L.Theory of ferromagnetic hysteresis[J].Journal of Magnetism and Magnetic Materials,1986,61(1/2):48-60.

(责任编辑 杜利民)

ParametercalculationoftheJiles-Athertonhysteresismodelusingparticleswarmoptimizationalgorithm

HAO Xiaoliang, YE Meiying

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

Particles swarm optimization algorithm was a kind of swarm intelligence algorithm simulating birds feeding behavior. The algorithm had the advantages of concision, easy implement, few control parameters, did not need the gradient information, and fast convergence to optimal solution in most cases．In order to describe the hysteresis characteristics of the material， it was proposed a method of the particle swarm optimization algorithm combination with MATLAB/Simulink dynamic simulation integration environment to calculate the Jiles-Atherton hysteresis loop model parameters. By means of noise-free and noisy simulation data, the numerical experiments of Jiles-Atherton hysteresis loop model with the two groups of different parameter values were carried out. The results indicated that the particle swarm optimization algorithm combination with MATLAB/Simulink dynamic simulation integration environment was an effective technique for the parameters calculation of Jiles-Atherton hysteresis model．

hysteresis loop; particle swarm optimization algorithm; Jiles-Atherton hysteresis model; parameter calculation

10.16218/j.issn.1001-5051.2015.02.003

2015-01-12

国家自然科学基金资助项目(51305407)

郝晓亮(1988-)，男，山西晋中人，硕士研究生．研究方向：理论物理．

叶美盈．E-mail： ymy@zjnu.cn

TM936.3

A

1001-5051(2015)02-0133-09