基于HMM—GJR的中国燃油期货市场VaR风险测度

徐凯++陈粘++傅祺炜

【摘 要】 以中国燃油期货市场为研究对象，首先引入了隐马尔科夫模型（Hidden Markov Models，HMM）对其进行波动状态刻画，进而采用HMM-GJR模型对燃油期货市场波动率进行描述，再对燃油期货市场进行VaR风险测度，并运用Back-testing方法检验了VaR风险测度模型的可靠性。研究结果表明：中国燃油期货市场表现出了明显的高、低两种波动状态，且HMM模型对燃油期货市场的高波动状态刻画具有显著的灵敏性；HMM（2）-GJR模型能够准确刻画燃油期货市场收益波动率；基于HMM（2）-GJR模型的燃油期货市场VaR风险测度更加有效。

【关键词】 中国燃油期货市场； HMM-GJR模型； VaR风险测度

中图分类号：F224 文献标识码：A 文章编号：1004-5937（2015）16-0027-04

一、引言

能源作为最重要的战略物资，对经济发展具有决定性的影响，因而备受各方关注。燃油期货市场作为能源市场的一个重要组成部分，投资者可以利用它来规避能源现货市场价格波动所带来的风险。倘若不能对燃油期货市场进行有效的风险管理，就可能加剧能源市场的风险危机。因此，强化燃油期货市场风险管理，对于维护市场稳定以及促进经济发展具有极其重要的意义。

在燃油期货市场风险管理中，风险测度方法尤为重要。目前常用方法是VaR（Value at Risk），该方法不仅能够直观地表达出金融市场风险值的大小，同时又拥有较好的统计学原理作为支撑，因而受到各大金融机构以及学者的高度关注。因此，本文采用VaR模型对燃油期货市场进行风险测度。

然而，对燃油期货市场进行风险测度的关键是波动模型的选取。长期以来，以Bollerslev为代表的众多学者提出了许多不同类型的GARCH簇模型，由于能够较好地刻画出波动率的时变性、聚集性而具有广泛的适用范围。但是，金融收益波动率除具有聚集性外，还具有杠杆效应，因而仍采用GARCH簇模型就可能无法准确地刻画燃油期货市场波动率。而Glosten et al.（1993）提出的GJR模型不仅能够刻画出金融收益波动率的聚集性等，更为重要的是，GJR模型还能够有效地刻画金融收益波动率的杠杆效应，进而能够更加准确地描述金融收益波动率。因此，本文使用GJR模型对燃油期货市场进行波动率刻画。

特别需要注意的是，燃油期货市场波动率刻画的准确性不仅与波动模型的选取有关，更受其波动状态的制约。燃油期货市场由于受到金融危机等因素影响，其收益波动率可能出现结构突变而表现出多波动状态。而隐马尔科夫模型（Hidden Markov Models，HMM）不仅能够刻画金融收益波动率的多波动状态，更为重要的是，它由一个双内嵌式的随机过程对波动状态进行估计，能够消除主观因素对波动状态刻画的误判，使得对金融市场波动状态的刻画更加准确。因此，本文引入HMM模型对燃油期货市场进行波动状态刻画，以期能够提高对其波动率描述的准确性。

迄今为止，国内外有许多学者对HMM模型进行了详细的分析。Eddy（1996）分析了HMM模型的实现原理，进而使用HMM模型对蛋白质结构状态进行预测；Chong and Reymer（2012）使用HMM-GARCH模型对粒子的运动状态进行刻画，研究表明，HMM模型能够更加准确地刻画出粒子的运动状态。虽然，关于HMM模型的研究都取得了较为显著的成果，但这些成果主要是基于遗传学、生物学以及物理学等方面取得的，在经济学方面的研究还比较缺乏，而本文不仅对中国燃油期货市场波动状态进行了刻画，而且还基于HMM-GJR模型对中国燃油期货市场进行了VaR风险测度。国内已有许多学者对中国能源期货市场进行研究，淳伟德等（2013）对典型事实下的上海燃油期货市场进行VaR风险测度研究，取得了较显著的成果；王鹏和魏宇（2012）基于GARCH簇模型对中国燃油期货市场分别采用VaR与ES风险测度，得出对于风险测度而言，FIGARCH-SKST模型是一个相对合理的选择。虽然，他们的研究都取得了较为显著的成果，但就所掌握的研究文献而言，尚未发现有人引入HMM模型对燃油期货市场波动状态进行研究，少有人使用HMM-GJR模型对燃油期货市场进行波动率刻画，也更少有人采用基于HMM-GJR模型对中国燃油期货市场进行VaR风险测度。由此可见，与已有的研究成果相比，本文具有明显的创新性。

二、研究方法

HMM模型是马尔科夫模型（Markov Model）的进一步发展，它通过一个隐含的状态转移序列（即一个随机的Markov过程）和一个与隐状态相关的观测序列共同对燃油期货市场波动状态进行推断。但是，对于HMM而言，燃油期货市场的波动状态不能直接观测，只能通过随机过程的输出观测序列进行推断。

首先，假设燃油期货市场呈现出三种波动状态S={1，2，3}，其中1、2、3分别表示燃油期货市场处于低、中、高三种波动状态，并对其收益波动率序列{rt}■■构建一阶齐次HMM模型，从而有其收益率所对应的隐状态序列为{st}■■，其中st∈S。又设其状态转移概率矩阵为A=（aij），满足如下条件：

aij=p{st=jst-1=i}

■aij=1，0≤aij≤1，i=1，2，3 （1）

当燃油期货市场收益波动率处于状态j时，所对应的观察值概率分布为B={bj（k）}，其中bj（k）=p{rt=vkst=j}，观察值vk∈（-∞，+∞）。燃油期货市场的初始状态概率分布为π={πiπi=p（st=i）}，i=1，2，3。

可将HMM模型参数简记为λ={A，B，π}，而要对燃油期货市场波动率进行测度，就需要先对其波动状态进行刻画，并且需要解决模型训练、似然函数计算以及隐状态估计这三个基本问题。

（1）模型训练。在给定的模型参数以及用于训练的观测序列O={O1，O2，…，Ot}下，通过Baum-Welch（EM）算法来调整模型参数λ，使得参数能够更准确地拟合观测数据，即存在模型参数λM L=arg ■ f（Oλ）。

（2）似然值计算。在给定模型参数λ下，通过前向-后向算法（Forth-Back）计算观测序列O={O1，O2，…，Ot}的似然值，似然函数f（Oλ）表示模型参数λ拟合观测序列的精确度。

（3）隐状态估计。在给定的模型参数λ和观测序列O={O1，O2，…，Ot}下，基于优化理论，通过Viterbi算法估计最可能的隐状态序列Q={q1，q2，…，qt}。

据此，通过上述三个步骤可得到燃油期货市场的波动状态及其转移概率，进而可使用HMM-GJR模型对其波动率进行描述。

其次，用xt表示t时期燃油期货的收盘价，并定义当期收益率rt为连续复利收益率：

rt=ln（xt /xt-1） （2）

然而，由于受到金融危机、中国能源期货市场自身监管机制等因素的影响，燃油期货市场收益波动率可能呈现出多种波动状态，因而单机制的GJR模型不能对其进行有效刻画。因此，本文构建HMM-GJR（1，1）模型对燃油期货市场进行波动率刻画。

rt=ω■+εt

εtψt-1：N（0，σ■■） （3）

σ■■=ω■+α■ε■■+β■σ■■+γ■ψt-1ε■■

其中，ψt为指示变量，满足如下条件：

Ψt=1，εt<00，εt≥0 （4）

参数αs■、βs■、γs■、ωs■均依赖于t时刻的状态st。设直至t-1时刻条件Ωt-1下收益率rt处于st状态的先验概率为p（stΩt-1），则有■p（stΩt-1）=1。

J.P.Morgan提出了风险测度方法，满足如下模型：

VaR■■=ωt+zασt （5）

其中，ωt表示资产在第t时刻收益率均值；α是置信水平；VaR■■是第t时刻α置信水平下的风险值；zα表示金融收益分布在α水平下的分位数；σt表示第t时刻条件波动率。

三、VaR风险测度模型的评价方法

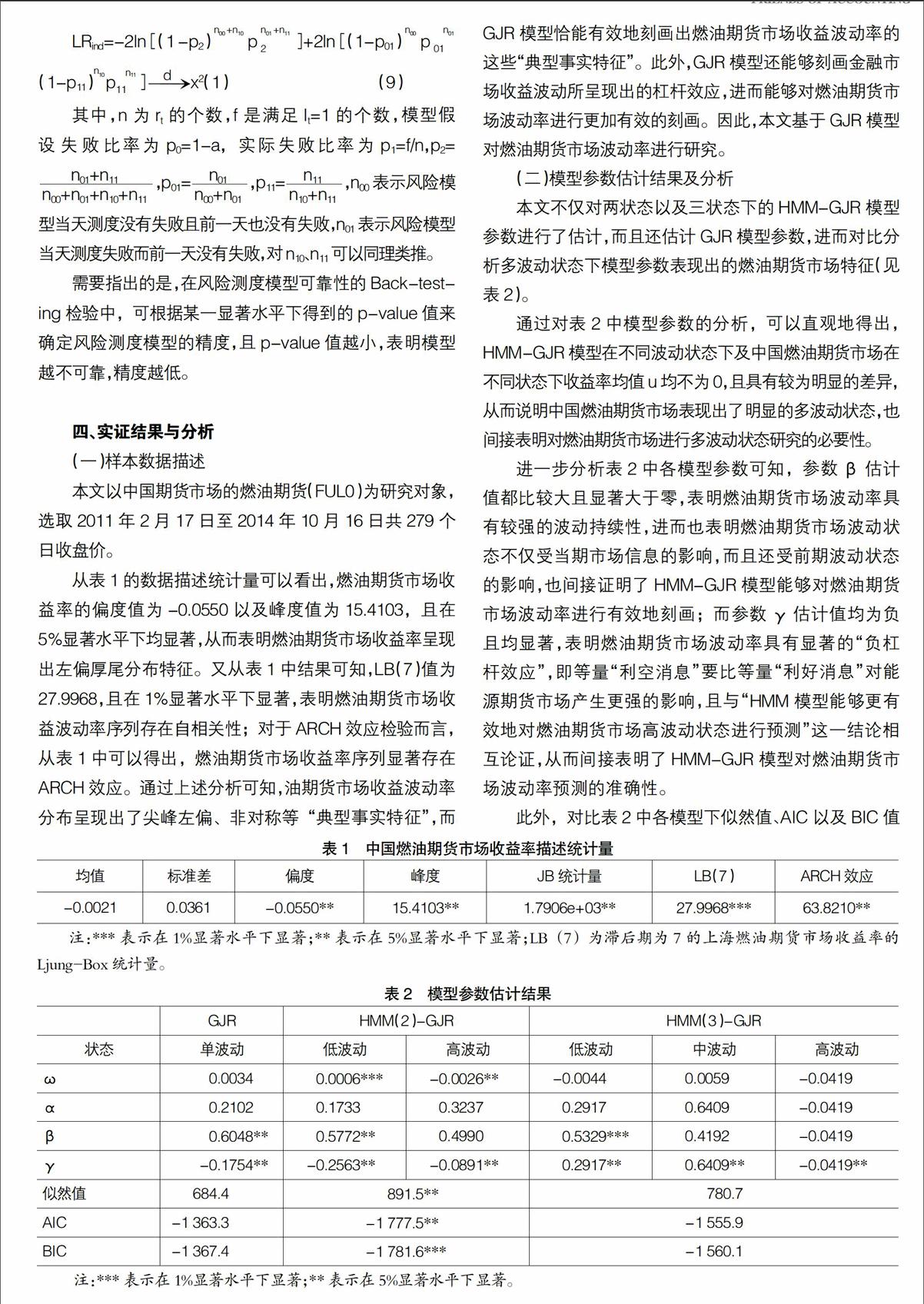
要对金融市场进行有效的风险管理，关键是风险测度模型的可靠性。本文采用Back-testing方法对燃油期货市场的VaR风险测度进行检验。设rt

It=1 rt≥VaR■■0 rt

Christoffersen构建了一个依概率分布服从自由度为2的卡方分布条件统计量LRcc。该统计量不仅考虑了模型测度失败比率与假设比率是否一致的统计量LRu c，而且还考察了失败情况是否为随机情况的统计量LRind，从而使得模型检验具有更强的参考价值。统计量LRcc表达式为：

需要指出的是，在风险测度模型可靠性的Back-testing检验中，可根据某一显著水平下得到的p-value值来确定风险测度模型的精度，且p-value值越小，表明模型越不可靠，精度越低。

四、实证结果与分析

（一）样本数据描述

本文以中国期货市场的燃油期货（FUL0）为研究对象，选取2011年2月17日至2014年10月16日共279个日收盘价。

从表1的数据描述统计量可以看出，燃油期货市场收益率的偏度值为-0.0550以及峰度值为15.4103，且在5%显著水平下均显著，从而表明燃油期货市场收益率呈现出左偏厚尾分布特征。又从表1中结果可知，LB（7）值为27.9968，且在1%显著水平下显著，表明燃油期货市场收益波动率序列存在自相关性；对于ARCH效应检验而言，从表1中可以得出，燃油期货市场收益率序列显著存在ARCH效应。通过上述分析可知，油期货市场收益波动率分布呈现出了尖峰左偏、非对称等“典型事实特征”，而GJR模型恰能有效地刻画出燃油期货市场收益波动率的这些“典型事实特征”。此外，GJR模型还能够刻画金融市场收益波动所呈现出的杠杆效应，进而能够对燃油期货市场波动率进行更加有效的刻画。因此，本文基于GJR模型对燃油期货市场波动率进行研究。

（二）模型参数估计结果及分析

本文不仅对两状态以及三状态下的HMM-GJR模型参数进行了估计，而且还估计GJR模型参数，进而对比分析多波动状态下模型参数表现出的燃油期货市场特征（见表2）。

通过对表2中模型参数的分析，可以直观地得出，HMM-GJR模型在不同波动状态下及中国燃油期货市场在不同状态下收益率均值u均不为0，且具有较为明显的差异，从而说明中国燃油期货市场表现出了明显的多波动状态，也间接表明对燃油期货市场进行多波动状态研究的必要性。

进一步分析表2中各模型参数可知，参数β估计值都比较大且显著大于零，表明燃油期货市场波动率具有较强的波动持续性，进而也表明燃油期货市场波动状态不仅受当期市场信息的影响，而且还受前期波动状态的影响，也间接证明了HMM-GJR模型能够对燃油期货市场波动率进行有效地刻画；而参数γ估计值均为负且均显著，表明燃油期货市场波动率具有显著的“负杠杆效应”，即等量“利空消息”要比等量“利好消息”对能源期货市场产生更强的影响，且与“HMM模型能够更有效地对燃油期货市场高波动状态进行预测”这一结论相互论证，从而间接表明了HMM-GJR模型对燃油期货市场波动率预测的准确性。

此外，对比表2中各模型下似然值、AIC以及BIC值可发现，HMM（2）-GJR模型比其他模型具有更高的似然值，以及更低的AIC与BIC值，因而表明HMM（2）-GJR模型对燃油期货市场收益率具有更强的拟合性，同时也说明燃油期货市场表现出了较为明显的两种波动状态，从而证明HMM（2）-GJR模型能够更有效地刻画燃油期货市场波动率。

为了能够更加充分地证明HMM（2）-GJR模型对燃油期货市场波动率描述的准确性，本文还给出燃油期货市场收益率及其波动状态（见图1）。

对图1分析可知，燃油期货市场收益率波动幅度的变化趋势与其波动状态几乎一一对应，从而表明HMM模型能够较好地刻画出燃油期货市场的多波动状态。尤其需要指出的是，HMM模型对燃油期货市场收益波动幅度变化较大且比较集中的收益率波动状态的描述更加灵敏，从而表明HMM模型能够适用于金融危机或金融波动较为明显的金融市场的风险预警。

综上所述，HMM模型能够有效地刻画出燃油期货市场波动状态，且呈现出了明显的高、低两种波动状态；再有，HMM（2）-GJR模型对燃油期货市场收益波动率具有更强的拟合性。

（三）燃油期货市场VaR风险测度结果及分析

由上述分析可知，HMM模型能够有效地刻画出燃油期货市场波动状态。但还需进一步来探究引入了隐马尔科夫模型的HMM-GJR模型是否能够提高燃油期货市场VaR风险测度的准确性（见图2）。

通过对图2分析可得，两模型下的VaR风险值在某些时间段内表现出相似的变化趋势，但基于HMM-GJR模型下VaR风险值的波动程度强于GJR模型下VaR风险值的波动程度，且与其收益波动率的变化趋势更加一致。可能是因为，中国燃油期货市场由于自身不完善的风险管理制度以及金融危机的影响而出现了结构突变现象，从而导致其收益率呈现出高、低波动状态，进而使得VaR风险值也表现出更强的波动性，因而与其收益波动率具有更加相似的变化趋势。因此，HMM-GJR模型下VaR测度方法能够更准确测度出燃油期货市场风险。

（四）风险测度模型的可靠性检验

对模型的检验，就是将所得的VaR风险测度的检验P 值与设定的显著水平进行比较。若p值大于设置的显著水平，则表明该风险测度模型通过了检验；反之，则未通过检验（见表3）。

从表3中的检验结果可以直观地看出，在GJR模型下VaR风险测度没有通过检验。可能是因为，燃油期货市场受到金融危机等因素的严重冲击而出现结构突变，进而其波动率呈现出了多波动状态，而单机制的GJR模型由于不能有效地描述多波动状态下燃油期货市场波动率，从而使得基于单机制的GJR模型下VaR风险测度不能有效反映出燃油期货市场的实际风险。而HMM-GJR模型下燃油期货市场VaR风险测度都通过了检验，也再次证明HMM（2）-GJR模型对燃油期货市场波动率刻画的准确性。同时，由风险测度模型的检验原理可知，检验p值越大，表示模型越可靠。根据表3的检验结果可知，在97.5%的显著水平下基于HMM（2）-GJR的VaR方法能够更有效地对燃油期货市场进行风险测度。

五、结论

由于中国燃油期货市场呈现出多波动状态的特征，本文先引入HMM模型对其进行波动状态刻画，进而使用了HMM-GJR模型对结构突变现象下中国燃油期货市场收益波动率进行刻画，最后对燃油期货市场进行VaR风险测度，并应用Back-testing方法检验风险测度模型的可靠性。研究结果表明：中国燃油期货市场表现出了模型的高、低两种波动状态，且HMM模型对高波动状态的刻画具有显著的优越性；HMM（2）-GJR模型能够准确描述燃油期货市场收益波动率；基于HMM（2）-GJR模型下的燃油期货市场VaR风险测度更加可靠。

【参考文献】

[1] Glosten，L. R&R. Jagannathan & D. E. Runkle. On the relation between the expected value and the volatility of the nominal excess return on stocks[J]. The Journal of Finance，1993，48（5）：1779-1801.

[2] Yuan，C. M. Forecasting exchange rates： The multi-state Markov-switching model with smoothing[J]. International Review of Economics & Finance，2011，20（2）：342-362.

[3] Rabiner，L&B. H. Juang. An introduction to hidden Markov models[J]. ASSP Magazine，IEEE，1986，3（1）：4-16.

[4] Eddy，S. R. Hidden markov models[J]. Current opinion in structural biology，1996，6（3）：361-365.

[5] Chong，W&N. Reymer. Online Detection of Markov Switching Models[Z].2012-04-30.

[6] 淳伟德，陈王，潘攀.典型事实约束下的上海燃油期货市场动态VaR测度研究[J].中国管理科学，2013，21（2）： 24-31.

[7] 王鹏，魏宇.中国燃油期货市场的VaR与ES风险度量[J].中国管理科学，2012，20（6）：1-8.

[8] Christoffersen，P. F. Evaluating interval forecasts[J]. International Economic Review，1998，39（4）：841-862.