融合K均值分簇MST路由的无线传感网压缩采样技术*
2015-08-17张美燕蔡文郁
张美燕,蔡文郁
(1.浙江水利水电学院电气工程系,杭州310018;2.杭州电子科技大学电子信息学院,杭州310018)
融合K均值分簇MST路由的无线传感网压缩采样技术*
张美燕1,蔡文郁2*
(1.浙江水利水电学院电气工程系,杭州310018;2.杭州电子科技大学电子信息学院,杭州310018)
考虑无线传感网中数据采集特点和能量约束性,将分簇路由策略融合到压缩感知采样中,提出了一种融合K均值分簇MST路由的压缩采样算法。算法采用稀疏投影矩阵以减小投影矩阵与稀疏基之间的相关度,利用K均值分簇MST(Minimum Spanning Tree)机制构造数据融合树,在保证数据重构质量的基础上减少网络数据传输量。仿真结果表明,算法可以提高网络能量使用效率,同时可以适应各种规模的无线传感网。
无线传感网;压缩感知;自适应采样;最小生成树;K均值分簇
EEACC:6150Pdoi:10.3969/j.issn.1004-1699.2015.09.023
作为无线传感网的最重要和最基本的功能,网内数据采集技术得到了广泛研究[1]。由于网内传感数据存在着较强的时空相关性,直接传输原始数据显然并不合适,很多研究采用了传统的压缩编码技术以尽量减少需要传输的数据量。近年来,压缩感知技术[2-4]作为一种全新的信息采集与处理的理论框架,立刻引起了研究者的广泛关注。压缩感知借助信号内在的稀疏性或可压缩性,可从小规模的线性、非自适应的测量中通过非线性优化的方法重构信息,在降低采样频率的同时还能实现采样与压缩同步并行。压缩感知理论表明:只要信号在某个变换域是稀疏的或可压缩表示的,就可用与稀疏基不相关的测量矩阵将该高维信号投影到低维空间,通过求解一个非线性最优化问题,可重构出原始信号。压缩感知为解决传统Shannon-Nyquist采样方法面临的高成本、低效率、信息冗余以及数据传输的资源浪费等问题带来了新的契机。最近研究表明,压缩感知理论充分发掘了无线传感网内信号的内相关性和互相关性,提高了网内分布式数据采集的重构性能和压缩比。因此,将压缩感知理论应用于无线传感网,可以用较低速率对信号进行采样,同时并行地对信号进行压缩处理,即在采样的过程中寻找最少的系数来表示全部信号,并用适当的重构算法从压缩数据中恢复原始信号。
若采用传统的无线传感网数据收集方法,越接近Sink节点的节点需要转发越多下游节点的数据,形成“hot spot”现象,严重影响网络性能。本文结合无线传感网的分层最短生成树(MST)路由技术与压缩感知技术,借鉴混合压缩感知(Hybrid-CS)的思想,提出一种基于分层最短路径树的稀疏随机投影算法,通过将数据融合树与压缩感知技术相结合,实现无线传感网内数据的高效采集与传输。
1 相关文献
压缩感知理论(CS,Compressed Sensing)[2-4]突破了奈奎斯特均匀采样定理的限制,信号的带宽不再由采样速率来决定,而是由信息在信号中的结构和内容决定。CS编码的计算复杂度比较低,只需要在某个随机观测矩阵上对信号进行线性投影,就可以得到压缩之后的观测向量,编码与解码之间相对独立,在编码端采用相同的编码方案,而在解码端可以采用不同的解码技术。因此,CS理论的这些优点特别适合资源受限的分层无线传感网,只要传感器节点的数据能够在某些正交基上对该信号进行稀疏表示,在各个簇头节点运行具有较低复杂度的编码算法得到观测向量,汇聚节点在收集到节点感知数据的观测向量后,运行比较复杂的CS解码算法进行重构,这样传感器节点之间不用进行数据交换也可实现对感知数据的压缩及重构,明显地减少了网络的开销。文献[5]将CS理论应用于无线传感网的数据收集,并取得了较为显著的数据压缩效果。文献[6-8]将压缩感知技术应用到大规模无线多跳传感器网络进行分布式数据收集,结果证明该技术能有效地减少网络通信量。文献[9]提出了CDG (Compressive Data Gathering)方法,通过线性运算将N个传感器节点的数据从N维空间映射到M(M<N)维空间,从而减少数据传输量。文献[10]更是将压缩感知应用到了传感数据的差错检测中。
目前,研究者分别提出了基于簇的数据收集协议[11]、基于链的数据收集协议[12]和基于树的数据收集协议[13-14],其目标是建立一种底层的拓扑结构,以有效利用节点能量资源。然而这些方法都无法克服数据收集所形成的“热区”现象,即越靠近基站的节点需要承担越多的数据转发量,加快了能量消耗,缩短了网络生命周期。分布式压缩感知DCS[15]将单信号的压缩感知扩展到信号群的压缩采样,着重研究如何利用信号内相关性和互相关性对多个信号进行联合重构,大大减少了观测数量。DCS理论为分布式信号处理提供了新的方法,但是如何将其扩展到各种复杂的应用中仍是一个难题。文献[16]提出了融合函数的方法获取采样数据,但是融合函数仅能得到采集数据的统计量,而无法还原原始数据。综上所述,以上方法从不同角度研究了压缩感知技术在无线传感网中的应用,但是没有综合考虑传感器网络中资源受限节点的协作特性与网络多跳协同传输特性,距离实际的应用还有较大的距离。最新的文献[17]提出了一种方法,联合考虑随机路径(Random Walk)和压缩感知的融合,但是缺乏普适性和高效性。
2 基于分布式传感网的压缩感知技术
与传统的Shannon-Nyquist采样相比,压缩采样以低采样率直接感知具有稀疏或可压缩性的对象,而不是先以高速率进行采样,然后再对数据进行压缩,因此避免了无谓的数据采样,节省了能耗。在真实的无线传感网中,感知数据并非是稀疏信号,但是可以找到一个合适的表示基ψT,使得其稀疏信号。压缩采样技术原理如图1所示,基于分布式压缩采样的传感数据高效收集机制假设N个传感器节点的感知数据X是K稀疏的(K<<N)。这个N维稀疏信号可以从一个很小数目的非自适应随机线性投影中精确恢复。由于ℓ1范数是凸函数,所以信号重构的最优化问题是一个线性优化的问题,可以通过局部最优的贪婪迭代算法来解决。
投影后的测量值向量公式为:
Y=ΦΘ=ΦΨTX=AcsX(1)
其中Φ是观测矩阵,Ψ是正交基,Θ是信号变换后得到的稀疏系数向量,Acs=ΦΨT。
通过以下L-1范数能够高概率地精确重建稀疏向量,从此变成了一个凸优化问题,从而转化为一个求解线性规范的问题,可得恢复被压缩的信号公式为:
X*=argzmin‖‖Z1,s.t,Y=AcsZ(2)

图1 压缩感知原理示意
如图2所示的无线多跳链路式拓扑网络,可以解释无线传感网中基于压缩采样的无线多跳数据采集机制,相比较于传统的无线多跳数据传输模式,汇聚节点不是接收单个节点的感知数据,而是接收所有节点的感知数据的权值之和。在这种数据收集策略下,所有节点发送的数据包数量是相同的,从而不会产生越靠近汇聚节点的节点会优先耗费完能量的情况。将压缩感知应用于无线传感网多跳中继通信的数学模型表达式如式(3)和式(4)所示。
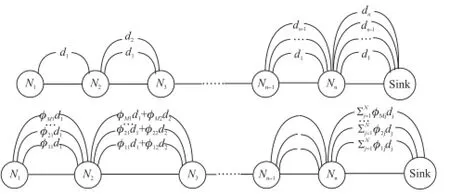
图2 基于压缩采样的无线多跳数据采集机制

基于压缩感知额数据恢复过程实质上式对可压缩信号所对应的稀疏信号s进行恢复,而并非直接恢复感知数据x。稀疏信号s可以被恢复是因为每一个测量值yi包含了一部分s的信息,即每一个压缩感知的测量值是稀疏信号s的一个线性组合值。然后,x中的每一个分量也是其对应稀疏信号s的一个线性组合。
研究表明,随机观测矩阵能以很大的概率同时满足观测矩阵与基矩阵的不相关性和可重构性,因此实际中一般采用随机矩阵进行观测,有以下定理:给定信号X∈RN,其稀疏基对应的稀疏序列S=ΨX是K稀疏的,如果测量值的个数M满足: M≥C·K·log(N/K),其中C为正常数,则信号可以被高概率恢复。根据上述压缩感知理论,观测值数目需要大于某个与稀疏度相关的最小观测值门限,才能精确重构原始信息。
3 融合K均值分簇MST路由的压缩采样
根据压缩感知理论,每个压缩感知测量值是网内所有感知数据的一个加权线性组合值。如第i个压缩感知测量值被表示为。如果测量矩阵Φ的第i行中的所有元素都为非零,则所有的节点都需要参与yi的收集。如果每一行只有一个非零的测量矩阵,而且单个测量值沿着最短路由方式传输数据,则单个测量值的传输代价可以达到最优。如图3所示。

图3 基于网络分级传输的数据聚集方式
稀疏随机投影认为对于可压缩信号进行少量的线性投影仍然可以获取该信号中的绝大部分信息,在稀疏投影过程中,参与单个测量值的传感器节点数目从稠密投影中的O(N)降到O(logN)。稀疏随机投影矩阵定义为:

其中ϕij为第i行第 j列的投影系数,Prob.为选择概率,稀疏投影矩阵的稀疏程度由参数S决定。如果ϕij≠0说明节点 j参与到第i次投影过程中,若ϕij≠0说明节点 j只负责转发来自其他节点的数据。当S=N/(logN)时,则Φ中每一行有logN个非零元素。由此可知,参与每轮数据收集的节点数至少是O(logN)。树形网络结构中各节点通过多跳的方式将自己的数据发送到汇聚节点,但是在基于压缩感知的数据收集过程中采用树形网络结构,则网络中所有节点都要参与单个测量值的收集,因此在稀疏随机投影中过多的节点参与会导致网络资源的浪费,而簇结构中簇内节点只与簇头节点进行通信,簇头与汇聚节点之间可以通过多跳方式进行通信,因此可以减少单个测量值收集过程中参与的节点数目。如图4所示。

图4 基于网络分簇结构的数据聚集方式

假设无线传感器网络集合G(V,E),将除了Sink节点之外的所有其他节点分为转发节点集FS和编码节点集CS,转发节点集只负责转发数据,编码节点集在转发数据时还进行CS压缩,假设转发节点集FS和编码节点集CS是节点集V的完全分割,因此满足:CS⋂FS=∅,CS⋃FS=V。
最优化目标定义为最小化网络中传输的数据包数量,优化模型如图5所示,其中)定义为在树t中的节点i到节点j,是否存在这样一条路径;)定义为在树t中的节点i到节点j的数据流。式(1)保证了只有唯一的一条路径通往Sink节点,式(2)保证存在这样数据流向的一个聚集树,式(3)表示只有携带正值的边才属于该聚集树,式(4)表示每一个节点都只有一条路径可到达Sink节点,寻找是一个NP-Hard问题,接下来将提出基于K均值分簇MST路由的压缩采样算法步骤。

图5 基于压缩感知的优化采样模型
本文提出算法的具体步骤如下:
①初始化,已知网络拓扑结构G(V,E),设置CS=∅,FS=V。
②利用K均值分簇MST路由传输方法建立聚类内数据最小生成树。
③对每个K均值聚类ζ内的节点,重复如下同样的操作过程:选举剩余能量最多的节点作为聚类中的簇头节点;根据式(5)获取投影矩阵Φ=[φ1φ2···φn]T,将矢量φi(1≤i≤m)中非零值所对应的节点加入编码节点集CSζ,零值所对应的节点加入转发节点集FSζ;对于编码节点集CSζ中的每个节点都设置最小生成树路由传输路径;根据式(3)沿着最小生成树进行数据收集:叶子节点将其感知的数据乘上权值发送给它的父节点,父节点负责收集所有直接子节点发来的数据并将收集齐的数据和自己感知数据的权值累加再发送给其父节点,整个收集过程以此类推。
④每个聚类的簇头节点CHζ直接将数据传输到Sink节点。
⑤Sink节点根据常规的正交匹配追踪(Orthogonal Matching Pursuit,OMP)方法进行重构。OMP是以贪婪迭代的方法选择Φ的列,使得在每次迭代中所选择的列与当前的冗余向量最大程度地相关,从测量向量中减去相关部分并反复迭代,直到迭代次数达到稀疏度K,强制迭代停止。
4 仿真结果
本文仿真场景如下:Node=100/200/300个传感器节点随机分布在100×100区域内,Sink节点位于区域中心(50,50)坐标位置,传感器节点半径为15,每次数据发送长度为512 bit,每轮随机选择比例为20%数量的节点进行数据采样传输。压缩效率定义为原始数据的矢量维度N与压缩观测矢量的维度M之比:γ=N/M,压缩效率越大说明压缩率越高。为了降低传感器节点任意分布对网络性能的影响,实验结果为50次仿真实验的平均值,每次仿真中网络拓扑结构随机生成,运行轮数Round=100-200。如图6(a)所示,利用K均值分簇算法将网络分为三个簇。压缩感知的OMP重构算法采用了文献MATLAB中的CVX工具箱[18]。仿真采用的节点能量模型如下:假设每个传感器节点的初始能量都为1 J,能量消耗模型采用常用的平方消耗模型,仿真的具体参数如下公式所示。


图6 网络拓扑K均值聚类结果图
由于平面区域内的K均值聚类可以近似包含中心节点,因此可以将Sink节点作为每个聚类的汇聚节点,K均值聚类后实现了基于最小生成树的数据传输树形成,K均值聚类最小生成树路由数据收集方式如图6(b)所示。不同数据采样长度下压缩感知数据重构效果如图7和图8所示,N取值为300,K取值为5/10/15/20/25,M取值为50/100/150/200,可见均方根误差RMSE较小,并且随着稀疏度的提高,均方根误差会逐渐增大。根据前述压缩感知理论,观测值数目需要大于某个与稀疏度相关的最小观测值门限,才能精确重构原始信息,所以可以发现当M值较小时,重构效果较差。

图7 压缩感知数据重构效果(N=300)

图8 压缩感知重构均方根误差比较(N=300)

图9 网络能量分布比较(Node=200,Round=200)
图9比较了直接汇聚传输和压缩感知传输两种情况下网络能量耗费分布,共有200个节点,仿真轮数为200轮。横坐标为剩余能量率,定义为归一化能量率,即剩余能量与初始能量比值。纵坐标为节点个数。剩余能量率高的节点越多说明网络能量效率越高,因此可见采用本文提出的压缩采样传输方式可以提高一部分的能量使用效率。
5 结语
压缩感知理论突破了奈奎斯特均匀采样定理的限制,信号的带宽不再由采样速率来决定,而是由信息在信号中的结构和内容决定。压缩感知理论的这些优点特别适合资源受限的分层结构的无线传感网,采集终端采用了复杂度较低的稀疏采样后,汇聚节点运行比较复杂的解码算法进行可接受重构,这样传感器节点之间不用进行数据交换也可实现对感知数据的压缩及重构。本文基于K均值分簇本地最小生成树路由的数据传输方式,实现了压缩感知数据采样与重构,仿真结果表明本文提出的算法明显地减少了网络的开销。下一步工作将研究无线多跳中继环境中普适性更高的数据采样与传输方案。
[1] Qian Zhihong,Wang Yijun.Internet of Things-Oriented Wireless Sensor Networks Review[J].Journal of Electronics&Information Technology,2013,35(1):215-227.
[2] 杨海蓉,张成,丁大为,等.压缩传感理论与重构算法[J].电子学报,2011,39(1):142-148.
[3] Davenport M A,Duarte M F,Eldar Y C,et al.Introduction to Compressed Sensing.Compressed Sensing:Theory and Applications [M].Cambridge:Cambridge University Press,2012.
[4] Luo C,Wu F,Sun J,et al.Efficient Measurement Generation and Pervasive Sparsity for Compressive Data Gathering[J].IEEE Transactions on Wireless Communications,2010,9(12):3728-3738.
[5] Tang Yu,Zhang Bowu,Jing Tao,et al.Robust Compressive Data Gathering in Wireless Sensor Networks[J].IEEE Transactions on Wireless Communications,2013,12(6):2754-2761.
[6] 王泉,张纳温,张金成,等.压缩感知在无线传感器网络数据采集中的应用[J].传感技术学报,2014,27(11):1562-1567.
[7] Wang J,Tang S,Yin B,et al.Data Gathering in Wireless Sensor Networks Through Intelligent Compressive Sensing[C]//Proceedings of IEEE INFOCOM,Orlando,FL,March 25-30,2012:603-611.
[8] 陈正宇,杨庚,陈蕾,等.基于压缩感知的WSNs长生命周期数据收集方法[J].电子与信息学报,2014,36(10):2343-2349.
[9] Zheng Haifeng,Xiao Shilin,Wang Xinbing,et al.Capacity and Delay Analysis for Data Gathering with Compressive Sensing in Wireless Sensor Networks[J].IEEE Transactions on Wireless Communications,2013,12(2):917-927.
[10]Chun T C,Aleksandar I,Wen H.Efficient Computation of Robust Average of Compressive Sensing Data in Wireless Sensor Networks in the Presence of Sensor Faults[J].IEEE Transactions on Parallel and Distributed Systems,2013,24(8):1525-1534.
[11]刘亚,刘功亮,康文静.压缩感知和LEACH结合的水下传感器网络信息采集方案[J].传感技术学报,2013,26(3):388-395.
[12]Durmaz Incel O,Ghosh A,Krishnamachari B,et al.Fast Data Collection in Tree-Based Wireless Sensor Networks[J].IEEE Transactions on Mobile Computing,2012,11(1):86-99.
[13]Ebrahimi D,Assi C.A Distributed Method for Compressive Data Gathering in Wireless Sensor Networks[J].IEEE Communications Letters,2014,18(4):624-627.
[14]黄海平,陈九天,王汝传,等.无线传感器网络中基于数据融合树的压缩感知算法[J].电子与信息学报,2014,36(10):2364-2369.
[15]吕方旭,张金成,石洪君,等.WSN中的分布式压缩感知[J].传感技术学报,2013,26(10):1446-1452.
[16]Chen Zhengyu,Yang Geng,Chen Lei,et al.Data Aggregation Scheduling with Guaranteed Lifetime and Efficient Latency in Wireless Sensor Networks[J].China Communications,2012,9 (9):11-21.
[17]Haifeng Z,Feng Y,Xiaohua T,et al.Data Gathering with Compressive Sensing in Wireless Sensor Networks:A Random Walk Based Approach[J].IEEE Transactions on Parallel and Distributed Systems,2015,26(1):35-44.
[18]Grant M,Boyd S.CVX:MATLAB Software for Disciplined Convex Programming[BL/OL]http://cvxr.com/cvx/,2015.

张美燕(1983-),女,讲师,从事无线传感网络、新型能源技术、物联网技术等研究,主持浙江省自然科学基金1项,浙江省公益性行业专项1项,浙江省水利厅科技项目1项,参与浙江省厅级项目多项。近年来发表论文20余篇,被三大索引收录近10篇,申请发明专利和实用新型专利10余项;

蔡文郁(1979-),男,博士,副教授,主要从事无线通信、物联网、无线传感网及嵌入式技术研究。主持和参与国家自然科学基金2项、浙江省自然科学基金3项、浙江省公益性行业专项2项,国家863计划项目2项、国家海洋局行业专项1项、浙江省重大科技专项1项,横向课题10余项。近年来发表论文40余篇,被SCI/EI收录20余篇,申请专利及软著40余项,授权30余项,dreampp2000@163.com。
Compressed Sensing Technology Combined with K-Means Clustered MST Routing for Wireless Sensor Networks*
ZHANG Meiyan1,CAI Wenyu2*
(1.School of Electrical Engineering,Zhejiang University of Water Resources and Electric Power,Hangzhou 310018,China)2.School of Electronics&Information,Hangzhou Dianzi University,Hangzhou 310018,China)
Considering the special characteristics of data collection and energy constraints of wireless sensor networks,the paper combines clustered routing strategy with compressed sensing data collection method and then proposes a compressed sensing based compressive sampling algorithm with K-Means clustering MST(Minimum Spanning Tree)routing.The proposed algorithm uses the sparse projection matrix in order to reduce the correlation degree value between the projection matrix and sparse matrix so as to reduce the amount of data transmission in the basis to ensure the quality of the data reconstruction by using K-Means clustering MST data fusion tree.The simulation results show that this algorithm can improve the network energy usage efficiency,and also be suitable to all kinds of scale wireless sensor networks.
wireless sensor networks;compressive sensing;adaptive sampling;minimum spanning tree;K-Means clustering
TP393
A
1004-1699(2015)09-1402-06
项目来源:浙江省自然科学基金项目(LY15F030018,Y16F030018);国家自然科学基金项目(61102067)
2015-04-26修改日期:2015-06-10
