变体飞行器连续平滑切换LPV控制

江未来，董朝阳，王 通，王 青

（1．北京航空航天大学航空科学与工程学院，北京100191；2．北京航空航天大学自动化科学与电气工程学院，北京100191）

变体飞行器连续平滑切换LPV控制

江未来1，董朝阳1，王 通2，王 青2

（1．北京航空航天大学航空科学与工程学院，北京100191；2．北京航空航天大学自动化科学与电气工程学院，北京100191）

针对一类翼展可变飞行器的控制问题，提出了一种连续平滑切换线性变参数（linear parameter varying，LPV）控制器的设计方法。将变体飞行器建模成以翼展变形率为时变参数的LPV系统，通过对时变参数进行具有重叠特性的区间划分，设计平滑切换控制器。结合参数依赖的多李雅普诺夫函数和平均驻留时间方法，给出了保证切换LPV系统指数稳定的充分条件。由于考虑了时变参数的渐变特性，使得系统的切换律没有平均驻留时间的限制，降低了结论的保守性。仿真结果表明，运用所设计的控制器，当翼展连续变化时，变体飞行器状态稳定且切换过程平滑，控制性能良好。

变体飞行器；线性变参数系统；平滑切换；平均驻留时间；多李雅普诺夫函数

0 引 言

变体飞行器的外形结构可随飞行任务和环境自适应变化，使飞行器保持在最优飞行状态，大幅提高飞行性能并适应多种任务模式［1］。作为一类极具发展潜力的现代高性能飞行器，变体飞行器的分析与设计已成为国内外航空航天领域的研究热点。

飞行器在飞行过程中的结构变形会带来重心位置、转动惯量、机翼展长、机翼面积等构型参数的变化，从而会引起飞行器气动力与力矩、惯性力与力矩等气动特性的非线性变化。这将使得在飞行过程中进行结构变形的飞行器是一个依赖于外形结构的复杂时变非线性系统。

切换线性变参数（linear parameter varying，LPV）系统理论作为处理这类复杂时变非线性系统的有效方法，得到了诸多学者的关注［2－4］。文献［2－3］基于参数依赖多Lyapunov函数方法，研究了LPV系统的切换控制，给出了滞后切换和平均驻留时间切换2种切换律下保证系统稳定和鲁棒性能的控制器设计方法，并将其应用于主动磁浮轴承和F－16飞机进行了仿真验证。文献［4］基于混合多Lyapunov函数方法，研究了切换LPV系统的L－2诱导范数问题，并将所提方法应用于F－16的姿态控制，取得良好效果。

同时，为抑制系统在切换过程中产生的瞬态响应，提升控制性能，众多学者开展了平滑切换LPV控制的研究［5－7］。文献［5］研究了输入输出受限情形下，LPV系统的平滑切换增益调参控制问题。文献［6］将平滑切换控制器设计问题转换成一组非线性矩阵不等式的可行解求解问题，运用下降迭代算法对该问题进行寻优，得到平滑切换控制器并进行了仿真验证。文献［7］基于鲁棒控制和LPV系统理论，考虑了在常值Lyapunov函数和参数依赖的Lyapunov函数2种方法下，系统的平滑切换输出跟踪控制问题。

然而，在已有文献中，或是未讨论连续切换情形下的平滑切换控制器设计［5］，或是基于单一的参数依赖Lyapunov函数进行系统稳定性分析［6］。即便是基于参数依赖的多Lyapunov函数方法进行切换LPV系统稳定性分析时，也未考虑时变参数的渐变特性，对Lyapunov函数矩阵的约束具有较大的保守性［2－3］。针对切换LPV系统，设计连续平滑切换控制器，并研究其在变体飞行器上的应用，鲜有报道。

本文针对一类翼展可变飞行器控制问题，提出了一种连续平滑切换LPV控制器的设计方法。将变体飞行器建模成以翼展变形率为时变参数的LPV系统，并对时变参数进行具有重叠特性的区间划分，通过重叠子系统控制器由相邻2个独立子系统控制器插值的方法，得到整个系统平滑切换控制器。结合参数依赖的多Lyapunov函数和平均驻留时间方法，给出了保证切换LPV系统指数稳定的充分条件。考虑时变参数的渐变特性，得到了没有平均驻留时间限制的切换律，降低了结论的保守性。仿真结果验证了所提方法的有效性。

1 翼展可变飞行器LPV模型

考虑以Navion L－17为本体的翼展可变飞行器［8－9］，如图1所示。飞行器2侧机翼能够对称地伸缩，可达到的最大翼展是本体翼展的2倍。定义翼展变形率η＝Δb／b，式中Δb为翼展变形量，b为本体翼展，可知η∈［0，1］。本文只考虑飞行器纵向运动，且忽略外部干扰，选取飞行器在高度h＝1 524m，以马赫数Ma＝0．1做水平无侧滑匀速平飞为待研究的目标运动过程。

图1 翼展可变飞行器

在气流坐标系中，变体飞行器纵向运动非线性模型［9］为

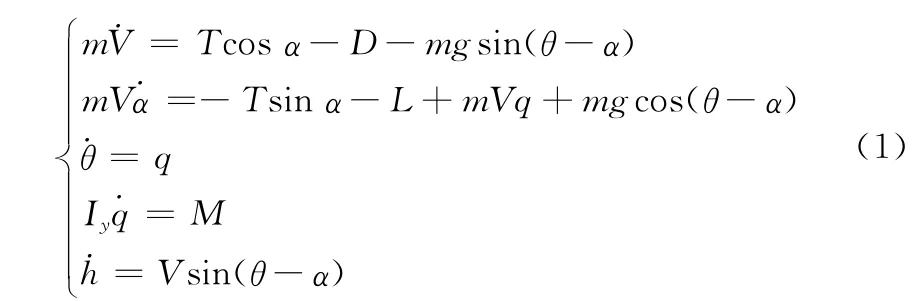
式中，θ为俯仰角；q为俯仰角速度；Iy为俯仰转动惯量；L，D，M，T分别为升力、阻力、俯仰力矩及推力，且满足

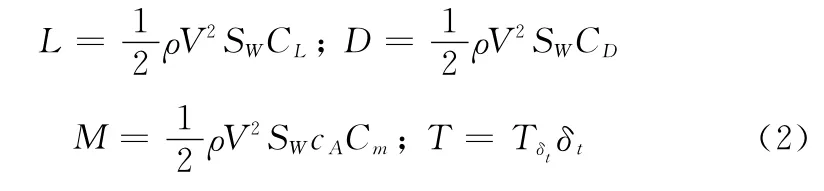
式中，SW为机翼面积；cA为平均气动弦长；ρ为大气密度；Tδt为推力系数；δt为油门开度。CL为升力系数；CD为阻力系数；Cm为俯仰力矩系数。CL，CD及Cm与迎角α、升降舵偏角δe的函数关系可近似地表示为

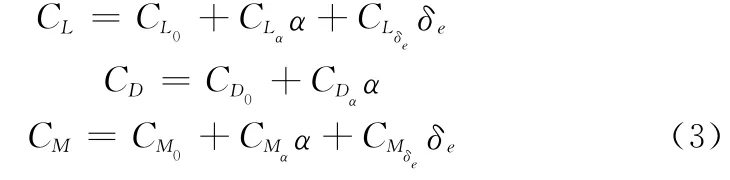
式中，α∈［0，10°］，δe∈［－40°，40°］。

借助相关软件及插值和线性拟合方法，可得到飞行器气动参数与翼展变形率之间的关系［9］为

式中，各气动导数的单位为1／（°）。

目前，将系统非线性模型转化为LPV模型主要有3种方法，分别为雅克比线性化、状态变换和函数替换［10］。在此选用最为常用的雅克比线性化方法，其思路可概述为将系统非线性模型在所选取的不同平衡点处分别线性化，并对所得到的一组线性化模型进行插值运算，即可得到系统的LPV模型。

根据上述思路，并考虑到平衡点的迎角都很小，可构建出变体飞行器纵向运动LPV模型［9］

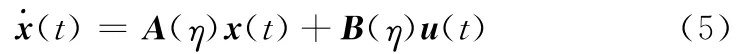
式中，状态变量x＝［ΔVΔαΔθΔqΔh］T；输入变量u＝［ΔδeΔδt］T；且

2 区间划分与控制器设计

2．1 具有重叠特性的时变参数区间划分

考虑如下所示的LPV系统

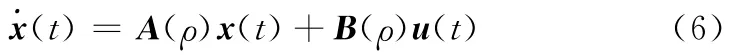
式中，x（t）∈Rn为状态向量；u（t）∈Rr为输入变量；ρ∈R为时变参数且实时可测；系数矩阵A，B为ρ的函数。假定ρ及其变化率有界

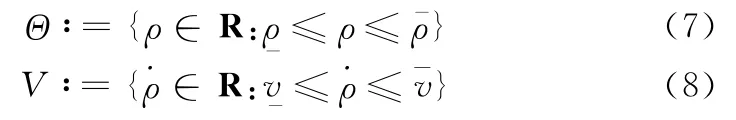
如图2所示，对时变参数进行具有重叠特性的区间划分，即将ρ的取值区间Θ划分为J个子区间，且相邻2个子区间具有重叠部分。

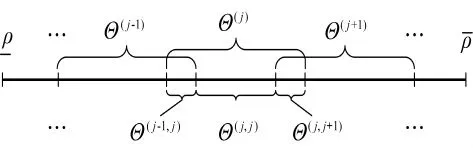
图2 具有重叠特性的时变参数区间划分

第j个子区间Θ（j）可表示为

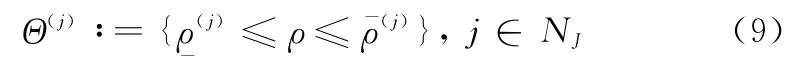
式中，NJ：＝｛1，…，J｝。定义第j个和第j＋1个子区间重叠的部分为重叠子区间Θ（j，j＋1），可表示为

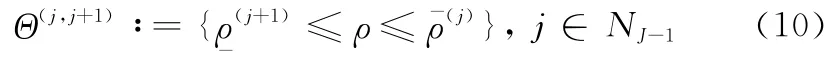
式中，NJ－1：＝｛1，…，J－1｝。

定义每一子区间去除重叠子区间以外的区间为独立子区间，可表示为

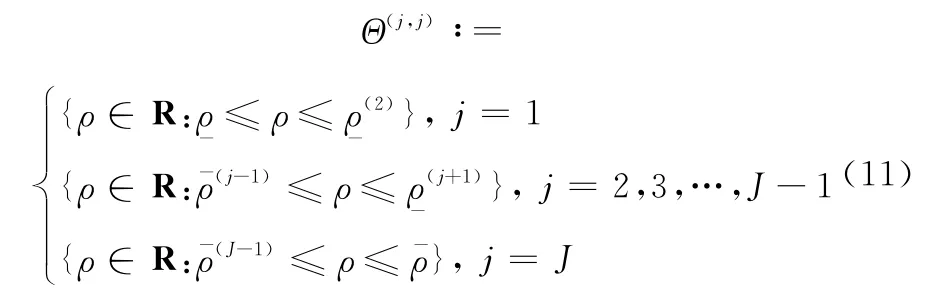
2．2 平滑切换控制器设计

如图2所示，对应于J个子区间，可得到J个LPV子系统，定义切换律，则得到开环切换LPV系统为

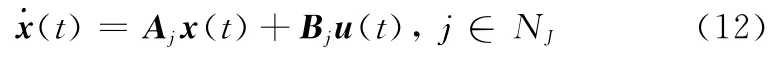
为便于书写，将子系统系数矩阵Aj（ρ），Bj（ρ）表示成Aj和Bj，下文中所有参数依赖的矩阵或矩阵变量均采用类似表达。

针对系统式（12）中的每一个子系统，设计参数依赖的无记忆状态反馈控制器：

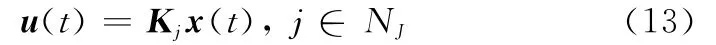
得到闭环LPV子系统

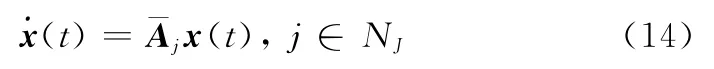
引理1［5］考虑闭环子系统式（14），时变参数及其变化率满足式（7）和式（8）。对于给定的标量β＞0，当存在适维矩阵Pj＝＞0，满足

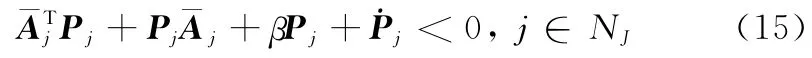
那么，闭环子系统渐近稳定。

定义Qj＝，Yj＝KjQj，则式（15）可写成参数依赖矩阵不等式

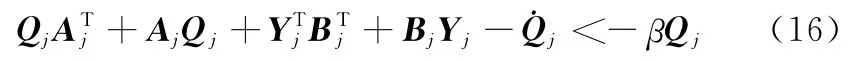
若该矩阵不等式有可行解，则状态反馈控制器的增益矩阵为

为了抑制在切换过程中产生的瞬态响应，提升系统的控制性能，设计一种具有平滑切换特性的控制器K：当ρ∈Θ（j，j）时，独立子系统控制器为Kj，j＝Kj；而当ρ∈Θ（j，j＋1）时，重叠子系统控制器为Kj，j＋1，Kj，j＋1是由相邻2个子系统上的控制器Kj，Kj＋1插值得到。即具有平滑切换特性的控制器可表示为

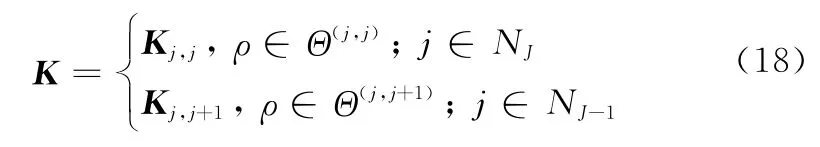
式中

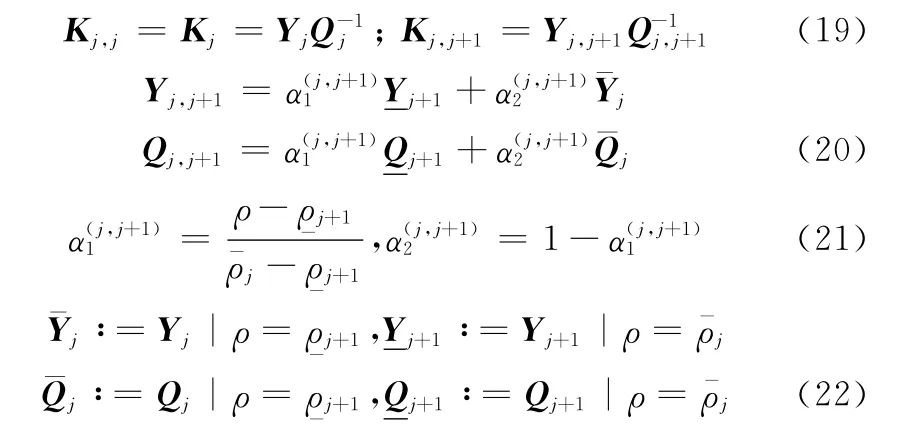
3 稳定性分析

具有重叠特性的区间划分方法，也可看作是将时变参数区间划分为2J－1个子区间，设计式（18）所示平滑切换控制器，就将LPV系统（6）转化为由2J－1个子系统及切换律构成的闭环切换LPV系统。定义σ（t）∶［t0，∞）→Ω＝｛1，2，…，2J－1｝为系统的切换律，Ω为LPV子系统集。本文中，切换律σ（t）取决于时变参数ρ，又由式（8）可知，时变参数具有渐变特性，所以子系统间的切换仅发生在时变参数子区间的边界上。

得到闭环切换LPV系统

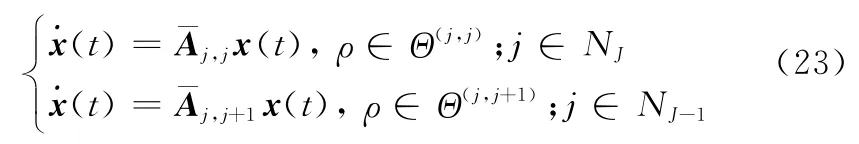
式中

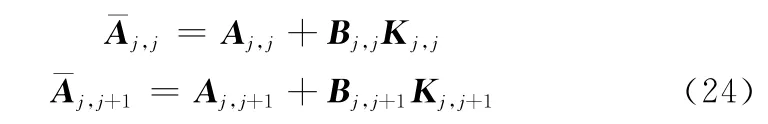
｛Aj，j，Bj，j｝，｛Aj，j＋1，Bj，j＋1｝分别为独立子区间Θ（j，j）和重叠子区间Θ（j，j＋1）上子系统的系数矩阵。

定义1［11］对于切换LPV系统（23），假设切换律σ（t）在时间段ΔT＞0内切换次数为Nσ（ΔT），对于任意N0≥0，若不等式

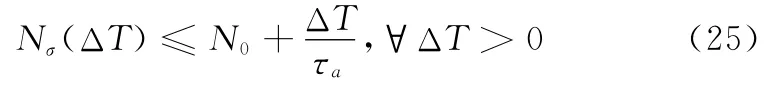
成立，那么，τa称为平均驻留时间。

定义2 如果存在切换律σ（t），使得系统的状态轨迹满足‖x（t）‖≤α‖x（t0）‖e－β（t－t0）（α≥0，β≥0，t≥t0），则称系统是指数稳定的。

定理1 考虑闭环切换LPV系统式（23），时变参数及其变化率满足式（7）和式（8）。给定标量β＞0，μ＞1，如果存在连续可微的适维矩阵Pj，j＝PTj，j＞0（j∈NJ），Pj，j＋1＝＞0（j∈NJ－1）使得表达式

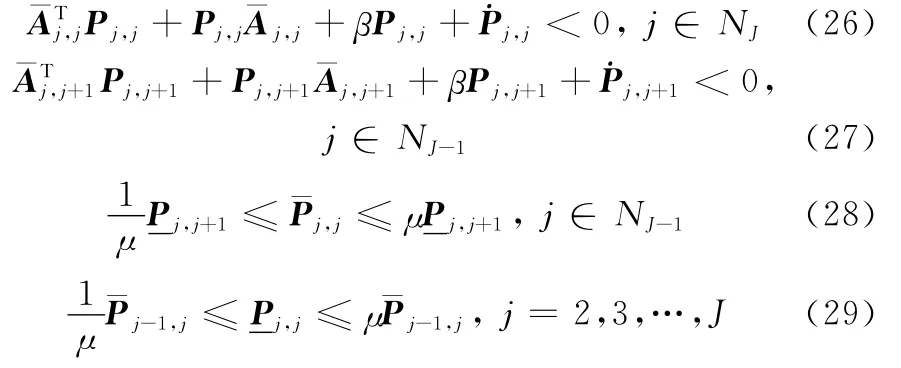
成立，其中

并且系统的平均驻留时间满足

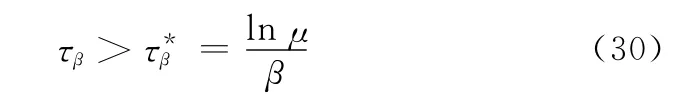
那么，系统式（23）指数稳定。

证明 首先考虑独立子区间Θ（j，j）上的闭环子系统，选取参数依赖Lyapunov函数

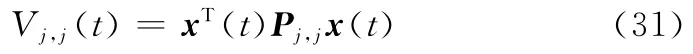
接下来，考虑重叠子区间Θ（j，j＋1）上的闭环子系统，选取参数依赖Lyapunov函数为

由式（27）有˙Vj，j＋1（t）≤－βVj，j＋1（t），即

式中，tj，j＋10表示重叠子区间Θ（j，j＋1）上的子系统运行的初始时刻。

最后，考虑在不同子系统之间切换的情形。由于切换仅发生在子区间边界上，所以由式（28）～式（29）可知，在切换时刻

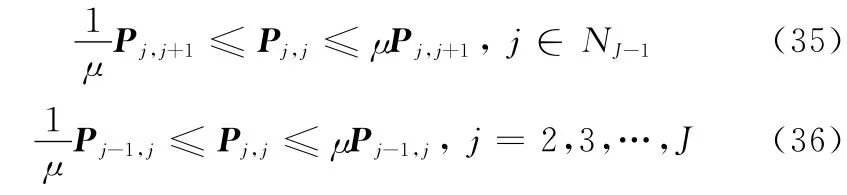
将系统的运行时间分割成［t0，t1），［t1，t2），…，［tn－1，tn），［tn，T）。不失一般性，假设时变参数ρ最近5次所处子区间及切换顺序为

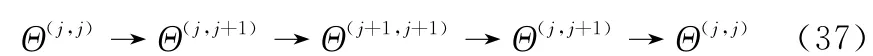
当系统运行在t∈［tk，tk＋1）时，由式（32）、式（34）～式（37）可知，系统的Lyapunov函数满足

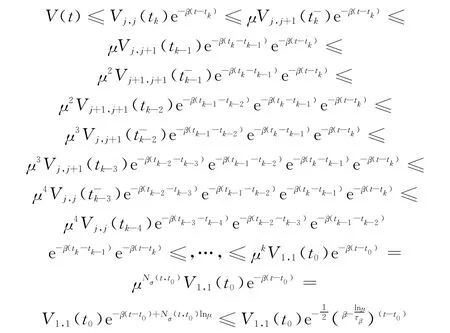
选取

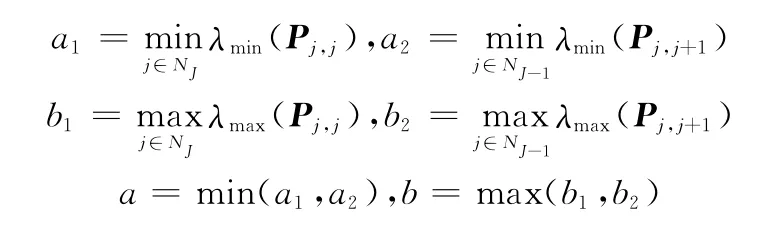
至此，基于参数依赖的多Lyapunov函数和平均驻留时间方法，得出在连续切换时，切换LPV系统式（23）指数稳定的充分条件。下面在定理1的基础上，给出平滑切换控制器的设计方法。

定理2 考虑切换LPV系统式（12），时变参数及其变化率满足式（7）～式（8），具有重叠特性的时变参数区间划分如式（9）～式（11）定义。给定标量β＞0，若存在连续可微的矩阵Qj＝＞0及矩阵Yj，使得

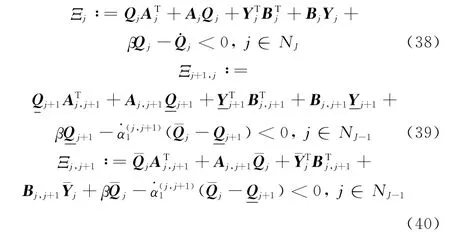
证明 首先，考虑独立子区间Θ（j，j）上的闭环子系统。其控制器

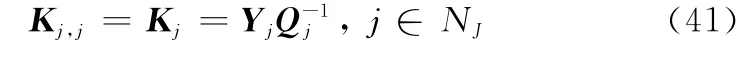
定义

可知式（38）等价于

由于独立子区间Θ（j，j）包含于Θ（j），所以由式（18）和式（43）可知式（26）成立，也即若式（38）成立，则式（26）成立。

接下来，考虑重叠子区间Θ（j，j＋1）上的闭环子系统。若式（39）～式（40）成立，则可知式（39）和式（40）的凸组合

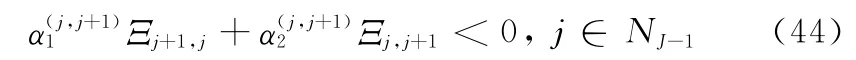
成立。结合式（20）和式（21）可知

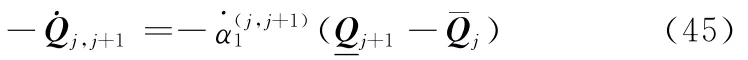
式中

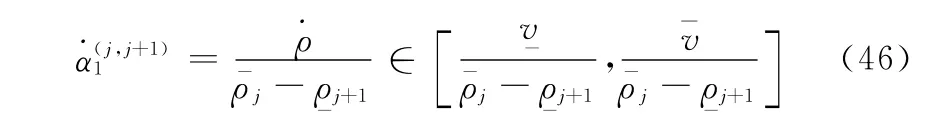
所以，式（44）等价于

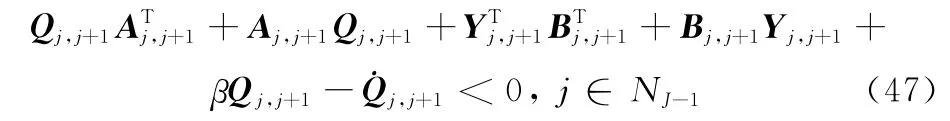
由式（18）知，在重叠子区间Θ（j，j＋1）上，Kj，j＋1＝Yj，j＋1Q－1j，j＋1（j∈NJ－1），定义

可知式（47）等价于式（27），也即若式（39）～式（40）成立，则式（27）成立。

最后，考虑时变参数在独立子区间和重叠子区间之间切换的情形。由定义式（42），在独立子区间Θ（j，j）对应的子系统上，Lyapunov函数矩阵

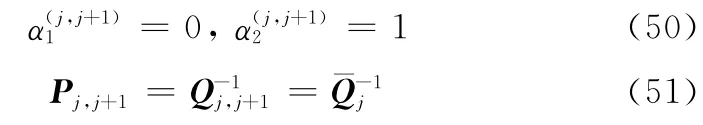
等价于式（28）和式（29）中μ＝1，由式（30）可知平均驻留时间的下界＝0。

对应于定理1，可知定理2得证。证毕

注1 由于考虑时变参数变化率有界，也即时变参数具有渐变特性，所以在定理1中，只在子区间边界上对Lyapunov函数矩阵提出了式（28）和式（29）所示的约束条件。进而在定理2中，通过式（20）所示的定义，得到了没有平均驻留时间限制的切换律，降低了结论的保守性。

注2 对时变参数进行具有重叠特性的区间划分，子区间个数及上下界的选取需综合考虑计算的复杂程度以及相对稳定裕度β的大小。可采用基于图论的随机搜索算法［12］来确定区间的划分方法。

注3 由于参数的依赖性，式（38）～式（40）对应的是无限维的线性矩阵不等式组，可采用近似基函数和网格技术将其转化为有限维的LMIs［13－14］。选取近似基函数为，则有

因此，平滑切换控制器增益矩阵可通过求解式（18）、式（38）～式（40）和式（54）得到。

4 仿真分析与验证

为验证所提方法的有效性，对式（5）所示的翼展可变飞行器LPV模型进行仿真。选取翼展变形率为时变参数，并设定

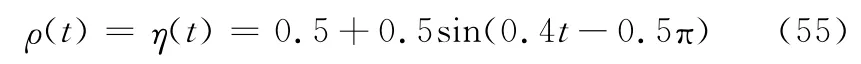
则式（7）和式（8）中Θ∶＝［0，1］，V∶＝［－0．2，0．2］。在此，将时变参数划分为具有重叠特性的3个子区间，如图3所示。

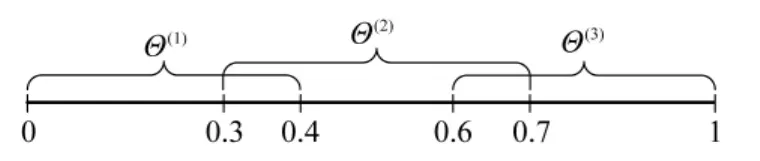
图3 翼展变形率区间划分

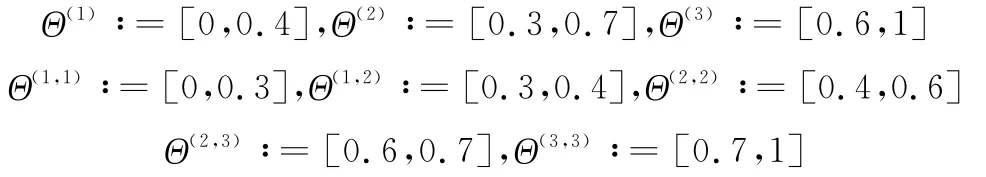
为便于计算，假定式（54）中，Qj（j＝1，2，3）为常值矩阵。选取Yj的基函数为f1＝1，f2＝ρ（t）。利用网格技术将Θ均匀划分为50个网格，选择β＝0．8，解得3个独立子系统的控制器分别为

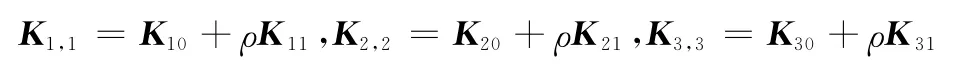
式中

由式（18）可算得2个重叠子系统的控制器，从而得到整个系统的平滑切换控制器。

运用所设计的控制器，进行变体飞行器非线性仿真。假定从第5s开始，翼展变形率η按照式（55）的规律，由0→1→0逐渐变化，如图4所示。部分仿真曲线如图5～图8所示。

图4 翼展变形率η变化曲线

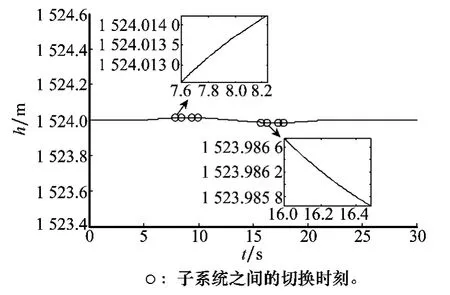
图5 飞行器高度变化曲线

图6 飞行器迎角变化曲线

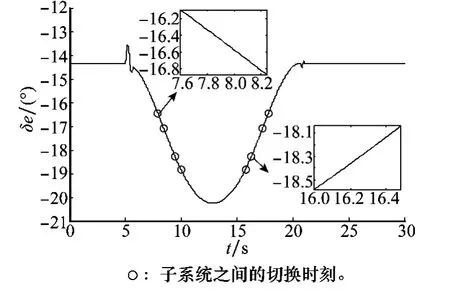
图7 升降舵舵偏变化曲线

图8 油门开度变化曲线

由图5和图6所示的飞行器高度和迎角变化曲线可知，当翼展连续变化时，飞行器高度基本保持不变，迎角缓慢变化，飞行器具有良好的稳定性。由图7和图8可知，升降舵舵偏及油门开度总体变化缓和，变化范围合理。同时，选取时变参数由Θ（1，1）→Θ（1，2）和Θ（2，3）→Θ（2，2）2个切换时刻为例，通过细节放大图可知，飞行器状态和控制输入均未出现抖动，系统切换过程平滑，控制性能良好。

5 结 论

基于切换LPV系统理论，研究了翼展可变飞行器的连续平滑切换控制问题。通过对时变参数进行具有重叠特性的区间划分，设计平滑切换控制器。由于考虑了时变参数的渐变特性，使得系统的切换律没有平均驻留时间的限制，降低了结论的保守性。仿真结果表明，运用所设计的控制器，当翼展连续变化时，变体飞行器状态稳定且切换过程平滑，控制性能良好。

［1］Rodriguez A R．Morphing aircraft technology survey［C］∥Proc．of the 45th AIAA Aerospace Sciences Meeting and Exhibit，2007：1－16．

［2］Lu B，Wu F．Switching LPV control designs using multiple parameter－dependent Lyapunov functions［J］．Automatica，2004，40（11）：1973－1980．

［3］Lu B，Wu F，Kim S W．Switching LPV control of an F－16aircraft via controller state reset［J］．IEEE Trans．on Control Systems Technology，2006，14（2）：267－277．

［4］He X，Zhao J．Multiple Lyapunov functions with blending for induced L2－norm control of switched LPV systems and its application to an F－16aircraft model［J］．Asian Journal of Control，2014，16（1）：149－161．

［5］Chen P C．The design of smooth switching control with application to V／STOL aircraft dynamics under input and output constraints［J］．Asian Journal of Control，2012，14（2）：439－453．

［6］Hanifzadegan M，Nagamune R．Smooth switching LPV controller design for LPV systems［J］．Automatica，2014，50（5）：1481－1488．

［7］Song L，Yang J．Smooth switching output tracking control for LPV systems［J］．Asian Journal of Control，2012，14（6）：1710－1716．

［8］Nelson R C．Flight stability and automatic control［M］．WCB／McGraw Hill，1998．

［9］Yin M，Lu Y P，He Z．LPV modeling and robust gain scheduling control of morphing aircraft［J］．Journal of Nanjing University of Aeronautics ＆Astronautics，2013，45（2）：202－208．（殷明，陆宇平，何真．变体飞行器LPV建模与鲁棒增益调度控制［J］．南京航空航天大学学报，2013，45（2）：202－208．）

［10］Marcos A，Balas G J．Development of linear－parameter－varying models for aircraft［J］．Journal of Guidance，Control，and Dynamics，2004，27（2）：218－228．

［11］Hou Y，Wang Q，Dong C．Gain scheduled control：switched polytopic system approach［J］．Journal of Guidance，Control，and Dynamics，2011，34（2）：623－629．

［12］Diestel R．Graph theory［M］．New York：Springer－Verlag，2000．

［13］Apkarian P，Adams R J．Advanced gain－scheduling techniques for uncertain systems［J］．IEEE Trans．on Control Systems Technology，1998，6（1）：21－32．

［14］Wu F，Grigoriadis K M．LPV systems with parameter－varying time delays：analysis and control［J］．Automatica，2001，37（2）：221－229．

E－mail：jiangweilai＠126．com

董朝阳（1966－），男，教授，博士，主要研究方向为变体飞行器建模与控制、LPV系统。

E－mail：dongchaoyang＠buaa．edu．cn

王 通（1987－），男，博士研究生，主要研究方向为飞行器控制、切换系统、鲁棒控制。

E－mail：xenon＠buaa．edu．cn

王 青（1968－），女，教授，博士，主要研究方向为导航制导与控制、智能控制。

E－mail：wangqing＠buaa．edu．cn

Continuous smooth switching LPV control for morphing aircraft

JIANG Wei－lai1，DONG Chao－yang1，WANG Tong2，WANG Qing2
（1．School of Aeronautical Science and Engineering，Beihang University，Beijing 100191，China；2．School of Automation Science and Electrical Engineering，Beihang University，Beijing 100191，China）

To cope with the control problem of a class of variable－span morphing aircraft，a continuous smooth switching linear parameter varying（LPV）controller is proposed．Choosing the rate of span variation as the time－varying parameter，the morphing aircraft is modeled as a LPV system．The smooth switching controller is designed in the way that the time－varying parameter is partitioned into several subregions with overlaps．Then，a sufficient condition to ensure the switched LPV system’s exponential stability is presented by employing the methods of multiple parameter－dependent Lyapunov functions and average dwell time．Because the character that the time－varying parameter changes gradually is considered，the switching law without constraint on average dwell time is obtained which makes the conclusion less conservative．The simulation result shows that using the proposed controller，the states of morphing aircraft are stable and switch smoothly when the span changes continuously．

morphing aircraft；linear parameter varying（LPV）system；smooth switching；average dwell time；multiple Lyapunov functions

V 249．1

A

10．3969／j．issn．1001－506X．2015．06．19

江未来（1989－），男，博士研究生，主要研究方向为变体飞行器建模与控制、切换系统。

1001－506X（2015）06－1347－07

2014－07－21；

2014－09－15；网络优先出版日期：2014－11－20。

网络优先出版地址：http：／／www．cnki．net／kcms／detail／11．2422．TN．20141120．2112．011．html

国家自然科学基金（61273083）资助课题