全仿射形变下基于点特征的SAR图像配准方法

刘永春，王广学，栗 苹，闫晓鹏

（1．北京理工大学机电工程与控制国家重点实验室，北京100081；2．空军预警学院信息对抗系，湖北武汉430019）

全仿射形变下基于点特征的SAR图像配准方法

刘永春1，王广学2，栗 苹1，闫晓鹏1

（1．北京理工大学机电工程与控制国家重点实验室，北京100081；2．空军预警学院信息对抗系，湖北武汉430019）

全仿射形变条件下，待配准合成孔径雷达（synthetic aperture radar，SAR）图像与参考SAR图像之间存在各向异性尺度变化，导致传统的点特征图像配准算法难以提取到足够多的匹配特征点进行图像配准。为此，提出了一种基于仿射形变矩阵分解与尺度变化矩阵估计的点特征图像配准算法。该方法首先将仿射形变矩阵分解为图像旋转矩阵、尺度变化矩阵以及常数矩阵的乘积，而后利用粒子群优化（particle swarm optimization，PSO）算法对尺度变化矩阵中的未知参数进行搜索估计，并根据估计结果对图像进行尺度规范处理，以抑制图像间的各向异性尺度变化，在此基础上再利用尺度不变特征转换（scale invariant feature transform，SIFT）算子提取匹配特征点进行配准处理。实验结果表明，与现有方法相比，对于全仿射形变条件下的SAR图像配准，本文所述算法可以提取到更多的匹配特征点，因而具有更好的配准性能。

合成孔径雷达图像配准；仿射变换；粒子群优化算法；尺度不变特征转换算子

0 引 言

图像配准是合成孔径雷达（synthetic aperture radar，SAR）图像处理领域的重点研究内容之一，在SAR图像变化检测、超分辨处理、图像融合等方面有着广泛的应用［1－4］。点特征是指图像中灰度值在二维方向都具有明显变化的点，如图像的角点、圆点等。由于点特征普遍存在于各类观测场景的SAR图像中，因而基于点特征的SAR图像配准方法受到广泛的关注。如文献［5］研究了基于Harris算子的点特征图像配准算法，文献［6］研究了基于Moravec算子的点特征图像配准算法，文献［7］研究了基于Forstner算子的点特征图像配准算法。上述算法的共同缺陷在于对图像尺度变化较为敏感，当参考图像与待配准图像的尺度存在较大差异时，难以获取到足够多的匹配特征点，从而导致配准失败。针对上述问题，文献［8］提出了一种基于多尺度空间的尺度不变特征转换（scale invariant feature transform，SIFT）算子，当待配准图像与参考图像间的尺度变化各向同性时，SIFT算子获取的匹配特征点数明显增加，从而提高了图像配准的可靠性。在SIFT算子提出后，引起了广泛关注，并衍生出了一系列改进算法，如PCA－SIFT算法［9］、SURF算法［10］、多尺度Harris算法等［11］。然而此类算法仅对各向同性尺度变化有效，当待配准图像与参考图像间的尺度变化在不同方向存在明显差异时，提取到的匹配特征点数亦会随之下降，从而导致配准可靠性降低，因此不适用于全仿射形变条件下的SAR图像配准。为了增加全仿射变换条件下SIFT算子获取的匹配特征点个数，文献［12］以光学成像几何模型为基础提出了一种仿射尺度不变特征转换（affine scale invariant feature transform，ASIFT）算法。然而，该算法在实现过程中需要对成像光轴经、纬角进行四维稀疏离散采样，采样误差的存在限制了算法性能的提高。此外，该算法还限定仿射形变矩阵的行列式为正，当行列式为负时，该算法与SIFT算法一样难以获得足够的匹配特征点。

鉴于以上分析，为了提高全仿射形变条件下的SAR图像配准性能，本文提出了一种基于仿射形变矩阵分解与尺度变化矩阵估计的点特征图像配准算法。该方法首先将仿射形变矩阵转化为图像旋转矩阵、尺度变化矩阵以及常数矩阵的乘积，而后对尺度变化矩阵中的未知参数取值范围进行分析，进而利用粒子群优化算法对其进行搜索估计，并根据估计结果对参考图像与待配准图像进行尺度规范处理，以抑制两者之间的各向异性尺度变化，在此基础上再利用SIFT算子提取匹配特征点进行配准处理。实验分析表明，对于全仿射形变条件下的SAR图像配准，与现有方法相比，本文算法提取到的匹配特征点明显增加，因而具有更好的配准性能。

1 仿射形变矩阵分解

记I1、I2分别为对应同一观测区域的参考SAR图像与待配准SAR图像，当I1与I2之间存在全仿射形变时，I1与I2之间的坐标变换模型可表示如下：

式中，（x1，y1）、（x2，y2）分别为观测区域内任意一点在图像I1、I2中的坐标；xoff、yoff为坐标平移参数；A为非奇异仿射形变矩阵。A的两个奇异值λ1、λ2可分别表示为

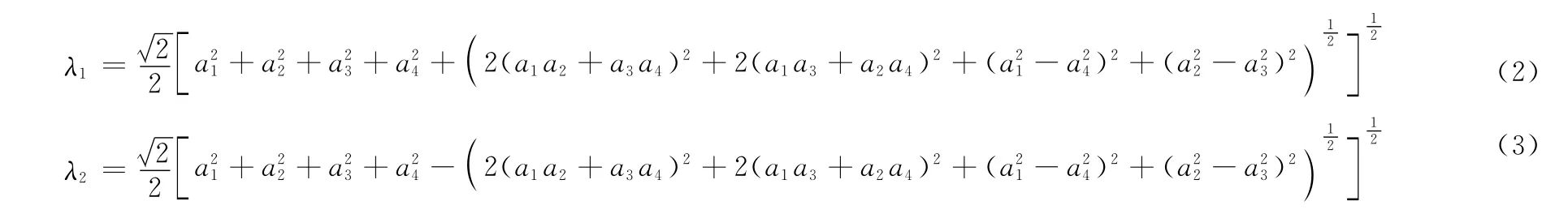
由矩阵奇异值分解的性质可知［13］，λ1、λ2分别表示I1相对于I2在一对相互垂直方向上的尺度变化值，且λ1／λ2表示I1与I2在不同方向上尺度变化值之比的最大值，即I1与I2间存在的最大各向异性尺度变化。当λ1／λ2＝1时I1与I2间的尺度变化在各个方向相等，反之则存在各向异性尺度变化，并且随着λ1／λ2的增大，尺度变化的各向异性越为明显，从而导致SIFT类配准算法失效。然而需要指出的是，尽管理论上λ1／λ2的取值可以无限大，但是随着λ1／λ2增大，也会使得图像I1与I2之间的相对失真越来越严重，从而导致配准后的图像解译处理变得愈加困难。因此，实际应用中λ1／λ2的取值通常位于一定的区间范围内，不失一般性，本文中假设λ1／λ2≤20，在此基础上，由式（2）、式（3）可得

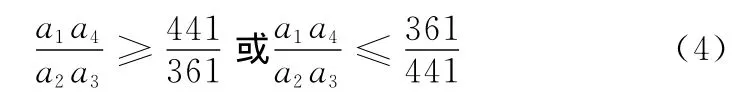
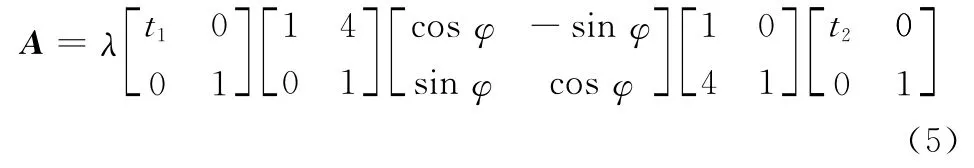
式（5）的证明可直接将式（6）、式（7）以及λ、sinθ、cosθ的计算表达式代入式（5）得到。同理可得，当且 a1、a4不同时等于0，或且a、a同时等于0时，A23可分解成如下形式：

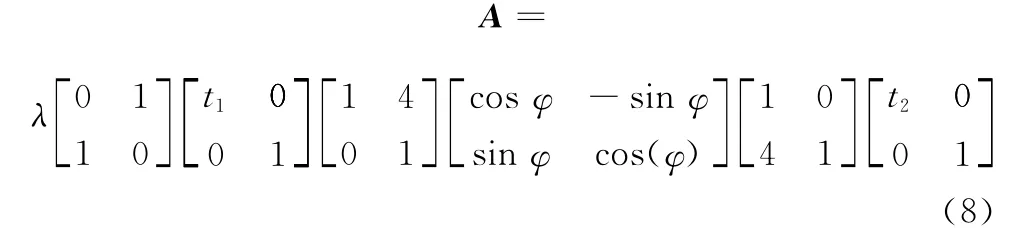
由式（5）、式（8）可知，当满足条件λ1／λ2≤20时，对于任意的仿射形变矩阵A，都可以表示为图像旋转矩阵、尺度变化矩阵以及常数矩阵的乘积形式。以此为基础，定义图像I′1、I′2分别为I1、I2的尺度规范化图像，其中I′1计算表达式为

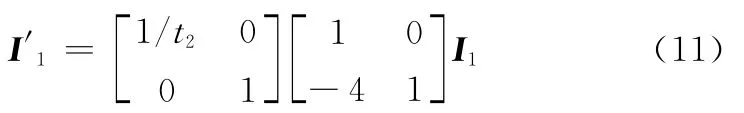
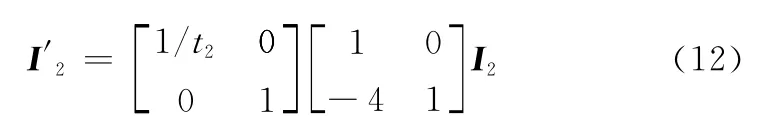
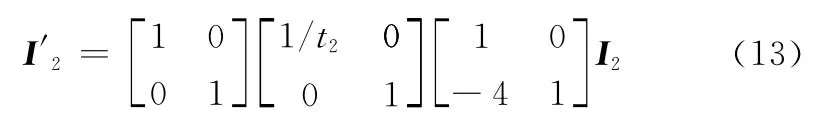
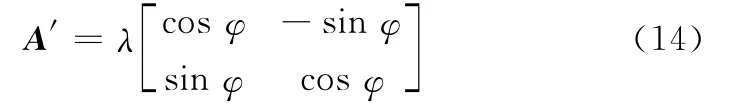
显然，由式（14）可知，图像I′1与I′2之间只包含有图像旋转变化φ与各向同性尺度变化λ（矩阵A′的奇异值：λ1＝λ2＝λ），因而此时直接采用SIFT算子即可获得足够多的匹配特征点进行图像配准处理。

综合上述分析可知，在全仿射形变条件下，为了克服各向异性尺度变化给图像配准带来的不利影响，可首先对未知参数t1、t2进行搜索估计，而后利用式（11）～式（13）对I1与I2进行尺度规范化处理，最后再利用SIFT算子提取匹配特征点进行图像配准处理。

2 未知参数t1、t2的估计

2．1 t1、t2的取值范围分析

由式（6）、式（7）、式（9）、式（10）可知，在不对矩阵A作近似处理的条件下，t1、t2的取值范围为无穷大，这对后续的参数搜索估计十分不利。为此，本文引入如下近似假设：令ai、aj为矩阵A中任意两个相邻的元素，假设｜ai／aj｜＞60，则矩阵A中元素aj可近似等于0。

为说明上述近似的有效性，首先令ai＝a1、aj＝a2且A的近似矩阵为，则A可表示为

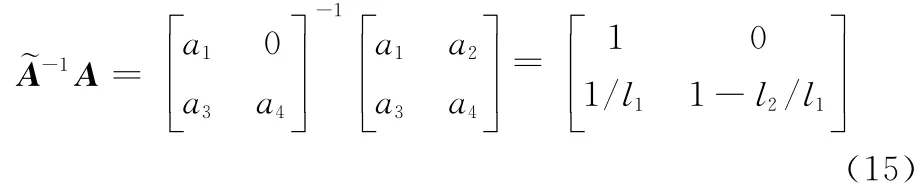
式中，l1＝a1／a2，l2＝a3／a4。将l1、l2代入式（2）、式（3），并由λ1／λ2≤20整理可得

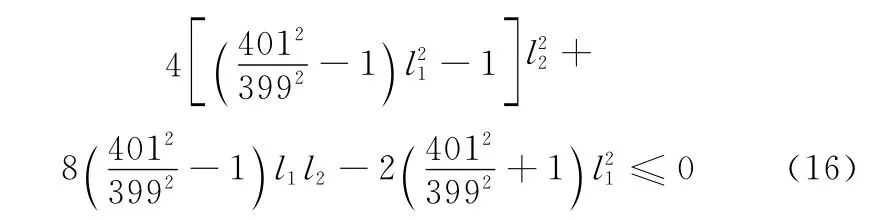
将｜l1｜＞60代入式（16）求解可得｜l2｜＜11．65。与式（16）类似，同理可证明：当｜a1／a3｜＞60时，｜a2／a4｜＜11．65；当｜a3／a1｜＞60时，｜a4／a2｜＜11．65；当｜a3／a4｜＞60时，｜a1／a2｜＜11．65。

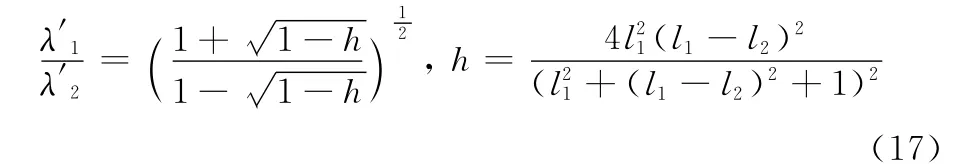
与a1、a2类似，对于矩阵A中其他任意两个相邻的元素ai、aj，可以证明：如果｜ai／aj｜＞60，则必然有˜A－1A的奇异值之比λ′1／λ′2＜1．24，亦即由矩阵˜A近似替代矩阵A引入的最大各向异性尺度变化小于1．24，对后续处理的影响可忽略不计，因而采用此种近似假设是合理可行的。

以上述近似假设为基础，参数t1、t2在不同情况下的取值范围分别如下：

且a2＝0时，由可知11．65。此时如果，则由式（6b）、式（7b）可知t∈1（－28．24，28．24）、t2∈（－1．46，1．46）；反之如果60，则由前述分析可知a3可近似为0，与之相对应，由式（9d）、式（10d）可得t1、t2的取值区间为［－1，1］。同理可得当且a4＝0时，如果，则t∈（－28．24，128．24）、t2∈（－1．26，1．26）；反之如果，则t1、t2∈［－1，1］。

综合情况（1）～情况（5）的分析结果可知，在对矩阵A进行合理近似的基础上，参数t1、t2的最大取值范围为t1∈（－33．51，28．24）、t2∈（－28．24，33．51）。

2．2 基于粒子群优化算法的t1、t2估计

粒子群优化（particle swarm optimization，PSO）算法是一种源于鸟群捕食行为研究的仿生迭代搜索算法，由于计算简单、易于操作而广泛应用于工程实践［14］。算法首先在问题空间构建一个粒子群，粒子群中每个粒子的空间位置代表待求解问题的一个可能解，而后通过对鸟群捕食行为的模拟，对每个粒子的空间位置进行迭代更新，以快速搜索得到待求解问题的最优解。

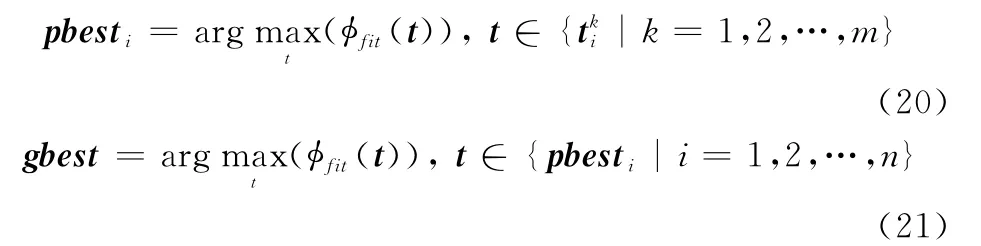
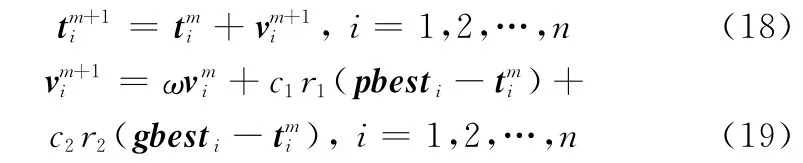
式中，n为粒子群中包含的粒子数；ω为随迭代次数增加线性递减的惯性权重；c1、c2为非负学习因子（通常取为2）；r1、r2为［0，1］间的随机数；pbesti表示粒子i当前已搜索到的最优位置向量；gbest为粒子群当前已搜索到的最优位置向量；φfit（·）为粒子适应度函数，用于评判粒子位置向量的优劣（即解的优劣），φfit（·）的具体定义由待求解问题的目标函数确定。本文中采用PSO算法的目的在于根据粒子的位置向量获取t1、t2的估计值，而后将其代入式（11）～式（13）得到的尺度归一化图像I′1与I′2，当粒子的位置向量与（t1，t2）的真实值相等时，I′1与I′2间不包含各向异性尺度变化，采用SIFT算子可以提取到大量的匹配特征点，而当粒子的位置向量与（t1，t2）的真实值不相等时，I′1与I′2间包含各向异性尺度，采用SIFT算子提取到的匹配特征点将会减少，因此在本文中将φfit（·）定义为I′1与I′2中提取到的SIFT匹配特征点个数。需要注意的是，由于实际中a1，a2，…，a4的值是未知的，因此对于粒子的每个位置向量，由式（12）和式（13）可同时得到两个图像I′2，将其分别与图像I′1组合并采用SIFT算子提取匹配特征点，假设提取的匹配特征点个数分别为N1、N2，则φfit（·）的最终取值为max（N1，N2）。以此为基础，采用PSO算法对t1、t2进行估计的具体过程如下：

步骤3 以pbesti的初始值为基础，根据式（21）计算gbest的初始值；

步骤4 根据式（18）、式（19）更新当前粒子的位置和速度向量；

步骤5 根据式（20）、式（21）更新pbesti与gbest的值，并记迭代次数m＝m＋1；

步骤6 判断m是否达到最大迭代次数，若达到则停止迭代，并将gbest值作为（t1，t2）的估计结果输出，否则转步骤5（由于待估计参数只有2维，取值空间较小，经过较少的迭代即可得到估计结果，因而此处将最大迭代次数设置为40）。

需要指出的是，文中在进行参数估计之前，首先对图像I1与I2进行了4×4的降采样处理，而后再根据降采样图像对（t1，t2）进行估计，以降低PSO算法的运算量，最后再依据估计结果对I1与I2进行尺度规范化与SIFT图像配准处理，以获取最终的图像配准结果。

3 实验分析

为了验证本文方法的有效性，本文以三组SAR图像数据为基础，对本文算法、SIFT算法以及ASIFT算法的性能进行实验比较。三组实验数据的待配准图像与参考图像分别由分辨率不同的两个机载SAR系统获得：第一组实验数据中，两个SAR系统成像时的航向角与下视角差异都较小，与之相对应，待配准图像与参考图像间的尺度变化是近似各向同性的；第二组实验数据中，两个SAR系统成像时的航向角差异较小，而下视角相差较大，与之相对应，待配准图像与参考图像间的尺度变化是各向同性的；第三组实验数据中，两个SAR系统成像时的航向角与下视角差异都比较大，其中航向角差异大于90，此时待配准图像与参考图像间的尺度变化不仅是各向异性的，而且仿射形变矩阵的行列式也是负的。

实验过程中，为避免错误匹配特征点的干扰，3种算法均采用了随机抽样一致法［15］对错误匹配特征点进行了剔除处理。实验所用计算机为酷睿i3（3．0G）、编程语言为Matlab7．6。

图1所示为第一组数据的实验结果，图像大小为500像素×600像素。由于此时待配准图像与参考图像间的尺度变化是近似各向同性的，因而直接采用SIFT算子即可提取到足够多的匹配特征点进行配准处理，其他两种方法提取到的匹配特征点亦与SIFT算子相当。

图1 第一组图像数据实验结果

图2所示为第二组数据的实验结果，图像大小为300像素×360像素。由于该组数据中待配准图像与参考图像间存在明显的各向异性尺度变化，因而此时SIFT算子失效，未能提取到匹配特征点，而本文算法与ASFIT法都提取到一定数量的匹配特征点，且ASFIT法由于受光轴角度采样误差的影响，提取到匹配特征点个数少于本文算法。

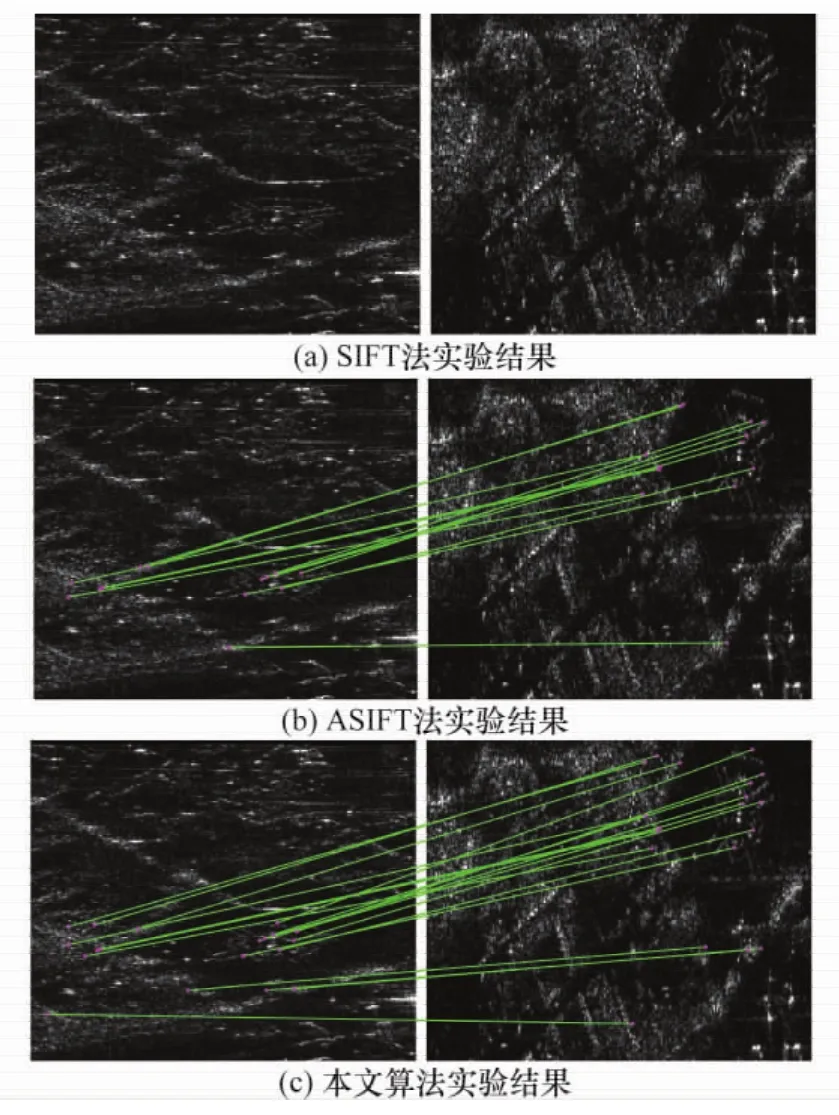
图2 第二组图像数据实验结果

图3所示为第三组数据的实验结果，图像大小为350像素×550像素。注意到对于该组数据，ASIFT法的实验结果与SIFT法的实验结果一样，都未能成功提取到匹配特征点。这是因为该组数据中待配准图像与参考图像间不仅存在各向异性尺度变化，而且两者之间对应的仿射形变矩阵的行列式为负。而ASFIT法由于限定仿射形变矩阵的行列式为正，与实际情况不符，因此所得实验结果与SIFT算子一样失效。而由图3（b）可知，对于本文方法，此时算法依然能够提取到一定数量的匹配特征点。

图3 第三组图像数据实验结果

表1所示为实验结果的参数对比，由表可知，对于三组实验数据，本文算法提取到的匹配特征点数分别为25、19、23，可以完成三组数据的配准处理，而ASFIT法仅能完成第一、第二组图像数据的配准处理，SFIT法则仅能完成第一组图像数据的配准。但由表亦可知，本文算法所需时间明显大于SFIT法，且亦大于ASFIT法，主要原因在于算法实现过程中需要采用PSO算法对t1、t2进行估计，增加了算法的运算量。

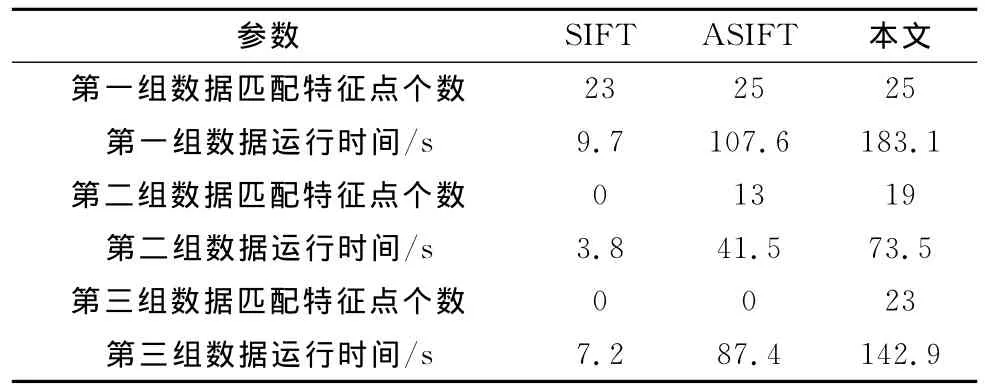
表1 实验结果参数对比

4 结 论

针对全仿射形变SAR图像配准中，待配准图像与参考图像之间存在各向异性尺度变化，导致匹配特征点提取困难的特点，本文提出了一种基于仿射形变矩阵分解与尺度变化矩阵估计的点特征图像配准算法。该方法首先将仿射形变矩阵分解为图像旋转矩阵、尺度变化矩阵以及常数矩阵的乘积，而后对尺度变化矩阵中的未知参数进行估计，并利用估计结果对待配准图像与参考图像进行尺度规范化处理，最后再利用SIFT算子提取匹配特征点，进行图像配准。SAR图像数据验证表明，通过尺度规范处理，本文方法可以有效抑制各向异性尺度变化带来的不利影响，增加SIFT算子提取到的匹配特征点数量，从而实现全仿射形变条件下的SAR图像配准。同时实验结果亦表明，本文算法由于需要对尺度变化矩阵中的未知参数进行估计，增加了算法的运算量，降低了算法运行速度。为此，在后续工作中，将就参数估计方法的优化改进作进一步研究。

［1］Bruzzone L，Bovolo F．A context－sensitive technique robust to registration noise for change detection in VHR multispectral images［J］．IEEE Trans．on Image Processing，2010，19（7）：1877－1889．

［2］Song X L，Wang Q．Joint image registration and super－resolution reconstruction based on regularized total least norm［C］∥Proc．of the 16th IEEE International Conference on Image Processing，2009：1537－1540．

［3］Das A，Revathy K．Image fusion techniques for remote sensed SPOT images［C］∥Proc．of the International Conference on Computational Intelligence and Multimedia Applications，2007：482－489．

［4］Zitova B，Flusser J．Image registration method：a survey［J］．Image and Vision Computing，2003，21（11）：977－1000．

［5］Yi C L，Wang Z M，Guo L Y．Automatic sub－pixel registration for SAR image based on control point［J］．Computer Simulation，2010，27（8）：243－246．（易成龙，王正明，郭良益．基于控制点的SAR图像亚像素自动配准［J］．计算机仿真，2010，27（8）：243－246．）

［6］Wu Y D，Zhang X，Yang M．Automatic and reliable registration for SAR complex image［C］∥Proc．of the Multispectral Image Acquisition and Processing，2009：1－7．

［7］Lin X H，Zhang Y Z，Yang Y J．Application of triangulationbased image registration method in the remote sensing image fusion［C］∥Proc．of the International Conference on Environmental Science and Information Application Technology，2009：501－504．

［8］Lowe D G．Distinctive image features from scale－invariant key points［J］．The International Journal of Computer Vision，2004，60（2）：91－110．

［9］Yan K，Sukthankar R．PCA－SIFT：a more distinctive representation for local image descriptors［C］∥Proc．of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2004：506－513．

［10］Bay H，Tuyteplaars T，Van G L．Surf：speeded up robust feature［C］∥Proc．of the European Conference on Computer Vision，2006：404－417．

［11］Wang G X，Huang X T，Zhou Z M．SAR image scale invariant feature extraction algorithm［J］．Journal of Image and Graphic，2011，16（12）：2199－2205．（王广学，黄晓涛，周智敏．SAR图像尺度不变特征提取方法研究［J］．中国图象图形学报，2011，16（12）：2199－2205．）

［12］More J M，Yu G S．ASIFT：a new framework for fully affine invariant image comparison［J］．SIAM Journal on ImagingScience，2009，2（2）：438－469．

［13］Yang Q．Matrix analysis［M］．Beijing：China Machine Press，2005．（杨奇．矩阵分析［M］．北京：机械工业出版社，2005．）

［14］Kennedy J，Eberhart R C．Particle swarm optimization［C］∥Proc．of the IEEE International Conference on Neural Networks，1995：1942－1948．

［15］Zhou J，Chen L T，Liu Q H，et al．Fast and accurate ransac based on optimal sequential probability test and local optimization［J］．Chinese Journal of Scientific Instrument，2012，33（9）：2037－2044．（周骏，陈雷霆，刘启和，等．基于序贯概率及局部优化随机抽样一致性算法［J］．仪器仪表学报，2012，33（9）：2037－2044．）

E－mail：13366629518＠189．cn

王广学（1981－），男，讲师，博士，主要研究方向为SAR图像处理。

E－mail：wgxradar＠163．com

栗 苹（1966－），女，教授，博士研究生导师，博士，主要研究方向为目标探测和信息对抗。

E－mail：lipin85＠bit．edu．cn

闫晓鹏（1976－），男，教授，博士研究生导师，博士，主要研究方向为近感探测和信息对抗。

E－mail：yanxiaopeng＠bit．edu．cn

Fully affine SAR image registration method based on feature points

LIU Yong－chun1，WANG Guang－xue2，LI Ping1，YAN Xiao－peng1
（1．National Key Laboratory of Mechatronic Engineering and Control，Beijing Institute of Technology，Beijing 100081，China；2．Department of Information Countermeasure，Air Force Early Warning Academy，Wuhan 430019，China）

In the fully affine synthetic aperture radar（SAR）image registration conditions，the scale change between reference images and registering images is non－isotropy，which makes it difficult to extract enough matching feature points for the traditional image registration method based on feature points．To deal with this problem，a new image registration algorithm based on feature points is proposed．The affine matrix is first decomposed into products of image rotation matrixes，scale change matrixes，and constant matrixes．Then the unknown parameters in scale change matrixes are estimated by the particle swarm optimization（PSO）method．Based on the estimation result，reference and registering images are normalized to suppress the non－isotropy scale change between them．After that，the scale invariant feature transform（SIFT）operator is employed to extract matching feature points，and the image registration is based on it．The experimental results show that，for the fully affine SAR image registration，the proposed algorithm can obtain more matching feature points than the existed methods，so it has a better performance．

synthetic aperture radar（SAR）image registration；affine transform；particle swarm optimization（PSO）algorithm；scale invariant feature transform（SIFT）operator

TP 391．41

A

10．3969／j．issn．1001－506X．2015．06．06

刘永春（1976－），男，博士研究生，主要研究方向为智能探测与控制。

1001－506X（2015）06－1259－07

2014－05－23；

2014－10－20；网络优先出版日期：2014－12－08。

网络优先出版地址：http：／／www．cnki．net／kcms／detail／11．2422．TN．20141208．1057．005．html

国家自然科学基金（61302194）资助课题