基于状态记忆的航天器自主故障诊断方法
2015-08-17王日新徐敏强
金 洋,王日新,徐敏强
(1.中国民航大学航空工程学院,天津300300;
2.哈尔滨工业大学深空探测基础研究中心,黑龙江哈尔滨150080)
基于状态记忆的航天器自主故障诊断方法
金 洋1,王日新2,徐敏强2
(1.中国民航大学航空工程学院,天津300300;
2.哈尔滨工业大学深空探测基础研究中心,黑龙江哈尔滨150080)
针对基于传统第一原理理论的诊断方法中,由于忽略了自主诊断时历史诊断结果对当前诊断的影响而导致无谓消耗大量计算量的问题,提出了新的诊断方法。通过在传统的方法中引入状态记忆机制,扩展了诊断与冲突的含义。根据诊断解的结构分析了基于第一原理诊断方法中诊断解的分布,并利用分析结果证明了新的诊断方法在效率上优于传统的诊断方法。通过引入“时间戳”和“状态锁”,使得诊断方法能够自主地处理遥测数据在不同输入方式下的诊断问题。
故障诊断;第一原理;状态记忆;诊断效率
0 引 言
目前航天器自主故障诊断技术已经成为保障系统在轨期间安全可靠运行的重要手段之一。航天器是一种复杂度高、投入高、风险高的系统,故障发生时若没有及时发现和处理,其后果可能是灾难性的[1-3],因此在航天器发生异常时就需要故障诊断系统能够迅速地识别出系统当前的状态,从而为航天器控制与管理系统提供决策依据,这就要求诊断方法具有较高的执行效率,从而保证航天器自主故障诊断系统具有较好的实时性。
NASA在航天器自主故障诊断技术方面进行了深入的研究[4-6]。其中由Ames中心开发的Livingstone系统是一种基于定性模型的诊断系统,采用命题表达式的方式描述系统的功能,并基于第一原理理论开发诊断引擎。该系统也被成功地应用到EO-1[7]以及其他自主系统中[8]。
基于定性模型的故障诊断方法能够利用系统的结构、功能及因果关系等知识建立系统模型[9-10],既克服了历史数据中可能无法包含系统运行全部特征的问题,又克服了专家经验不易提取的问题,同时也不需要建立精确的数学模型,已成为故障诊断方法的主要研究方向之一。
在国外,Reiter[11]最初建立了基于第一原理的定性模型诊断方法的理论基础,并提出了基于“冲突识别”和“候选产生”的诊断框架。Williams[12]基于传统的第一原理诊断理论提出了CBFS算法,该算法使用传递系统模型[13]对具有多故障模式的系统进行建模。由于诊断过程是通过遍历所有的传播路径进行冲突识别的,因此计算量非常大。Kurien[14]在此基础上提出了Cover-Track算法,降低了枚举规模,该算法在后续的研究中也得到了应用[15]。但是整个算法的在线计算量依然很大。
在国内,学者们分别从冲突识别和候选产生两方面进行了研究。其中文献[16-17]提出了CSSE-tree以及CSISE-tree来产生最小冲突集,并提出了基于冲突的离散系统诊断方法。此外,文献[18]提出了用对分HS-树计算最小hitting集的方法,文献[19]利用遗传算法控制hitting集的计算规模,能够很好地提高算法的计算效率,文献[20]还提出了MUOUE算法计算最小hitting集并将其应用到基因检测中。
本文作者在前期对基于第一原理诊断方法进行了深入的研究,分别从诊断策略、模型结构以及诊断过程中的不确定性问题出发提出了相应的算法[9,21-22],缩减了实时计算规模,有效地提高了实时诊断效率。
但是上述方法没有考虑自主过程中存在的连续诊断优化问题,都是从一次诊断过程中的操作效率出发进行研究,从而忽略了历史诊断结果对本次诊断的影响,使得每次诊断都是独立的,导致当系统的状态相对于初始状态发生改变后,每一次诊断都需要根据初始状态重复进行候选产生操作,无谓消耗了大量的计算量。
本文从连续多次诊断过程出发来研究诊断效率的优化问题,在基于传统的第一原理诊断理论的方法中引入状态记忆机制,将诊断的历史结果引入到以后的诊断过程中,提出新的诊断方法,避免无效诊断,消除无谓的计算量,提高诊断算法的效率,以满足航天器故障诊断系统的实时性需求。同时,从理论上对诊断解的结构进行分析,为诊断结果的评价提供依据。
1 基于状态记忆的诊断原理
在Reiter的理论中,诊断的基础在于如何看待“诊断”与“冲突”,并在文献[11]中给出了形式化的定义。在定义中,“诊断”被描述为一个集合,其特点是集合中的每一个部件都是故障的,而集合外的其他部件都是正常的。同时,“冲突”被描述为这样一个集合,其特点是如果集合中的所有部件都是正常的,那么这将与系统的观测是不一致的。
在这些定义中,诊断的目的是寻找故障,这相当于在诊断过程中引入了每一个状态的物理意义,而不考虑历史的诊断结果与当前诊断的关系,诊断过程可概括为以下3种情况:
(1)t-1时刻系统被诊断为无故障,并且t时刻不存在理论值与观测冲突的部件,这时的诊断只包括冲突识别过程。
(2)t-1时刻系统被诊断为无故障,并且t时刻存在理论值与观测冲突的部件,这时诊断包括两部分内容:冲突识别与候选产生。如果模型中包含多个故障模式,则还要确认部件的故障模式。
(3)t-1时刻系统被诊断为有故障,并且t时刻存在理论值与观测冲突的部件,这时诊断包括两部分内容:冲突识别与候选产生。同样地,如果模型中包含多个故障模式,则还要确认部件的故障模式。
通过以上分析,对于情况(3),在t-1时刻系统被诊断为有故障时,仍然将系统的初始状态设定为正常状态进行冲突识别操作的流程显然是不合理,并且如果部件发生的故障不能及时得到消除,即部件的状态将保持上一时刻的故障状态,则进行的候选产生操作仍然会被重复执行,从而消耗无谓的计算量。
本文为了解决这个问题,提出了能使诊断具有状态记忆能力的机制,并对“诊断”和“冲突”的定义给予新的描述。
定义1 (SD,COMPONENTS,OBSt2)在t2时刻的一个诊断是一个最小集合Δ⊆COMPONENTS,该集合使得是相容的。
其中,G(c,s1,s2,t1,t2)等价于:CON(s1,s2)∧L(c,s1)∧T(s1,t1)∧L(c,s2)∧T(s2,t2)为真,t1<t2;SD是对系统结构的描述;COMPONENTS是所有部件组成的集合;OBSt1代表t1时对系统状态的观测集合;CON(s1,s2)代表s1与s2是两个一致的状态;L(c,s1)代表部件c当前处于的状态s1;T(s1,t1)代表t1时刻系统的状态为s1。所以,这里的表达式G(c,s1,s2,t1,t2)描述了部件c在t1时刻的状态s1(即L(c,s1)∧T(s1,t1))与在t2时刻的状态s2(即L(c,s2)∧T(s2,t2))是一致的。
在定义1中,诊断结果已经不再代表系统的故障部件集合,而代表的是在t-1和t两个时刻状态发生改变的集合。而Reiter的理论中描述的诊断结果可视为定义1在考虑状态的物理意义情况下的特例,即Reiter的理论中,t1时刻的状态始终与初始时刻的状态相对应。
若假设t1和t2是相邻的,那么基于定义1的诊断过程相当于对上次的诊断过程具有记忆性。
下面给出与定义1相对应的冲突集的形式化描述。
定义2 (SD,COMPONENTS,OBSt1)在t1时刻的一个冲突集是一个最小集合{c1,c2,…,ck}⊆COMPONENTS,该集合使得
SD∪OBS∪{G(c1,s1,s2,t1,t2),…,G(ck,s1,s2,t1,t2)}不相容。
定义2表明,如果t1与t2是相邻的,则冲突识别的结果将是与t1时刻的系统状态不一致的t2时刻的状态,而不代表异常的部件集合。
2 基于状态记忆的诊断方法
由于基于模型的诊断方法是通过将模型的推理值与观测值进行一致性检验来实现异常检测,进而实现故障定位的,因此观测数据的质量对诊断的结果、诊断的效率以及诊断的流程起到重要的作用。
通过将在引言中提到的传统的基于模型诊断原理与本文在定义1中所描述的基于状态记忆的诊断原理进行比较可以看出,利用后者在进行两次连续的诊断时,前一时刻的诊断结果将作为当前时刻的初始状态。因此,在这种情况下,前一时刻的诊断结果是否完整将决定当前诊断操作的执行顺序。而诊断结果的完整性则取决于诊断时观测数据的完整性。
在使用连续诊断策略对航天器进行诊断时,遥测数据的完整性则成为影响诊断过程的重要因素。考虑到航天器的系统组成复杂,遥测参数数量众多、数据传输带宽有限、不同部件的遥测参数的采样频率不相同等因素[23],使得某一时刻能够完整描述系统状态的观测将在多个时刻被采集到。此时,如果以状态的采样时间作为时间戳,则这些数据帧的时间戳相同,而数据的传输时间不同,即每次诊断将无法得到系统的完整状态,影响了诊断结果的完整性并可能扰乱诊断流程的进行。
因此,在利用基于状态记忆机制进行自主诊断时,就要求诊断算法能够自主地处理这种观测不完整情况下的诊断问题。
根据诊断数据时间戳的一致性,即观测数据的完整性,诊断过程的输入可分为以下两种情况。
(1)利用不同时间戳的观测进行诊断
具有不同时间戳的观测数据描述的是系统在不同时刻的状态,系统在这两个时刻的状态可能是不同的,所以其诊断过程与文献[17]中的方法类似,只是此时诊断解描述的是与上一时刻相比,状态发生变化的部件。
(2)利用相同时间戳的观测进行诊断
时间戳相同的观测数据在物理意义上描述的是同一时刻的系统状态。当系统在某时刻的完整状态数据通过多帧下传时,等待能够完整描述系统状态的数据可能会延误诊断操作。为了解决这个问题,本文在诊断方法中引入了“先来先诊断”的策略,即将系统的完整状态在多次诊断过程中逐渐完成。
这种策略的优点是:①时效性好,诊断及时;②对观测的依赖小,能够适应数据传输的限制问题。
在利用不同时间戳的观测进行诊断时,利用后一帧数据的诊断是以利用前一帧数据得到的诊断结果为基础的,与情况(1)不同,此时某些部件的工作状态已经被确定下来,在当前诊断过程中不可改变,也只有这样才能够正确地描述该时间戳对应的系统状态。
基于上面的分析,本文对利用基于状态记忆机制的诊断方法在处理观测数据不完整情况下各部件的状态进行约束。
(1)当两次诊断利用的观测时间戳相同时,利用上一帧数据得到的系统局部状态在此次诊断时是不可变的,因此当前诊断时需要对系统的这些局部状态进行“锁定”;
(2)当两次诊断利用的观测时间戳不同时,表明系统的状态在两次诊断之间是可变的,因此当前诊断时需要对系统的状态解锁,并在本次诊断时重新确定;
(3)根据(1)和(2),只有当观测数据的时间戳不同时,系统的时间戳才可以被更新。
在连续诊断策略中,“时间戳”与“状态锁”机制的引入将两种不同的诊断情况进行了统一。图1描述了基于这种机制统一起来的诊断闭合回路。
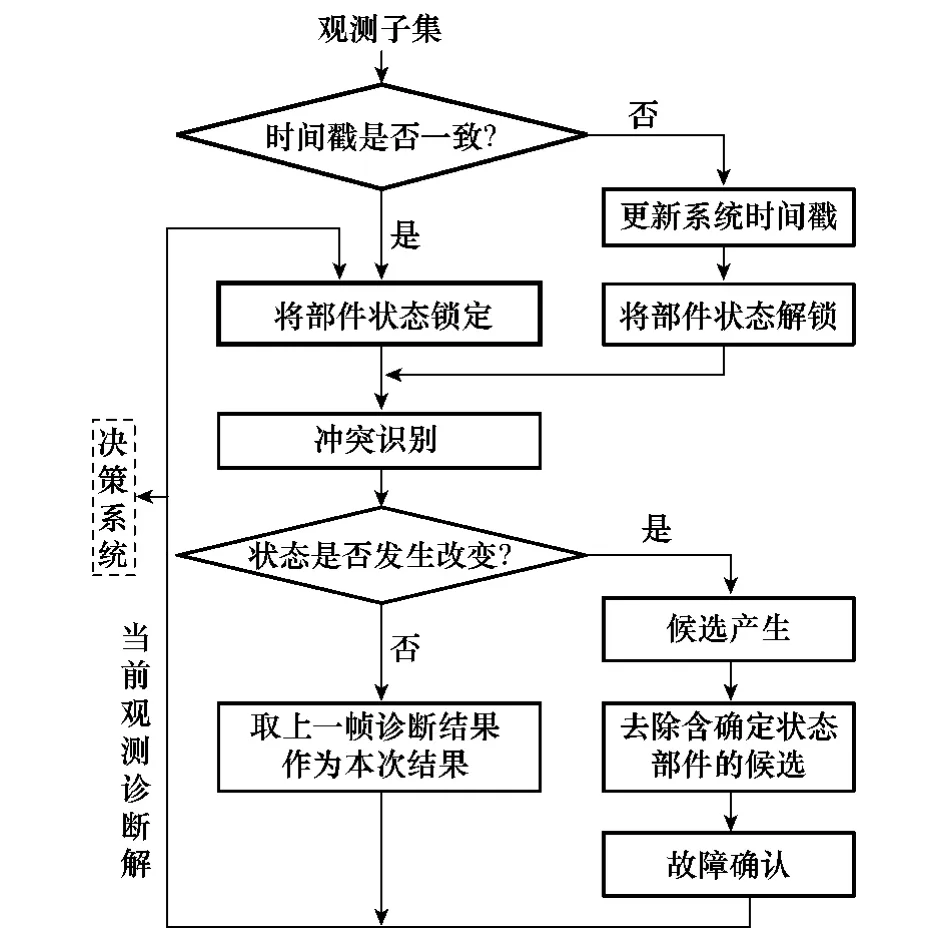
图1 基于状态记忆的诊断流程图
同时,由于引入了“时间戳”与“状态锁”,本文提出的基于状态记忆机制的诊断方法能够针对不同的观测输入情况进行正确的诊断,在保证诊断结果准确性的同时,也提高了诊断方法的自主处理能力。
3 对诊断解结构的分析
本节对基于第一原理的诊断方法的诊断结果进行了分析,得到了描述诊断解分布情况的相关结论,以这些结论为理论依据可以有效地对诊断过程进行评价。
在根据Reiter提出的传统诊断理论进行诊断时,首先需要进行冲突识别操作,然后根据获得的冲突集计算最小碰集,最终得到故障部件集合。图2为Reiter给出的简单电路系统,其中A1、A2为加法器,M1、M2、M3为乘法器。根据图2中描述的系统结构以及观测数据,冲突集为{M1,M2,A1}和{M1,M3,A1,A2},诊断解为{{M1},{A1},{M2,M3},{A2,M2}}。
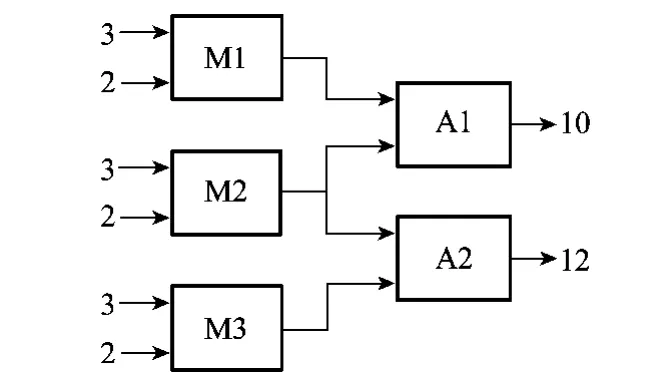
图2 电路系统结构图
在引入冲突候选集的概念后,冲突识别的结果包括两部分内容:①观测与理论值冲突的候选集,即冲突集;②观测与理论值一致的候选集。由于在以往的研究中,那些不存在冲突的候选集在冲突识别后不在参与后面的计算而被忽略了,但是在这些集合中仍然隐含了与诊断解的结构与分布情况有关的信息。
通过对图2所示系统的结构进行分析,得到冲突候选集为{M1,M2,A1}、{M2,M3,A2}和{M1,M3,A1,A2}。此时诊断解{M2,M3}与{A2,M2}只在理论上具有可能性。在某些系统中,仅仅利用冲突集得到的诊断解有时是与系统的物理意义不符合的。下面以图3中的实例进行说明,该实例由NASA开发的Livingstone系统给出。图中可观测的参数为电池battery的电量状态、收音机radio以及钟表clock的工作状态。根据系统的结构与测点位置得到冲突候选集为{battery,fuse,radio},{battery,fuse,clock}以及{radio,clock}。设置系统当前的工作场景为:打开开关后radio没有输出,而clock工作状态正常。根据传统的方法得到的结果,诊断解为{radio},{battery,clock}以及{fuse,clock}。显然{battery,clock}、{fuse,clock}都是候选集{battery,fuse,clock}的子集,并且该候选集的推理值与观测值是一致的。然而,根据clock的物理意义,诊断解{battery,clock}与{fuse,clock}是不合理的。
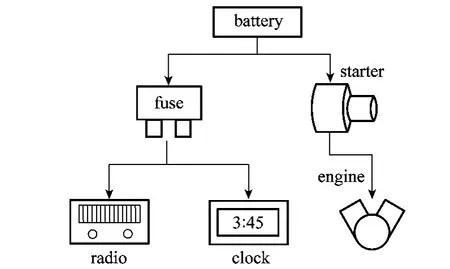
图3 示例系统模型结构
上述分析表明,诊断解的信息是同时包含在冲突集与非冲突集中的。
通过对诊断解与冲突候选集进行分析,可以得到以下结论。在这些结论中,单诊断解代表的是诊断解集合中只有一个元素,而多诊断解代表的是诊断解集合中的元素数多于一个。
定理1 非冲突的候选集中不包含单诊断解。
证明 设{C1,C2,…,Ck}是一个非冲突候选集,其中C1为系统的一个诊断解。由定义1可知C1在t1和t2时刻的状态是不相同的。再由定义2,可推得候选集{C1,C2,…,Ck}是一个冲突集。然而,这与{C1,C2,…,Ck}是一个非冲突候选集的假设矛盾。
证毕
定理2 单诊断解属于所有冲突集的交集。
证明 设C1是系统的一个单诊断解。由诊断的含义可知,C1故障模式的推理值与系统当前的观测一致。由冲突的含义可知,C1可以对所有冲突集的冲突原因进行解释。设C2可以对不包含C1的冲突集{C2,C3,…,Ck}的冲突原因进行解释,则由定义2,{C1,C2}是一个多诊断解。这与C1是单诊断解的假设矛盾。
证毕
定理3 如果一个系统是连通的,则任何一个冲突集中不包含多诊断解。
证明 设冲突集{C1,C2,…,Ck}及诊断解C1∈{C1,C2,…,Ck}。设{C1,C2}⊂{C1,C2,…,Ck}是一个多诊断解,则{C1,C2}是一个最小解集合,{C1}和{C2}不是诊断解。这与前面的假设矛盾。
证毕
定理4 如果一个系统是连通的,则多诊断解一定包含在非冲突候选集中。
下面首先证明3个引理,并依据这些引理对定理4进行证明。
引理1 如果Ai是一个连通系统的冲突候选集,则一定存在候选集Aj使得Ai∩Aj≠φ成立。
证明 设冲突候选集{C1,C2,…,Ck}与其他候选集均不相交,则以C1为输入的通路只有一个输出Ck,即{C1,C2,…,Ck}所描述的子图与其他子图不连通。这与系统连通的假设矛盾。
证毕。
引理2 一个连通系统的所有冲突集的并与所有冲突候选集的并相等。
证明 设冲突集S1={C1,…,Ai,…,Ck}与非冲突集S2={D1,…,Aj,…,Dp}相交,A为公共节点(S1中第i个节点,S2中第j个节点),则必存在两个冲突集S3={D1,…,Dj-2,Dj-1,Ai,Ci+1,…,Ck}与S4={Ck,Ck-1,…,Ci+1,Dj+1,…,Dp-1,Dp}的推理值与观测不一致,即冲突集覆盖了所有的节点。
同理,若有其他的非冲突集与S1或S3或S4相交,那么将会产生新的冲突集,并且非冲突集将是这些冲突集的子集。
证毕
引理3 连通系统的所有非冲突集的并与那些只属于部分冲突集的节点的并相等。
证明 由定理2、定理3可知,所有属于各冲突集交集的部件都是一个单诊断解。设部件C既属于各冲突集的交又属于某非冲突集,那么{C}是系统的一个单诊断解,这说明它既能够解释所有冲突集的产生原因,也能够解释该非候选集没有冲突的原因,而这与定义1矛盾,即各冲突集的交和非冲突集的交是空集。由引理2可知,各非冲突集的并是各冲突集的并集的子集,所以各非冲突集的并集将等于各冲突集的并集与各冲突集的交集之差。证毕
下面对定理4进行证明。
证明 由定理3、引理3可知,多诊断解一定属于非冲突集的并。并且由定理1,可得多诊断解一定属于非冲突集。
证毕
下面本文给出强、弱诊断解集的概念。
定义3 强诊断解集是由各单诊断解构成的集合。
定义4 弱诊断解集是由所有诊断解(单诊断解与多诊断解)构成的集合。
定义3、定义4说明,强诊断解集包含于弱诊断解集,前者代表了最可能发生的诊断解,而后者则描述了在逻辑上的所有可能解。
4 诊断算法分析
4.1 利用相同时间戳的观测进行诊断时的诊断解一致性
定理5 利用相同时间戳的观测进行诊断时,诊断结果与输入观测的顺序无关。
证明 设在利用相同时间戳的观测进行诊断时,若输入观测的顺序不同,得到的两个诊断解是不相同的。
由于诊断解是通过计算所有冲突集的最小碰集来获得的,而冲突集的获得是通过输入的观测数据对冲突候选集的评估得到的,因此上述假设等价于在这两种不同的输入顺序下,所产生的冲突集是不同的。
设一个冲突候选集C(C1,C2,…,Cn)在一种输入顺序下产生冲突,记为冲突集C’;在另一种输入顺序下不产生冲突,记为非冲突集C’。这里有C=C’=C’。
由于系统所有的观测值描述的是同一时刻的系统状态,因此输入值与输入的顺序无关。同理,对于C’和C’来说,其代表的数据传播路径的状态输入与状态输出应相同。但是这与C’和C’分别为冲突集和非冲突集的假设矛盾。因此,在利用“状态内的连续观测”进行诊断时,对于观测的两种不同输入顺序,所产生的冲突集是一致的,从而利用这些冲突集计算出的最小碰集是一致的,即诊断解是一致的。所以诊断结果与输入顺序无关。证毕
以图3系统为例,设各个部件的初始状态为:battery充满电,fuse打开,radio关闭,clock打开。
在t1时刻打开radio,根据radio的工作原理得到radio应该有输出,但是实际观测无输出,则经过冲突评估得到{battery,fuse,radio}是一个冲突集,并且通过计算hitting集得到诊断解为{battery}、{fuse}和{radio}。在t2时刻输入对clock的观测结果(输出正常),并判断{battery,fuse,clock}、{radio,clock}是否存在冲突。若诊断解为{battery}时,{battery,fuse,clock}存在冲突,表明此时无法对{clock}的状态进行合理的解释。由于{battery}、{fuse}处于锁定的状态,则t2时刻诊断解为{battery,clock}。同理,若{fuse}为诊断解时,则得t2时刻{fuse,clock}为诊断解,若诊断解为{radio}时,则{radio,clock}不存在冲突。因此,两次输入的诊断解集为{{battery,clock},{fuse,clock},{radio}}。
当观测数据以相反的顺序输入时,t1时刻对clock的观测结果正常,可推理出{battery}、{fuse}和{clock}正常,由定理4可以推出{battery,fuse,clock}包含一个多诊断解。在t2时刻对radio进行观测,推理得到候选集{battery,fuse,radio}存在冲突。若{battery}工作正常,则{fuse,clock}为一个诊断解。若{fuse}工作正常,则{battery,clock}为一个诊断解。对于候选集{radio,clock}来说,若{clock}工作正常,则{radio}为一个诊断解。因此,在这种观测的输入顺序下,系统的诊断解集同样为{{battery,clock},{fuse,clock},{radio}}。
4.2 诊断效率分析
在文献[17]中,分析了基于Reiter诊断理论提出的方法的计算规模。图4是文献[17]中给出的典型航天器一次电源系统结构图。其中包括太阳帆板SG,并联调节器S3R,误差放大器Vmea,母线BusBar,充电调节器BCR,放电调节器BDR,镍氢电池组BAT。传感器布点为图中节点A、B、C、D、E。
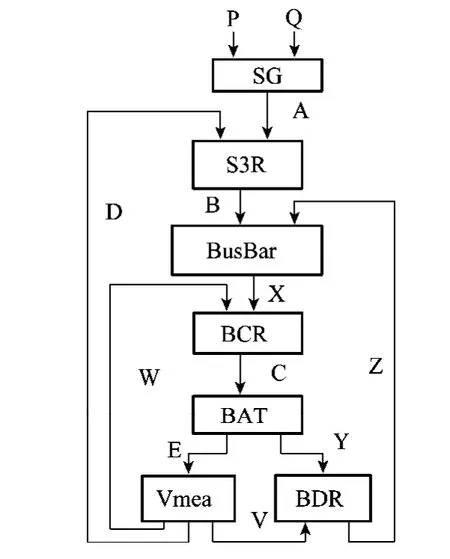
图4 一次电源系统结构模型
由模型的结构和传感器布置情况可以计算出模型的冲突候选集为:{BusBar,BCR,BAT,Vmea,BDR}、{SG}、{S3R}。
假设当前的系统观测状态为:测点B存在冲突,经计算得到系统的冲突集为{S3R}和{BusBar,BCR,BAT,Vmea,BDR}。通过计算hitting集得到系统的诊断解为{S3R,BusBar},{S3R,BCR},{S3R,BAT},{S3R,Vmea},{S3R,BDR}。
若只有测点B的值异常,则部件S3R的正常工作环境应为
表1为S3R设置的故障模式。根据部件的工作环境,S3R的工作状态为FM2。
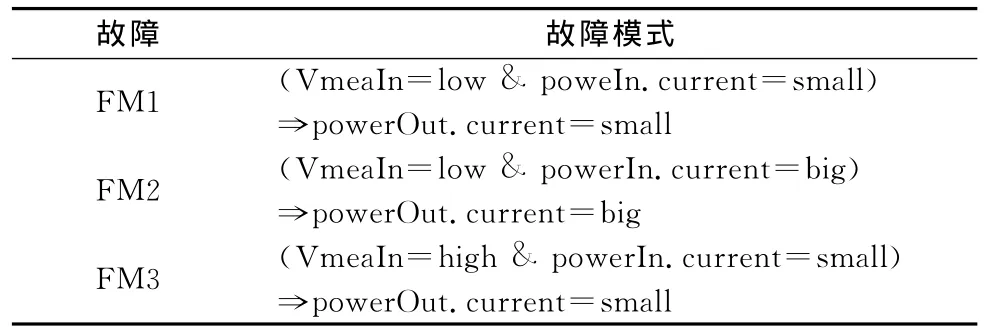
表1 S3R的典型故障模式
为了评价诊断方法的计算规模,将评价标准设定为参与诊断的工作模式的数量,则诊断过程中主要消耗的计算量为:
(1)冲突评估:u×v,u表示冲突候选集数量,v表示候选集中包含节点的平均个数;
(2)候选产生:p×q,p表示冲突集数量,q表示冲突集中包含节点的平均个数;
(3)状态确认:k×n×mn,k表示异常部件集合的数量,n表示异常部件集中包含节点的平均个数,m表示各节点中需要参与计算的模式的平均个数。
根据文献[17]中提出的诊断算法可得诊断过程中需要的故障模式为
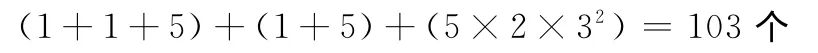
在本文提出的连续诊断策略中,无论是利用不同时间戳的观测进行诊断还是利用相同时间戳的观测进行诊断,可以看出图1所示的诊断流程与以往的类似,而时间戳的更新、状态的锁定与解锁等操作需要的计算量相对较小,可忽略。
在对本文所提诊断算法的效率进行评估时,将从以下两方面进行分析:
(1)状态在相邻两次诊断之间发生了变化
当系统状态发生改变时,主要计算量为利用不同时间戳的观测进行的诊断。对于一次诊断:若当前的观测数据可以完整描述当前的状态时,则此时的诊断过程与以往的相同,需要的计算量也与以往相同;若当前的观测数据无法完整描述当前的状态时,设需要计算的候选集为u′个、得到的冲突集为p′个、得到的异常部件集为k′个、每个集合内平均包含n′个节点,那么将出现以下3种情况。
①在观测能够描述局部状态时,需要计算的候选集数量少于观测体现全局系统状态时需要计算的候选集数量,即u′<u,由于有效观测少,因此可参与计算的候选集少。
②在观测能够描述局部状态时,得到的冲突集少于观测体现全局系统状态时的冲突集,即p′<p。
证明 假设增加一个观测a后引入的一个可识别的候选集为M,增加a之前所有的候选集的并为N,则M-M∩N≠Ø。若M是一个冲突集,则p′<p成立;若M是一个非冲突集,则根据引理3,M-M∩N中的部件至少属于一个新的冲突集,故p′<p成立。证毕
③输入的观测不完整时异常部件集合的个数和集合内平均的节点数小于输入的观测完整时异常部件集合的个数和集合内平均的节点数,即k′<k,n′<n。
证明 设增加一个观测a后得到了一个新的候选集为M,若没有增加a前得到的候选集的并集为N,则有M-M∩N≠Ø。若M为冲突集,由定理2、定理3,M-M∩N中将存在能够与N中的部件组成多诊断解的部件,因此k′<k、n′<n成立;若M为非冲突集,则由引理3,M-M∩N至少包含于一新的冲突集,故k′<k、n′<n。证毕
例如,对于一次观测,消耗计算量最大的观测子集为B、C、E,则在进行冲突评估时,只得到冲突集{BusBar,BCR,BAT,Vmea,BDR}。计算最小碰集可得到冲突候选集为{BusBar}、{BCR}、{BAT}、{Vmea}和{BDR}。
此时,通过计算可以得到当输入的观测不完整时参与计算的故障模式数为(5)+(5)+(5×1×32)=55个。
(2)状态在相邻两次诊断之间未发生变化
此时,无论是利用不同时间戳的观测进行诊断还是利用相同时间戳的观测进行诊断,由定义1、定义2,只需执行“冲突评估”操作。而由于以往的方法始终将系统初始的正常状态作为评估根据,所以在初始状态改变后每次都需重新执行完整的诊断操作。
利用本文的方法,由于在状态未发生改变时,进行冲突识别后不会产生表征状态改变的冲突集,因此不需要进行候选产生操作。所以需要的计算量为:(1+1+5)=7个。
表2是文献[17]提出的基于分离策略的算法的计算量、本文提出的基于连续诊断策略的算法在不同条件下所需计算量的对比。对比结果表明,本文提出的方法需要的计算量少于以往的方法。图5为引入状态记忆机制前、后消耗计算量的定性关系。

表2 算法所需计算量比较
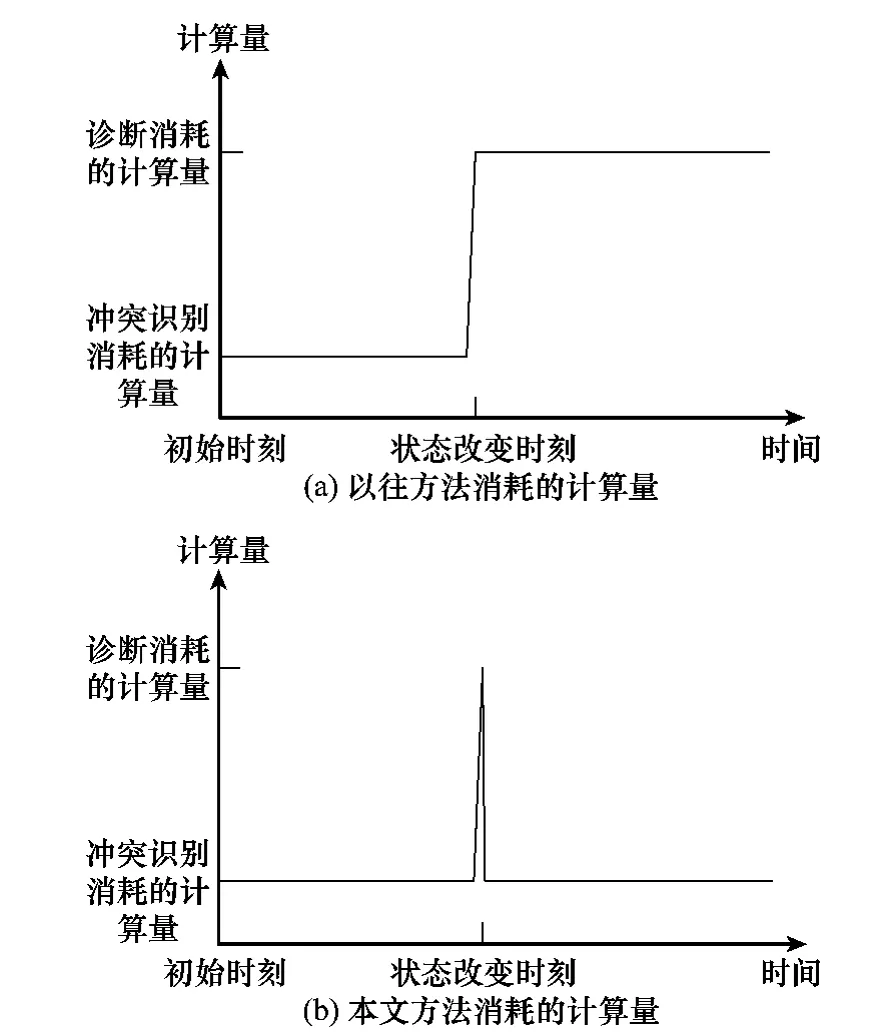
图5 两种方法所需计算量的定性关系
5 结 论
本文基于航天器自主管理系统对故障诊断过程实时性的要求,针对基于传统诊断理论的诊断方法无谓消耗计算量的问题,提出了新方法。
本文的关键之处在于:
(1)提出了状态记忆机制,扩展了传统的诊断与冲突的概念,通过引入多次诊断之间的影响关系,将历史的诊断结果作为当前系统的依据,减小了计算量;
(2)通过分析诊断解的结构,得到了诊断解的分布情况,为评价诊断过程提供了依据;
(3)将诊断方法应用到实际系统的诊断过程中,提出了能够适应不同观测输入顺序的诊断方法,有效地降低了诊断过程对测量条件的依赖,提高了诊断的时效性。
[1]Kolcio K,Breger L,Zetocha P.Model-based fault management for spacecraft autonomy[C]∥Proc.of the IEEE Aerospace Conference,2014:1-14.
[2]Nasir A,Atkins E M,Kolmanovsky I V.Mission-based fault reconfiguration for spacecraft applications[J].Journal of Aerospace Information Systems,2013,10(11):512-515.
[3]Liang W G,Zhou J L,Liu J Z.Fault diagnosis of spacecraft in long term management[C]∥Proc.of the International Astronautical Congress,2013:4613-4619.
[4]Bates D,Lee A,Meakin P,et al.Fault protection design and testing for the Cassini spacecraft in a“mixed”thruster configuration[C]∥Proc.of the AIAA Guidance,Navigation,and Control Conference,2013:1-10.
[5]Narasimhan S,Balaban E,Daigle M,et al.Autonomous decision making for planetary rovers using diagnostic and prognostic information[C]∥Proc.of the 8th IFAC Symposium on Fault Detection,Supervision and Safety of Technical Processes,2012:289-294.
[6]Issury I,Henry D,Charbonnel C.A boolean algebraic-based solution for multiple fault diagnosis:application to a spatial mission[J].Aerospace Science and Technology,2013,28(1):214-226.
[7]Hayden S C,Sweet A J,Christa S E.Livingstone model based diagnosis of earth observing one[C]∥Proc.of the AIAA Intelligent Systems Conference,2004:1-11.
[8]Dearden R,Ernits J.Automated fault diagnosis for an autonomous underwater vehicle[J].IEEE Journal of Oceanic Engineering,2013,38(3):484-499.
[9]Jin Y,Wang R X,Xu M Q.A fault diagnosis approach for spacecraft based on hierarchical transition system model[J].Acta Aeronautica et Astronautica Sinica,2013,34(2):401-408.(金洋,王日新,徐敏强.基于分层传递系统模型的航天器故障诊断方法[J].航空学报,2013,34(2):401-408.)
[10]Smaili R,El H R,Abdelkrim M N.Model-based process diagnosis:bond graph and signed directed graph tools[C]∥Proc.of the International Conference on Control,Decision and Information Technologies,2013:782-787.
[11]Reiter R.A theory of diagnosis from first principles[J].Artificial Intelligence,1987,32(1):57-95.
[12]Williams B C,Nayak P P.A reactive planner for a model-based executive[C]∥Proc.of the 15th International Joint Conference on Artificial Intelligence,1997:1178-1185.
[13]Zohar M,Amir P.The temporal logic of reactive and concurrent systems[M].New York:Springer,1992.
[14]Kurien J,Nayak P P.Back to the future for consistency based trajectory tracking[C]∥Proc.of the 17th National Conference on Artificial Intelligence,2000:370-377.
[15]Chang H,Jin T.Adaptive tracking controller based on the PID for mobile robot path tracking[C]∥Proc.of the 6th International Conference on Intelligent Robotics and Applications,2013:540-549.
[16]Zhao X F,Ouyang D T.New methods for deriving all minimal conflict sets in model-based diagnosis[J].Journal of Jilin University(Engineering and Technology Edition),2007,37(2):413-418.(赵相福,欧阳丹彤.基于模型的诊断中产生所有极小冲突集的新方法[J].吉林大学学报(工学版),2007,37(2):413-418.)
[17]Wang X Y,Ouyang D T.Conflict-based diagnosis of discrete event system[J].Journal of Jilin University(Engineering and Technology Edition),2013,43(2):380-385.(王晓宇,欧阳丹彤.基于冲突的离散事件系统诊断方法[J].吉林大学学报(工学版),2013,43(2):380-385.)
[18]Jiang Y F,Lin L.Computing the minimal hitting sets with binary HS-tree[J].Journal of Software,2002,13(22):2267-2274.(姜云飞,林笠.用对分-HS树计算最小碰集[J].软件学报,2002,13(22):2267-2274.)
[19]Zhou G,Feng W Q,Jiang B F.Computing minimal hitting set based on immune genetic algorithm[J].International Journal of Modelling,Identification and Control,2014,21(1):93-100.
[20]Qiu L,Liu Y,Song Y J,et al.A conflict diagnosis approach of changing sequences in gene ontology evolution[J].International Journal of Control and Automation,2014,7(6):269-284.
[21]Jin Y,Wang R X,Xu M Q.A spacecraft autonomous fault diagnosis approach for multiple fault-mode system based on qualitative models[J].Journal of Astronautics,2012,33(6):698-704.(金洋,王日新,徐敏强.基于分离策略的航天器多故障模式诊断方法[J].宇航学报,2012,33(6):698-704.)
[22]Wang R X,Jin Y,Xu M Q.The approach of fault diagnosis based on similarity degree matching distance function[J].Science China Technological Sciences,2013,56(11):2709-2720.
[23]Yang D X,Yuan T.Analysis on the application of feed-forward technology for space tracking,telemetering and control ships[C]∥Proc.of the 26th Conference on Spacecraft TT and C Technology in China-Shared and Flexible TT and C(Tracking,Telemetry and Command)Systems,2013:241-249.
E-mail:jinyang19840105@126.com
王日新(1963-),男,副教授,博士,主要研究方向为自主故障诊断、系统仿真。
E-mail:wangrx@hit.edu.cn
徐敏强(1961-),男,教授,博士,主要研究方向为自主故障诊断。
E-mail:xumq@hit.edu.cn
Spacecraft autonomous fault diagnosis method based on state memory
JIN Yang1,WANG Ri-xin2,XU Min-qiang2
(1.College of Aeronautical Engineering,Civil Aviation University of China,Tianjin 300300,China;2.Deep Space Exploration Research Center,Harbin Institute of Technology,Harbin 150080,China)
In order to avoid the unnecessary consumption of large amount of calculation caused by neglecting the influence of the last diagnostic result on the current diagnosis process in the traditional first principle theory based method when autonomous diagnosing,a new approach based on the state memory is proposed.By introducing the state memory mechanism into the traditional method,the meanings of diagnosis and conflict are extended.In order to obtain the general conclusions about diagnosis solution of the first principle diagnosis theory,the structure of the diagnostic results is analyzed,and the conclusions prove that the diagnosis efficiency of the new method is better than the traditional method.By introducing the“timestamp”and“state-lock”,the method can diagnose correctly with different input modes of observation autonomously.
fault diagnosis;the first principle;state memory;diagnosis efficiency
V 474
A
10.3969/j.issn.1001-506X.2015.06.34
金 洋(1984-),男,讲师,博士,主要研究方向为航天器自主诊断、系统仿真。
1001-506X(2015)06-1452-07
2014-04-16;
2014-11-16;网络优先出版日期:2014-12-09。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20141209.0120.006.html
国家重点基础研究发展计划(973计划)(2012CB720003);中国民航大学科研启动基金(2013QD02X)资助课题
