高中生物教学中数学模型建构探析
2015-08-16李春萍
李春萍

摘 要 新课标下生物教学中关于模型以及模型建构的价值是不容忽视的,结合数学模型建构的实例探讨在高中生物教学中渗透模型建构这种科学思维的方法及其意义。
关键词 数学模型 模型建构 建模思维
中图分类号:G633.91
文献标识码:A 文章编号:1002-7661(2015)07-0008-02
建构模型的方法,是高中课程标准和教材对学生提出的高于初中水平的科学方法和探究能力的要求,在高中阶段生物学课程的学习中,学生会陆续接触到物理模型、概念模型和数学模型等模型的建构,对模型方法会有比较全面的学习和了解。在此探讨一下在高中生物教学中数学模型的建构方法及其意义。
一、关于数学模型的认识
数学模型是用来描述一个系统或它的性质的数学形式,是根据具体情景,抽象出数学规律,并用公式或图表的形式表达。数学模型是联系实际问题与数学的桥梁,具有解释、判断、预测等重要功能。在科学研究中,数学模型是发现问题、解决问题和探索新规律的有效途径之一。引导学生建构数学模型,有利于培养学生透过现象揭示本质的洞察能力;同时,通过科学与数学的整合,有利于培养学生简约、严密的思维品质。在教学中我们往往重视对模型结论的运用,而忽视了建模方法的传授。其实,“授之以鱼不如授之以渔”,掌握了建构模型的方法才拥有认识世界的工具。下面以“建构种群数量增长的模型”为例谈谈建模的教学策略。
二、高中生物教学中建构数学模型的方法和步骤
数学模型的建构可以分为四个步骤。
第一步:模型准备。观察研究对象,提出问题,要建构一个数学模型,首先我们要了解问题的实际背景,明确建模的日的,并搜集必需的各种资料和信息,尽量弄清楚对象的特征。在这一数学模型的建构中,研究对象是“细菌”,其特征是“进行二分裂,每20min分裂一次”,建模的目的是探究细菌种群数量的变化特点,进一步解释生物现象,揭示生命活动规律。
第二步:模型假设。提出合理的假设是数学模型成立的前提条件,假设不同,所建立的数学模型也不相同。如本例中提到的假设是“在资源和空间无限多的环境中,细菌种群的增长不会受到种群密度增加的影响”,也就是在“理想”的环境中,此环境一般指的是“食物和空间条件充裕,气候适宜,没有天敌,没有疾病等”。该假设是对研究对象的一种简化,这是模型方法的基本思想的体现。
第三步:模型建构。根据实验数据,用适当的数学形式对事物的性质进行表达。根据所作的假设分析对象的因果关系,利用对象的内在规律和适当的数学工具,构造各个量词的等式关系。由细菌的二分裂特征,1个细菌分裂一次得到2个细菌,2个细菌第二次分裂得到4个细菌……通过归纳法得出细菌增殖的特点满足指数函数的形式进行增长,因此用数学形式表达为Nn =2n,其中N代表细菌数量,n表示第几代。这样的数学方程式科学、准确。
此外,还可以根据刚才的指数函数模型把细菌的数量进行计算,把数据进行整理,此时构建出另一种数学模型——表格。
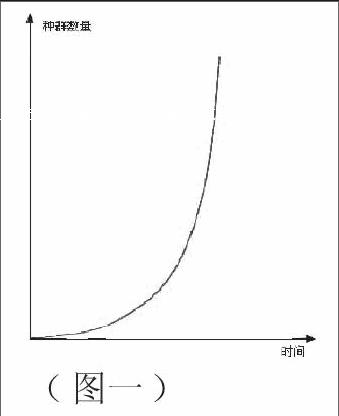
由于表格的形式具有一定的局限型,因此我们还可以把它构建成坐标图的数学模型,这样的曲线图是数学模型的另一种表现形式,它能更直观地反映出种群数量的增长趋势,即“J型增长曲线”。(图一)
第四步:模型检验和修正。通过进一步实验或观察等,对模型进行检验或修正。在理想状态下细菌种群数量增长的数学模型是比较简单的,而生物学中大量现象与规律是极为复杂的,存在着许多不确定因素和例外的现象,需要通过大量实验或观察,对模型进行检验和修正,使学生认识到模型的构建是一个不断发展和完善的过程。
可设计以下问题情景:
(1)其它的生物并不一定进行二分裂的生殖方式,那么它们的种群数量的变化是否也满足上述的“J型增长曲线”呢?如果满足那么要建立它的函数模型又是怎样呢?进一步讨论:能不能根据细菌增长的方程式推导成一个反映一般的种群和细菌种群增长类似的种群增长的方程式?通过进一步的假设分析可以得出:自然界确有类似细菌在理想条件下种群数量增长的形式,得到Nt = Noλt,其中No为该种群的起始数量,t为时间,Nt为t年后该种群的数量,九为该种群数量是一年前种群数量的倍数。
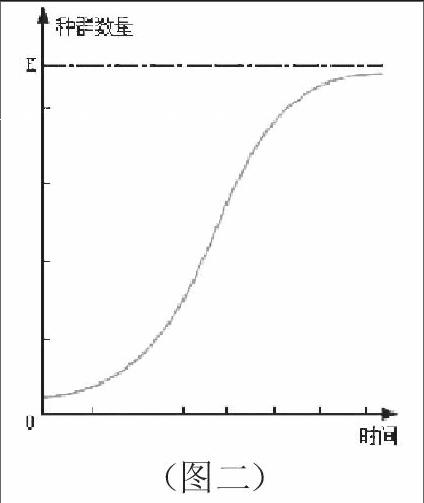
(2)生物的实际生活环境是否真的这么理想呢?让学生对在实际环境(如资源和空间有限,气候并不一直适宜,出现天敌和竞争者,同时还会受到疾病等的威协等)中生物种群的数量变化进行进一步的假设分析,得出在自然界中,种群不能无限增长,受到各种生态因素的制约,而且随着种群数量的不断增长,制约因素的作用也在增大,使出生率和死亡率一般来说变成平衡的,种群总是在增长到一定限度后达到相对的稳定,因此构建出另一增长曲线——“S型增长曲线”。(图二)
分别让学生建立“J”型增长曲线和“S”型增长曲线的增长率和增长速率的曲线图模型。
“J”型曲线的“增长率”和“增长速率”和时间的关系曲线
总结种群增长数学模型的建构过程:观察研究对象一提出合理假设一数学表达一检验、修正。以上建立具体数学模型的过程,就是一个从具体的生物现象Lj规律建立抽象的数学模型,又用抽象的数学模型来解释具体的生物学现象L规律的过程。在这一过程中学生学会了从现象中揭示出本质和规律,同时学会运用恰当的数学模型表达某些生物学规律的创造性思维方法。模型的建立过程就是一个科学探究的过程。“大胆假设,小心求证”的科学思维贯穿其中。这种思维方法,一旦内化为学生自己的认知模式,就能获得认知水平的飞跃。
参考文献:
[1]汪忠.高中生物课程标准(实验)解读[M].江苏教育出版社,2004.
[2]于梅.在新课标实施中切实加强模型方法的教育[J].中学生物教学,2007,3.
(责任编辑 全玲)
