一种改进的遗传算法在边坡工程中的应用

王华俊，卿翠贵，姚文杰

（浙江省工程勘察院，浙江 宁波315012）

由于滑坡的危害大、治理难、费用高等特点，土坡稳定分析成为一个非常重要的问题［1］。极限平衡法虽然不能考虑土体的应力-应变关系，但是由于极限平衡法在工程中长期应用，概念简单明确，各行业中均有大量的经验积累，目前在工程界极限平衡法是边坡稳定性分析中最常用的方法［2］。极限平衡法中，确定最小安全系数以及对应的滑裂面形状是稳定性分析中的关键工作。由于边坡稳定性安全系数求解涉及到复杂的边坡形状、土体材料参数和水文地质环境，因此它的目标函数是多峰的或者是很不规则的优化问题，在搜索过程中很容易陷入局部最优解［3］。遗传算法是一种随机搜索和优化方法，适合求解非线性多极值问题，具有较强的全局搜索能力，因而被广泛的应用于边坡稳定性分析中［4］。

1 遗传算法

遗传算法（Genetic Algorithm）是借鉴自然界生物进化理论产生的优化计算方法［5］。1975年约翰·霍兰德首先在其论著［6］中提出遗传算法的基本概念。在国内，肖专文和张奇志［7］最早将基本遗传算法应用于边坡稳定性分析，随后很多学者对其进行了改进［8-10］。边坡稳定性这类工程寻优问题，每个解向量好比一个染色体，而解向量中的每一个分量犹如染色体中的每个基因，在边坡形状和土体参数确定的情况下，边坡安全系数完全由旋转中心的横坐标x、旋转中心纵坐标y和旋转半径R这3个参数确定，可将x，y，R分别看作是染色体（x，y，R）的一个基因，解向量（x，y，R）对应的安全系数Fs越小，认为组解对这个寻优问题的适应性越好，给予这组解更大的概率进入下一代，从而模拟自然选择的过程。其计算流程如图1所示。

图1 遗传算法计算流程

（1）初始化种群

遗传算法在计算之前必须先产生一组初始种群（Initial Population），用于接下来的计算操作。一般来说初始种群是随机产生的决策变量。

（2）选择操作（Selection）

本文采用比例选择方式，其特点是：各个个体被选中的概率与其适配度大小成正比［11］。也叫赌轮（Roulette Wheel）选择，和赌博中的赌盘操作原理类似［12］。

（3）交叉操作（Crossover）

根据预先设定的杂交率Pc决定是否进行基因交换以产生新的子代。本文采用单点交叉，首先产生一个在区间［0，1］上服从均匀分布的随机数，若此随机数小于交叉率Pc，则进行交叉操作，交叉后的子代基因按下面公式生产。

其中：t是进化代数，rand～U（0，1）

（4）变异操作（Mutation）

判断是否变异和判断是否杂交的过程一样，即产生的随机数若小于变异率Pm则进行变异操作。变异机制是产生新个体的一种方式，避免了提早收敛、陷入局部解的困境，维持物种多样性。

（5）适配度函数（Fitness Function）

适配度函数的作用是评价每一个染色体的好坏，从而对接下来模拟生物选择竞争提供参考。一般在遗传算法中规定，适配度函数值大于等于零，且越大表示该决策向量越接近最优解。

（6）编码及编码方式

遗传算法运算对象是符号串，因此必须把决策向量编译成遗传算法能够进行操作的信息，这个过程就是编码（Code）。本文采用十进制编码。

（7）最优保存策略

所谓最优保存策略［13］，有的文献也将其称为优体克隆［14］，即对适配度最大的若干个染色体不进行杂交和变异，而是完整的复制到下一代，它避免了最优染色体在杂交和变异的过程中丢失，从而使求得的最小安全系数不会随着繁殖代数的增加出现变大的情况，保证进化过程中不会出现返祖现象。

2 基本遗传算法的缺陷

基本遗传算法应用于边坡稳定性问题中时存在很多缺陷。一方面，基本遗传算法局部寻优能力较差，对各种实际问题搜索空间大小变化适应能力差［15］，计算量大，基本遗传算法搜寻到全局最优解需要较大的进化代数和花费较长的计算时间。另一方面，边坡稳定性安全系数求解涉及到复杂的边坡形状、复杂的土体材料参数和水文地质环境。因此它的目标函数是多峰的或者是很不规则的优化问题，在搜索过程中很容易陷入局部最优解，从而过早收敛。

3 遗传算法的改进

边坡稳定性最小安全系数计算问题中以往对遗传算法的改进过程，杂交率和变异率是固定不变的，而杂交率和变异率对遗传算法来说是两个非常关键的运行参数，他们直接关系到遗传算法的收敛性和运算速度。如何确定最合理参数需要反复试验，这是一件繁琐的工作。本文采用动态的杂交率和变异率来改进遗传算法在边坡最小安全系数搜索的性能。本文认为，交叉率和变异率不仅和选中杂交或变异的染色体的适配度在整个种群的染色体适配度水平有关，还和其所在的进化代数有关。交叉率或变异率和选中染色体的适配度有关的原因是：杂交率和变异率决定着种群中的染色体是否被破坏，如果杂交率较高，两个被选中用来杂交的染色体被杂交的可能性就高，在同一个种群中，有的染色体的适配度高，我们希望其染色体尽量少遭到破坏，有的染色体适应性不好，希望其通过杂交或变异改善其性能。因而，根据染色体的适配度在整个种群中适配度的水平来决定其杂交率和变异率是合理的做法。杂交率和变异率与个体所处的进化阶段的原因是：随着进化代数的增加，种群的平均适配度越来越高，种群的整体素质越来越好，因而到进化后期，应该减小对优秀个体的破坏，所以杂交率和变异率应该越来越小以减小对后期优秀染色体的破坏，从而加快收敛速度。

（1）杂交操作的改进

本文对杂交率的动态调整公式为：

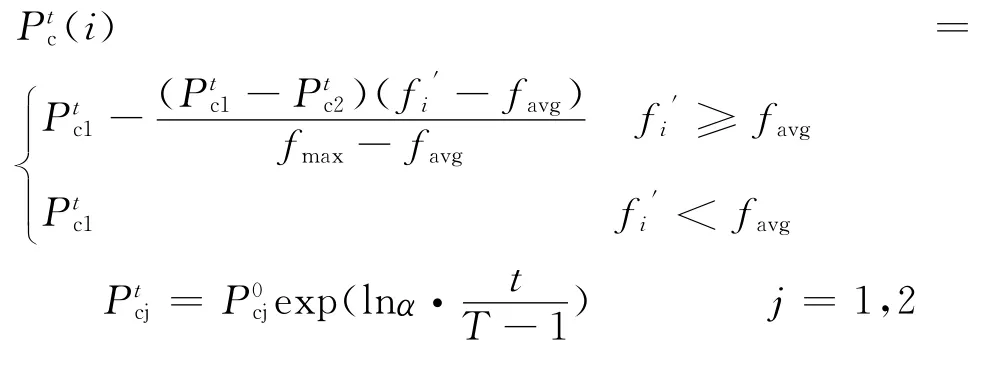
其中：t是当前进化代数（i）是第t代第i组待杂交染色体的动态杂交率是第t代整个种群的最大杂交率；是第t代整个种群的最小杂交率是第i组两个选中待杂交染色体的适配度的较大值；fmax是整个种群的最大适配度；favg是整个种群适配度的平均值。式中，当j=1时即t代整个种群的最大杂交率，当j=2时即t代整个种群的最小杂交率即初代种群进化时的最大杂交率是倒数第二代即第T-1代种群进化时的最大杂交率。同理即初代种群进化时的最小杂交率是倒数第二代即第T-1代种群进化时的最小杂交率。定义为杂交率伸缩系数。杂交率的动态调整图形如图2和图3所示。

图2 第t代种群动态杂交率调整曲线

图3 每代最大（最小）杂交率随代数变化

（2）变异操作的改进

本文提出动态杂交率的公式为：

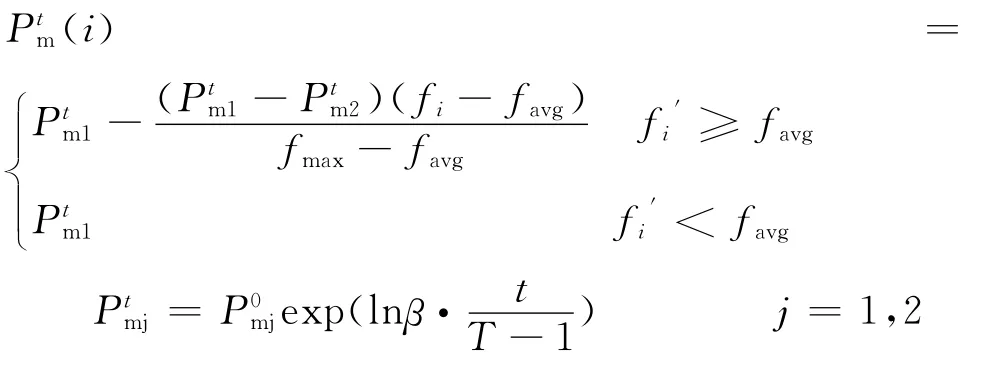
4 改进遗传算法的程序实现

首先，本文采用十进制编码方式，将安全系数的n次方的倒数作为适配度值，采用最优保存策略防止杂交和变异过程中最优解被破坏，用C＃语言编写了改进遗传算法的程序。其次采用Fortran语言编写了条分法边坡稳定性分析的程序。最后用C＃语言编写了边坡参数和遗传算法计算参数的输入窗体和计算结果输出窗体。采用的开发工具是基于.Net Framework平台的VS2010。本程序的特点是应用了面向对象的设计方法，遵循软件工程中界面逻辑和业务逻辑分离的原则，采用了C＃和Fortran混合编程方式，充分发挥C＃语言开发界面上的优势和Fortran语言科学计算上的优势。

5 算 例

某山体由于开挖形成边坡，岩土体主要分为3层，顶层为第四系残坡积层，下面两层依次是全风化凝灰岩和强风化凝灰岩。边坡某剖面如图4所示。

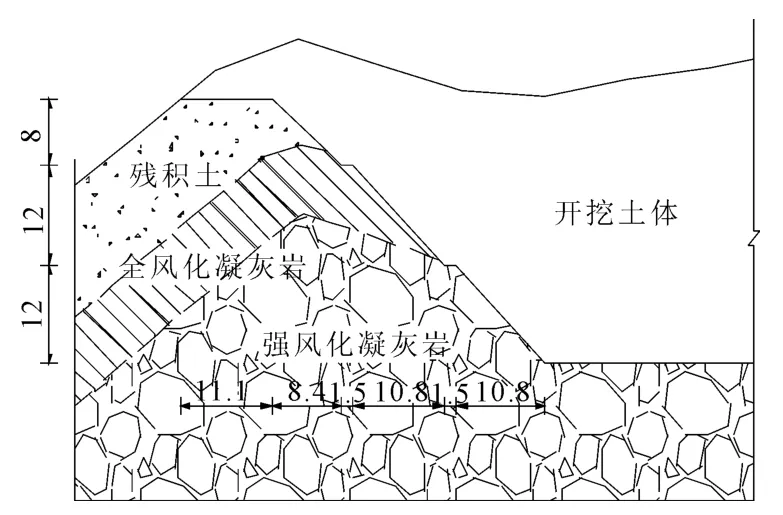
图4 边坡断面示意图（单位：m）

该边坡主要土层参数如表1所示。

表1 主要土层的物理力学性质参数

本文采用的安全系数计算方法是Bishop法，分别采用区格搜索法、基本遗传算法和改进遗传算法搜索最危险滑动面，搜索范围：X（m）：45～60，Y（m）：20～35，R（m）：15～40。采用基本遗传算法时，设置种群尺寸M=100，最终进化代数T=200，杂交率Pc=0.7，变异率Pm=0.01，采用最优保存策略，精英染色体的个数为2个。采用改进遗传算法时，设置种群尺寸M=100，繁殖代数T=200，杂交率Pc1=0.9，Pc2=0.5，杂交率伸缩系数α=0.6。变异率Pm1=0.1，Pm2=0.01，变异率伸缩系数β=0.6，采用最优保存策略，精英染色体的个数为2个。基本遗传算法搜索时平均安全系数和最小安全系数随进化代数变化的图形如图5所示，改进遗传算法搜索时平均安全系数和最小安全系数随进化代数变化的图形如图6所示。两种算法最小安全系数随进化代数的变化曲线如图7所示。

图5 基本遗传算法安全系数随进化代数变化曲线

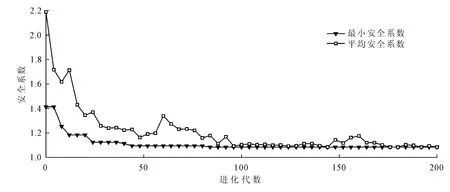
图6 改进遗传算法安全系数随进化代数变化曲线

图7 两种遗传算法最小安全系数随进化代数变化对比

基本遗传算法搜索到的最小安全系数是1.130，改进遗传算法搜索到的最小安全系数是1.084。而采用Geo-Slope软件计算的传统区格搜索法搜索到的最小安全系数是1.281。可以看出采用遗传算法相比传统的区格搜索法能够搜索到更小的安全系数，而改进后的遗传算法搜索到的安全系数比基本遗传算法更小。

6 结 论

（1）遗传算法能有效的克服传统方法搜索最小安全系数可能陷入局部极值的缺陷，在边坡最小安全系数搜索中相比传统的区格搜索方法具有更好的搜索效果。

（2）改进后的遗传算法在边坡最危险滑动面搜索中具有更好的性能，有效改善了基本遗传算法易于陷入早熟的缺点，具有更强的全局搜索能力和收敛能力。

［1］杨天鸿，张锋春，于庆磊，等.露天矿高陡边坡稳定性研究现状及发展趋势［J］.岩土力学，2011，32（5）：1437-1451.

［2］朱大勇，卢坤林，台佳佳，等.基于数值应力场的极限平衡法及其工程应用［J］.岩石力学与工程学报，2009，28（10）：969-975.

［3］万 文，曹 平，冯 涛，等.一种自由搜索边坡最危险滑动面的新方法［J］.中南大学学报：自然科学版，2006，（4）：810-814.

［4］李南生，唐 博，谈风婕，等.基于统一强度理论的土石坝边坡稳定分析遗传算法［J］.岩土力学，2013，（1）：243-249.

［5］韩瑞锋.遗传算法原理与应用实例［M］.北京：兵器工业出版社，2010.

［6］Holland J H.Adaptation in natural and artificial systems：An introductory analysis with applications to biology，control，and artificial intelligence［M］.U Michigan Press，1975.

［7］肖专文，张奇志，梁 力，等.遗传进化算法在边坡稳定性分析中的应用［J］.岩土工程学报，1998，（1）：44-46.

［8］金菊良，丁 晶，魏一鸣.加速遗传算法在地下水位动态分析中的应用［J］.水文地质工程地质，1999，（5）：6-9.

［9］丰土根，刘汉龙，高玉峰，等.加速遗传算法在边坡抗震稳定性分析中的应用［J］.水利学报，2002，（9）：89-93.

［10］李延梅.一种改进的遗传算法及应用［D］.华南理工大学，2012.

［11］阙金生，陈剑平，王 清，等.遗传算法在土坡稳定性分析中的应用［J］.岩土力学，2008，29（2）：415-419.

［12］解可新，韩 健，林友联.最优化方法［M］.天津：天津大学出版社，2004.

［13］毕惟红，任红民，吴庆标.一种新的遗传算法最优保存策略［J］.浙江大学学报：理学版，2006，33（1）：32-35.

［14］何朋朋，姚磊华，汤荣贵.基于改进的遗传算法边坡稳定性分析方法及其应用［J］.地质灾害与环境保护，2007，18（1）：100-104.

［15］熊伟清，魏 平，赵杰煜.遗传算法的早熟现象研究［J］.计算机应用研究，2001，18（9）：12-14.