考虑界面滑移的组合板承载特性

史晓宇

（上海建筑设计研究院有限公司，上海200041）

压型钢板与混凝土界面的纵向剪切-黏结破坏是组合板最为常见的破坏方式。界面滑移的累积效应体现为组合板端部压型钢板和混凝土的相对滑移。我国《组合楼盖设计与施工规程》［1］（CECS273：2010）和欧洲规范EC4［2］建议组合板的弹性挠度可以根据构件截面抗弯刚度按照结构力学方法计算。

《组合楼盖设计与施工规范》［1］（CECS273：2010）关于组合板挠度计算的规定与欧洲规范EC4［2］有以下两点较大不同：第一，EC4的规定适用于连续板中间跨的挠度计算，我国规范未限制适用范围；第二，EC4规定：初始滑移荷载（即端部滑移0.5mm时的荷载）超过使用阶段荷载1.2倍时可不考虑连续板端跨的端部滑移，否则需考虑连续板端跨的端部滑移效应，并增加端部锚固措施。

界面滑移导致的端部滑移对组合梁、板的承载特性有重要的影响。Johnson［3］研究了组合梁端部滑移对其挠度的影响。指出简支组合梁跨中弯矩可由三部分组成：

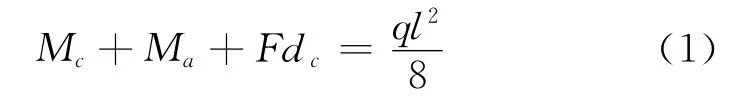
式中：Mc为混凝土部分贡献的抗弯能力；Ma为钢梁部分贡献的抗弯能力；F代表交界面的纵向剪力；dc为两部分截面合力位置的距离；q为梁上承受的均匀荷载集度；l为梁跨度。算例指出：完全共同作用组合梁（即不考虑界面滑移），由界面剪力产生的抗弯承载力的贡献可达到75%，其他两部分之和为25%。考虑界面滑移时，部分连接作用的组合梁由界面剪力产生的抗弯承载力的贡献减小到72%，由此会导致组合梁挠曲线曲率增大约13%。Poh和Attard［4］指出端部滑移会导致组合板的刚度和承载能力出现大幅度下降，认为组合板界面剪力可模拟为纵向剪力和支座处摩擦力的共同效应。

参考部分连接方法的规定，同时考虑端部锚固栓钉对界面滑移的限制作用，在组合楼板剪切-黏结破坏的三维非线性有限元模型及试验数据的基础上，进行了考虑界面滑移和端部锚固影响的组合板承载特性分析。提出了简支板和端部锚固组合板挠度计算的相关建议。

1 简支组合板挠度理论计算

受弯构件的挠度可由弯矩-曲率关系通过积分法得出：

式中：Ec为混凝土弹性模量；Ieq为组合截面等效惯性矩；ρ为计算截面的板底曲率半径；M为受弯构件承受的弯矩。

选取了史晓宇等［5］的试验数据进行对比验证。共进行了13块组合板的足尺弯曲试验，其中8块为无端部锚固组合板，其余5块组合板均采用栓钉穿透钢板与支承钢梁焊接的端部锚固形式。表1为试验构件编号和基本参数。试验采用开口型3DDECK压型钢板，试验加载装置和压型钢板的几何形状如图1所示。

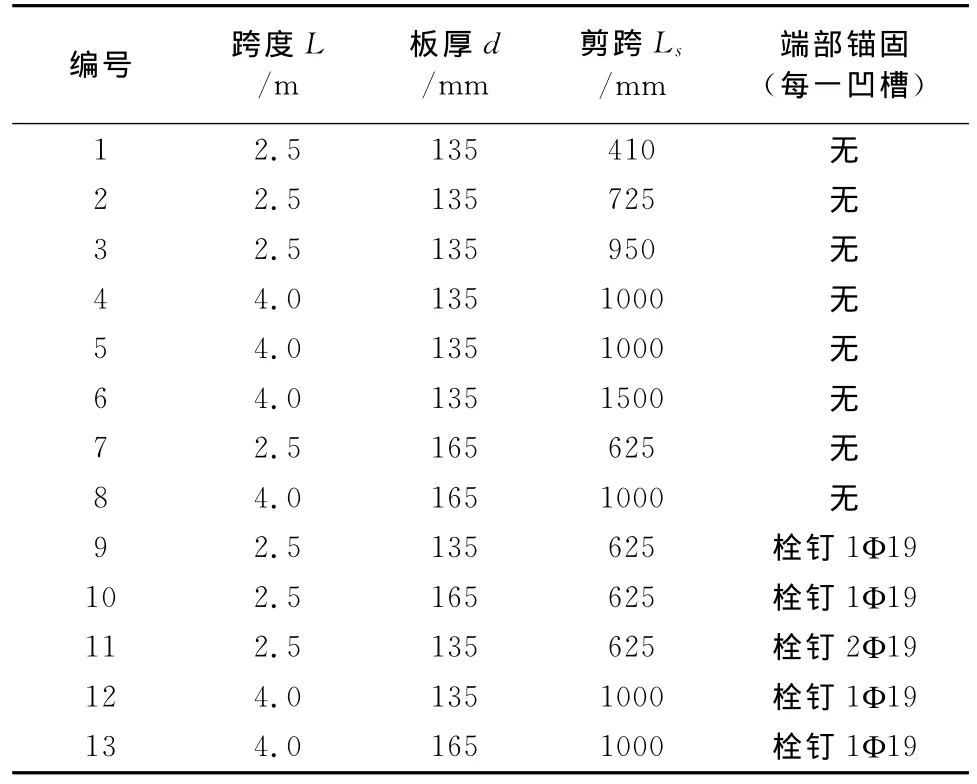
表1 组合板试件分类及编号

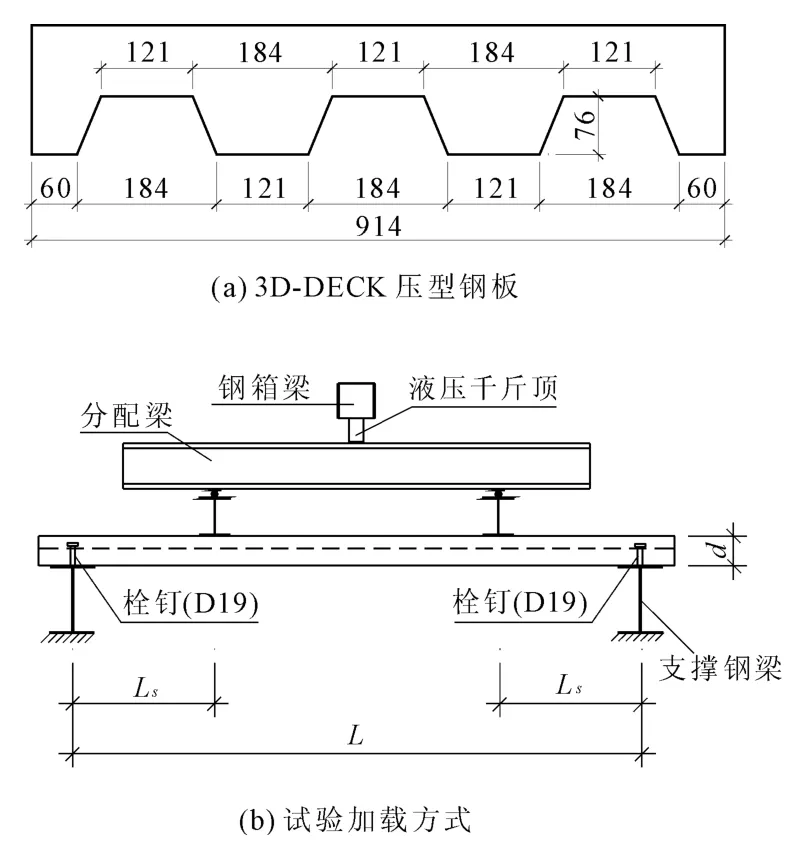
图1 试验装置及压型钢板板型

根据试验所用构件的边界条件和加载方式，考虑挠曲线曲率的数学表达，图2中简支梁在集中荷载下的弹性挠度可表示为：

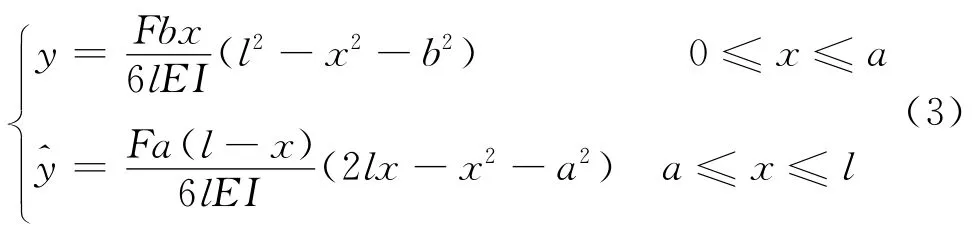
式中：F为集中荷载；x为构件沿轴线坐标；y为构件弹性挠度值；l为梁跨度；a、b为集中荷载作用点至梁支座的距离，如图2所示。两点加载的构件弹性挠度可按照叠加原理由式（3）求得。

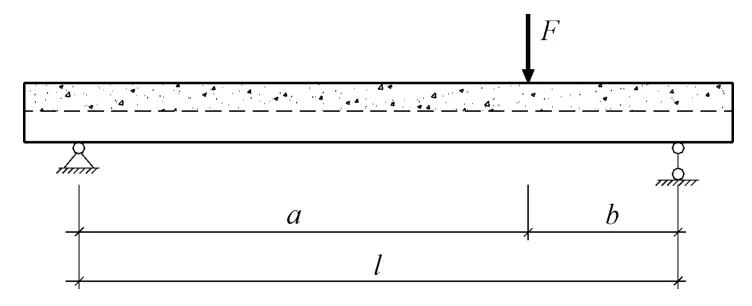
图2 简支梁计算模型

2 有限元分析模型简介［6］

建立了压型钢板-混凝土组合板的有限元分析模型。将钢板与混凝土接触面的相互作用模拟为带有黏滞力和摩擦作用的接触问题。模型选用通用有限元分析软件ANSYS，考虑了几何非线性和材料非线性。混凝土采用三维8节点实体单元（Solid 65），压型钢板采用4节点空间壳单元（Shell 181）。

采用面-面接触分析模拟压型钢板与混凝土交界面处的相互作用。接触单元采用Targe170和Conta173单元。滑动接触时，交界面的切向应力满足下式所示的库伦摩擦模型：

式中：τ为切向应力；τc代表交界面的黏滞力；μ为摩擦系数；P为界面的法向应力。

图3为弯曲试验有限元分析模型，考虑构件和受力的对称性，计算中取1／2板模型。有限元分析模型限制了铰支座处钢板节点三个方向的平动自由度，位移荷载施加于板顶部加载处的混凝土节点之上，模拟试验中的分布梁两点加载。

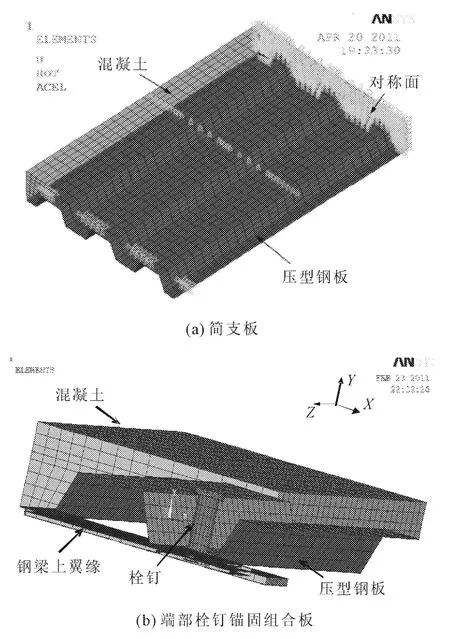
图3 组合板弯曲试验有限元分析模型

表2为组合板极限承载力的试验与有限元分析结果对比。试验与有限元分析结果的比值Ptest／Pfe的均值为1.015，标准差为0.089，总体吻合较好。由此可见，有限元模型中采用的考虑黏滞力和摩擦作用的库伦摩擦模型可以用来描述组合板中钢板与混凝土交界面的纵向剪切-黏结特性。

3 组合板挠度计算的对比及讨论

根据规范要求，选取试验所用试件的参数，进行了使用阶段荷载作用下组合板弹性挠度的分析。对试验数值、理论计算值和有限元分析结果进行对比讨论。

3.1 简支组合板

表3为简支组合板弹性挠度计算结果的对比。选取有代表性的简支板，进行了理论值、有限元分析结果与试验值的对比。长细比为试件剪跨长度Ls与有效高度dp的比值，有效高度为组合板受压翼缘到压型钢板形心的距离。

表2 组合板极限承载力的试验与有限元分析结果对比

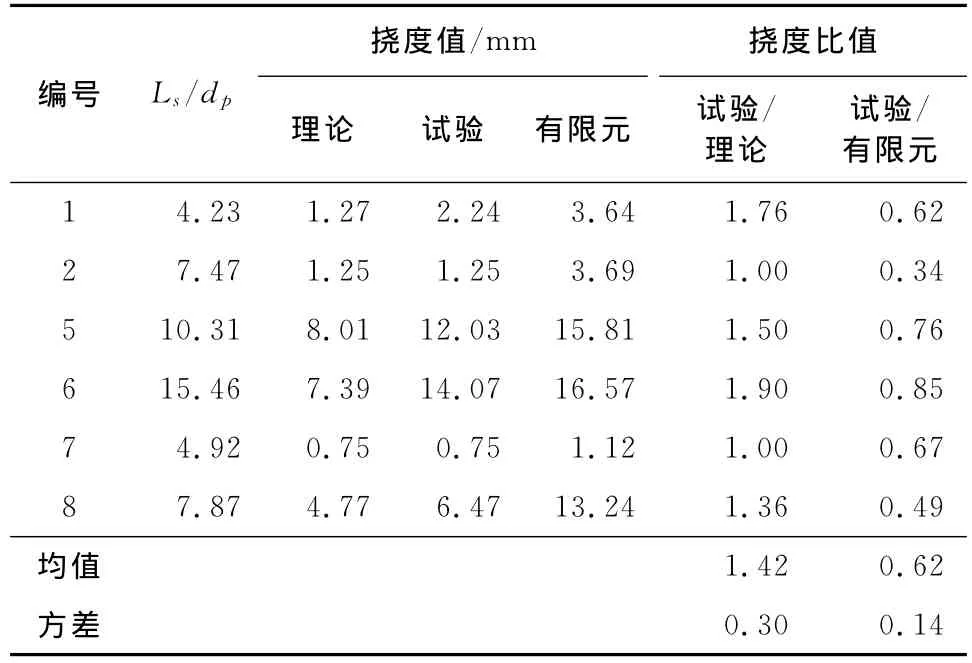
表3 简支组合板弹性挠度分析结果对比

表3中数据表明，由于未考虑界面滑移的影响，《组合楼盖设计与施工规范》［1］（CECS273：2010）建议的弹性挠度计算值远低于试验值，且数据离散较大。试验值与理论值比值的均值为1.42，方差达到了0.30。由于组合板的界面滑移主要发生在剪跨范围之内，大剪跨试件6的长细比15.46，试验值与理论值的比值达到了1.90。有限元分析结果也表明，承载能力接近的情况下，构件的挠度值远大于理论计算值。对简支组合板的情况，规范建议的理论计算值不够安全。

3.2 端部锚固栓钉对组合板挠度计算值的影响

端部锚固栓钉作为现行《高层民用建筑钢结构技术规程》［7］要求的构造措施，在组合板中应用极广。研究表明，端部锚固栓钉的使用可以明显地改善组合板的承载能力和变形能力。

表4为端部锚固简支组合板弹性挠度计算结果的对比。表中数据表明，带有端部锚固栓钉的组合板弹性挠度的发展较为有规律，试验值、理论计算值与有限元分析结果吻合较好。试验值与理论值比值的均值为1.01，方差为0.18。

表4 端部锚固组合板弹性挠度分析结果对比

图4为端部锚固组合板的弹性挠度与长细比的关系，并对各类结果进行了线性拟合，图中“线性”表示线性拟合，R2为线性拟合的相关系数。图中显示：随长细比增大，板的弹性挠度相应增加。理论计算值介于试验值和有限元分析结果之间，三者的发展趋势一致，差距满足工程需要。

图4 端部锚固组合板弹性挠度与长细比关系

3.3 端部锚固栓钉对组合板界面特性的影响

端部锚固栓钉对组合板的界面滑移有明显限制作用，由此会引起界面滑移及摩擦应力的相应变化。图5为组合板界面滑移沿跨度的典型分布情况。无端部锚固试件的界面滑移由跨中向端部逐渐增大，极限状态下剪跨内的滑移分布比较均匀；端部锚固试件的界面滑移沿试件跨度分布较均匀，跨中非剪跨范围也有相当的发展。

界面摩擦应力的典型分布见图6。与界面滑移的规律一致，极限状态下无端部锚固试件界面摩擦应力除支座位置由于支座反力的影响较大外，也从端部向跨中逐渐减小，剪跨内分布较均匀，大部分数值在0.05MPa以下；端部锚固试件的界面滑移受到限制，界面摩擦应力在跨中纯弯段也有相当的发展，且相当一部分数值在0.05MPa以上，如图6（b）所示。界面摩擦应力分布范围和数值的提升会带来界面剪切-黏结能力的充分发挥，使端部锚固试件的纵向抗剪能力大为提高。由于栓钉的影响，极限状态下，端部锚固组合板界面摩擦应力的峰值出现在栓钉影响区域的内侧，而非简支板中的支座位置。

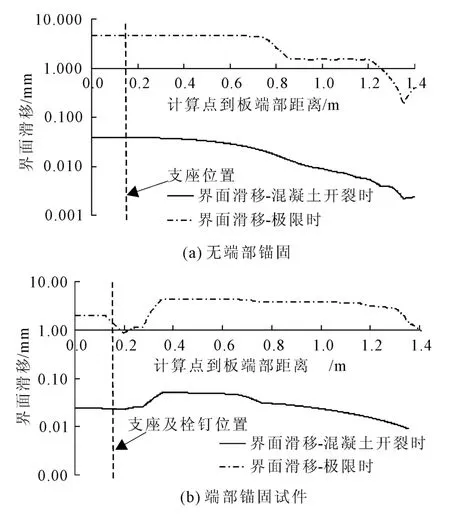
图5 组合板界面滑移沿跨度典型分布

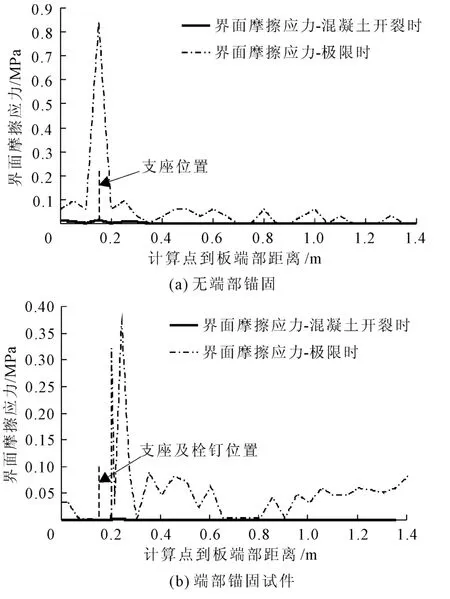
图6 组合板界面摩擦应力沿跨度典型分布

4 总 结

建立了组合板剪切-黏结破坏的有限元分析模型，结合试验、有限元模拟和理论分析，提出了考虑界面滑移的组合板弹性挠度的计算建议。研究得到以下主要结论：

（1）提出的有限元分析模型与弯曲试验的结果总体吻合较好。这种基于非线性接触分析的通用的有限元分析方法可以用来预测组合板的剪切-黏结承载特性。

（2）现行《组合楼盖设计与施工规范》［1］（CECS273：2010）关于弹性挠度的规定未考虑界面滑移的影响，与欧洲规范的规定相比不够安全。

（3）由于端部锚固栓钉的有利影响，组合板的弹性挠度发展与理论计算值较为接近，且具有规律可循。

（4）为保证设计的可靠性，考虑界面滑移的影响，参考表3和表4的分析结果，建议按照我国规范计算的简支组合板弹性挠度计算值应放大1.5倍，端部锚固组合板的计算值宜放大1.2倍。

［1］中国工程建设协会.CECS273：2010.组合楼板设计与施工规范［S］.北京：中国计划出版社，2010.

［2］EC 4：Design of composite steel and concrete structures，Part 1.1：General rules and rules for buildings［S］.EN1994-1-1：European Committee for Standardization.Brussels，2004.

［3］Johnson R P.Composite structures of steel and concrete beams，slabs，columns，and frames for buildings［M］.3rd.ed.Malden，MA：Blackwell Pub.，2004.

［4］Poh K W，Attard M M.Calculating the load-deflection behavior of simply-supported composite slabs with interface slip［J］.Engineering Structures，1993，15（5）：359-367.

［5］史晓宇，陈世鸣，裘子豪.组合板剪切-粘结机理及承载能力试验［J］.同济大学学报：自然科学版，2012，40（5）：666-672.

［6］Shiming Chen，Xiaoyu Shi.Shear bond mechanism of composite slabs-A universal FE approach，journal of constructional steel research［J］.2011，67（10）：1475-1484.

［7］中华人民共和国建设部.JGJ 99-98.高层民用建筑钢结构技术规程［S］.北京：中国建筑工业出版社，1999.