构造虚拟闭合电路 求解感生电动势

王松涛

（中山市华侨中学 广东 中山 528400）

【例1】如图1，半径为R的圆形区域内有随时间变化的匀强磁场，磁感应强度随时间均匀增加的变化率为k（k为常量），磁场方向与圆形区域垂直，在图中垂直纸面向里.一长为2R 的金属直杆ac 处在圆形区域所在平面，ab 段正好在磁场内，bc 段位于磁场外，且ab＝bc＝R，求杆中的感应电动势.

图1

要解决这一问题，首先回到电动势这一概念的定义.所谓电动势就是把单位正电荷从电源负极经电源内部移动到电源正极非静电力所做的功.根据麦克斯韦电磁场理论，变化的磁场产生感生电场.电荷在感生电场中受到感生电场力，感生电场力等于电荷的电荷量与感生电场强度的乘积，F＝qE感，与感生电动势对应的非静电力就是感生电场力，故ac棒的感生电动势为

但直接去求感生电动势需要求出ac 棒上各点的感生电场强度，同时还需要进行积分，非常复杂.如果能够构造一个包含该部分导体的闭合电路，就可以利用法拉第电磁感应定律进行求解了.

根据对称性，圆形区域内的磁场磁感应强度均匀增大的过程中，纸面内的感生电场的电场线是一系列沿逆时针方向的同心圆，如图2所示.

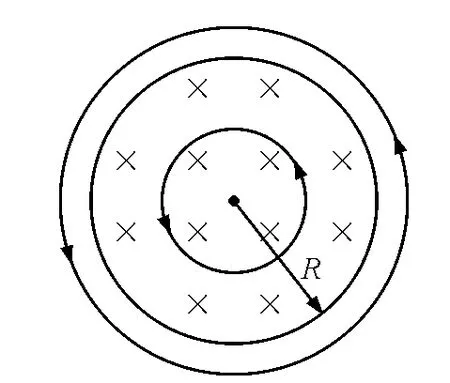
图2

先求棒ab 部分的感生电动势.构造虚拟的闭合电路Oab 如图3所示，闭合电路的感生电动势

由于感生电场强度的方向与Oa 和bO 垂直，即沿Oa 和bO 移动电荷时，感生电场力不做功，故

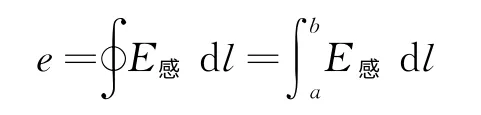
由法拉第电磁感应定律闭合电路的感生电动势

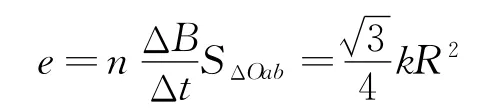
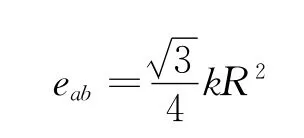
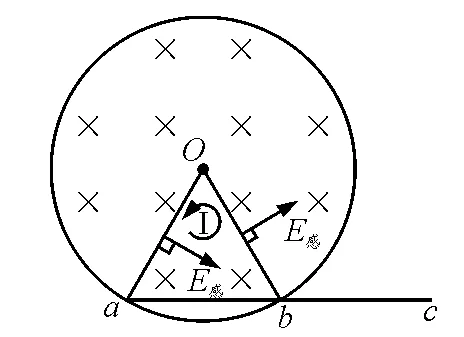
图3

棒bc 部分处于磁场区域之外有没有产生感生电动势呢？构造虚拟的闭合电路Obc 如图4所示.由于感生电场强度的方向与Ob和cO 垂直，即沿Ob和cO 移动电荷时，感生电场力不做功，故

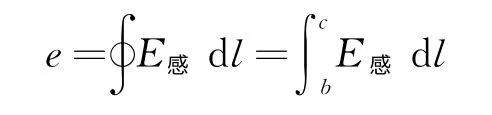
由法拉第电磁感应定律闭合电路的感生电动势

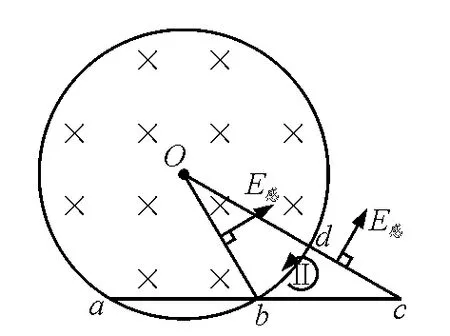
图4

棒ac 的感生电动势

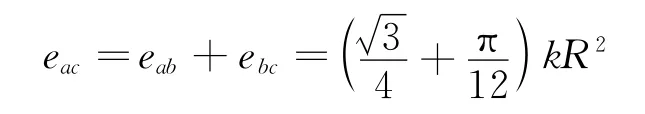
事实上，可以构造虚拟闭合电路Oac 直接求出棒ac 的感生电动势.如图5，有

其中

显然计算结果相同.这表明导体棒ac 产生的感生电动势与如何构造假想的闭合电路并无关系.根据麦克斯韦电磁场理论，均匀变化的磁场产生稳定的感生电场，这一感生电场与闭合电路存在与否无关，通过本例正好印证了这一点.

图5

【例2】如图6所示，用均匀导线做成的长方形线框abcd 中，ab＝cd＝L，ad＝bc＝2L，e，f分别为bc 与ad 的中点，在长方形线框的左半部分abef 区域内有垂直于纸面向里的匀强磁场，磁感应强度随时间均匀增加，其变化率为k，则e和f 两点间的电势差为多少？

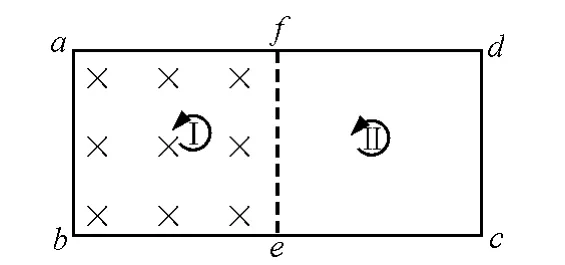
图6

图7

解析：本例见诸于各类习题资料中，但存在着许多混乱与错误，其中最常见的是认为线框fabe 段处在变化的磁场中，相当于电源，产生感生电动势，而线框ecdf 段处于变化的磁场之外，相当于外电路，不产生感生电动势.那么事实怎样呢？

根据法拉第电磁感应定律闭合电路的感生电动势

那么线框fabe 段产生的感生电动势就是整个闭合电路的感生电动势吗？构造如图7所示的虚拟的闭合电路fabef，根据对称性可判断，正方形闭合电路fabef 的4条边对应的感生电动势大小相等，则fabe段感生电动势为

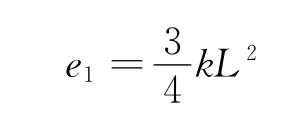
而对长方形线框dabcd 来说，总的感生电动势等于左右两部分线框感生电动势之和，故右半部分线框ecdf 的感生电动势为

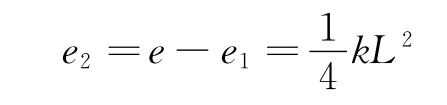
如果构造虚拟的闭合电路fecdf，计算结果一致，同样说明某部分导体产生的感生电动势与所假想的闭合电路无关，这正是麦克斯韦电磁场理论的本质要求.

近年来，高考提高了对感生电场的考察，例如2012年福建卷的第22题、2014年安徽卷的第20题等.只有经历从看得见的具体有形的闭合电路到假想的虚拟的闭合电路去理解感生电动势的产生，才能逐步体会到均匀变化的磁场所产生的稳定的感生电场的客观存在性.只有经历这种从具体到抽象的思维上升，也才算是初步正确认识到电磁感应的实质，从而更好地适应高考的能力要求.