基于广义Henon映射以及CNN超混沌系统图像加密方案

赵国敏, 李国东

(新疆财经大学, 新疆 乌鲁木齐 830012)

0 引言

随着计算机及互联网技术的快速发展，网络传输信息量和速度随之发展，现今网络传输速度之快及信息量之大令人惊叹，但网络发展的背后随之带来的信息安全问题也越来越受到关注.由于数字图像具有信息丰富、数据量大、冗余度高及像素之间相关程度高等特点，因而数字图像已广泛渗透到我们生产生活的各个领域，并一度成为人们表达信息的重要方式之一.为防止第三方对传输图像的窃取和破坏，需要设计更加缜密的图像加密方案.

针对图像加密问题，学者们提出了各式各样加密技术，总结现有的图像加密技术主要包括：1)传统加密技术，如DES(数据加密标准)、IDEA(国际数据加密算法)等.对于传统加密技术来说，其主要是对文本信息加密，其操作简单，但对数字图像加密需对图像做预处理，因此图像加密速度慢.2)数字图像像素置乱的加密技术.对于图像像素置乱加密技术来说，该方法所涉及的变化为线性变换，操作简单，容易实现，运算速度快，但经过几次迭代后，明文信息就可以被完全显示出来，所以该方法抗攻击性弱，安全性差.3)图像秘密分割及共享的加密技术.此技术算法简单、直观、安全性好、具有较好的抗干扰性，但图像数据量易发生膨胀，不利于在网络中传输.

因此，迫切需要设计一种安全程度高、操作简单、运算速度快、利于图像在网络中传输的加密方案.混沌是一种非线性动力学系统，混沌现象表现为确定性系统中的内在随机特性.由于混沌系统的初值敏感性及长期不可预测性，因此混沌系统特别适合应用于现代化的图像保密通信技术中.鉴于混沌系统的内在随机性，本文利用Henon映射及细胞神经网络超混沌系统所产生的混沌信号对图像加密，增强了加密序列的安全性.

1 Henon映射混沌及细胞神经网络混沌系统

1.1 Henon映射混沌系统

混沌现象是自然界中普遍存在的一种复杂现象，其主要表现为不规则、不连续及不稳定特性.Lorenz在1963年发现了第一个混沌系统,自此之后各式各样的新混沌系统也不断被人们所发现.法国天文学家和数学家Michel Henon在1976年对一种二维函数进行研究时发现了一种复杂系统，定义为Henon混沌系统.

Michel Henon从球状星团以及洛伦兹吸引子中得到启发,对一种形式简单的二维函数过程进行研究,发现它是具有一些特殊性质的复杂系统，该系统即为Henon混沌系统.此后国内外许多学者不断对Henon混沌系统进行数值模拟以及仿真研究，最终将Henon混沌系统从二维系统扩展到高维，给出了广义Henon混沌系统.基于前人研究，Richter在2002年定义了无限维的广义Henon混沌系统，其表示形式如下[1]：

(1)

式中：w表示维数，当w>2时，该系统处于超混沌状态；i=2,3,…,w；a和b为控制参数，实验证明当a=1.76,b=0.1时系统处于超混沌状态.当w=2时，该系统即为著名的Henon映射[2].目前具有内在随机特性的广义Henon映射已经成为人们在图像加密过程中经常用到的混沌映射之一.基于此,本文研究5维Henon映射的超混沌现象，用于图像加密技术的应用中，即w=5，其表示形式为

(2)

当a=1.76，b=0.1，初始值xj(1)=1,j=1,2,…,5时所产生的混沌轨迹如图1所示.

1.2 细胞神经网络混沌系统

Chua在1988年首次提出细胞神经网络(Cellular Neural Network，简称CNN)概念，它是一种局部互连的神经网络系统[3].系统具有极其复杂的动力学行为，能够实时、高速、并行处理信号，该系统已被广泛应用于各种图像处理、模式识别等领域.实验证明这种复杂系统在相当大参数范围内能够产生混沌现象，因此利用该系统所产生的混沌序列对图像加密很大程度增强图像的安全性.

图1 Henon系统混沌轨迹图

(3)

(4)

由式(3)和式(4)推得5阶的全互连CNN动态模型为

(5)

其中参数选取为

(6)

把以上参数代入式(5)，可得CNN微分方程组为式(7)：

(7)

利用四阶Runge-Kutta算法求解上述式(7)，产生的混沌吸引子如图2所示.格里波基在1983年已经证明只要最大Lyapunov指数大于零，就可以肯定混沌的存在.存在正的Lyapunov指数个数大于等于2时，就说明系统处于超混沌状态.本文选择Henon所产生序列的第100个作为CNN系统初始条件时，计算每个状态下Lyapunov指数λ1,λ2,λ3,λ4,λ5，图3为该系统Lyapunov指数谱系图，计算得到Lyapunov指数分别为λ1=4.958 3,λ2=2.487 7,λ3=-6.501 0,λ4=-105.683 2,λ5=-2.958 0，从而可知其中有2个正的Lyapunov指数大于0，因此可以证明该5阶细胞神经网络处于超混沌系统.

图2 CNN超混沌系统混沌吸引子

图3 系统Lyapunov指数谱系图

2 图像加密算法

每一幅灰度图像对应着M行N列的数字矩阵，矩阵中每一个点对应着图像的一个像素值，像素值为[0,255]之间的整数，其值即为图像灰度值.假设通讯双方共同持有5维Henon映射和5维细胞神经网络系统，并且双方共同享有密钥集，即5维Henon映射密钥集key1={a,b,(xi,i=1,…,5)}以及5维细胞神经网络系统中如式(6)中的60个参数密钥.

2.1 图像加密算法过程

Step1 发送方利用广义Henon映射生成序列①：x1(k),x2(k),x3(k),x4(k),x5(k)，其中k可自行设定.

Step2 发送方利用上面生成的序列①作为细胞神经网络的初始条件，利用细胞神经网络系统(5)生成序列②：y1(k1),y2(k1),y3(k1),y4(k1),y5(k1)，其中k1可根据图像情况具体设定.

Step3 重复步骤(2)k次，将每次得到的数②扩展生成序列③：z1(k*k1),z2(k*k1),z3(k*k1),z4(k*k1),z5(k*k1)，且使得k*k1=M*N,最后将③重新排列，排成图像大小M行N列矩阵④：t1(M*N),t2(M*N),t3(M*N),t4(M*N),t5(M*N).

Step4 分别取常数k2=9,k3=99,k4=999,k5=999 9,k6=999 99，对矩阵④做如下处理，得到序列⑤：l1(M*N),l2(M*N),l3(M*N),l4(M*N),l5(M*N),

l1=mod(round(t1*k2),256),

l2=mod(round(t2*k3),256),

l3=mod(round(t3*k4),256),

l4=mod(round(t4*k5),256),

l5=mod(round(t5*k6),256).

Step5 发送方利用生成的序列⑤与l(i,j)=0按如下方式产生加密序列l(i,j)：

l=mod(l+l1+l2+l3+l4+l5,256).

Step6 对原始图像加密，令Yimage=mod(l+Ximage,256)，形成加密图像.

Step7 接收方收到密文Zimage，解密即加密的逆过程，接收方根据上述步骤解密得到明文图像Ximage.

3 实验仿真及结果安全性分析

3.1 实验仿真

本文选取400*400大小的灰度图像[7-9]，按照以上加密算法对该图像加密，实验仿真结果如图4所示，其中(a)图为原始图像，(b)图为加密图像，(c)图为解密图像.可见该加密方案能够完全无损恢复出加密图像.

图4 模拟实验结果

3.2 结果安全性分析

3.2.1 密文熵分析

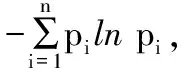
3.2.2 像素相关性分析

每幅图像之间存在某种相关关系，也正是由于这种相关性，图像才可以完全清晰呈现在人们面前，若相邻像素之间不存在某种相关性，图像像素位置杂乱无章，就不能识别图像.为验证原始图像和加密图像各像素间的相关性，本文从水平方向、竖直方向和对角线方向出发，分别做图像相邻像素散点图.图5(a)显示了原始图像水平方向相邻像素灰度值的散点图，图5(b)表示加密图像在水平方向上相邻像素散点图，表明原始图像水平方向各像素间存在较强的线性关系，而加密图像中散点在整个空间均匀分布，各像素间没有明显的线性关系，同样在竖直方向和对角线方向可得到类似结论，本文不再赘述.

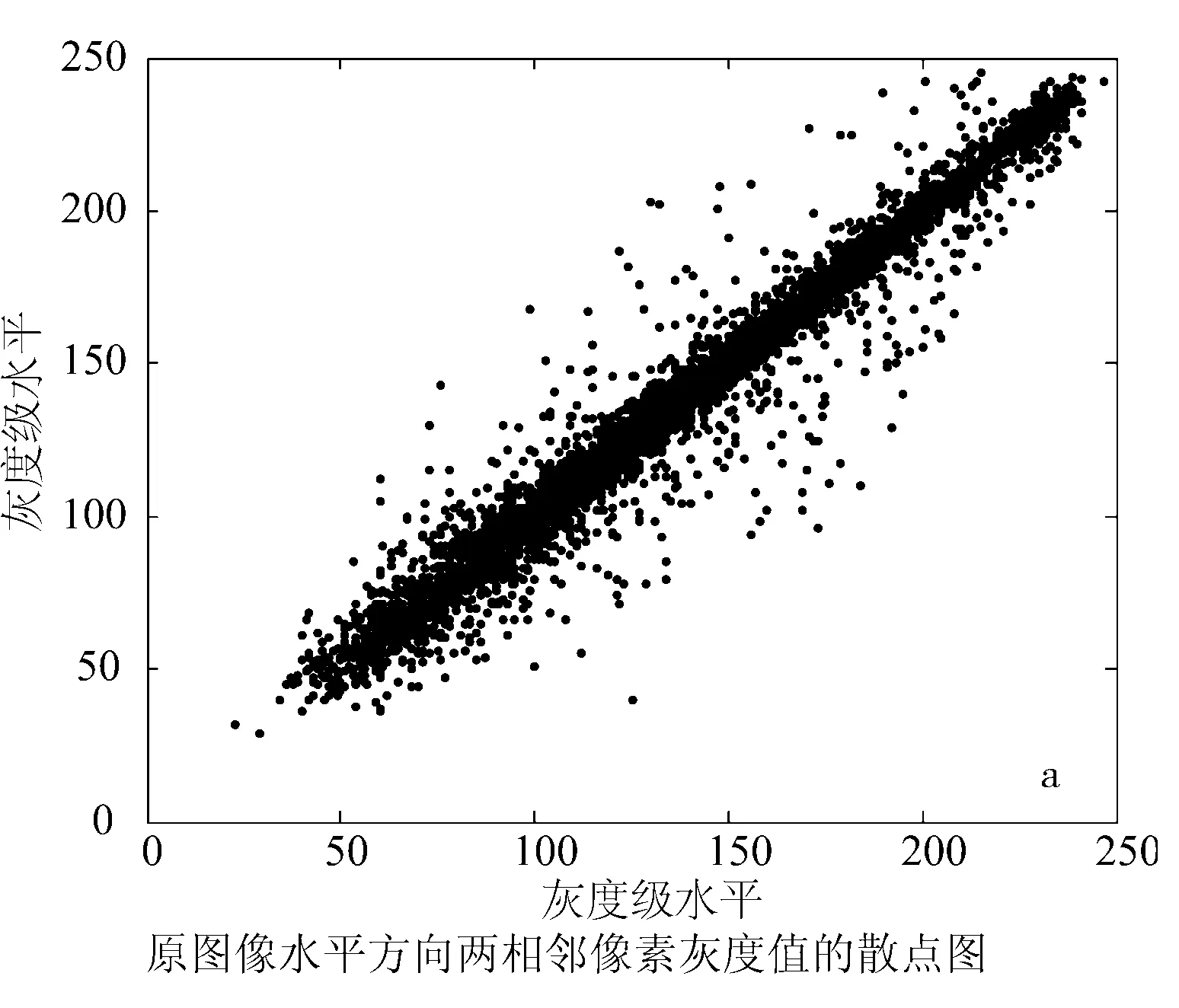
图5 图像水平方向像素之间相关关系

为了定量说明原始图像和加密图像像素之间的相关性，本文计算相邻像素的相关系数，随机选取10 000个相邻像素点作为训练样本，相关系数计算见式(8)，实验结果见表1，显示原始图像和加密图像在不同方向上相邻像素的相关系数.

(8)

表1中数据验证：加密图像无论是水平方向、垂直方向还是对角线方向上相邻像素之间相关系数较大，说明存在较强的线性关系.而加密图像相关系数趋近于0，图像像素之间相关性荡然无存.因此可以证明加密图像中已经不存在原始图像的统计特性，加密效果好.

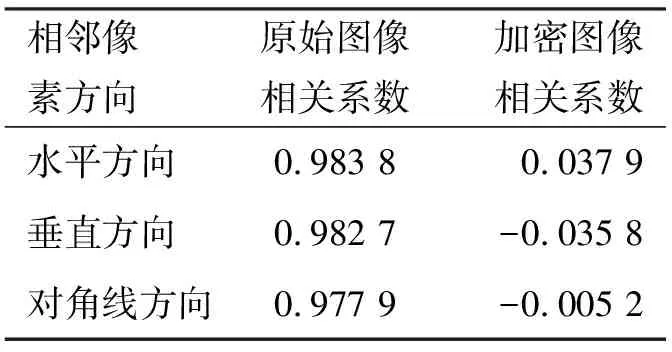
表1 原始和加密图像相邻像素之间相关系数

3.2.3 图像直方图分析

图6分别给出了原始图像直方图和加密图像直方图，通过比较可以看出，在原始图像中，直方图错落有致，明显看出像素之间存在某种关系.加密后图像直方图分布发生巨大变化，直方图分布均匀，说明原始图像的统计特性已不存在，因此加密图像有较强的抵抗能力.

图6 图像像素直方图

3.2.4 密钥空间及敏感性分析

算法对系统参数依赖程度较大，只要参数有微小变化，接受者就不能完全无误解密出加密图像，也验证算法的抗攻击能力较强.实验仿真结果表明，本文算法对Henon映射中的7个参数，细胞神经网络系统中的60个参数的敏感程度都非常高，均达到10-16，也就是说图像加密过程中使用的加密密钥中有10-16的微小变化，攻击者就不能解密出原始图像，此时攻击将是徒劳的.图7分别给出了两个混沌系统的某一个参数发生变化时解密出来的图像.图7(a)为原始图像；图7(b)表示Henon系统初始条件x(1)变化为x(1)=1+10-16时的解密图像；图7(c)表示细胞神经网络系统系数a4变化为a4=2+10-16时的解密图像，本文算法密钥空间也是相当大的，其中使用的密钥总共67个，则密钥空间中个数将达到(1016)67.

图7 图像对密钥敏感性测试

另外算法中涉及的一些常数也设计为密钥的话，密钥空间将进一步扩大，可见本文算法对攻击者来说抵抗能力较强.

5 结论

基于复杂的网络环境，本文设计了一种更有利于图像在网络中传输的图像加密方案即基于广义Henon映射、5阶CNN超混沌系统的加密方案.基于产生的超混沌序列对原始图像做变换得到密文图像，文中最后做了模拟仿真实验并对结果进行了安全性分析，得出以下结论：1)信息熵作为随机性评价的统计指标来衡量本文加密方案，计算加密图像信息熵为7.998 8，接近理想水平信息熵8，加密效果好.2)本文用像素之间相关系数作为衡量图像统计特性的统计指标，验证表明原始图像相关系数接近1，加密图像相关系数接近0，证明加密图像不存在原始图像的统计特性.3)混沌系统对初始值的敏感特性以及密钥空间巨大使得加密图像对于反攻者的抵抗能力较强.因此基于5阶广义Henon映射以及5阶细胞神经网络超混沌系统的图像加密方案加密效果好.