基于BP神经网络的交流输电线路可听噪声预测模型

唐 波，彭友仙，陈 彬，瞿子航，李 昱

(三峡大学 电气与新能源学院, 湖北 宜昌 443002 )

0 引言

输电线路产生的可听噪声已经干扰到人们的生活，尤其是特高压输电线路产生的噪声[1]，与相同声压级的环境噪声相比更令人烦躁和难以忍受.在特高压交流输电线路的设计过程中，可听噪声的影响越来越显著.文献[2]表明，可听噪声是选择导线结构、影响造价成本、确定输送电压的主要因素.在线路设计前，对输电线路可听噪声的大小进行预测可以帮助线路设计人员选择合理的导线型式.

为了帮助线路设计人员选择合理的导线型式，许多研究人员通过试验段或电晕笼得到了可听噪声的各种预测模型，文献[3]和文献[4]对各种模型作了详细的介绍，如直接预测法的AEP(American Electric Power)计算公式模型、间接预测法的GE(General Electric)计算公式模型等.然而，由于适用条件的约束和预测误差偏大等问题，各类预测模型在实际线路设计过程中的应用都受到一定程度的限制.因此，开展具有通用性强、预测准确度高的可听噪声预测模型的研究将具有实际的应用价值.

本文应用BP(Back Propagation)神经网络[5]对可听噪声值进行预测，实现可听噪声值与其影响因素之间复杂关系的数学拟合，从而解决传统预测模型在工程应用中存在的局限性或预测精度不高的问题.

1 可听噪声影响指标的确定

1.1 可听噪声

输电线路可听噪声是指电力线路发生电晕放电时，产生的人能够听见的噪声，它是衡量输电线路电磁环境质量的重要指标之一.对于交流输电线路，通常雨天的可听噪声会比晴天大15～20 dB(A)，因此，按照国际惯例，在特高压输电线路的设计过程中，采用雨天时的L50(即雨天时的50%值)作为可听噪声限值，这是对最严重情况下噪声的限制，在其他情况下，噪声都将小很多[4].因此，本文以L50值作为可听噪声的特征指标.

1.2 影响指标的确定

国际上使用的噪声预测模型的通用表达式为[6]：

SL=f(g,N,d,D),

(1)

式中：SL为输电线路产生的统计噪声L50，dB(A)；g为分裂导线的表面电位梯度，kV/cm；N为导线分裂数目；d为子导线直径，cm；D为测量点至导线的径向距离，m.

由式(1)可见，输电线路统计噪声y=L50是线路参数X=(g,N,d,D)的函数，可听噪声的预测问题可以转化为根据给定的测量噪声样本，寻求最优函数f:x→y.因此，本文主要以线路参数X=(g,N,d,D)作为可听噪声的影响指标，通过BP神经网络对其进行训练学习，逼近数据中隐含的非线性机制f，使f能够对未知输出噪声做出尽可能准确的预测.

2 常用可听噪声计算模型的分析

2.1 AEP公式

AEP计算公式是直接预测法中的一种预测模型，计算公式为[7]：

SLAEP=108lgg+10lgn+

75.9lg(d/2.54)1.35-94.5,

(2)

式中：g为中相的平均最大表面电位梯度，n为导线分裂数目，d为子导线直径.

该公式可直接计算预测输电线路的总噪声，但仅限于三相运行线路，且仅适用于500～800 kV运行线路，具有一定的局限性.

2.2 GE公式

GE计算公式是间接预测法中的一种预测模型，单相可听噪声的计算公式为[8-9]：

Li50=Li5-ΔL,

(3)

式中：Li5为雨天时5%的噪声值，其计算见式(4)；ΔL为修正量，其计算见式(5).

Li5=-665/g+20lgn+44lgd-

10lgD-0.02D+L0+k1+k2,

(4)

式中：g为分裂导线的平均最大表面电位梯度；D为测量点至导线的径向距离；L0的取值为：当n<3时，取为75.2 dB(A)；当n≥3时，取为67.9 dB(A).k1的取值为7.5(n=1时)或2.6(n=2时)或0(n≥3时)；k2的取值为0(n<3时)或按k2=22.9(n-1)d/B(n≥3时)计算，其中B为相导线的直径，cm.

(5)

式(5)中，gc的计算如下：

(6)

该公式可计算预测单相线路的可听噪声值，对超、特高压线路均适用，但其计算误差通常偏大，应用于实际会造成较为严重的环境影响问题.

3 BP神经网络可听噪声预测模型

3.1 BP神经网络结构

BP神经网络可以具有三层或三层以上的网络层次结构，BP网络能学习和存贮大量的输入、输出模式映射关系，无须事前揭示描述这种映射关系的数学方程.它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小.三层BP神经网络模型拓扑结构包括输入层、隐含层(隐含层可以是一层或多层)和输出层，每个神经元用一个节点来表示.BP网络的基本结构如图1所示.

图1 BP神经网络结构图

3.2 网络的输入和输出变量

可听噪声的预测模型根据其建模数据的特征可以分为直接预测模型和间接预测模型.直接预测模型只适用于特定的线路结构类型和特定的电压等级；间接预测模型主要建立单相线路的噪声预测模型，再利用式(2)计算线路产生的总噪声，适用于各种线路结构类型和各类电压等级.

(7)

式中：SLall为多相输电线路产生的总噪声，dB(A)；Li为每相线路产生的噪声，dB(A)；p为相数.

因此，采用间接预测法进行建模，网络的输入变量则记为X=(gsp,N,d,Dsp)，其中：gsp为单相分裂导线平均最大电位梯度值，Dsp为单相导线到测量点的径向距离.

综上所述，输入变量单相输电线路的线路参数，那么相应地输出变量即为单相输电线路产生的噪声.

3.3 BP神经网络算法

BP算法可以从输入层经过隐含层逐层处理后传至输出层，也可以在输出层得不到预期输出时反向传播.反向传播过程中，误差信号沿着连接路径返回，通过修改各层神经元之间的连接权值，从而使得误差信号最小，输出结果最优.

假设某网络有N层，如果采用单输出神经模型，那么第N层仅含有输出节点，第一层为输入节点.设有M个标准样本：{x1(p)，x2(p)，xn(p)；xi(p)|p=1,2,…,M}.第N层网络输出为z(p).隐含层与输出层通过Sigmoid函数输出，Sigmoid函数反映了神经元的饱和特性，其表达式为

(8)

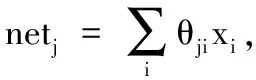
(9)

式中，θji(i=1,2,…,n；j=1,2,…,m)为输入层与隐含层节点的连接权值.

下面，分两种情况讨论：

1)若节点j为输出节点，则yj=z，

(10)

2)若节点j为隐含层节点，则有

(11)

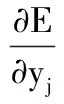
在(m+1)层第l个节点：

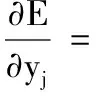
(12)

由式(11)和式(12)可以得到：

(13)

根据上面的理论和推导，则可概括出BP算法的步骤如下：

1)选取初始值、阈值；

2)计算每层各节点j的yj，netj和z的值；

3)从N到第二层，对每层节点，利用式(10)和式(8)反向计算δj；

4)修正权值

(14)

5)重复步骤2)至4)，直至满足要求.

4 具体算例

4.1 数据收集

通过搜集国外交流输电线路可听噪声测量的数据[4]，整理出可供间接法使用的可听噪声样本{Xn,Ln}，一共57个样本数据，包含3种线路结构(如图2所示)的数据，选取包含3种线路结构的任意6个样本作为预测集，用剩下的51个样本作为训练集.数据样本如表1(由于数据量大，只列举部分)和表2所示.

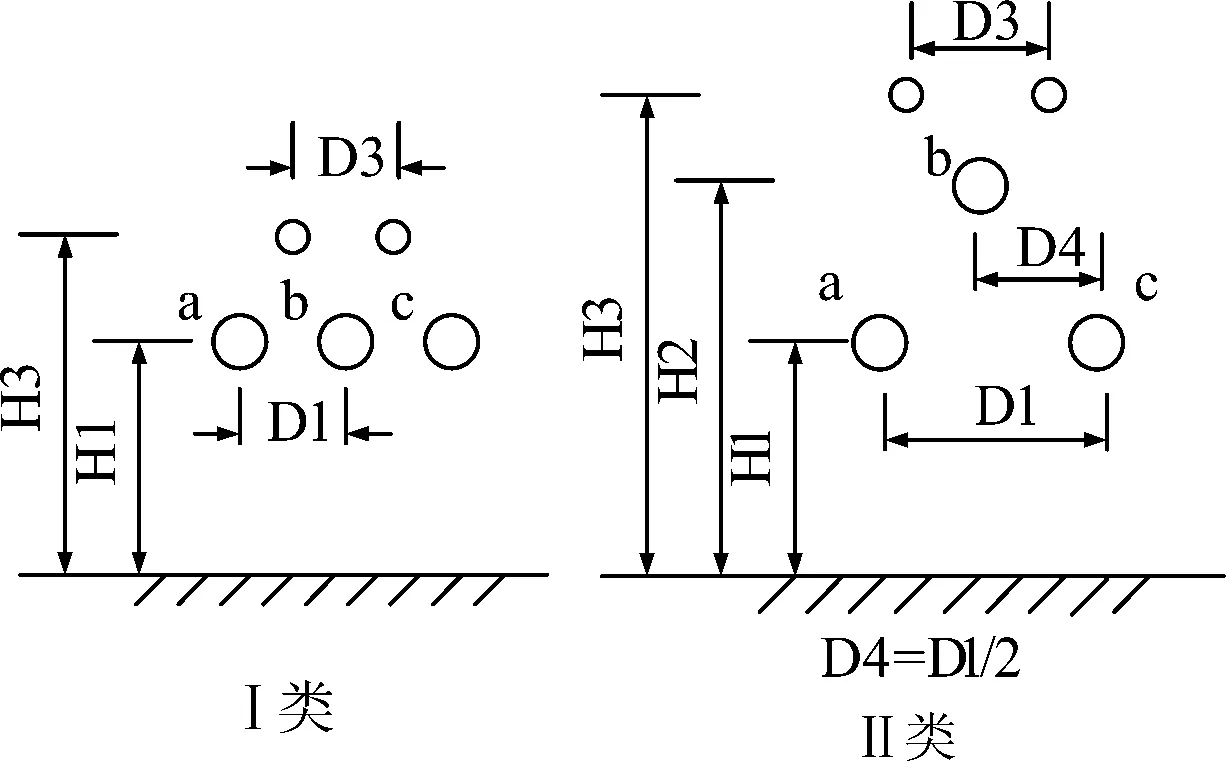
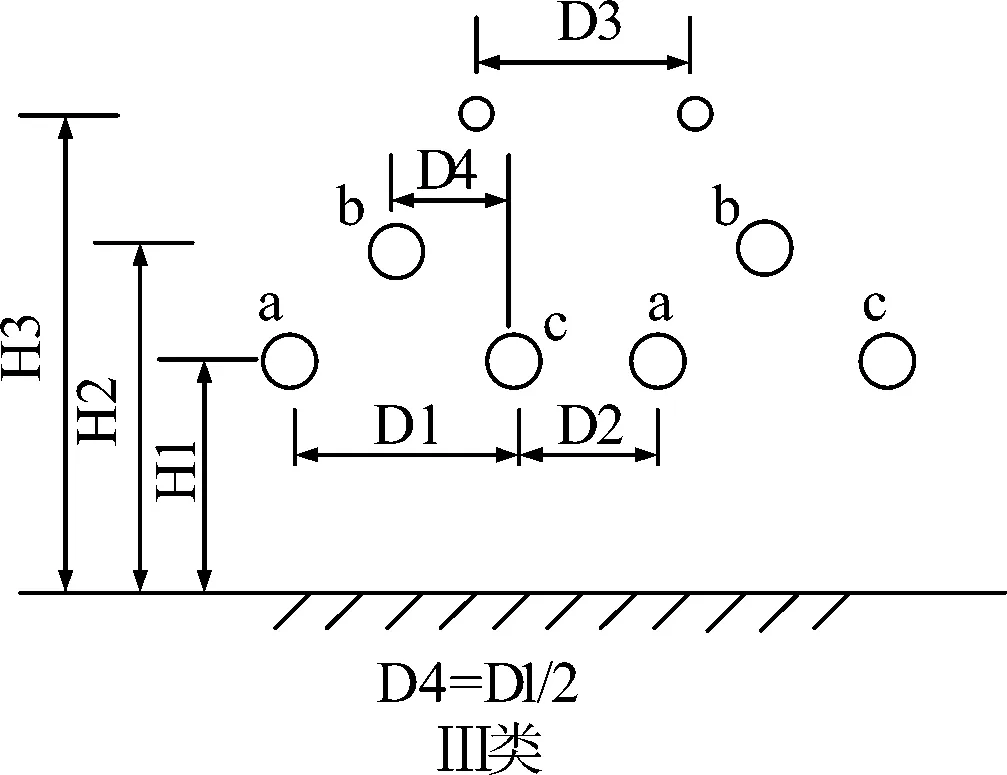
图2 线路结构类型

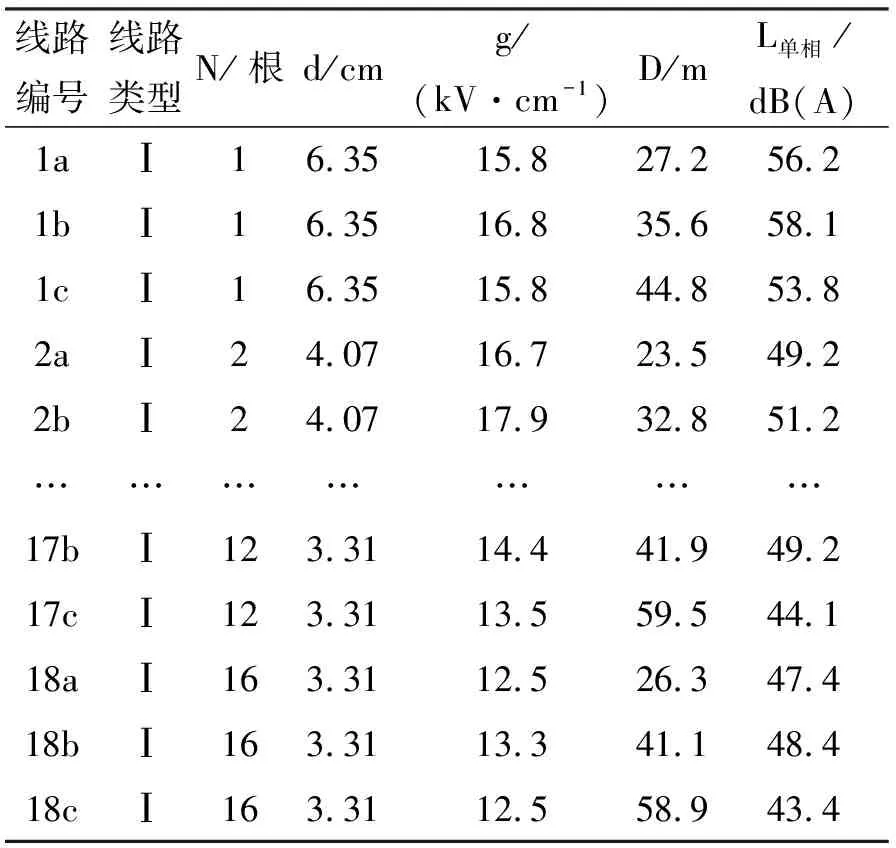
线路编号线路类型N/根d/cmg/(kV·cm-1)D/mL单相/dB(A)1aⅠ16.3515.827.256.21bⅠ16.3516.835.658.11cⅠ16.3515.844.853.82aⅠ24.0716.723.549.22bⅠ24.0717.932.851.2…………………17bⅠ123.3114.441.949.217cⅠ123.3113.559.544.118aⅠ163.3112.526.347.418bⅠ163.3113.341.148.418cⅠ163.3112.558.943.4

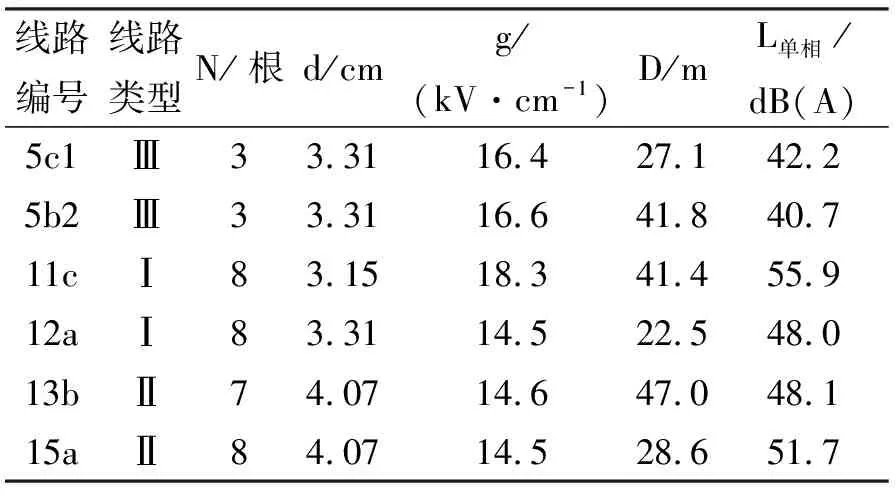
表2 预测集数据样本

4.2 数据的预处理

由于输入和输出变量在数值上的变化相差较大且量纲不同，故不能直接用于网络训练，否则会严重影响网络学习的速度及精度等.因此，在训练学习前，对样本数据的预处理是十分重要的一个环节.采用常用的归一化函数premnmx函数对样本数据进行归一化处理，归一化后的训练样本数据均在[-1,1]的范围内.

4.3 BP神经网络训练

在MATLAB环境中进行神经网络的训练学习，设定显示间隔次数为50；最大循环次数为100 000；目标误差为10-4；初始学习速率为0.01，将预处理后的数据输入网络进行训练，经过100 000次训练后结束.

绘制网络训练的拟合曲线图如图3所示.

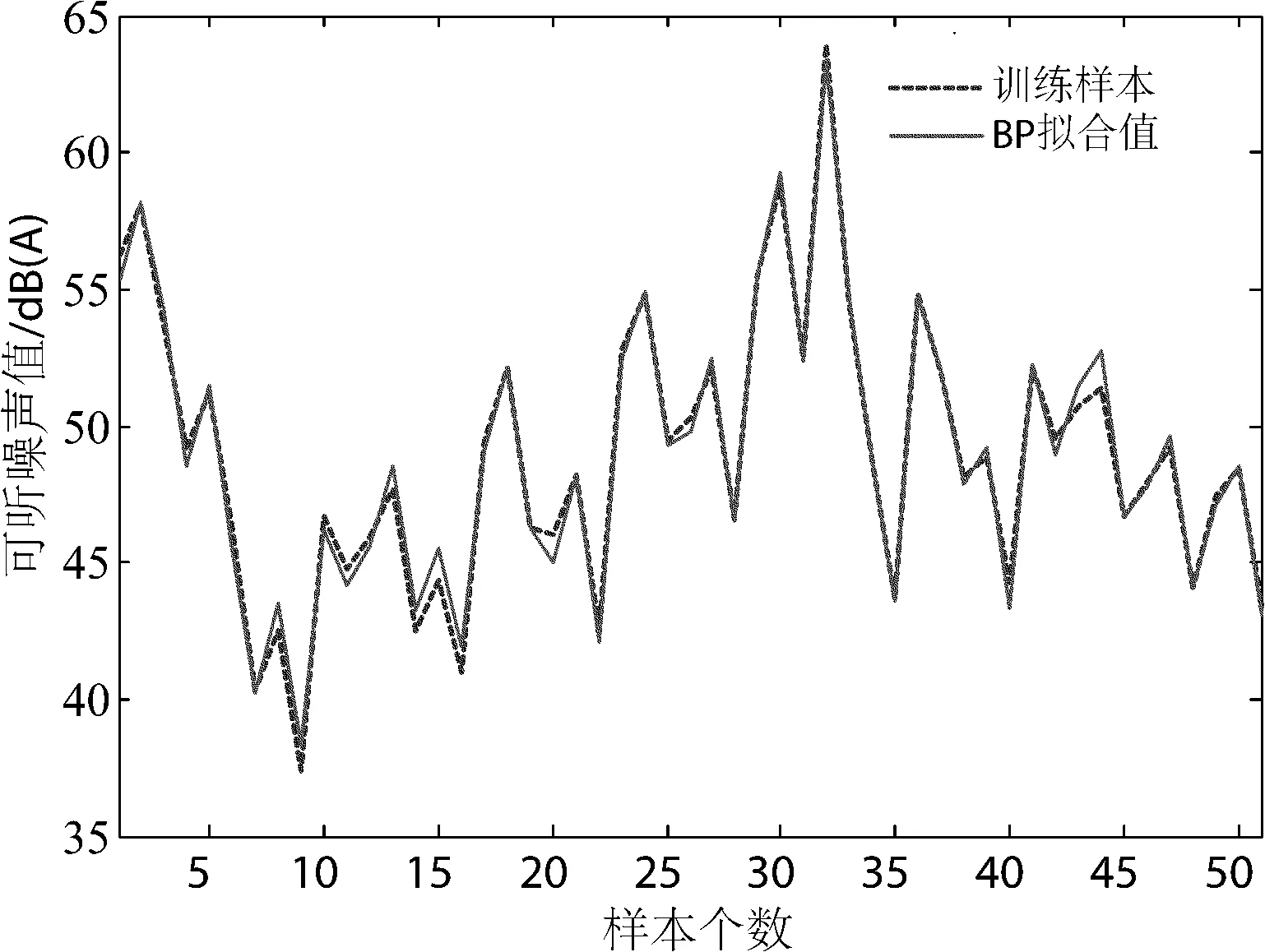
图3 BP神经网络训练拟合曲线

由图3可以看出，应用BP神经网络进行训练的拟合效果很好，训练样本的拟合值与实际值曲线十分接近.利用MATLAB计算预测结果的残差，结果表明，预测残差值基本上在[-1,1]范围内波动.由此可见，该网络模型拟合精度很高.

4.4 预测结果及分析

用训练好的网络对预测集线路的可听噪声进行预测.在MATLAB环境下，将预测集样本线路参数用tramnmx函数进行归一化处理后，输入网络进行预测，得到归一化的预测结果后，通过postmnmx函数进行反归一化，最后结果及误差如表3所示.

表3 预测集线路的可听噪声预测结果

分析表3中的数据可知：

1)预测的6条线路中，绝对误差绝对值最大为1.135 7 dB，根据实地测量经验，预测值满足可听噪声预测精度要求；2)该网络模型可应用于预测不同类型线路的可听噪声，结果准确度几乎不受线路结构影响；3)预测结果与实际值的相对误差基本在2%以内，与实际值的贴近度相当可观.

4.5 与GE算法的比较

选取Ⅰ类线路结构的14号、Ⅱ类线路结构的13号以及Ⅲ类线路结构的5号线路进行BP神经网络预测，并利用式(2)计算出线路总的可听噪声值，同时采用GE公式进行预测计算，并计算出二者与实际值间的平均绝对误差，结果如表4所示.

表4 BP预测与GE公式计算结果对比

由表4数据可知，BP神经网络预测模型的平均绝对误差绝对值比GE公式计算结果的平均绝对误差小1.641 4 dB(A).

综上所述，基于BP神经网络建立模型对可听噪声进行预测，准确度高，适用范围广，可用于实际.

5 结论

1)利用BP神经网络预测模型对预测集进行可听噪声值的预测，绝对误差绝对值最大仅为1.135 7 dB(A)，且满足可听噪声预测精度要求.

2)采用间接预测法，基于BP神经网络算法建立交流输电线路可听噪声预测模型，预测结果相对误差仅在2%以内，且适用于不同线路结构的输电线路.

3)模型预测的是单相线路的可听噪声，对于多相线路，采用式(2)计算线路的总噪声即可.BP神经网络预测模型预测的平均绝对误差比GE公式的平均绝对误差小1.641 4 dB(A)，表明BP神经网络预测模型具有更高的预测精度.