基于分频段ABAP谱减法的鸟叫声分类研究
2015-08-08张妍琰刘建芳郭力争
张妍琰,刘建芳,郭力争
(1.河南城建学院 计算机科学与工程学院,河南 平顶山 467036;2.平顶山学院 软件学院,河南 平顶山 467000)
0 引言
鸟类是自然生物的重要成员之一,在物种演化的漫长过程中,大多鸟类都形成了具有自身特异性的鸣叫声.通过对鸟叫声的研究,有利于提高对鸟类资源、种类、数量、生存区域统计调查的准确性、真实性和可靠性,同时可将其作为分析自然声音的组成结构和动物行为的典型样例.
自然环境中的鸟叫声通常伴有杂音,为了去除噪声,得到较为纯净的声音信号,必须借助于各种声音增强算法.谱减法[1]是声音增强算法中重要的非参数方法,谱减法以其原理简单、运算量小、性能稳定而受到最为广泛的关注和研究.传统谱减法[2-3]采用的周期图估计并非一致估计,方差很大,并造成“音乐噪声”,影响谱减后声音分类效果,尤其是鸟类声音的分类,因为鸟叫声中夹杂的自然环境噪声组成复杂、种类繁多,且在频域上分布较广.为了抑制“音乐噪声”,降低方差,Hendriks等人通过搜索功率谱的最长平稳段,进行周期图平滑,进而减小周期图估计的方差[4].但是因果系统并不能得到理论上的最长平稳段,该搜索过程还需要较大的数据存储量和计算量,并且这种周期图平滑利用的只是时域的平稳性,却没有考虑功率谱频域上的结构特征,无法应对复杂的自然声音.Ephraim等人提出的引导决策(Decision-Directed, DD)算法能够较好地估计高信噪比情况下的功率谱[5].但是当信噪比较低时,DD算法会低估先验信噪比,造成跟踪延迟和声音失真的问题[6].Gustafsson等人采用Bartlett平均周期图(Bartlett Averaging Periodogram, BAP)方法先将信号分段估计,然后平均各个分段结果[7],以减小估计方差,平滑功率谱图.但是该方法造成严重的能量泄露,影响算法性能.Welch方法引进重叠加窗改进了Bartlett法,虽然能在一定程度上抑制能量泄露,但是窗函数的选择对估计效果影响较大,需事先针对不同信号和不同的处理目的选择合适的窗函数.实际上,噪声功率谱的结构特征变化复杂,既可能是平坦的连续谱,如白噪声谱;也包括离散的线谱,如正弦信号等周期信号的功率谱;更普遍的是既包括连续谱又包括非连续谱的复杂谱.对于连续谱噪声,应采用频率分辨率较低的功率谱估计以减小方差,从而减少“音乐噪声’;而对非连续谱噪声,则应该采用频率分辨率较高的功率谱计以降低噪声谱能量泄露,减少声音失真.因此无论哪种功率谱估计方法,都难以在方差和频率分辨率之间取得良好的折中.
针对上述问题,本文提出了基于噪声谱结构特征的自适应Bartlett平均周期图(Adaptive Bartlett Averaging Periodogram, ABAP)方法,根据噪声谱的结构特征对周期图进行自适应平滑.真实环境中的噪声对整个声音信号整个频谱的影响并不均匀[8],因此本文将ABAP应用于分频段谱减法(Multi-band Spectral Subtraction,MSS)[9],对自然环境的鸟叫声进行降噪处理,以减少音乐噪声和声音失真.传统的Mel频率倒谱系数(Mel Frequency Cepstrum Coefficient, MFCC)充分利用人耳听觉感知特性,经常被作为声音特征用于分类识别[10],但是MFCC遇到噪声性能骤降.因此本文将含噪声的鸟叫声信号经过前端改进的降噪处理后,在传统的MFCC基础上加入二维离散余弦变换[11],提取更具有针对性、动态性和鲁棒性的二维Mel频率倒谱系数(Two Dimensional Mel-Frequency Cepstrum Coefficients, TDMFCC)来表征鸟叫声信号,最后结合判决分类器支持向量机(Support Vector Machine, SVM)来对含噪声的鸟叫声进行分类识别.
1 前端降噪
1.1 ABAP法
假设纯净声音为s(n),噪声为d(n),则带噪声音表示为y(n)=s(n)+d(n).去噪的目的就是从复杂的带噪声音y(n)中估计出纯净声音s(n).
YN(k,l)为y(n)第l帧N点快速傅里叶变换(FFT)第k个频带分量,其相应的周期图为[12]
(1)
直接周期图法估计的功率谱方差过大,因此引入Bartlett平均周期图(BAP)法,对信号进行帧内分段估计,然后取平均值.
YM(k,l)是第l帧M点FFT第k个频带分量,其相应的Bartlett平均周期图表示为
(2)
其中:N=LM,L是BAP的平均段数,M是每段的样本点数.通过帧内分段平滑,BAP有效降低功率谱方差.
对较为平稳的声音功率谱,BAP法有良好的效果,能有效弥补直接周期图法功率谱估计存在的方差过大的缺陷.而对于波峰较窄的信号,当在频域上变化较大时,所估计BAP分辨率过低,能量泄露较为严重,不能准确反应声音信号.因此在BAP法的基础上,引入自适应频带结构特性平滑机制,形成自适应Bartlett平均周期图(ABAP)法来进行噪声功率谱估计.分析噪声谱的结构特性,根据频带间连续程度,将其区分为连续谱和非连续谱.判断噪声谱是否频带间连续,如果是,则在谱线之间做平滑;否则,不做平滑.

(3)
其中,权值wi满足:
(4)
引入当前频带与相邻频带的功率谱期望比值,作为判断噪声谱是否连续的依据,即:
(5)
其中,E(PD(k))为噪声功率谱期望.当φ(k,l)越接近1,表示频带k与频带k+i的期望越接近,其谱结构越相似,因此这两频带间可以进行平滑以减少方差.
但是判断每个频带与周围2Kf个频带的结构连续性,所需要的运算量过大,无法满足声音分类实时性的要求.因此,考虑频带k与相邻2Kf+1个频带功率谱均值的比作为判决依据.
(6)
为了防止异常噪声点大值的影响,利用调和平均数来代替功率谱均值的计算.
(7)
其中,实验中为PD(k+i)设置下限值0.5,以排除出现零点时均值过小的误差.
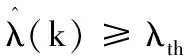
计算判决依据,并确定当前频带的权值wk,
(8)
(9)
(10)
图1中(a)、(b)、(c)分别展示了周期信号加带通白噪声的3种功率谱估计方法的效果.(a)中直接周期图法的帧长N取32 ms的采样点数,(b)中BAP法将N划分为L段,每段的M取4 ms的采样点数.
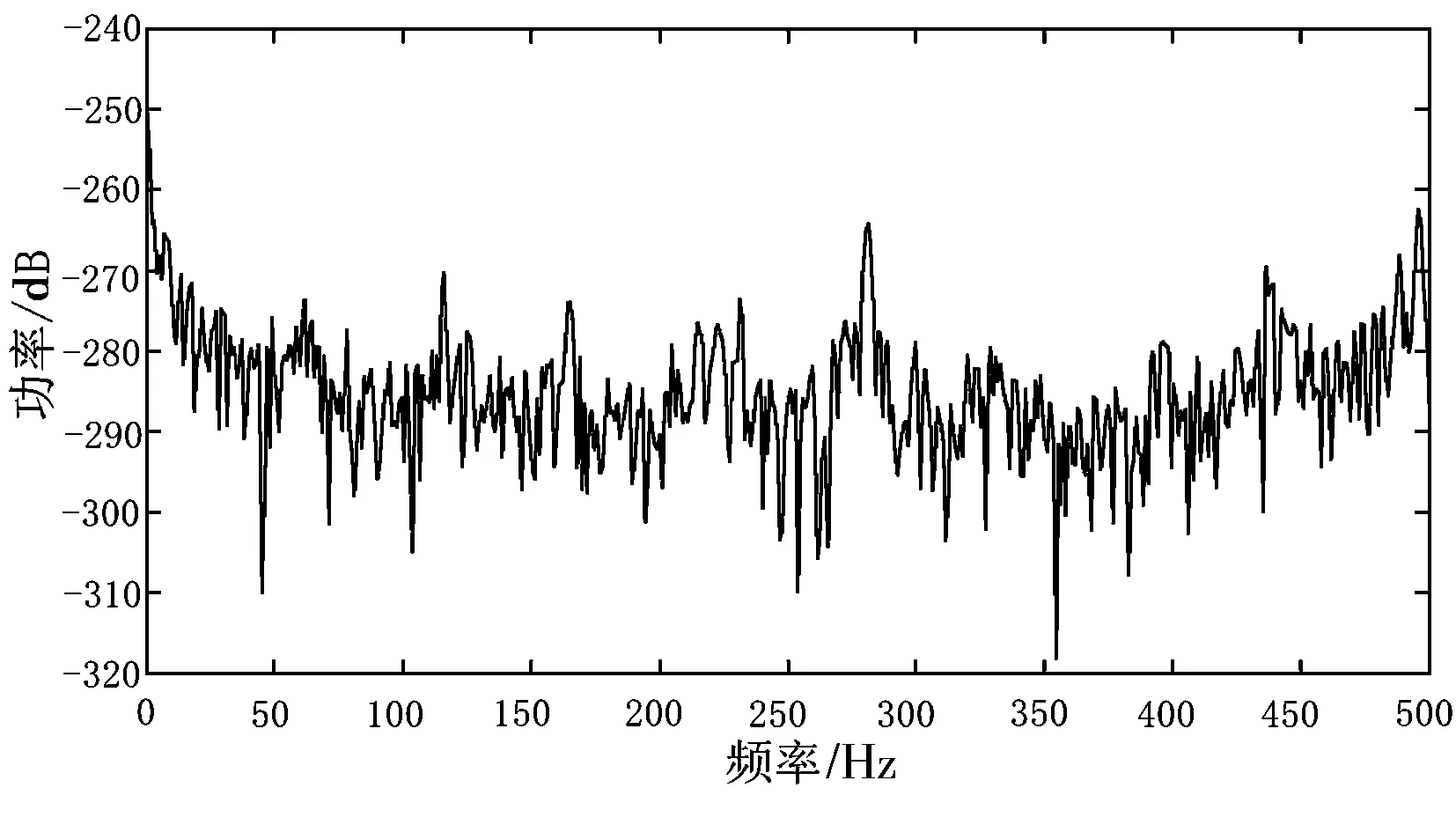
(a)直接周期图法估计结果

(b) BAP法估计结果
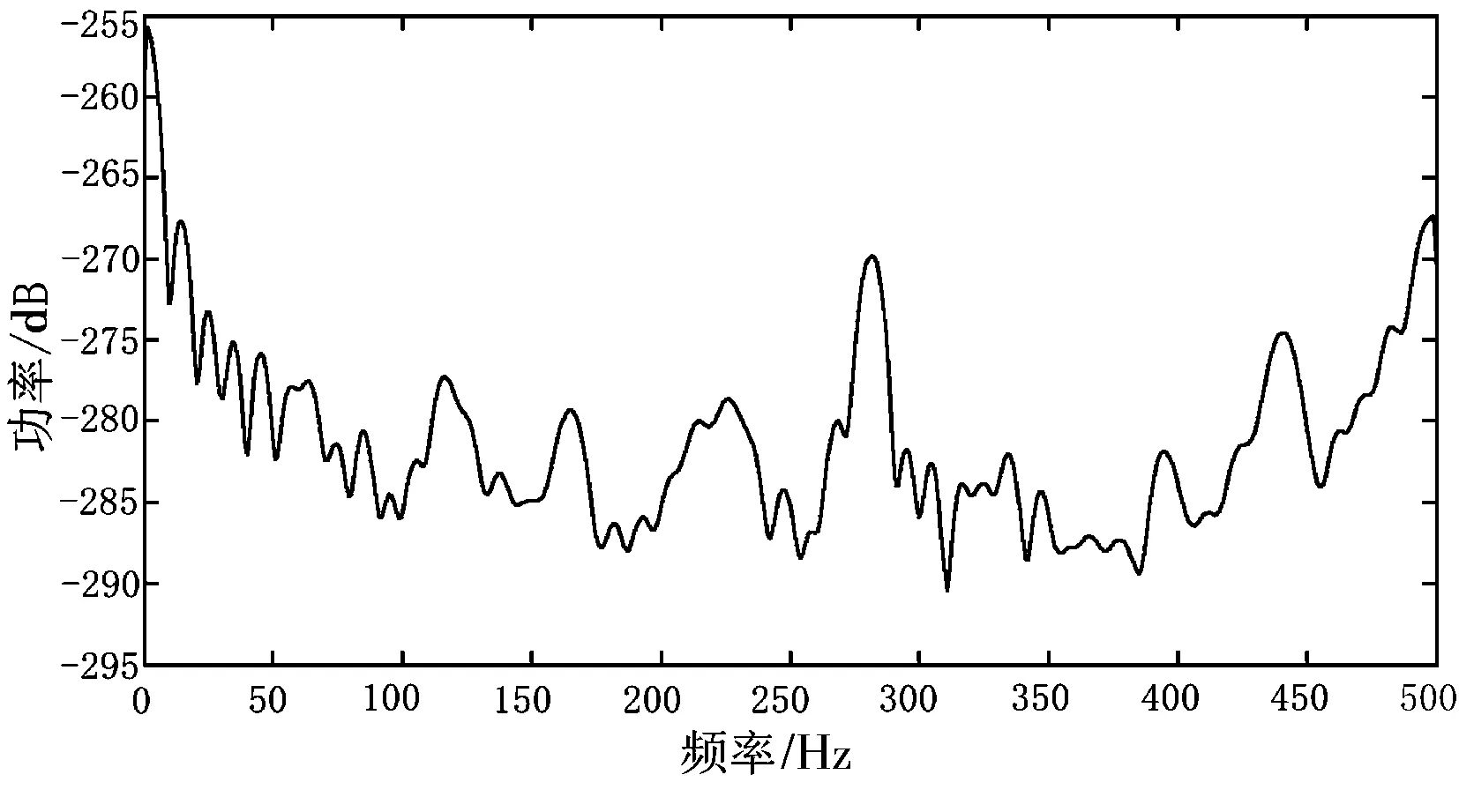
(c)ABAP法估计结果图1 周期信号加带通白噪声的噪声功率谱估计结果Fig.1 Noise power spectrum estimation result of periodic signal with band-pass white noise
由图1的3个对比图可知,(a)中的直接周期图法有较高的分辨率,能量泄露较小,对周期信号具有良好的估计特性,能有效估计窄带噪声,但是对像白噪声这样的宽带噪声,估计的方差很大;(b)中的BAP法虽然方差较小,但能量泄露比较严重,几乎看不到谱线结构,只适用于连续谱估计;(c)中即本文提出的ABAP法,能够根据频带间谱结构的连续性来自适应地平滑周期图,较好地缓解了传统周期图估计中频率分辨率与能量泄露之间的矛盾.
1.2 分频段ABAP谱减法
自然环境的有色背景噪声(风雨声、流水声等)大多是非平稳信号,其均值、功率谱、相关函数等统计量具有随机性,对声音信号功率谱各频段的影响也具有不确定性.因此本文针对不同频率段中噪声谱的影响程度,引入分频段谱减法,并将ABAP的噪声估计方法应用于其中,形成分频段ABAP谱减法来对带噪声音进行降噪,以此提高声音质量.
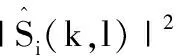
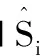
(11)
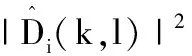
(12)
再根据SNRi(l)和实际实验将αi(l)设定为:
(13)
αi(l)随着信噪比非线性变化,对于信噪比较低的频段αi(l)的取值较大,这使得谱减过程中的噪声干扰被有效抑制.
式(11)中的δi(l)代表用来设定噪声移除特性的补偿因子,根据声音的实际情况和经验设置为:
(14)
其中:fi(l)为第l帧的第i个子频带的最高频率,Fs为声音信号的采样率.
最后,对上述谱减后出现负值的情况进行下限修改,
(15)
Smin(k,l)=Smin-(1-wk)Smax,
(16)
其中:Smin取0.1|Yi(k,l)|2,Smin取0.9Smin.
采用式(15)、(16)主要基于以下两点考虑:第一,对于连续谱,保留残留噪声不变,利用其宽带特性掩蔽“音乐噪声”;第二,与连续谱相比,非连续谱往往具有更大的能量,因此需要对其进行更多抑制,使得残留噪声谱更加平坦,减少音调音出现.
1.3 分频段ABAP谱减法性能测试
为了测试分频段ABAP谱减法对自然环境噪声移除的有效性,将直接周期图估计谱减法、BAP估计谱减法与本文提出的分频段ABAP谱减法进行降噪性能对比实验.对添加10 dB溪流噪声的画眉鸟叫声,分别使用上述3种不同方法进行降噪处理,其效果如图2(a)、(b)、(c)的3种声谱图所示,由图2可知:(1)使用直接周期图估计谱减法对带溪流噪声的画眉鸟叫声降噪后,依然存在大量音乐噪声.(2)使用BAP估计谱减法对画眉鸟叫声降噪后,虽然没有音乐噪声,但是低频段声音被严重抑制,信号能量泄露严重,声音失真较为严重.(3)使用分频段ABAP谱减法降噪后,不但没有残留音乐噪声,而且低频段的声音失真也较少,降噪效果较好.
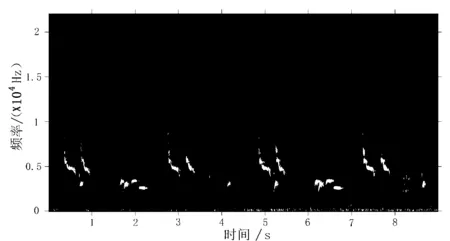
(a)直接周期图估计谱减法降噪后的画眉声谱图
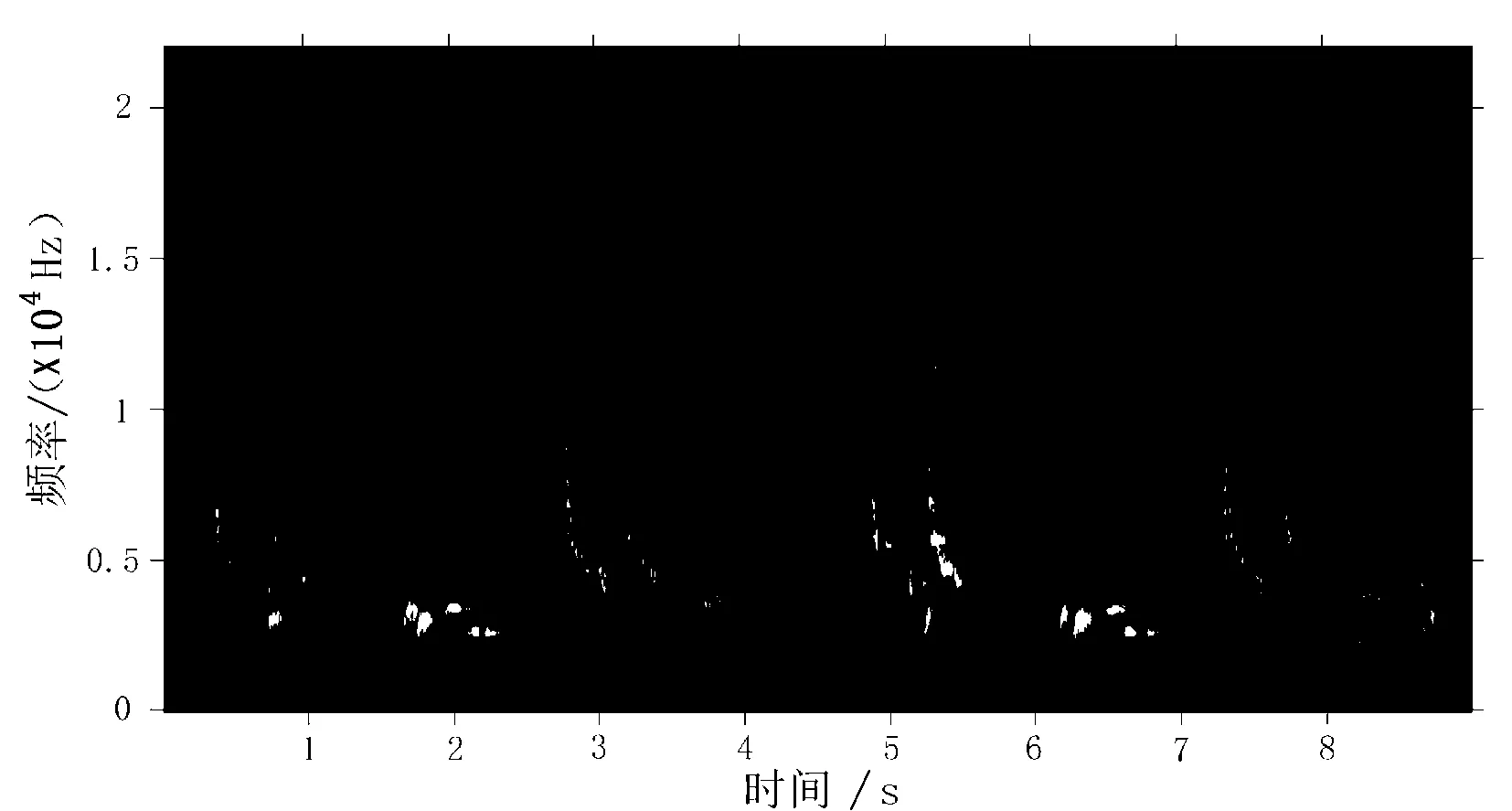
(b)BAP估计谱减法降噪后的画眉声谱图
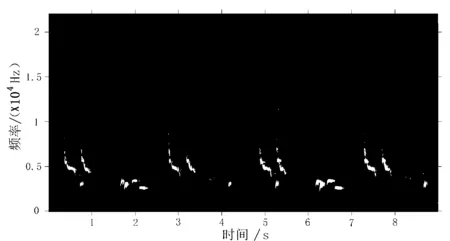
(c)分频段ABAP谱减法降噪后的画眉声谱图
综上说明,本文提出的分频段ABAP谱减法既能解决噪声估计方差太大的问题,减少音乐噪声,又能有效解决因能量泄露而导致的声音失真问题.
2 TDMFCC特征提取
多频段的频谱结构变化包含了声音信号的动态特征,为了更加充分地利用声音信号的动态和静态特征,本文引入二维离散余弦变换[13-14]的Mel频率倒谱系数(Two Dimensional Mel-Frequency Cepstrum Coefficients, TDMFCC).
Mel频率倒谱系数[15-16]是目前广泛使用的声音识别特征,信号的第t帧第q个MFCC系数可以表示为:
(17)
其中:Ei(b)表示通过第t帧第b个Mel滤波器的能量,B是Mel滤波器的总数量.经过二次离散余弦变换(Discrete Cosine Transform, DCT)后的TDMFCC矩阵可以表示为:
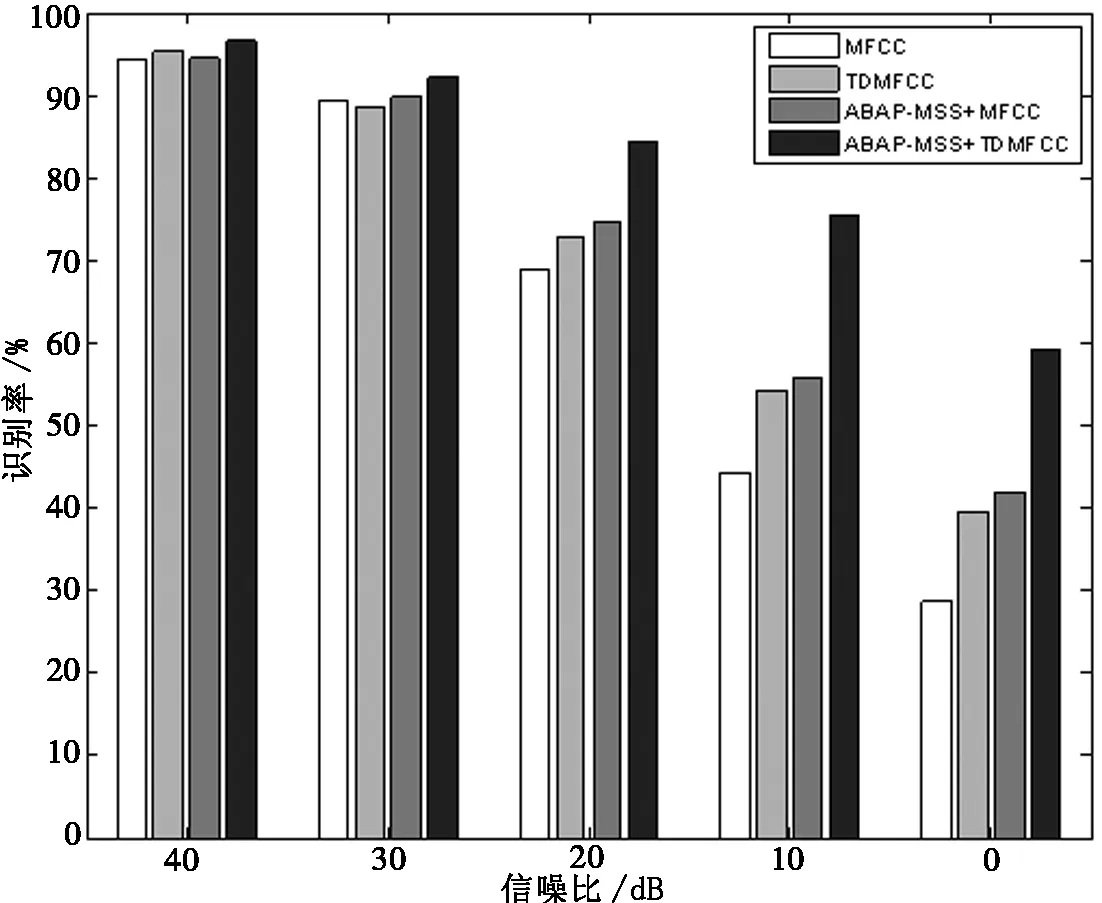
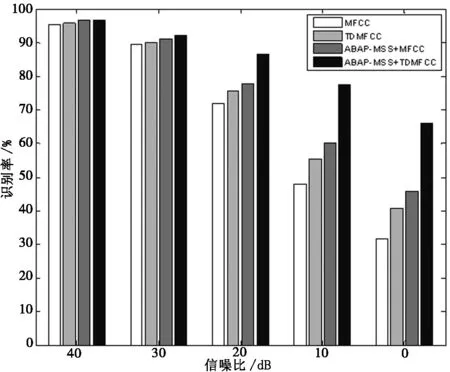
0≤q (18) 其中:n是调制频率的索引,L是声音信号的总帧数. TDMFCC的结构图如图3所示,通过对连续对数频谱序列进行横向二次DCT变换,可以得到包含各序列间频谱变化信息的TDMFCC矩阵.但是由于二次DCT变换使得频谱信息的存储量增加,因此需要考虑算法的计算效率. 低维的频率参数和时间参数能为声音分类提供更多的全局变化信息.图3(3)中的A、D区域主要包含随着时间变化的局部对数谱均值信息,C区域主要体现频谱结构的细化信息,而有利于声音分类的对数谱全局变化情况,主要体现于B区域.为了使用较少的空间获得较多的频谱变化信息,本文选取B区域的15行5列TDMFCC子矩阵作为声音信号的主特征,用于分类识别,其表达式如下: TDMFCC=[c(0,0),…,c(0,4),c(1,0),…, c(1,4),…,c(14,0),…,c(14,4)]T. (19) 图3 TDMFCC矩阵Fig.3 The TDMFCC matrix 实验中用到的鸟叫声来自Freesound[17]声音数据库,具体类别如表1所示.每类声音有50个声音样本,每个样本的采样率为11 025 kHz,量化精度为16 bits,持续时间长度为4~6 s,格式为wav,单声道.随机选择20个样本用于训练,另外30个样本用于测试.为了模拟实际噪声场景,将测试声音样本分别与不同背景噪声分别按40、30、20、10、0 dB的信噪比合成.实验所用的背景噪声分别为高斯白噪声、海浪噪声、溪流噪声,其中高斯白噪声用噪声发生器生成,海浪噪声及溪流噪声从实地采集. 实验直接使用LIBSVM[18]工具箱,选用径向基核函数,采用自动寻优方式设置惩罚因子等参数,利用“一对一”的多分类策略,来对声音信号进行SVM建模分类,得出识别结果. 表1 实验数据Tab.1 Experimental data 实验旨在验证本文所提方法对噪声环境下的鸟叫声分类的有效性,因此分别对MFCC、TDMFCC以及用文中所提的分频段ABAP谱减法降噪后的MFCC(标记为ABAP_MSS+MFCC)、分频段ABAP谱减法降噪后的TDMFCC(标记为ABAP_MSS+TDMFCC)进行SVM建模分类的声音识别实验,前3个为对照实验,第4个为目标实验.针对高斯白噪声、海浪噪声、溪流噪声这3种不同噪声下不同信噪比的平均分类结果如表2所示.而针对这3种不同噪声类型和不同信噪比所对应的实验结果如图4所示. 表2 不同噪声类型下不同信噪比的平均分类结果Tab.2 The average classification rates of different SNRs under different types of noises 由表2的实验结果可以看出,虽然是在高斯白噪声、海浪噪声和溪流噪声这3种不同背景噪声类型下,但是其鸟叫声的平均识别率具有相类似的规律:MFCC的平均识别率最低,而ABAP_MSS+TDMFCC是四个特征中识别率最高的.根据该表的数据可得,TDMFCC比MFCC的分类性能提高了至少4.35%;使用本文提出的ABAP_MSS方法降噪后的MFCC和TDMFCC,比不使用该方法的MFCC和TDMFCC的分类效果更好,其性能分别提高了至少6.07%和11.12%.由此可见,本文提出的经过ABAP_MSS方法降噪后的TDMFCC,识别性能更好,对不同类型的噪声更具有鲁棒性. (b) 海浪噪声下4种特征的分类结果 (c) 溪流噪声下4种特征的分类结果 由图4(a)、(b)、(c)的实验结果柱状图可以看出,无论是平谱噪声还是有色噪声环境下,4种特征的识别率都随着信噪比的减小而降低,但是下降的速度有所不同.MFCC下降的速率最快,TDMFCC次之,而经过降噪后的ABAP_MSS+MFCC和ABAP_MSS+TDMFCC的识别率下降速度分别为次慢和最慢.说明前面两者受噪声干扰较大,而后面两者对噪声具有一定的鲁棒性.当信噪比为40 dB时,4种特征的识别率都较高,在90%以上.而当信噪比下降到20 dB以下时,ABAP_MSS+TDMFCC的识别率与其他3种特征相比,具有显著提高,性能明显优于其他.说明本文提出的ABAP_MSS+TDMFCC具有较好的抗噪功能,尤其是在低信噪比时,比如小于20 dB,效果显著. 针对噪声环境下的鸟叫声分类问题,提出一种经过分频带自适应Bartlett平均周期图谱减法(ABAP_MSS)降噪后提取TDMFCC特征结合SVM分类器对带噪鸟叫声进行分类的方法.不同噪声类型下和不同信噪比下的实验结果证明,该方法的分类性能较现有的MFCC与降噪后的MFCC更优.ABAP_MSS降噪方法能够有效减少音乐噪声和声音失真,削弱噪声干扰.因此,当信噪比较高时,ABAP_MSS+TDMFCC的分类效果略微优于其他方法;但是当信噪比较低时,该方法的分类效果具有显著提高.由此说明,本文提出的ABAP_MSS+TDMFCC具有良好抗噪能力,且适用于带噪鸟叫声的分类.但是,当信噪比处于0 dB以下时,降噪方法可能带来音乐噪声和失真问题,导致分类效果变差.更低信噪比下的分类问题,以及将分类方法推广至其他应用中的研究工作天在进行中.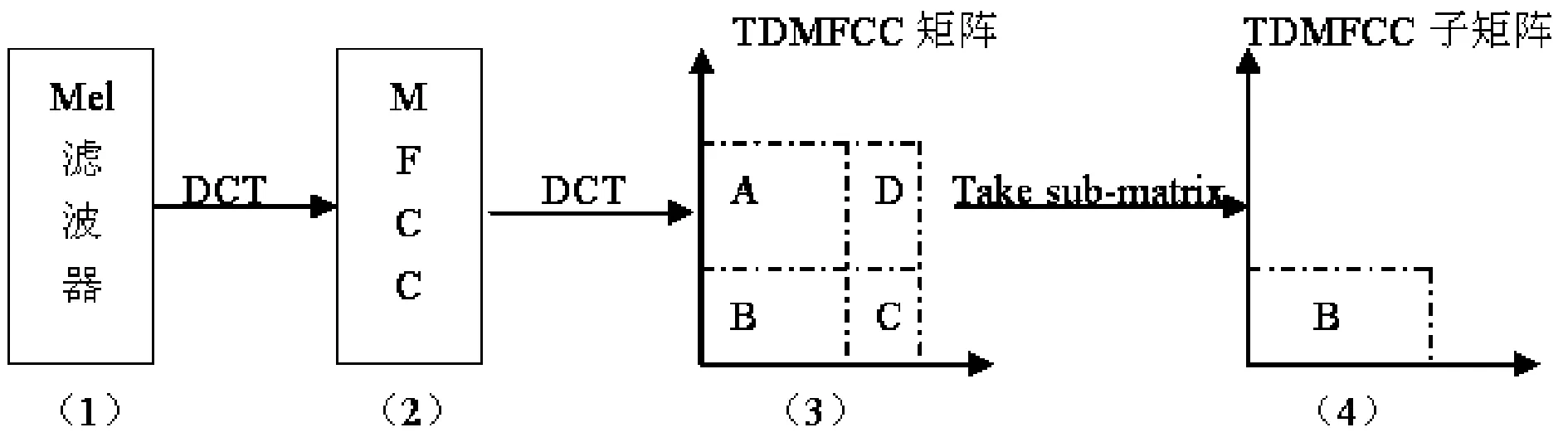
3 结果与分析


4 结论
