BeO分子X1Σ+, a3Π和b3Σ+电子态的光谱性质
2015-08-08胡雪惠张东玲仓玉平
刘 慧,胡雪惠,张东玲,仓玉平
(信阳师范学院 物理电子工程学院,河南 信阳 464000)
0 引言
人们长期致力于BeO、MgO和CaO等碱金属氧化物体系的研究. 获得碱金属氧化物分子准确的光谱信息可以为He-BeO, Ne-BeO, CO-BeO等络合物的研究提供重要数据. 围绕BeO分子的光谱性质, 人们已经开展了许多研究工作. 实验方面, 由于在光谱中观测BeO分子三重态存在诸多困难, 因此, 确定BeO分子基态及激发态的对称性及其光谱性质一直是困扰谱学工作者的难题[1-3];理论方面, 自1963年至今, 许多学者运用多种理论方法对BeO分子的光谱性质进行了研究, 其中有自洽场方法 (SCF)[3-8], 耦合簇方法 (CC)[9-13], 组态相互作用方法 (CI)[14-23]及密度泛函方法 (B3LYP)[24-25]等.
分析已有的文献发现, 尽管有很多研究涉及BeO分子的光谱性质, 但这些工作主要集中于BeO分子基态的光谱信息, 对分子低激发态a3Π和b3Σ+的光谱性质的报道很少, 且只涉及少数几个光谱常数. 同时, 文献中很少涉及各种修正及基组截断等对BeO分子的势能曲线的影响, 导致所获得的光谱常数不够准确. 鉴于此, 为了更准确、更全面地理解BeO分子的光谱特性, 我们对其开展了计算.
1 理论方法
MOLPRO软件包[26]只能使用Abelian点群. BeO分子具有简并对称性, 用C2υ子群代替C∞υ群计算该分子能量. 其对应的不可约表示为a1,b1,b2和a2. 计算中, 将Be原子的2s及O原子的2s2p壳层共8个最外层电子放入活性轨道空间, 包括4个a1, 2个b1及2个b2. 其余的电子则放入2个a1闭壳层轨道. 也即使用6a1/2b1/ 2b2这10个轨道计算X1Σ+, a3Π和b3Σ+电子态的势能曲线.
选择能够获得精确分子相关能的内收缩多参考组态相互作用[27-28]方法(MRCI)对BeO分子开展研究. 计算势能曲线使用的基组是相关一致基, aug-cc-pV5Z (AV5Z). 并对Davidson修正(+Q)[29-30]的影响进行了讨论. 计算中, 核间距在0.05~1.00 nm范围内取值. 为准确描述分子相互作用势, 在平衡位置附近, 采用0.02 nm的小步长进行扫描.
将相关能外推扩展到总能量外推[31-32]来减小基组截断误差, 利用公式(1), 将AV5Z和aug-cc-pVQZ(表示为AVQZ)基组计算的势能曲线外推, 得到外推的势能曲线(表示为Q5).
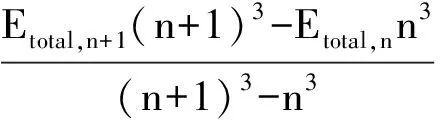
(1)
其中:Etotal, ∞是外推的总能量,Etotal, n和Etotal, n+1分别是由aug-cc-pVnZ和aug-cc-pV(n+1)Z基组计算的总能量.
相对论能量修正是在三阶Douglas-Kroll近似下[33-34]使用cc-pV5Z相对论收缩基计算得到的(记为+DK).核价相关计算使用的基组是aug-cc-pCVQZ. 根据冻结核近似及全电子计算的能量差(记为+CV)获得核价相关能量修正. 拟合同时考虑相对论修正和核价相关修正的外推势能曲线(记为Q5+CV+DK), 得到BeO分子3个态的光谱常数.
求解核运动的振-转Schrödinger方程, 找到了J= 0时BeO分子3个态的全部振动态及与每一振动态对应的振动能级G(υ)和惯性转动常数Bυ等分子常数.
2 结果与讨论
2.1 基组与各种修正对BeO分子光谱常数的影响
为了比较基组和各种修正对BeO分子势能曲线及光谱常数的影响, 利用MRCI理论方法结合AV5Z和AVQZ基组, 计算了核价相关修正、相对论修正及同时包含两种修正BeO分子各电子态的Te,Re及ωe. 限于篇幅, 在表1中仅列出X1Σ+和a3Π电子态的计算结果和实验结果[2].
由表1可见, 无论是MRCI还是MRCI+Q理论方法下, 随着基组增大, a3Π和X1Σ+态的Re均逐渐缩短,ωe均逐渐增大,Te逐渐升高. 容易看出, 随着基组增大到完全基组极限,Te、Re及ωe值逐渐向实验结果靠拢.
通过计算可知, 核价相关修正和相对论修正对a3Π和X1Σ+电子态的势能曲线有较大影响. 以MRCI+Q/ AV5Z理论水平计算为例, 核价相关修正使a3Π和X1Σ+态平衡位置处的能量分别降低了21 742.25 cm-1和21 476.47 cm-1, 相对论修正也使它们的能量分别降低了12 011.19 cm-1和11 989.24 cm-1. 可见, 核价相关修正和相对论修正对两个电子态的势能曲线有重要影响.
核价相关修正和相对论修正对a3Π和X1Σ+电子态的光谱常数有不同的影响. 其中, 核价相关修正对光谱常数的影响较为显著. 与AV5Z结果相比, 核价相关修正使a3Π和X1Σ+的Re变短,ωe变大, 使a3Π态的激发能减小; 相对论修正对光谱常数影响很小, 可以忽略不计.
通过与实验结果[2]比较发现, 当将总能量外推至完全基组极限并进行相对论修正和核价相关修正时, X1Σ+和a3Π电子态的Te,Re及ωe整体与实验结果符合最好. 显然, 即使对于小分子, 要准确描述分子的特性,必须考虑Davidson修正、核价相关修正和相对论修正对分子能量的影响. 因此, 本文利用MRCI+Q/Q5+DK+ CV理论水平的势能曲线进行后续的光谱常数和分子常数的计算.
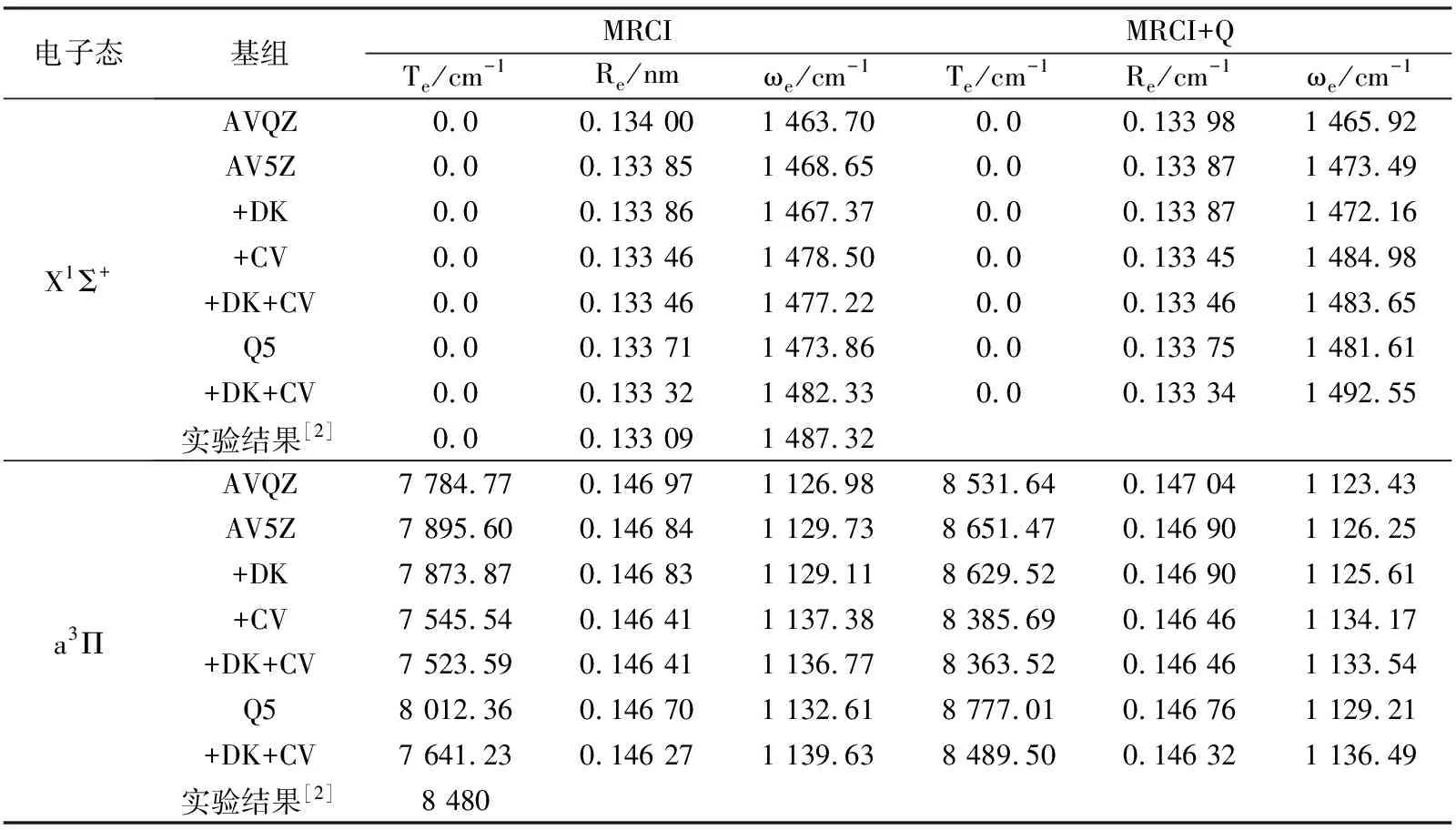
表1 各种修正对BeO分子光谱常数Te, Re及ωe的影响Tab.1 Effects on spectroscopic parameter by the basis sets extrapolation, relativistic and core-valence correlation corrections for BeO molecule
2.2 MRCI+Q/Q5+DK+CV理论水平下BeO分子X1Σ+, a3Π和b3Σ+态的光谱常数
利用MRCI+Q/Q5+DK+CV理论水平下BeO分子X1Σ+, a3Π和b3Σ+态的势能曲线, 拟合得到了它们的光谱常数. 将这些结果列入表2. 同时, 表2中还列出了实验结果[1-3]及与本文研究方法类似、理论水平相当的理论结果[3,14-20]以便于比较. 限于篇幅, 一些利用单参考理论方法计算的结果[1, 4-13,21-25]未列入表2, 例如: 耦合簇方法、自洽场方法、密度泛函方法等. 原因在于, 一方面, 单参考理论方法不能准确反映分子的多组态特性; 另一方面, 利用这些理论方法得到的光谱数据与实验结果相差较大, 不能准确描述分子的性质.
对于X1Σ+, 文献[14-17]采用与本文相同的MRCI理论方法对BeO分子进行计算, 但是, 他们计算中使用的基组普遍偏小, 且均未考虑相对论效应和核价相关效应对该分子能量的影响. 从表2可以看出, 与实验结果[1-2]相比, 他们预测的光谱常数普遍存在Re偏大, 而ωe和ωexe偏小的问题. 文献[18,20]报道了使用MRCI理论方法和较大的基组对BeO分子进行的计算. 他们所得的结果较文献[14-17]的计算精度有所提高. 然而, 同样由于未考虑相对论效应和核价相关效应的影响, 他们预测的Re偏大,ωe和ωexe偏小. 本文在MRCI+Q/Q5+ DK+CV理论水平获得的Re,ωe,ωexe,Be,αe和De与实验结果[1]的相对误差分别只有: 0.18%、0.37%、0.26%、0.42%、0.95%和0.25%,是迄今为止最准确的预测结果.
对于a3Π态, 可以看出, 由于计算中使用了较小的基组且未考虑相对论效应和核价相关效应对分子能量的影响, 文献[14,17]预测的激发能偏低. 它们与较近的实验结果分别相差703 cm-1(8.20%) 和2 183.2 cm-1(25.46%). 显然, 他们计算的势能曲线精度不高. 文献[15]报道的MRD-CI/cc-pVTZ理论方法计算得到的Te与实验结果符合较好, 但其Re和ωe与实验结果偏离较大. 文献[3,19]与实验结果出入较大. 比较而言, 本文对a3Π态的预测结果最准确, 简单计算可知, 除ωexe外, 本文的Te,Re,ωe,Be,αe和De与实验结果[1]的相对误差分别只有: 0.99%、0.01%、0.40%、0.11%、0.06%和0.25%. 这一计算结果是相当准确的.
对于b3Σ+, 由于未找到与之相关的光谱实验报道, 无法将本文预测结果与它们进行比较, 但从X1Σ+、a3Π的计算结果与实验结果的符合情况来看, 本文选择的理论方法可以精确预测BeO分子的势能曲线, 用同样方法计算得到的b3Σ+的势能曲线也理应是合理的, 本文对b3Σ+态光谱常数的预测应该是准确的、可信的.
从上述比较可以看出, 在MRCI+Q/Q5+DK+CV理论水平下, BeO分子X1Σ+, a3Π和b3Σ+态的光谱常数与实验结果[1-3]一致. 这些充分说明在该理论水平下获得到的势能曲线是准确的, 因此这些势能曲线可进一步用于振动迭代计算.
2.3 振动能级及惯性转动常数
基于MRCI+Q/Q5+DK+CV理论水平下确定的BeO分子X1Σ+, a3Π和b3Σ+电子态的势能曲线, 根据Numerov[35]方法求解振-转Schrödinger方程, 得到了3个态J= 0时的全部振动态, 进而计算了每一振动态对应的G(υ)和Bυ等分子常数. 表3和表4分别列出了前11个振动态的G(υ)和Bυ. 同时, 表中还列出了实验结果[3]及其他的理论结果[17-18].

表2 BeO分子X1Σ+, a3Π和b3Σ+电子态的光谱常数Tab.2 Spectroscopic parameters of the X1Σ+, a3Π and b3Σ+ electronic states of BeO molecule
由表3可以看出, 本文计算的X1Σ+态的G(υ)与实验结果[3]完全一致, 最大相对误差只有0.17% (对应于υ= 0). 文献[17]报道的G(υ)与实验结果[3]相差较大, 最大误差达到14.59%(对应于υ= 0). 文献[18]报道的G(υ)与本文结果接近, 和实验结果[3]符合较好. 它们之间的最大误差为0.49%(对应于υ= 0).
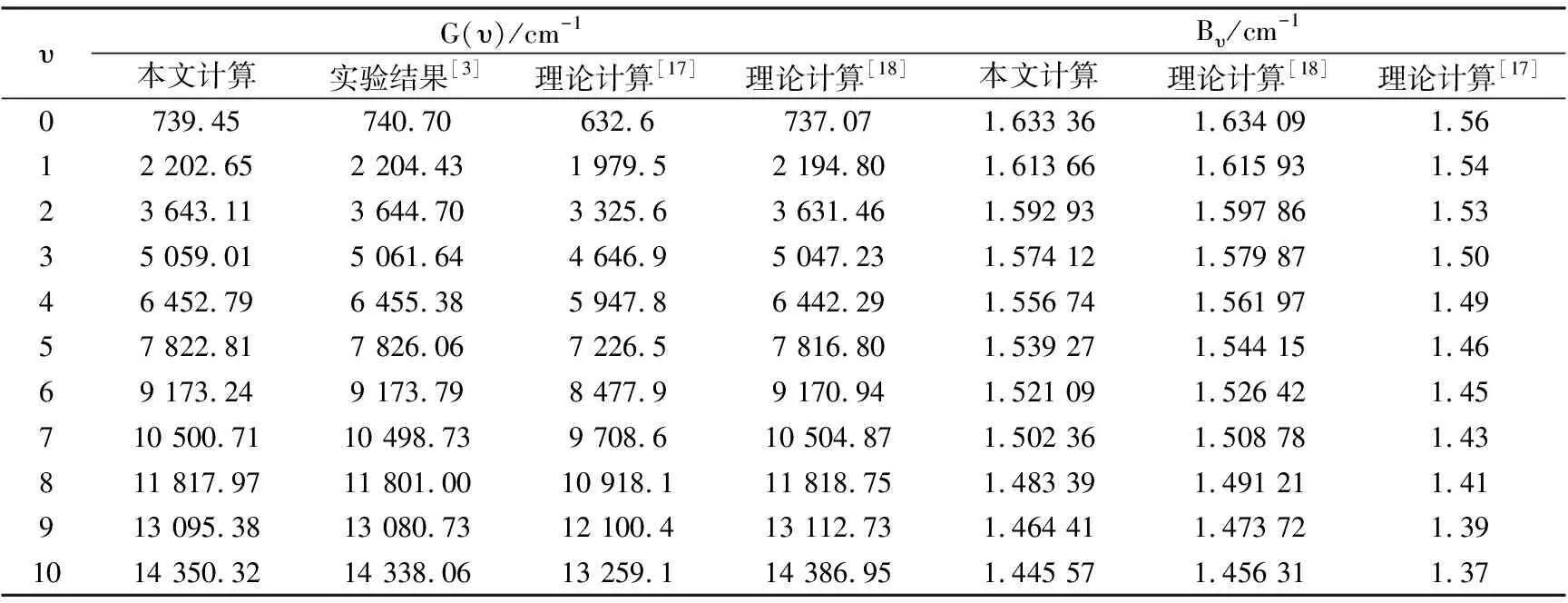
表3 X1Σ+电子态的G(υ)和Bυ与实验结果及其他理论结果的比较Tab.3 The vibrational level and inertial rotation constants for the X1Σ+ electronic state of the BeO molecule
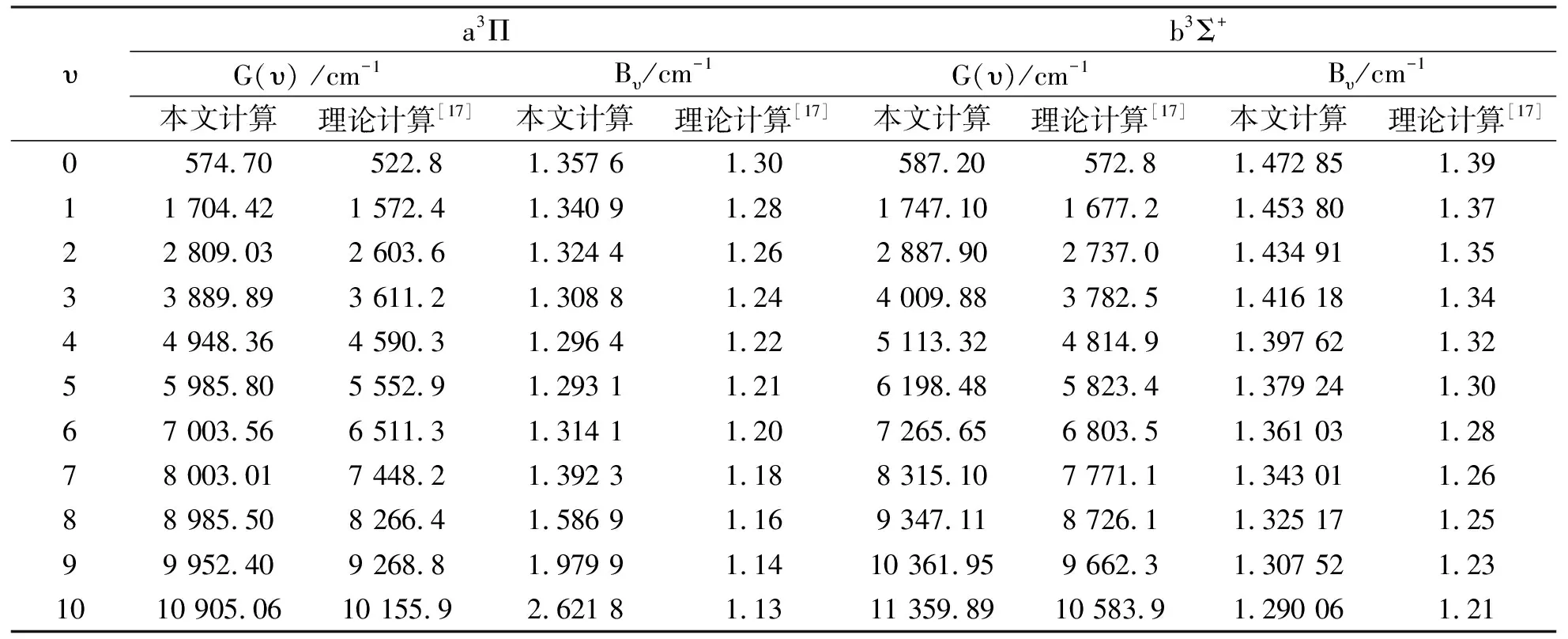
表4 BeO分子a3Π和b3Σ+态的G(υ)和BυTab.4 The vibrational level and inertial rotation constants for the a3Π and b3Σ+ electronic states of the BeO molecule
由于没有关于a3Π和b3Σ+态的G(υ)和Bυ的实验报道, 因此无法将二者比较. 本文在MRCI+Q/ Q5+DK+CV理论水平获得的X1Σ+, a3Π态的光谱常数整体上与实验结果[1-3]符合很好, 预测的基态的振动能级与实验结果一致. 由此可以断定: 采用同样的理论方法预测的a3Π和b3Σ+态的分子常数也应该是准确的. 表4中的数据可以为未来的实验研究提供可靠的参考.
2.4 误差分析
本文计算具有很高的精度, 主要在于以下几个方面: 1) 使用了高水平的内收缩多参考组态相互作用方法和较大的相关一致基来获得分子较准确的势能曲线; 2) 利用两个最大的连续基组AV5Z和AVQZ进行两点总能量外推进行基组截断误差校正; 3) 对势能曲线进行了相对论效应和核价相关效应修正; 4) 利用Davidson计算对MRCI理论方法存在的大小一致性问题进行修正.
3 结论
本文采用Davidson修正的MRCI方法及相关一致基, 于0.05~1.00 nm的核间距范围内计算了BeO分子的X1Σ+, a3Π和b3Σ+态的势能曲线. 利用总能量外推公式, 得到外推的势能曲线. 首次计算了相对论效应及核价相关效应修正, 并获得两种效应修正的外推势能曲线. 拟合势能曲线得到这3个态的光谱常数Te,Re,ωe,ωexe,Be,αe和De. 这些结果与实验结果符合很好. 通过求解核运动的振-转Schrödinger方程, 找到了J= 0时BeO分子X1Σ+, a3Π和b3Σ+的全部振动态及与每一振动态对应的振动能级和惯性转动常数等分子常数. 它们均与实验结果一致. 本文采用的研究方法可以为同类理论研究提供有益借鉴, 所获得的光谱数据可为实验研究提供可靠的参考.
