离散p-Laplace系统周期解的存在性
2015-08-08薛艳昉廖家锋
薛艳昉,廖家锋
(1.信阳师范学院 数学与信息科学学院, 河南 信阳 464000;2.遵义师范学院 数学与计算科学学院, 贵州 遵义 563002)
0 引言
随着计算机科学的应用和发展,差分方程和离散系统的理论研究也越来越受到重视,特别是对差分方程周期解的研究成果较为丰富(参见文献[1-9]等).研究的方法主要是不动点定理、临界点理论等,其中文献[1]在次二次条件下,讨论了离散Hamilton系统周期解的存在性;文献[10]运用鞍点定理讨论了p-Laplace系统解的存在性;文献[11]在非线性项有一部分是次线性的条件下,得到了二阶Hamilton系统周期解的存在.受文献[1,10-11]的启发,本文考虑离散p-Laplace系统周期解的存在性,所得结果推广了文献[1]中的相关结论.
1 预备知识
考虑下面的离散p-Laplace系统(差分方程组):
Δ(φp(Δu(t-1)))+▽F(t,u(t))=0,∀t∈Z,
(1)
其中:Δu(t)=u(t+1)-u(t);φp(s)=|s|p-2s,p>1;F:R×RN→R,Z是正整数集,F(t,x)关于x是连续可微的,关于t是T周期的(T>0);▽F(t,x)表示F(t,x)关于x的梯度.
定义HT={u:Z→RN,u(t+T)=u(t),t∈Z},则HT为Banach空间,其上的范数为
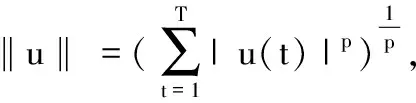
及
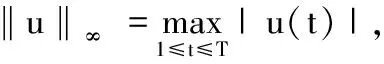
此处|·|表示RN中通常的范数.对u∈HT,令
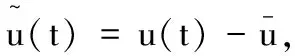
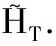
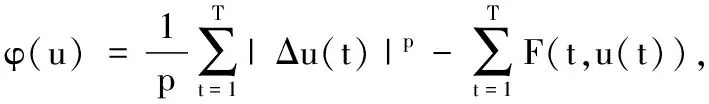
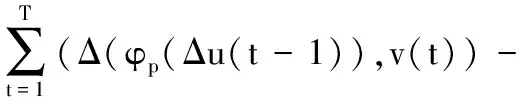

众所周知,系统(1)的周期解等价于泛函φ(u)的临界点,下面的定理就是通过临界点理论,寻找φ(u)的临界点,从而得到系统(1)的周期解.
2 主要结果及证明
定理1 假设F(t,x)满足
(F1)F(t+T,x)=F(t,x);
(F2) 对所有t∈Z[1,T],当|x|→∞时,有
(F3) 对所有t∈Z[1,T],当|x|→∞时,有
(▽F(t,x),x)-pF(t,x)→-∞,
则系统(1)至少有一个T周期解.
证明首先说明φ满足(C)条件,即对任意序列{uk}⊂HT,若φ(uk)有界,并且当k→∞时,
(1+‖uk‖)·‖φ′(uk)‖→0,
则{uk}有一个收敛的子列.
假设{uk}⊂HT,φ(uk)有界,并且当k→∞时,
(1+‖uk‖)·‖φ′(uk)‖→0,
则存在M0>0使得
|φ(uk)|≤M0,(1+‖uk‖)·‖φ′(uk)‖≤M0,
从而有
-(p+1)M0≤pφ(uk)-‖uk‖·‖φ′(uk)‖≤
pφ(uk)-〈φ′(uk),uk〉=
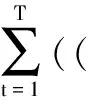
则{uk}有界.事实上,如果{uk}无界,则存在M1>0及{uk}的子序列(仍然用{uk}表示),使得当t∈E0时,
|uk(t)|→∞(k→∞),
其中E0是Z[1,T]的非空子集,Z[1,T]=Z∩[1,T],Z是整数集.
当t∈Z[1,T]-E0时,|uk(t)|≤M1;当t∈E0时,由(F3)知,当k→∞时,有
(▽F(t,uk(t)),uk(t))-pF(t,uk(t))→-∞.
因为F连续可微,所以当t∈Z[1,T]-E0时,存在M2>0,使得
(▽F(t,uk(t)),uk(t))-pF(t,uk(t))≤M2.
综上可知,当k→∞时,对任意t∈Z[1,T],有
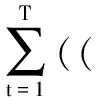
此极限式与已得到的不等式
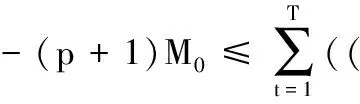
pF(t,uk(t))),
矛盾.故{uk}有界,作为有限维空间HT中的一个有界的序列,{uk}有收敛的子列,从而函数φ满足(C)条件.由文献[12]中的鞍点定理,我们只需要验证下面两个条件成立:
(I1) 对任意x∈RN,当|x|→∞时,有
φ(x+e(t))→-∞,
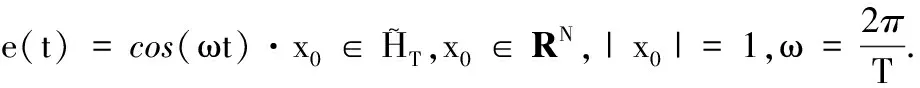
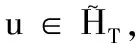
φ(u)→+∞.
由条件(F2)和(F3)可得,对任意t∈Z[1,T],当|x|→∞时,有F(t,x)→+∞.
事实上,由条件(F3)知,对任意M>0,存在M3>0,使得对任意t∈Z[1,T],当|x|>M3时,
(▽F(t,x),x)-pF(t,x)<-M,
也就是对任意|sx|>M3,有
(▽F(t,sx),sx)-pF(t,sx)<-M,
从而有
令s>1,对上述不等式两端从1到s积分得
在上面的不等式中令s→+∞,再结合条件(F2)可得,对任意|x|>M3,有
(2)
由M的任意性即得,当|x|→∞时,有
F(t,x)→+∞.
由式(2)得,当x∈RN,且|x|>M3+1时,有
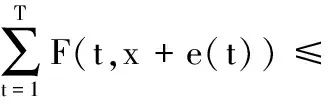
由M的任意性即得,对任意x∈RN,当|x|→∞时,有
φ(x+e(t))→-∞.
最后,证φ满足条件(I2).
由条件(F2)得,对任意δ>0,存在M4>0,使得对任意t∈Z[1,T],当|x|>M4时,有
F(t,x)≤δ|x|p.
因为对任意t∈Z,F(t,x)关于x是连续可微的,所以存在M5>0,使得当|x|>M4时,有
|F(t,x)|≤M5,
从而对任意x∈RN及t∈Z[1,T],有
F(t,x)≤δ|x|p+M5.
(3)
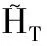
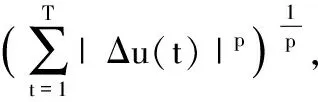
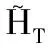
(4)
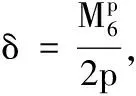
综上,由鞍点定理,φ存在临界点u∈HT,使得
证毕.
定理2 假设F(t,x)满足(F1)以及
(F4) 存在常数C>0,0<μ (▽F(t,x),x)≤μF(t,x); (F5) 存在常数β及t0∈Z[1,T],使得对任意(t,x)∈Z[1,T]×RN,有F(t,x)≥β,并且当|x|→∞时,有F(t0,x)→+∞,则系统(1)至少有一个T周期解. 证明第一步,说明φ满足(C)条件. 假设{uk}⊂HT,φ(uk)有界,并且当k→∞时, (1+‖uk‖)·‖φ′(uk)‖→0, 则存在C1>0使得 |φ(uk)|≤C1,(1+‖uk‖)·‖φ′(uk)‖≤C1. (5) 由条件(F1),(F4)可得,存在常数C2,使得 从而 (p+1)C1≥(1+‖uk‖)·‖φ′(uk)‖-pφ(uk)≥ 〈φ′(uk),uk〉-pφ(uk)= 因为0<μ (6) 由不等式(5)和(6)得 从而存在常数C4,使得对任意k∈N,有 |uk(t)|→+∞. 由条件(F5)得 F(t0,uk(t0))+Tβ→+∞(k→∞). 综上可知,{uk}有界,从而有收敛的子序列,即φ满足(C)条件. 第二步,证φ满足(I1).对任意x∈RN,有 由条件(F5)知,当|x|→∞时,有φ(x+e(t))→-∞. 第三步,证φ满足(I2). 由条件(F4)得,存在C6>0,C7>0,使得 |F(t,x)|≤C6|x|μ+C7. 综上,由鞍点定理,φ存在临界点u∈HT,使得 证毕. 本文的定理1和定理2分别推广了文献[1]中的定理2和定理3.事实上,令p=2即得文献[1]中的相关定理,并且我们的条件(F5)比文献[1]里面定理3中的条件(F7)要弱.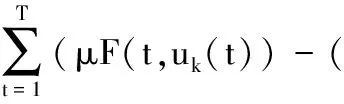
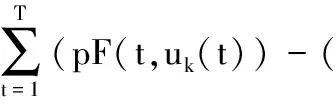
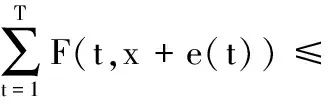
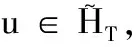
3 讨论
