一类非线性微分系统的严格实用稳定性
2015-08-08叶凯莉
叶凯莉,宋 强, 陈 晨
(1.信阳师范学院 a.工商管理学院; b.数学与信息科学学院, 河南 信阳 464000;2.信阳职业技术学院 数学与计算机科学系, 河南 信阳 464000)
0 引言
在研究微分系统的数量关系时,Lyapunov第二方法是一个基本的技巧.然而如果一个给定的系统是渐近稳定的,这一方法却不能给出解的衰变率任何信息.因此,我们期待当系统的解接近于零解时,其变化下界的估计.为了丰富Lyapunov稳定性的理论,文献[1]定义了严格稳定性的概念和讨论连续系统的严格稳定性准则.Lakshmikantham和Mohapatra[1]运用严格稳定性证明了一致渐近稳定性的结论.Zhang和Fu[2]运用变化的Lyapunov函数研究微分系统严格稳定性.通过运用Lyapunov函数和Razumikhin技巧,文献[3]得到了脉冲微分方程的严格稳定性准则.
以前对微分方程初值问题的研究仅限定在空间变量的扰动,而初始时刻是不变的.在实际情况中,仅有空间变量的变化而没有初始时刻的变化是不可能的.因此,在研究微分系统解的稳定性时考虑变化的初始时刻就很有必要.然而把Lyapunov第二方法运用到微分系统变化的初始时刻时却是困难的.这种困难是因为初始时刻不同的稳定性与稳定的经典概念有很大不同.稳定的经典概念是关于零解的稳定性,但初始时刻不同的稳定性则是关于初始位置和初始时刻都不同的两个解的稳定性[4].比较和衡量两个解的不同时有两个方向.一个方向是该方法的参数变化.例如,在文献[4]中,参数变化的方法被引入来讨论这种情况.近来参数的变化模式化被用来研究初始时刻不同的未扰动和扰动的系统. 作者们构造了未扰动的微分系统和扰动系统,通过运用变化初始时刻的比较系统结果,得到了初始时刻不同的稳定性和指数渐近稳定性.另一方向是运用微分不等式技巧.关于初始时刻微分不等式的问题首先在文献[4]中提出.运用这一方法,人们可以比较从不同的初始点开始的微分系统的解.文献[5]通过运用微分不等式技巧,得到初始时刻不同的微分方程稳定性的结论.就我们所知,初始时刻不同的微分方程的严格稳定性目前还没人研究.为了丰富和推广Lyapunov稳定性的理论[6-7],我们定义了初始时刻不同的严格稳定性的概念并讨论了几个严格稳定性的准则.在本文中,我们定义了非线性微分方程初始时刻不同的严格稳定性的概念.应用两个Lyapunov函数的方法,分别给出了非线性微分系统初始时刻不同的各种严格稳定性的充分条件.最后我们提出了一个非线性微分方程初始时刻不同的解的比较定理,并运用该比较定理证明了非线性微分系统初始时刻不同的严格稳定性准则.
1 定义及引理
在一个实n维欧几里得赋范空间考虑微分系统
x′=f(t,x),
(1)
其中f∈C[R+×Rn,Rn].令x*(t)=x*(t,t0,y0)和x(t)=x(t,τ0,x0))分别为系统(1)的过初始值(t0,y0)和(τ0,x0)的解.假设x*(t)是将要研究稳定性准则给定的解.令η=τ0-t0且记S(x*,ρ)={x∈Rn:‖x-x*(t)‖<ρ},S(ρ)={x∈Rn:‖x‖<ρ}.我们定义下面的函数类空间:
K={a∈C(R+,R+):a是严格增的且a(0)=0}.
当V∈C[R+×Rn,Rn],定义动力系统(1)的广义导数为:
hf(t,x))-V(t,x)),
hf(t,x))-V(t,x)).
对于初时时刻不同的非线性动力系统,引入下面的稳定性的定义.
定义1 系统(1)的解x*(t)=x*(t,t0,y0)是:
(S1) 严格等价稳定的,如果对于任意给定的ε1>0和某个t0∈R+,存在一个δ1=δ1(t0,ε1)>0和σ1=σ1(t0,ε1)>0可由‖x0-y0‖<δ1,|η|<σ1得出‖x(t+η,τ0,x0)-x*(t,t0,y0)‖<ε1对所有的t≥t0成立,且对每一个0<δ2<δ1,都存在一个0<ε2<δ2和σ2=σ2(t0,ε2)>0,可由δ2<‖x0-y0‖,|η|<σ2得出ε2<‖x(t+η,τ0,x0)-x*(t,t0,y0)‖对所有的t≥t0成立;
(S2) 严格一致稳定的,如果(S1)成立且δ和σ的取值与t0∈R+无关;
(S3) 严格吸引的,如果对于给定的α1>0,ε1>0和某个t0∈R+,对每一个0<α2≤α1,都存在一个ε2<ε1,σ=σ(t0,ε1,ε2)>0和T1=T1(t0,ε1),T2=T2(t0,ε2)可由α2<‖x0-y0‖≤α1,|η|<σ得出ε2<‖x(t+η,τ0,x0)-x*(t,t0,y0)‖<ε1,对每一个t0+T1≤t≤t0+T2都成立;
(S4) 严格一致吸引的,如果(S3)成立且σ,T1和T2与t0∈R+无关;
(S5) 严格等价渐近稳定的,如果(S3)成立且解x*(t)=x*(t,t0,y0)是稳定的;
(S6) 严格一致渐近稳定的,如果(S4)成立且解x*(t)=x*(t,t0,y0)是一致稳定的.
引理1[1]假设
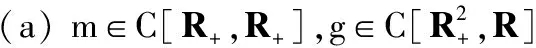
g1(t,m(t)),t∈R+,其中
(b)r1(t)=r1(t,t0,u0)是u′=g(t,u),u(t0)=u0≥0,t0≥0在[t0,∞)的最大解,
则m(t0)≤u0蕴涵着m(t)≤r1(t),t≥t0.
引理2 假设
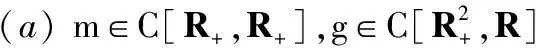
g2(t,m(t)),t∈R+,其中
(b)r2(t)=r2(t,t0,v0)是v′=g(t,v),v(t0)=v0≥0,t0≥0在[t0,∞)的最大解.
则m(t0)≥v0蕴含着m(t)≥r2(t),t≥t0.
2 主要结果
下面将给出初始时刻不同的非线性微分方程严格稳定性的几个结论.
定理1 假设:
(i) 对每一个V1∈C[R+×S(x*,ρ),R+],V1(t,x)关于x是局部Lipschitzian的,V1(t,0)≡0且对(t,x)∈R+×S(ρ),有
b1(‖x‖)≤V1(t,x)≤a1(t,‖x‖),a1∈CK,b1∈K
和
D+V1(t,x)≤0;
(2)
(ii)) 对每一个V2∈C[R+×S(x*,ρ),R+],V2(t,x)关于x是局部Lipschitzian的,V2(t,0)≡0且对(t,x)∈R+×S(ρ),
b2(‖x‖)≤V2(t,x)≤a2(‖x‖),a2,b2∈K
和
D-V2(t,x)≥0.
(3)
那么系统(1)的解x*(t)=x*(t,t0,y0)是严格等价稳定的.
证明对于任意给定的0<ε1<ρ和t0∈R+.选择δ1=δ1(t0,ε1)>0和σ1=σ1(t0,ε1)>0使得
a1(t0,δ1) (4) 假设‖x0-y0‖<δ1和|η|<σ1蕴涵着 ‖x(t+η,τ0,x0)-x*(t,t0,y0)‖<ε1,t≥t0. (5) 如果假设不成立,那么一定存在系统(1)一个解x(t)=x(t,τ0,x0)当‖x0-y0‖<δ1,|η|<σ1和t2>t1>τ0时满足 (6) 由式(2)和引理1,不难证明V1(t,x)关于t是单调递减的,且V1(t,x(t+η,τ0,x0)-x*(t,t0,y0))≤V1(t0,‖x0-y0‖),t≥t0.由式(6)我们得到 b1(ε1)=b1(‖x(t2+η,τ0,x0)-x*(t2,t0,y0)‖)≤ V1(t2,x(t2+η,τ0,x0)-x*(t2,t0,y0))≤ V1(t0,‖x0-y0‖)≤a1(t0,‖x0-y0‖)< a1(t0,δ1),t≥t0, 这与式(4)矛盾,于是假设成立. 另一方面,令0<δ2<δ1,选择ε2=ε2(t0,δ2)<δ2和σ2=σ2(t0,ε2)>0使得 a2(ε2) (7) 假设δ2<‖x0-y0‖和|η|<σ2蕴含着 ε2<‖x(t+η,τ0,x0)-x*(t,t0,y0)‖,t≥t0. (8) 如果假设不成立,那么一定存在系统(1)一个解x(t)=x(t,τ0,x0)当δ2<‖x0-y0‖和|η|<σ2且t4>t3>τ0时满足 (9) 由式(3)和引理2,不难证明V2(t,x)关于t是单调递减的,且V2(t,x(t+η,τ0,x0)-x*(t,t0,y0))≥V2(t0,‖x0-y0)‖,t≥t0.结合式(9),我们得到 a2(ε2)=a2(‖x(t3+η,τ0,x0)-x*(t3,t0,y0)‖)≥ V2(t3,x(t3+η,τ0,x0)-x*(t3,t0,y0))≥ V2(t0,‖x0-y0‖)≥b2(‖x0-y0‖)> b2(δ2),t≥t0, 这与式(7)矛盾,于是假设成立. 由式(5)和(8),可以得出系统(1)的解x*(t)=x*(t,t0,y0)是严格等价稳定的.证毕. 推论1假设定理1中a1∈CK,a1(t,λ)被a1∈K,a1(λ)代替,而其余条件成立,那么系统(1)的解x(t)=x(t,t0,x0)是严格一致稳定的. 定理2 假设定理(1)除了条件(2)和(3)分别被 D+V1(t,x)≤-c1(‖x‖),c1∈K (10) 和 D-V2(t,x)≥-c2(‖x‖),c2∈K (11) 代替外,其余条件成立,那么系统(1)的解x(t)=x(t,t0,x0)是严格等价渐近稳定的. 证明首先,我们指出尽管式(10)能推出式(2),但式(11)并不能推出式(3).我们只能得出系统(1)的解x(t)=x(t,t0,x0)是等价稳定的.即对每一个给出ε1,都存在一个δ1=δ1(t0,ε1)>0和σ=σ(t0,ε1)>0可由‖x0-y0‖<δ1,|η|<σ得 ‖x(t+η,τ0,x0)-x*(t,t0,y0)‖<ε1,t≥t0. (12) 为了证明定理2,需要证明系统(1)的解是严格吸引的.对任一给定的ε1>0,限定α1=α1(ε1)≤δ1.由式(12)有‖x0-y0‖<α1,|η|<σ蕴含着 ‖x(t+η,τ0,x0)-x*(t,t0,y0)‖<ε1,t≥t0. 令‖x0-y0‖<α1和|η|<σ,于是假设存在一个t*∈[t0,t0+T],其中T=T(ε1)>a1(t0,α1)/c1(α1),使得 ‖x(t*+η,τ0,x0)-x*(t*,t0,y0)‖<α1. (13) 对系统(1)的解x(t)=x(t,τ0,x0)成立.如果假设不成立,则有 ‖x(t+η,τ0,x0)-x*(t,t0,y0)‖≥α1, (14) t∈[t0,t0+T].由定理1(i)和式(14),我们有 b1(α1)≤b1(‖x(t0+T+η,τ0,x0)- x*(t0+T,t0,y0)‖)≤ V1(t0+T,x(t0+T+η,τ0,x0)- x*(t0+T,t0,y0))≤ V1(t0,‖x0-y0‖)- a1(t0,‖x0-y0‖)-c1(α1)T< a1(t0,α1)-c1(α1)T 这个矛盾表明存在一个t*∈[t0,t0+T],使得 ‖x(t*+η,τ0,x0)-x*(t*,t0,y0)‖<α1. 又由于系统(1)的解x*(t)=x*(t,t0,y0)是等价稳定的,可以推出‖x(t+η,τ0,x0)-x*(t,t0,y0)‖<ε1,t≥t0+T≥t*,这表明存在一个T1>T使得 ‖x(t0+η,τ0,x0)-x*(t0,t0,y0)‖<ε1. (15) t≥t0+T1.现在对任一0<α2<α1,选择ε2<ε1,使得 b2(α2)>a2(ε2),0<ε2<α2. 假设α2<‖x0-y0‖<α1.定义 且T2=T1+t*.由式(15)和定理1(ii),可以得到 a2(‖x(t+η,τ0,x0)-x*(t,t0,y0)‖)≥ V2(t,x(t+η,τ0,x0)-x*(t,t0,y0))≥ V2(t0,‖x0-y0‖)- b2(‖x0-y0‖)- b2(α2)-c2(ε1)(t-(t0+T1)) 对任一t∈[t0+T1,t0+T2]成立.又因为t-(t0+T1)≥t*,所以可得出 a2(‖x(t+η,τ0,x0)-x*(t,t0,y0)‖)≥ 这就证明了 ‖x(t+η,τ0,x0)-x*(t,t0,y0)‖>ε2, (16) t∈[t0+T1,t0+T2].由式(15)和(16)有ε2<‖x(t+η,τ0,x0)-x*(t,t0,y0)‖<ε1,t∈[t0+T1,t0+T2].证毕. 推论2 假设定理2的条件a1∈CK,a1(t,λ)替换为a1∈K,a1(λ),其余条件不变,那么系统(1)的解x(t)=x(t,t0,x0)是严格一致渐近稳定的. 下面,证明一个比较定理.考虑比较系统 (17) 定义2 比较系统(17)是 (S1)严格稳定的.如果对于任给的ε1>0和某个t0∈R+,都存在一个δ1=δ1(t0,ε1)>0可由u0<δ1推出u1<ε1,t≥t0,且对每一个0<δ2<δ1,都存在一个0<ε2<δ2可由δ2 (S2)严格一致稳定的.如果对所有的t0∈R+,(S1)都成立; (S3)严格吸引的.如果对于给定的α1>0,ε1>0和t0∈R+,且对每一个0<α2≤α1,都存在一个ε2<ε1和T1=T1(t0,ε1),T2=T2(t0,ε2)可由u0<α1得出u1<ε1;α2 (S4)严格一致吸引的,如果对所有的t0∈R+,(S3)都成立; (S5)严格一致渐近稳定的,如果(S3)成立且比较系统是稳定的; (S6)严格渐近稳定的,如果(S4)成立且比较系统是一致稳定的. 定理3 假设定理1除了条件(2)和(3)分别被 D+V1(t,x)≤g1(t,V1(t,x)) (18) 和 D-V2(t,x)≥g2(t,V2(t,x)), (19) 那么由比较系统(17)的稳定性可以推出系统(1)相应的各种稳定性. 提出了非线性微分系统的初始时刻不同时严格稳定性的概念,证明了非线性微分系统初始时刻不同的几个严格稳定性的判定准则.这在解决初始时刻不同非线性微分系统的问题时能提供更好的前景.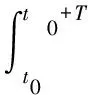
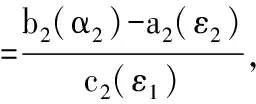
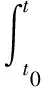
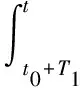
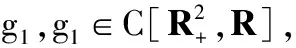
3 结论
