媒体宣传影响下的脉冲控制双菌株SIR传染病模型
2015-08-08郭淑利
郭淑利,张 萍
(信阳师范学院 数学与信息科学学院, 河南 信阳 464000)
0 引言
传染病是由各种病原体引起的能在人与人、人与动物、动物与动物之间相互传播的一类疾病,传染病严重危害人类健康与社会经济发展.传染病动力学是对传染病进行定量研究的一种重要方法,是根据疾病的发生及其在种群内或种群间传播和发展的规律,建立能反映疾病发展变化过程和传播规律的数学模型,通过对模型动力学形态的定性、定量分析,揭示其流行规律,预测其发展趋势,寻求防控疾病的最优策略.不同的传染病,人为干扰、防控的方式不同,如乙肝,常用的免疫策略是在固定时刻T进行脉冲式预防接种,刻画这种免疫策略的SIR传染病模型可用下列方程组表示[1-3]:
(1)
模型(1)刻画了疾病的病原体只有一种菌株的情形,然而,有许多传染病,如肺结核(TB)、细菌性肺炎(Bacterial pneumonia)、丙型肝炎(HCV)、艾滋病(AIDS)、淋病(Gonorrhea)、登革热(Dengue Fever)、流感(Influenza)等,引起这些疾病的病原体的表现形式有许多种,即病原体有多种菌株.近年来,多菌株传染病动力学的数学建模与研究已引起国内外许多专家、学者的兴趣[4-7].
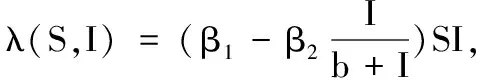
本文沿用文献[10]中的发生率形式,建立并研究受媒体宣传影响和脉冲控制的双菌株SIR传染病模型.
1 模型
假定总人口为常数,在系统(1)的基础上,考虑媒体宣传影响和脉冲控制的双菌株SIR传染病模型可用如下的脉冲微分方程组表示:
(2)
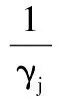
由于系统(2)中最后一个方程是独立的,所以只需考虑如下3维系统即可.
(3)
2 疾病消除周期解的存在性和稳定性
对于系统(3),与没有控制措施的模型一样,首先研究无病平衡解的存在性和稳定性.为此假设Ij≡0(j=1,2).于是有
(4)
系统(4)是一个接种周期为T的周期系统,所以只需研究系统在任何一个脉冲区间(nT,(n+1)T)上解的行为即可.在该区间内,
S(t)=1+(S(nT+)-1)exp(-b(t-nT)),
t∈(nT,(n+1)T).在时刻t=(n+1)T实施一次免疫接种,
S((n+1)T+)=
(1-p)(1+(S(nT+)-1)exp(-bT)).
(5)
记S(nT+)=Sn,则由式(5)可得如下差分方程:
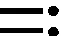
(6)
差分方程(6)存在唯一的正平衡态
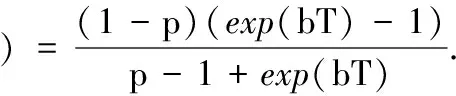
(7)
由于|f′(S*)|=(1-p)exp(-bT)<1,因此S*存在且局部稳定,并且可以证明S*也是全局稳定的.因此,在区间(nT,(n+1)T]内,
S(t)=(1+(S*-1)exp(-b(t-nT)))=
(1+(S*-1)exp(-b(t+T-(n+1)T)))=
S(t+T),t∈(nT,(n+1)T).
(8)
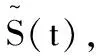
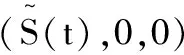
(9)
当t∈(0,T)时,设方程(9)的基解矩阵为
令Φ1(0)=E,计算可得
其中
当t=T时,
故在区间[0,T]上,
其特征乘子分别为
(10)
根据Floquet定理,当|λk|<1(k=1,2,3)时,疾病消除周期解稳定.
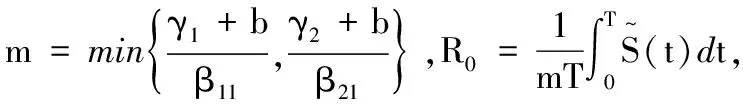
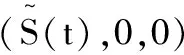
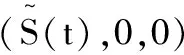
证明当R0<1时,对于充分小的ε>0,下面不等式总成立.
(11)
根据解的正性,由系统(3)可得
(12)
由比较定理可得
(γj+b))dρ)=
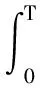
由于当t→∞时,n→∞,结合不等式(11)得到
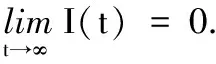
证毕.
3 疾病的持续生存性
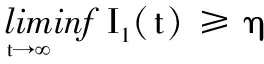
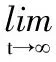
由系统(3)中第一个方程可知,
其比较系统
(13)
收敛于
当Ij≡0时,在区间(nT,(n+1)T]上,
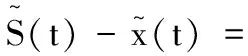
记
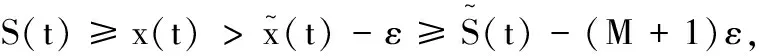
这里,
βj1(M+1)ε).
于是,当t∈(t*+nT,t*+(n+1)T]时,
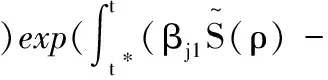
(γj+b)+Lj(ε))dρ)=
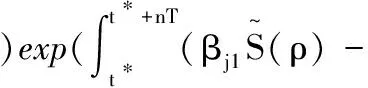
(γj+b)+Lj(ε))dρ)≥
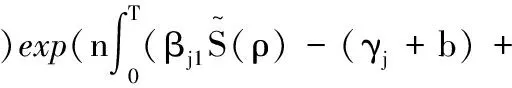
Lj(ε))dρ)exp(-(γj+b)T+Lj(ε)T).
利用R0>1以及ε的任意性得到
因此,
Ij(t)≥Ij(t*)exp((-(γj+b)+
Lj(ε))T)exp(nΨj(ε)),
(14)
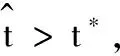
下证疾病一致持续生存.事实上,疾病的弱持续生存保证了至少存在c>0及t1>t*,使得I1(t1)>c或I2(t1)>c至少一个式子成立.
1) 若当t>t1时,总有I1(t1)>c或I2(t1)>c成立,则取η=c>0,定理得证.
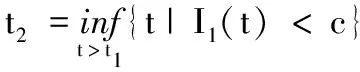
不失一般性,假定t1∈(n1T,(n1+1)T],取n2∈Z+,使e(γ1+b)T 否则,∀t∈((n1+1)T,(n1+1+n2)T],有I1(t) I1((n1+1+n2)T)≥I1((n1+1)T)en2Ψ1. (15) 另一方面,由系统(3)中第二个方程知, 所以,I1((n1+1)T)≥ce-(γ1+b)T,于是由式(15)可知,I1((n1+1+n2)T)≥ce-(γ1+b)Ten2Ψ1>c,矛盾.因此,必存在t3,使I1(t3)≥c.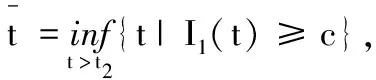

4 结论