一类具有时滞和反馈控制作用的离散竞争系统的渐近行为
2015-08-08向宇
向 宇
(湖北民族学院 理学院, 湖北 恩施 445000)
0 引言
近年来,竞争模型的研究一直受到生物学家和数学家的高度关注.在种群动力学中,两种群Lotka-Volterra竞争模型又是十分著名的模型.过去的数十年里,许多研究者对各类时滞Lotka-Volterra竞争模型的持久生存性、绝灭性以及正解的稳定性进行了研究[1-4].刘显清等在文献[2]中提出了一类具有时滞离散竞争系统
(1)
其中:y1(n)和y2(n)分别表示两竞争种群在第n代的密度;r1(n)和r2(n)分别为两种群在第n代的自然增长率;a1(n)和a2(n)为第n代种群y1和y2对它们自身的种内作用;c1(n)和c2(n)表示第n代种群的种间作用.上述所有参数都为连续有界的正参数,M为正整数.
考虑生态系统在现实世界中往往受到外界力量的持续干扰.把这种扰动函数控制变量看作反馈控制,文献[5-7]及其文献对这方面主题进行了广泛研究.
基于上述讨论,建立如下具有时滞和反馈控制的离散竞争系统:
(2)
n=0,1,2,…;且满足初始条件yi(φ)≥0,ui(φ)≥0,yi(0)>0,ui(0)>0,i=1,2,
φ∈{-L,-L+1,…,0},L=max{M,τ1,τ2}.
(3)
其中u1和u2为控制变量.Δu1(n)=u1(n+1)-u1(n),Δu2(n)=u2(n+1)-u2(n)表示一阶向前差分算子,且0 定义 其中{B(n)}是定义在非负整数集Z+上的有界序列.同时,定义当a>b和a,b∈Z+时, 定义1 如果存在正常数hi,κi,Hi和Ki,对系统(2)的任意正解(y1(n),y2(n),u1(n),u2(n))满足 (4) 那么系统(2)称为持久生存. (5) 引理1[8]假设y(n)在n∈[c,+∞)的条件下满足y(n)>0和 y(n+1)≤y(n)exp(r(n)(1-αy(n))), (6) 其中,α是一个正常数且c∈Z+,那么 (7) y(n+1)≥y(n)exp(r(n)(1-αy(n))), (8) 其中α为常数,使得αH>1,d∈Z+,那么 (9) 命题1 系统(2)的任意正解(y1(n),y2(n),u1(n),u2(n))满足 (10) 其中, (11) (12) (13) i,j=1,2,i≠j;ε>0为充分小的常数. y1(n+1)≤y1(n)exp(r1(n)). (14) 对于n≥M,p=0,1,2,…,M,有 (15) 那么 (16) 它等价于 (17) 因此,根据式(17),可得 y1(n)exp(r1(n)(1- (18) 又由引理1,可知 (19) 类似可推出 (20) (21) 其中 (22) 命题2 假设 (23) min{Δ1H1,Δ2H2}>1, (24) 那么系统(2)的任意正解(y1(n),y2(n),u1(n),u2(n))满足 (25) 其中 (26) Hi,Ki和Δi定义在(11)-(13)上. y1(n+1)≥y1(n)exp(r1(n)-(H1+ε)· (27) 容易得到 (28) 也就是说 r1(i)))=y1(n)G1, (29) 其中 (K1+ε)d1(i)-r1(i))). (30) 结合式(13)、(29)及系统(2)的第一个方程得出 y1(n+1)≥y1(n)exp((r1(n)-c2(n)-(K1+ε)· y1(n)exp((r1(n)-c2(n)-(K1+ε)· (31) 因此,应用引理2及令ε→0,由式(13)、(23)、(24)和(31)可知 (32) 类似地,由系统(2)的第二个方程,我们容易证明 (33) (34) 其中 (35) u2(n)的结论可以类似得出.证毕. 基于上述命题,我们有如下定理1. 定理1 假设条件(23)和(24)成立,那么系统(2)是持久生存的. 定理2 如果不等式(23)和(24)成立.进一步,存在常数η>0,使得 (36) 那么系统(2)的正解是全局稳定的,且Hi定义在式(11)上. 步骤1 令 (37) 则由系统(2)的第一个方程可得 |(lny1(n)+r1(n)- (38) 由中值定理,有 (39) (40) 由式(38)和(40)知 ΔV11(n)=V11(n+1)-V11(n)≤ (41) 步骤2 令 (42) 通过简单计算可得 ΔV12(n)=V12(n+1)-V12(n)= (43) 步骤3 令 (44) 由系统(2)的第三个方程,有 ΔV13(n)=V13(n+1)-V13(n)= |(1-f1(n))u1(n)+g1(n)y1(n-τ1)- (45) 步骤4 令 (46) 容易计算得到 ΔV14(n)=V14(n+1)-V14(n)= (47) 现在定义 V1(n)=V11(n)+V12(n)+V13(n)+V14(n). (48) 那么由式(41)、(43)、(45)和(47)可得 ΔV1(n)=ΔV11(n)+ΔV12(n)+ΔV13(n)+ΔV14(n)≤ (49) 通过类似的讨论,定义 V2(n)=V21(n)+V22(n)+V23(n)+V24(n), (50) 其中 (51) 同样可得, ΔV2(n)=ΔV21(n)+ΔV22(n)+ΔV23(n)+ΔV24(n)≤ (52) V(n)=V1(n)+V2(n). (53) 易得当n∈Z+时,V(n)≥0.根据式(36)和(51),对任意小的ε,存在一个正整数n3,使得当n≥n3时,yi(n)≤Hi+ε,且V(n3+L)<+∞.又由式(36),存在η>0,当ε>0充分小时,有 (54) 因此,对于n≥n3+L,根据式(49)和(52)-(54)可得 ΔV(n)=ΔV1(n)+ΔV2(n)≤ (55) 对式(55)两边从n3+L到n累加,可得 (56) 这意味着对于任意的n≥n3+L,有 (57) 因此, (58) 容易看出,当n→+∞时, 即 (59) 文献[2]研究了一类具有时滞作用的离散竞争系统,并且得到了系统持久生存性和正解的全局稳定性的充分条件.本文在文献[2]的基础上进一步考虑反馈控制作用的影响,得到相应的理论结果.在后续工作中,我们将进一步考虑周期或概周期环境作用下该系统的渐近行为.1 预备知识
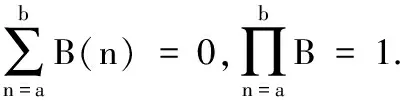
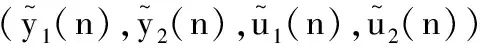
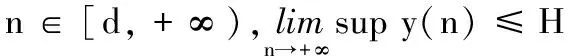
2 持久生存性
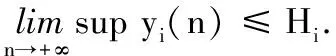
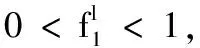
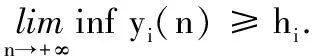
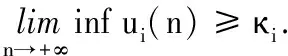
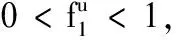
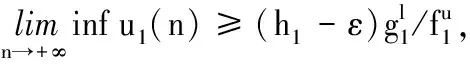
3 正解的全局稳定性
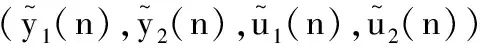
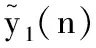
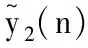
4 结语
