一类带有扩散的捕食模型的非常数正解
2015-08-08周红玲
沈 林,周红玲,赵 中
(黄淮学院 数学科学系, 河南 驻马店 463000)
0 引言
捕食模型是种群动力学研究的核心内容.由于三种群捕食系统具有丰富的动力学行为,因此,对三种群捕食系统研究较多.1969年Ayala[1]通过实验证明了两个捕食者(果蝇)和同一食饵可以共存.为了模拟Ayala的实验,研究者们建立了诸多三种群捕食模型.Armstrong和McGehee[2]讨论了如下模型:
(1)
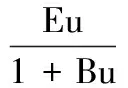
文献[4-5]研究表明,对于居住于海底的一些鱼类,捕食和竞争关系对其死亡率(依赖于密度)有重要影响.文献[6-8]研究了捕食者带有死亡率(依赖于密度)的生物模型.
考虑到空间分布不均匀性,文献[9]研究了一类具有扩散项的三种群捕食系统:
(2)
并讨论了系统的全局吸引性和正常数解的局部稳定性和全局稳定性.
本文在文献[9]的基础上进一步研究在齐次Neumann边界条件下带有扩散系数的如下反应扩散方程:
(3)
其中:Ω∈Rn是有界光滑区域;n是∂Ω上的单位外法向量;d1,d2,d3,a,c,d,m均为正常数;u为食饵种群;v,w为捕食种群;d1,d2,d3分别为三种群的扩散率.模型中参数的生物意义可参见文献[9].
(4)
1 正常数解的稳定性
记U=(u,v,w),G(U)=(G1(U),G2(U),G3(U)).首先给出以下记号:
0 (5) H<1+d. (6) 定理1 若条件(5)和(6)成立,则系统(4)的正常数解是渐近稳定的. ψi(λ)=λ3+A1iλ2+A2iλ+A3i, 其中 A1i=(d1+d2+d3)μi-(a11+a33), (a11(d2+d3)+a33(d1+d2))μi+ a11a33-a12a21-a13a31, ((a11a33-a13a31)d2-a12a21d3)μi+a12a21a33. 容易验证在条件(5)和(6)成立时,a11<0,计算可得:A1i>0,A2i>0,A3i>0,A1iA2i-A3i>0(∀i≥1),所以∀i≥1,ψi(λ)的根λi,1,λi,2,λi,3的实部都小于零. 下面证明存在正常数δ使得Re{λi,1},Re{λi,2},Re{λi,3}≤-δ(∀i≥1).记λ=μiζ,则 (d1d2+d2d3+d3d1)ζ+d1d2d3, 定理2 令Λ是固定的常数,若(u,v,w)是系统(4)的任意正解,则 (7) 证毕. (8) 系统(4)的每一个正解(u,v,w)都满足 (9) 由Harnack不等式[11]可知,存在一个正常数C*=C*(Ω,d1,d2,d3,Λ)使得 (10) (11) 把(ui,vi,wi)代入系统(4)中,然后在Ω上积分可得 (12) (13) 同时结合式(11)可得u*≡0或v*≡0或w*≡0. (i)u*≡0 (ii)w*≡0,u*≢0 (14) 由Lp估计和嵌入定理[12]可知:存在Wi的一个子列(仍记为Wi)满足:Wi→W,(i→∞).W≥0且W≢0,代入式(14)可得: (iii)v*≢0,u*,w*≢0 (u*,w*)满足: (15) 其中:C=C(Λ,ε),ε为Young不等式中非常小的正数. 利用Poincare不等式 上面的不等式可转化为: 由条件(5)可知上式不成立.所以v*≢0.证毕. 通过以上分析可知:当食饵u和捕食者w的扩散系数较大时,若生态系统能够保持平衡,则该平衡解有下界. 利用度理论以d3为参数来讨论系统(4)非常数正解的存在性.设Λ,d1,d2为固定正值,Λ满足条件(5)且H>d+1. (16) 若U是(16)的一个正解当且仅当F(U)=U-(I-Δ)-1{D-1G(U)+U}=0,U∈X+,其中(I-Δ)-1是齐次Neumann条件下(I-Δ)的逆算子.若F(U)≠0,U∈∂B,则可以定义deg(F(·),0,B). 记 (17) (18) 则可得下面的引理. 引理2 假设条件(5)及H>d+1且 d2≥d1,1+2d≥k (19) 进而可得: (20) 下面可证当d3充分大时,系统(4)存在非常数正解. 证明由引理2知,存在一个正常数ρ2,使得d3≥ρ2时(20)成立,且 (21) 下面将用反证法证明,对任意的d3≥ρ,系统(4)至少有一个非常数正解,采用拓扑度的同伦不变性得到矛盾,从而证明此结果. m(t)=tm+(1-t)m0,t∈[0,1],m(0)=m0. 同时对系统(4)把m用m(t)替换掉,则可得到一个新的方程组,把它记为系统(4t).其对应的G(U)用G(t;U)替换;对于问题 (22) F(t;U)=U-(I-Δ)-1{D-1G(t;U)+U}=0. (23) 其中σn是奇数.由引理1可得 (24) (25) 由定理2和定理3知,存在一个正常数b使得,对任意的0≤t≤1,系统(22)的正解满足b-1 deg(F(1;·),0,B(b))=deg(F(0;·),0,B(b)). (26) deg(F(1;·),0,B(b))= 与式(26)矛盾,则定理结论成立.证毕. 注当k=2,d=1.5,c=6,r=1.28,m=3时条件(5),(8),(19)及H>d+1可同时成立. 应用反应扩散方程理论、单调动力系统理论、分歧理论、拓扑度理论研究了带有扩散的捕食模型,讨论了正常数解的先验估计及其稳定性、共存解的存在性以及参数对解的影响.主要证明了当种群扩散率d3≥ρ时,捕食模型至少存在一个非常数正解.
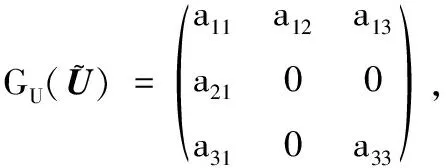
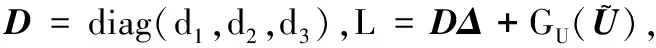
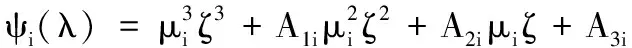
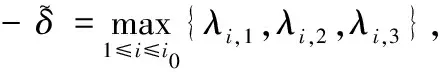
2 正常数解的估计
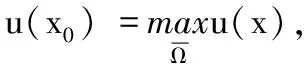

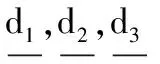
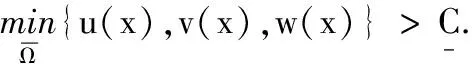
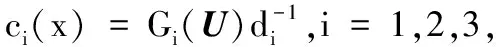
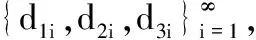
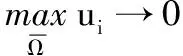

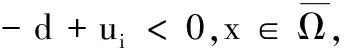
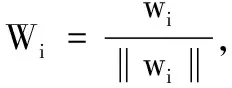
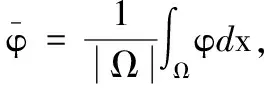
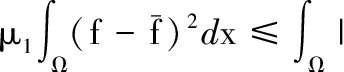
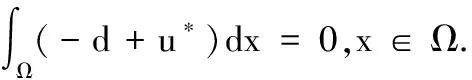
3 非常数正解的存在性
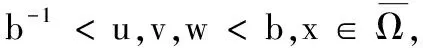
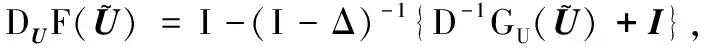
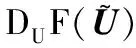
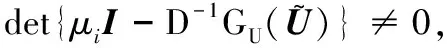
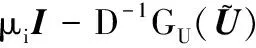

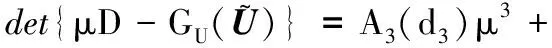
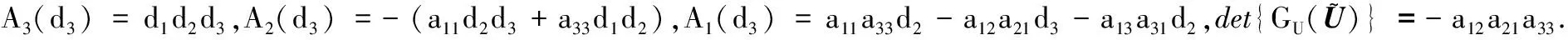
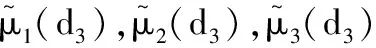
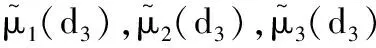
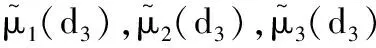
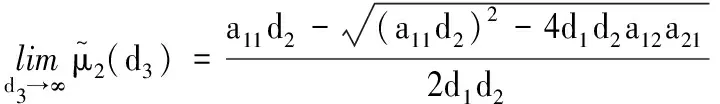
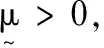
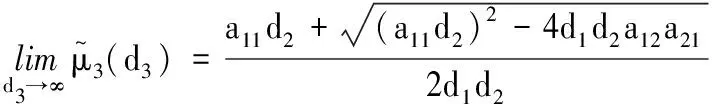
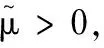
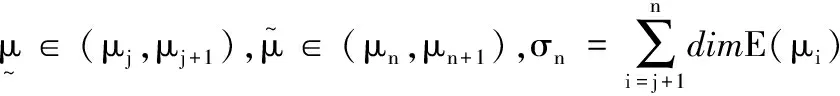
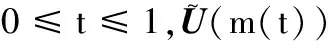
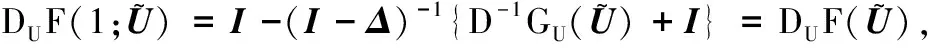
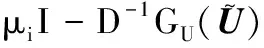
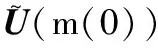
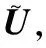
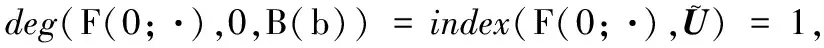
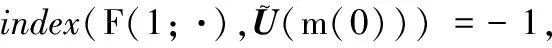
4 结束语
