一类富营养湖泊中藻类的状态反馈控制模型
2015-08-08傅金波郭红建
傅金波,郭红建
(1. 福建师范大学 闽南科技学院, 福建 泉州 362332;2.信阳师范学院 数学与信息科学学院,河南 信阳 464000)
0 引言
湖泊富营养化已成为淡水水环境面临的主要水污染问题之一.造成湖泊富营养的因素有很多,如工业污水和城镇生活污水大量排放、水产养殖过量投放饲料等.这些污水和未被利用的含有大量氮磷的营养物,随地表径流和雨水冲刷进入到湖泊水体.水体中氮磷等的长期堆积是水体富营养的主要原因.
水体富营养为藻类的生长和繁殖提供了物质基础,在适宜的条件(如气温等)下,藻类快速和大量繁殖,甚至形成“水华”.由于藻类的过度繁殖,大量消耗水中的氧气,使得其他生物的生存环境下降.另外,还有一些藻类会释放一些毒素.总之,水体富营养造成的藻类大量繁殖甚至水华,使湖泊水质变得污浊,透明度降低,水生生物大量死亡,严重破坏湖泊生态系统平衡.关于水体富营养化及其危害的研究已有很多文献报道[1-3].
为了防止湖泊中的藻类暴发成水华,人们采取了很多措施,如投放鱼类、物理或化学除藻等措施,本文利用状态脉冲微分方程描述一类对藻类的状态反馈控制问题.当藻类的数量没有达到一定阈值时,对其不进行控制,一旦其数量达到某个阈值,则采取一定的控制措施,使得其数量减少(这里主要考虑的是成比例减少).基于此思想,具有状态反馈脉冲控制的藻类-营养生态系统的数学模型可写为:
(1)
其中:s(t)表示t时刻水体中营养成分的浓度,x(t)表示t时刻藻类的密度,S0表示水体中营养成分的输入量,u为流失率,r为藻类的内禀生长率,bs+K为容纳量,h为藻类数量的临界控制值,p为去除率.
关于具有状态反馈控制的生态系统数学模型已有许多结果,参见文献[4-11]等.文献[8]给出了阶k周期解的定义及基本的研究方法,下面利用文献[6]和[8]的思想讨论系统(1)阶1周期解的存在性和稳定性.首先给出无脉冲作用的情况下,系统(1)的定性和稳定性结果.
1 无脉冲作用系统的稳定性
无脉冲作用下的系统(1)可写为
(2)
系统(2)有2个平衡点,E0=(S0/u,0),E=(s1,x1),其中,
系统(2)的雅可比矩阵为
易知点E0=(S0/u,0)是不稳定的鞍点.
对于点E=(s1,x1),可得
从而可知特征方程为:λ2+pλ+q=0,其中
易知特征方程的两个根均小于0,进而可知E=(s1,x1)是稳定的.再由
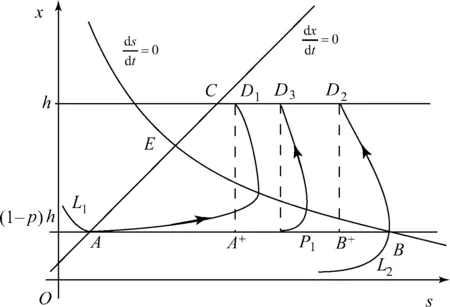
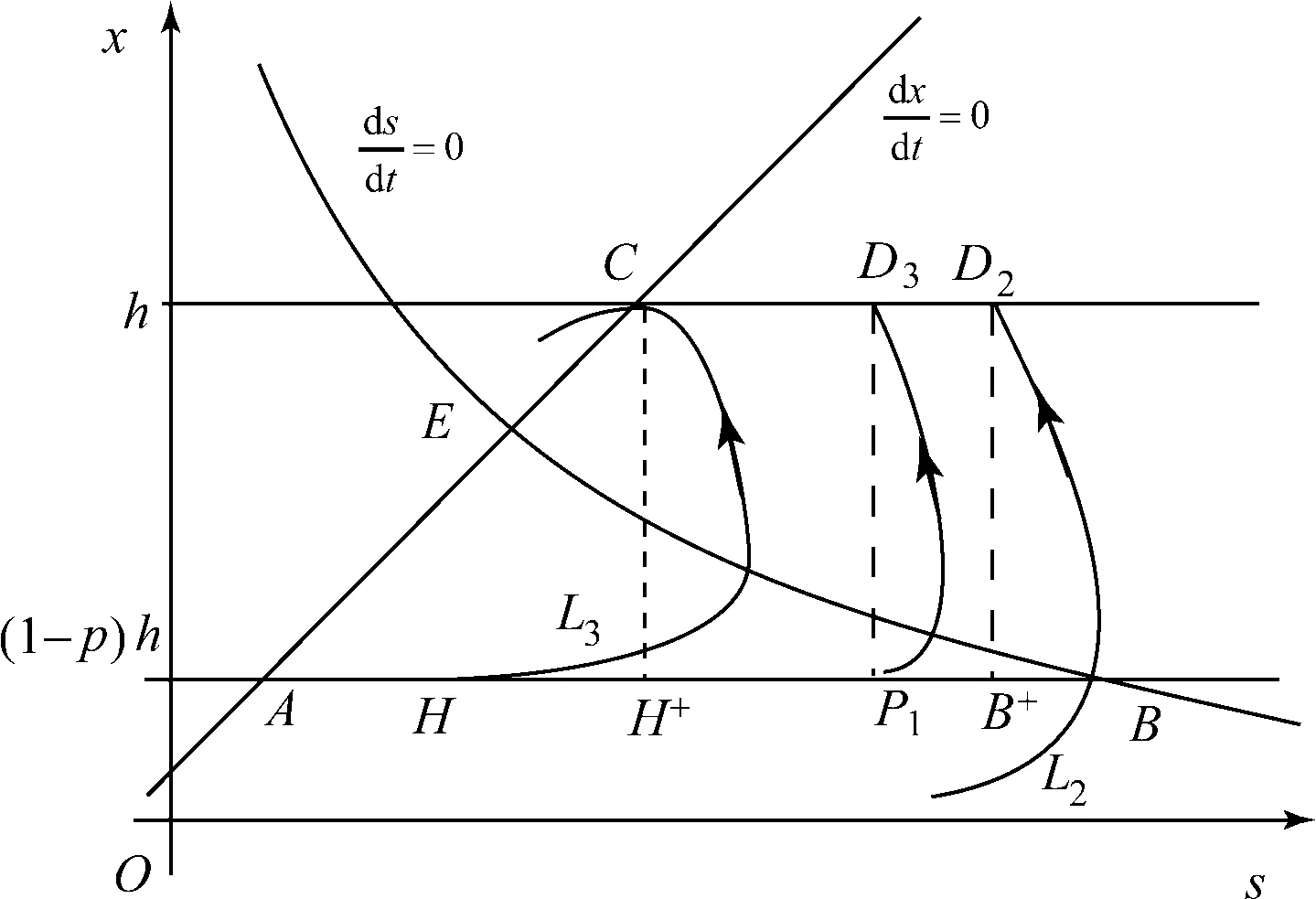
可知,当r1 从而有定理1. 定理1 当r1 定理2 系统(2)的解是最终有界的. 综上所述,存在由x=0,y=0,Γ1,Γ2所围成的区域Ω,即对任意初始值(s(t0),x(t0)),存在T>0,当t>T,有(x(t),y(t))∈Ω,即系统(2)的解是最终有界的.证毕. 定理3 当r1 由Bendixson-Dulac定理,在E=(s1,x1)的周围不存在闭轨.证毕. 定理4 当r1 定义2 设P1(s,(1-p)h)∈N,存在T1,使f(P1,T1)=Q1∈M,脉冲映射I(Q1)=I(f(P1,T1))=P1∈N,称f(P1,T1)为系统(1)的阶1周期解. 由微分方程定性理论可得,存在唯一的系统轨线L1与x=(1-p)h相切于A点. 下面分别讨论脉冲集x=h,像集x=(1-p)h与正平衡点E=(s1,x1)的不同位置关系时,系统(1)阶1周期解的存在性. 记系统轨线L1与x=h交于点D1(sD1,h),易知sA 定理5 如果r1 图1 当h≤x1时阶1周期解存在性示意图 a) 若系统轨线L1,与脉冲集x=h交于点D1(sD1,h),如图2所示,类似定理1的讨论可知,系统(1)存在阶1周期解. 图2 当h≤x1,yA 图3 当时阶1周期解存在性示意图 图4 当时阶1周期解不存在性示意图 定理6 如果r1 对于(1-p)h>x1的情况,实际生物意义和现实意义不大,这里不再考虑. 下面利用类Poincaré准则[6]证明系统阶1周期解的轨道渐近稳定性. 定理8 设Γ0是系统(1)过点(ξ0,h)的阶1周期解,如果μ2<1,则Γ0是轨道稳定的且具有渐近相图的性质,其中 证明设(ξ(t),η(t))是系统(1)过点(ξ0,h)的阶1周期解Γ0,令 α(s,x)=0,β(s,x)=-px, φ(s,x)=x-h,(ξ(T),η(T))=(ξ0,h), (ξ(T+),η(T+))=(ξ0,(1-p)h), 则由文献[6]可计算得到 从而 进而 由文献[6]可知,当μ2<1时,阶1周期轨道(ξ(t),η(t))是轨道稳定的,且具有渐近相图的性质.证毕. 研究了一类具有状态脉冲控制的藻类-营养生态系统的数学模型,讨论并得到了阶1周期解的存在性和稳定性.如果人们对藻类的控制阈值h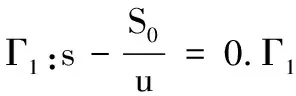
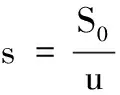
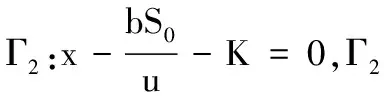
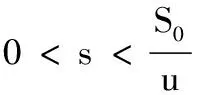
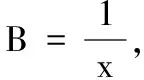
2 阶1周期解的存在性和稳定性
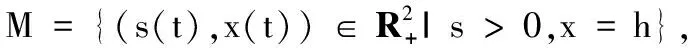
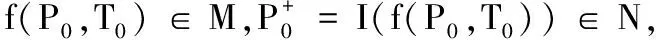
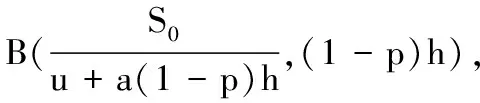
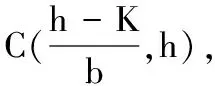
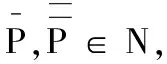
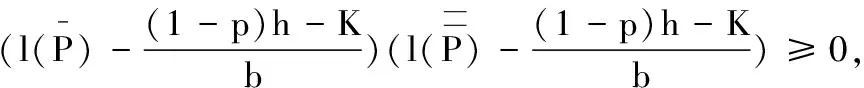
2.1 情况I:h≤x1
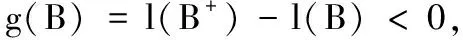

2.2 情况II:(1-p)h
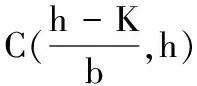

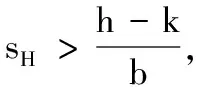


3 结论
