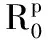具有抗性发展和轮换使用杀虫剂的综合害虫治理模型的动力学性质

韩静光,刘 兵,王洪娇

(1.辽宁师范大学 数学学院, 辽宁 大连 116029;2.鞍山师范学院 数学与信息科学学院, 辽宁 鞍山 114007)

0 引言

在农业生产中,为了大力发展农业生产，需要有效地控制农业害虫.杀虫剂以其易于操作、见效快且经济实惠等特点,被人们视为控制害虫的主要手段之一.然而,杀虫剂的频繁使用,不仅引发环境污染、农药残留等问题,更促使害虫对杀虫剂产生抗性,从而使其有效性降低.目前,很多人利用脉冲微分方程研究化学控制下害虫种群的动力学性质[1-7],但很少有人将害虫对杀虫剂的抗性考虑到模型中.文献[4]将抗性发展引入单种群脉冲喷洒杀虫剂的害虫控制模型,并通过数学模型研究抗性的发展如何影响害虫种群的动力学性质.本文在此文献基础上将抗性发展及周期性轮换杀虫剂策略引入综合害虫治理模型即周期喷洒杀虫剂和投放天敌的脉冲模型中,并分析该模型的动力学性质及其生物意义.

1 模型建立

本文在不同的固定时刻分别喷洒杀虫剂和释放天敌,基于文献[5]建立如下模型:

(1)

其中：x(t)和y(t)分别表示害虫和天敌在t时刻的种群数量；r,a,λ,μ,h均为正常数；n∈Z+={1,2,…};r为害虫种群的内禀增长率；K为环境容纳量；a为捕食率；λ为转化率；h为处理时间；0<δ<1为t=nT时刻喷洒杀虫剂后天敌的残存率；q(nT)为t=nT时刻喷洒杀虫剂后害虫的残存率函数；μ>0为t=(n+l-1)T时刻释放天敌的数量.这里将抗性发展引入害虫治理模型，假设同一种杀虫剂喷洒一段时间后,害虫种群会产生抗药性,因此周期性轮换使用杀虫剂，此时每种杀虫剂的残存率函数q(t)是时间t的变量,满足[6-7]

(2)

其中：τp为轮换杀虫剂的周期,这里我们假设每种杀虫剂使用p次且具有相同的初始有效性；T为喷洒杀虫剂周期,且设τp=pT；q0为首次喷洒杀虫剂后害虫的残存率；α为害虫残存率的内禀增长率.

2 模型(1)的动力学性质

下面系统(3)对于系统(1)动力学性质的分析起着重要的作用，

(3)

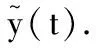
证明在任意脉冲区间((n-1)T,nT],当t∈((n-1)T,(n+l-1)T],对系统(3)的第一个方程求积分得

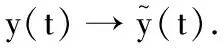
y(t)=y((n-1)T+)e-d(t-(n-1)T),

在t=(n+l-1)T时释放天敌，

y((n+l-1)T+)=y((n-1)T+)e-dlT+μ.

当t∈((n+l-1)T,nT]时，

y(t)=y((n+l-1)T+)e-d(t-(n+l-1)T),

在t=nT时喷洒杀虫剂，

y(nT+)=δy((n-1)T+)e-dT+δμe-d(1-l)T.

令y((n-1)T+)=yn-1,由上式可得差分方程,

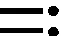
(4)

其中：φ=δe-dT,Φ=δμe-d(1-l)T.

证毕.

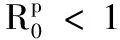
(5)

这里qi=q(iT)为每种杀虫剂第i+1次喷洒杀虫剂的残存率,i=0,1,2,…,p-1；

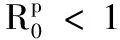
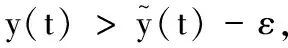
(6)

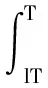
对于t∈(mτP,(m+1)τP],根据脉冲微分方程的比较定理,有

x((m+1)τp)≤qp-1x((p-1)T+

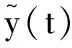
注意到qp=q0,从而有

aε)-ay*e-dt)dt+

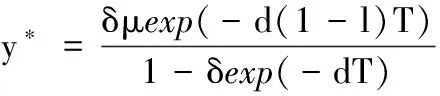
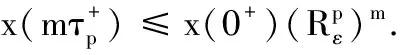
考虑系统(3)和下面脉冲微分方程:

(7)

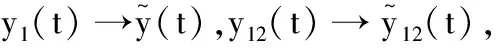
是系统(7)全局渐近稳定的周期解.

令ε→0,当t充分大时有

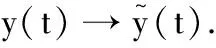
注1 关于喷洒杀虫剂后害虫残存率函数qk的值,可由求解系统(2)得到.由系统(2)可得

其中：q0为每种杀虫剂首次喷洒后害虫的残存率,则第二次喷洒杀虫剂后害虫残存率为

第三次喷洒杀虫剂后害虫残存率为

则第p次喷洒杀虫剂后害虫残存率为

qp-1=q((p-1)T)=

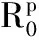
(8)

3 结论