基于可变客流的接运公交网络优化

王志美，张星臣，陈军华，盖振州

（北京交通大学交通运输学院，北京100044）

基于可变客流的接运公交网络优化

王志美*，张星臣，陈军华，盖振州

（北京交通大学交通运输学院，北京100044）

在充分考虑目的地非地铁站的变动客流和搭乘固定公交的既有客流基础上，基于多对多客流模式，以管理者、出行者和社会运营费用的总费用最小为目标，构建接运公交线路的优化模型.模型考虑了原本私家车出行客流和固定公交出行客流选择接运公交出行的可能性，应用Logit模型进行流量分配，并采用遗传算法对问题求解，获得了最优的接运公交网络，变动客流在接运公交网络中的第一公交站和换乘的地铁站.研究结果表明，接运公交线路方案与其占全程广义出行费用的比例密切相关，故有必要将其从全程视角进行优化.

城市交通；接运公交；遗传算法；可变客流；固定公交

1 引言

随着城市规模和人口数量的不断扩大和增长，交通拥堵、环境污染等问题越来越严重.如何将私家车客流吸引到公共交通（包括公交和地铁网络）已成为关注热点.而在平峰时段，固定公交的开行间隔较长，造成了较长的等待时间.与地铁线路衔接的接运公交不仅弥补固定公交的上述缺陷，而且能节省运营费用.因而，接运公交线路优化问题成为当前国内外学者的研究热点，主要基于解析方法[1,2]和网络优化方法[3-5]进行研究.

服务于地铁线路的接运公交设计问题主要从单一类型交通模式和多种类型交通模式的角度出发.单一类型交通模式的接运公交设计问题最早被Kuah等[3]和Maritins等[4]提出.kuah等以乘客和管理者视角的总费用最小为目标，优化与铁路线路相接运的公交线路结构和运行频率；Martins等对Kuah等提出的问题进行扩展，建立了两阶段模型且设计了更好的优化算法对问题进行优化. Wirasinghe等[5]通过构建数学模型解决影响地铁与公交系统协调问题，并分析了地铁站站距、接运公交服务区域及列车开行频度3个关键因素对优化结果的影响.由于该问题是NP难题，难以在现实网络上求解.而Kuan等[6,7]通过启发式或混合算法的角度对问题进行研究.上述研究均假定客流的发到站为公交站和铁路/地铁站，且客流量为定量，而本文研究认为：

（1）部分目的地非地铁站的客流为变动客流，其是否选择接运公交和地铁出行，取决于公共交通和私家车广义出行成本的权衡.

（2）乘客可选择的第一公交站为一个备选集，而非指定站.乘客需在权衡走行距离和等待时间的基础上选择合适的第一公交站.

（3）也考虑了原由固定公交线路运送的客流被接运公交吸引的可能性.

多种类型的交通模式包括低成本小运量的接运公交，出租车及私家车等.着眼于多种类型交通模式接运网络设计问题的研究主要有Shariat等[8]和Ohaymany等[9].他们也是假定客流的出发和到达站已知，应用蚁群算法求解多种模式并存的接运网络优化问题.本文研究同多种类型交通模式接运公交网络研究，考虑变动公交，固定公交和私家车共存情形，但认为客流可选择的换乘地铁站不是固定的，而是随接运公交网络的变化而变化，取决于优化的接运公交方案和其将要搭乘的第一公交站方案.

综上，本研究考虑了多种类型交通模式并存情形，在不确定的公交站与地铁站间的OD流基础上，构建数学模型和应用遗传算法求解接运公交优化方案.

2 问题描述及模型构建

2.1 问题描述

本节以图1为例对问题进行阐述.图1中共有私家车、固定公交、接运公交和地铁四种交通方式，其中，固定公交和接运公交均与地铁网络衔接.已知区域1为私家车和固定公交客流的产生域，区域2为私家车客流的吸引域，也为市中心.在这样的网络中，私家车客流和固定公交客流均多了一种出行选择，即搭乘接运公交—地铁（—接运公交）的方式出行.本文要解决的问题是在哪些线路上建立接运公交，在哪些线路上取消固定公交，使得原本私家车出行和固定公交出行客流出行成本，运营公司的管理成本和社会成本之和最小.

图1 乘客出行链示意图Fig.1 Passenger routing chain

2.2 模型假设

（1）每条接运线路仅能衔接一个铁路站，且其经过的公交站均停车；

（2）每个公交车站最多能停靠一条接运线路；

（3）乘客只选择与出发地相邻的其中一个公交站；

（4）从出发地到地铁站区域，假定客流不存在换乘；

（5）每个接运线路有最远距离、最大停站次数、最长时间、最大能力等约束；

（6）设初始存在两种类型的客流，私家车和固定公交出行客流，他们的备选出行方案均由接运公交替代一部分或全部行程.

2.3 模型构建

（1）集合.

Q,Q′——私家车和固定公交客流需求集合, q∈Q，q′∈Q′；

u(q)——编号为q的OD对客流量；

p(q),d(q)——分别为第q支OD流的接客点(出发地)和送客点(目的地)；

o(r),d(r)——分别为线路r的始发站和终到站；N1,

N2——分别为区域1和区域2中的公交站集合；

N3——地铁站集合；

R1,R2——分别为区域1和区域2可能的接运公交线路集合；

R3——铁路线路上服务的列车弧；

R4——区域1的固定公交线路集合；

adj(p(q))——与接客点p(q)相邻的所有公交站集合；

adj(d(q))——与目的地d(q)相邻的所有公交站集合.

（2）输入参数和变量.

W——网络中接运公交的最大数量；

fmax——每个接运公交的最大开行频度；

smax——每个接运公交的最多停站次数；

kcap——每个接运公交的能力；

Nr——第r个线路能分配的最大车辆数；

Lmax——每个接运公交的最长里程；

lr——接运公交r的运行距离；

tir——线路r上i节点到线路终到站的时间；

tr——线路r总消耗时间.

（3）决策变量.

Yr——如果接运线路r（属于区域1,2,3）在i站停靠，则取值为1，否则取值为0；

Xq——如果第q支客流被第r条接运线路运送，则取值为1，否则取值为0；

δr——如果第r条接运线路开行，则取值为1，否则取值为0；

πP(q),i——如果与第q支客流出发点p(q)相邻的公交站i为第一出发站，则取值为1，否则为0；

fr——接运公交r的开行频度.

（4）接运公交客流需求.

①私家车客流选择接运公交的概率.

原有私家车出行的乘客选择接运公交出行的概率表示为

式中ubqus是在“出发地→公交站→地铁站→公交站→目的地”这一出行链上的广义费用，表示为

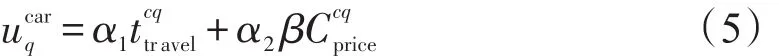
②固定公交客流选择接运公交的概率.

原固定公交出行的乘客选择接运公交方式出行概率表示为

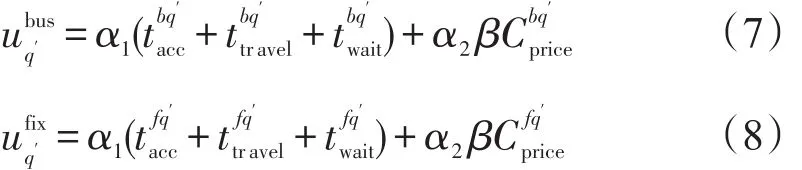
（5）目标函数.

目标函数中的费用包括3个方面：接运公交和固定公交的管理费用、用户费用和社会费用，γ1,γ2,γ3为上述3种费用的权重.

①管理费用.

接运公交和固定公交的管理费用可被描述为正比于车辆运行距离，可表示为

②用户费用.

乘客选择私家车、接运公交和固定公交出行所耗费的总费用表示为

③社会成本.

私家车出行和乘坐接运公交出行所消耗的社会资源不同，社会成本以乘客消耗的总资源最小为目标，表示为

（6）约束条件.

①OD客流的约束.

式（13）保证了任意的q在区域1内有连续的出行链.若某个公交站属于与出发地相邻的公交站集合，且被选为第一公交站，则该OD必须从该公交站搭乘一条公交线路到达地铁站；式（14）保证了与“地铁站至终到站”这一行程链相关的公交线路的接续.

②客流与接运公交线路的关系约束.

式（15）保证了客流能够选择公共交通出行的前提是运行对应的接运公交线路.

③接运公交线路的其他约束条件.

式（16）～式（21）分别为线路最大开行频度、最大车辆数约束、最长运送时间、运送距离、最大运送能力和最多停站次数约束.

3 求解方法

该问题是路径生成问题的扩展，路径优化问题已经证实可被元启发式方法求解，取得较好效果.本文以应用较为广泛的遗传算法为求解方法，用以确定接运线路的起点、终点及沿途停靠站，线路的开行频度，客流分配方案等.具体求解过程如图2所示.

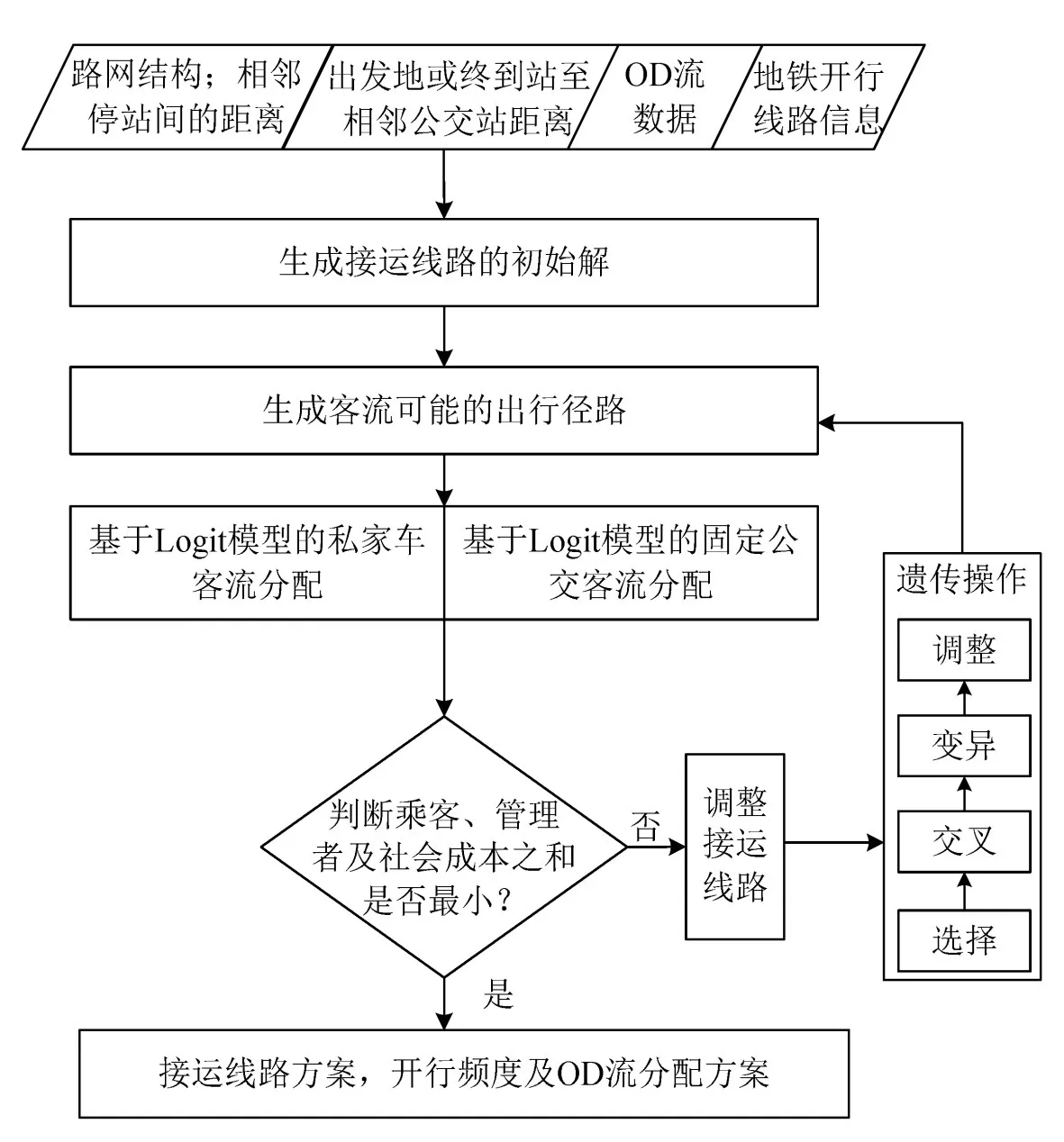
图2 算法流程图Fig.2 The program flow chart of GA

本问题的一个解由若干组接运线路组成，每组线路由线路开行频度及线路的停靠站构成，如图3所示.为简化问题，这里用每条线路分配的车辆数替代开行频度.开行频度和车辆数的关系可表示为

图3 染色体解码方式图Fig.3 Chromosome representation of problem

式中Vn表示分配到线路n上的车辆数；Tn表示线路n一个周转时长.

该问题初始解的生成，适应值的表示方式及交叉变异操作可参照文献[6].本文在配流处理上与文献[6]有所不同，采取的策略为：

（1）将与居民住地相邻公交站点按照走行距离从近到远的顺序排列，作为乘客选择其出发站及走行时间的依据.

（2）利用Logit模型，与备选的私家车出行及固定公交线路出行方案进行合理分配.在配流过程中，假定对应线路上的能力充足；分配结束后，将能力约束函数以惩罚项的形式计算入适应值函数中.

4 案例分析

假设平峰时段客流由家出发，去往目的地，目的地在市中心.市中心区域接运地铁线路的固定公交线路开行频度与高峰时段相同，即认为每个地铁站运送到目的地的出行时间为常数.

以图4为例，已知站1～7为接客区域的公交站点，站8～10为铁路站点，站11～13为到达区域（市中心）的公交站点，连线上的数字为站间距.各地铁站至到达域公交站点的运送时间和费用如表1所示；原乘坐私家车出行的客流数据、行驶时间、费用等如表2所示.同时，假定接客区当前仅有一条固定公交线路5→4→3→8，在该线路上从站5、4、3分别去往站8的客流量为25，30，33人.固定公交的平均运行速度设为20 km/h.

图4 案例示意图Fig.4 A network for case study

表1 铁路站至各到达站的运送时间和费用Table 1Travel cost and time from stations to destination stops

表2 原自驾出行的客流量、行驶时间和费用参数Table 2The volume of passenger,travel time and cost for each private car OD demand

4.1 相关参数定义及求解效果分析

在遗传算法里，染色体种群的规模设置为50，交叉概率、变异概率分别取0.6、0.2，染色体集合的最大规模设为100.当算法进化迭代次数达到500次，或染色体集合在连续迭代的100次计算中维持不变时，停止计算并认为算法达到收敛.接运公交线路相关的费用参数参照相关文献，取值如表3所示.

表3 费用参数取值Table 3The value of parameters

以上述数据作为模型的输入参数，经遗传算法求解，得到优化方案.遗传算法求解的效果如图5所示.

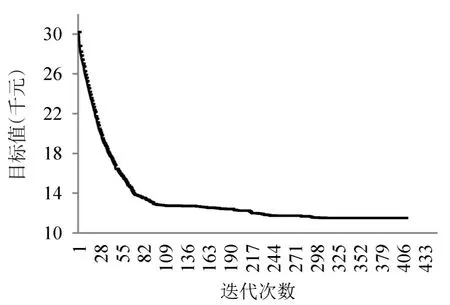
图5 遗传算法进化曲线Fig.5 Evolution curve of genetic algorithm

由图5可以看出，在总步数不超过500次，而近似最优解的值超过100次未改变，算法终止.个体目标值随着遗传代数的增加逐步下降并趋于稳定，表明本文给出的遗传算法具有较好的收敛性，总可以得到一个近似最优解.

4.2 方案分析

经过优化计算，得到的最优接运公交线路及由每条接运公交线路运送的客流信息如表4和表5所示.

（1）接运公交最优的开行路线.

表4 最优的开行路线Table 4The optimal feeder lines

（2）乘坐接运公交的客流信息.

表5 乘客的出行方案Table 5Routing strategy for each OD demand

由表4可知，当前网络上共开行了3条线路，保证了路网中的客流均能从出发站运送到地铁站.由表5可知，出发地序号为6的客流从公交站7始发，出发地序号为7的客流从公交站6始发.客流运送方案由出发地至其相邻公交站的距离以及接运线路方案共同确定的.

（3）选择私家车出行的客流比例.

在客流的分配方案已知的基础上，进一步统计每支客流中仍然选择私家车出行的比例，如表6所示.

表6 现有方案下私家车的出行比Table 6A proportional value for OD demands traveling by private car based on current feed bus strategy

由表6可知，有7支OD流不到20%的流量选择私家车出行；有4支OD流的私家车出行比例在20%～30%之间；有2支OD流超出30%的乘客选择私家车出行；序号为9的OD流仍选择私家车出行比例较高.

（4）仍然选择固定公交出行的客流比例.

依据当前的接运公交网络可知，原乘坐固定公交的OD流3-8，4-8，5-8均多了一种出行选择——乘坐接运公交.其在接运公交上所选择的线路如表7所示.依据两种出行方式的广义出行费用，确定了分配到接运公交上的流量比例.配流结果表明，接运公交的开行，也会对固定公交流量起到分流作用.因而，有必要将固定公交线路方案考虑在内，制定经济可行的接运线路.

表7 原固定公交客流转移路线及流量信息Table 7The alternative route and proportional value for demands original on fixed bus

4.3 灵敏度分析

由于本文从乘客全程的出行广义费用视角出发，研究接运公交方案.通过变化“地铁→到达站”这段行程的广义出行费用（从减少20%到增加20%），发掘其对接运公交方案的开行辆数及吸引的客流量产生的影响，结果如图6所示.

图6 后半程费用变化与接运公交开行方案的关系Fig.6 The relationship between the last part of journey and feeder bus strategy

由图6可知，接运公交的开行辆数和吸引的客流量比例随后半程费用的增加而减少.由于每辆接运公交容量一定，故其开行辆数与后半程广义费用非线性化增长.由此揭示接运公交的吸引客流量与其占全程出行费用比例相关，应将其作为全程广义出行费用的一部分进行优化方案.

5 研究结论

本文在多对多客流模式前提下，以目的地非地铁站的私家车客流和搭乘固定公交的既有客流为模型的研究对象，构建了接运公交网络线路优化模型，使得管理者、出行者及社会角度的总费用最小，优化出了变动客流的接运公交网络第一公交站和换乘的地铁站.模型考虑了原本私家车和固定公交客流选择接运公交出行的可能性，采用Logit模型进行流量分配，使得接运公交方案与乘客的出行选择交互作用.采用了遗传算法对问题求解，方案结果表明，接运公交的开行可吸引多数的私家车客流到公交系统，且接运公交出行所消耗的广义费用占全程的比例影响着乘客的出行抉择；固定公交线路客流分流到接运公交的比例与方案相关.

[1]Xiong J,Guan W,Song L Y,et al.Optimal routing design of a community shuttle formetro stations[J]. Journal of Transportation Engineering,2013,139(12): 1211-1223.

[2]Chien S I,Spasovic L N,Elefsiniotis S S,et al. Evaluation of feeder bus systems with probabilistic timevarying demands and nonadditive time costs[J].Transit: Bus Transit and Maintenance,Paratransit,and New Technology,2001,(1760):47-55.

[3]Kuah G K,Perl J.Optimization of feeder bus routes andbus-stopspacing[J].JournalofTransportation Engineering-Asce,1988,114(3):341-354.

[4]Martins C L,Pato M V.Search strategies for the feeder bus network design problem[J].European journal of operational research,1998,106(2-3):425-440.

[5]Wirasinghe S C,Hurdle V F,Newell G F.Optimal parametersforacoordinated rail and bus transit system[J].Transportation Science,1977,11(4):359-374.

[6]Kuan S N,Ong H L,Ng K M.Solving the feeder bus network design problem by genetic algorithms and ant colonyoptimization[J].AdvancesinEngineering Software,2006,37(6):351-359.

[7]Kuan S N,Ong H L,Ng K M.Applying metaheuristics to feeder bus network design problem[J].Asia-Pacific Journal of Operational Research,2004,21(4):543-560. [8]Shariat Mohaymany A,Gholami A.Multimodal feeder networkdesignproblem:antcolonyoptimization approach[J].JournalofTransportationEngineering, 2010,136(4):323-331.

[9]TahooriniaM M,Mohaymany A S,GholamiA. Designing a multimodal feeder network by covering stops with different modes[J].Canadian Journal of Civil Engineering,2014,41(1):87-96(10).

Feeder Bus Network Design Based on Variable Demand

WANG Zhi-mei,ZHANG Xing-chen,CHEN Jun-hua，GAI Zhen-zhou
(School of Traffic and Transportation,Beijing Jiaotong University,Beijing 100044,China)

This study takes account of the private car demands whose destinations are not subway station and the demands taking the fixed bus lines originally,develops a feeder bus network optimal model with the minimum cost of passengers,operators and social for many-to-many travel demand.Logit model is applied to redirect private car demand between private car and feeder bus line,fixed bus line demand between feeder bus and fixed bus line.A genetic algorithm is developed to solve the problem.The results show that the model constructed in this paper and the applied genetic algorithm can obtain optimal feeder bus lines,the first bus station and transfer subway station for originally private car demand.The solution result shows that the feeder bus line strategies have a close relationship with the percentage of the whole traveling chain costs.

urban traffic;feeder bus;genetic algorithm;variable demand;fixed bus

1009-6744（2015）05-0128-08

U268.6

A

2015-05-12

2015-08-19录用日期：2015-08-27

国家自然基金资助项目（U1361114）；国家自然基金青年基金项目（71401006）；北京交通大学基本科研业务项目（2015JBM059）.

王志美（1984-），河南民权人，博士后. ＊

wzm_sxhd@163.com