高铁快递与传统快递合作定价的Stackelberg博弈模型

段华薇，严余松

（1.西南交通大学交通运输与物流学院，成都610031；2.西南财经大学天府学院，成都610081）

高铁快递与传统快递合作定价的Stackelberg博弈模型

段华薇1,2，严余松*1

（1.西南交通大学交通运输与物流学院，成都610031；2.西南财经大学天府学院，成都610081）

为得出传统快递与高铁快递合作的最优定价策略，分析主导权及市场需求波动对其影响，根据双方构成供应链的特点，基于两种随机市场需求函数分别构建了高铁快递和传统快递主导下的Stackelberg博弈模型，分别得到高铁快递的最优协议运价策略和传统快递的最优协议运量和市场运价策略，通过算例验证了模型的有效性.得到结论，决策权的分散导致总利润降低；高铁快递掌握主导权可以增加自身利润和供应链总利润；传统快递在合作中获得利润大于高铁快递获得利润，但不一定大于其非合作时的利润；市场需求波动增大，会导致双方的利润大幅降低.

交通运输经济；最优定价策略；Stackelberg博弈；高铁快递；传统快递；随机需求

1 引言

2014年4月1日起，中铁快运公司在20个城市开办高铁快递业务，我国高铁快递正式面世.高铁快递作为新兴的快递运输形式，其速度相比公路快递更快，成本相比航空快递更低，所受的影响因素较少，准点率较高，时效性较强.但其只在500～1000 km运距范围内具有竞争力，而且目前我国铁路运输企业“门到门”服务能力及揽货能力都还较弱，快递客户资源匮乏.现阶段只有20个城市开办高铁快递业务，其承接的业务量有限.另一方面，传统快递企业的市场占有率很高，拥有成熟的配送网络及丰富的快递客户资源，但其运输方式较为单一，依靠铁路等形式进行运输的还不足5%，存在结构性运力不足问题.可见，高铁快递和传统快递进行合作有利于双方自身的发展和我国快递行业的可持续发展.在合作过程中，高铁运输企业承接高铁快递业务的定价问题又是双方关注的核心问题，因此，有必要对双方合作定价问题进行理论研究.当前已有文献[1，2]针对高铁快递发展问题进行了定性研究，但未涉及双方合作的定价问题.

考虑主导权的Stackelberg博弈模型的研究为本文研究提供了思路.Gerchak[3]和Dong[4]将制造商主导下的Stackelberg博弈模型应用到定价问题研究中.Geylani[5]研究了由零售商决定批发价格时，生产商的联合促销和广告决策.国内学者也广泛应用Stackelberg模型对定价问题进行了研究，文献[6，7]分别基于Stackdberg博弈模型研究了航空货运期权定价问题、包含超售因素的机票动态定价模型.但在上述研究中，都没有考虑市场需求随机性.

关于随机市场需求函数，Mills和Karlin分别构建了期望需求函数与随机变量相加和相乘构成的随机需求函数.Petruzzi[8]将这两种随机市场需求函数应用到报童模型中，得到了两种需求函数下供应商和零售商的最优策略.但上述研究都没有考虑供应链主导权.虽然冯芬玲[9]在研究中假设铁路货运需求满足加性需求，但还没有针对高铁快递市场随机需求函数的研究.

同时考虑主导权和随机市场需求的研究：Jiang[10]针对供应商之间存在竞争的分布决策组装系统，研究了乘性需求下的供应商主导Stackelberg博弈模型，但没考虑零售商主导的情况.Shi[11]基于四种随机市场需求函数，分别构建了制造商和零售商主导的Stackelberg博弈模型和两者同时决策的NASH博弈模型，但其利润函数并不适合高铁快递和传统快递所构成的供应链.

综上所述，当前亟待对高铁快递和传统快递合作定价策略进行定量研究，但同时考虑主导权和随机需求的Stackdberg博弈模型研究不多，现有模型也不适用于双方合作定价问题.因此，本文从供应链管理角度对双方合作的特点进行分析，构建同时考虑主导权和随机需求的双方合作定价的Stackelberg博弈模型，得出双方合作的最优定价策略，并通过算例分析主导权及市场需求波动对其影响.

2 问题描述

将双方合作过程具体描述为传统快递根据快递市场需求（D(p,ε)）按市场价格（p）承揽零散客户的高铁快递业务，并与高铁运输企业以较优惠的协议运价（w）签订协议运量（q）的承运协议，由高铁快递完成相关的快递运输（高铁快递运输成本为cr）.值得注意的是，当协议运量大于市场需求时，不存在库存成本；当协议运量小于市场需求时，由传统快递自己完成协议运量不足的运输任务（传统快递运输成本为cc），如图1所示.

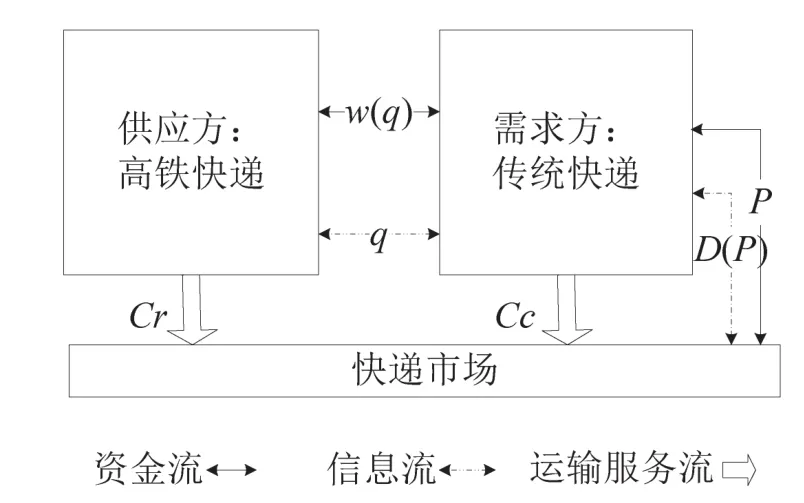
图1 高铁快递与传统快递合作示意图Fig.1 Schematic diagram for the cooperation of CRHexpress and traditional express

可将双方的合作视为一个传统快递同时对协议运量和市场运价进行决策，高铁快递对批发价格进行决策的供应链，该供应链是分布决策的、双方都可能具有主导权，且快递市场的需求是随机变化的.而双方合作定价确定的过程实质就是双方以自身利益最大化为目标进行非合作博弈的过程，且该博弈存在行动的先后顺序，属于动态博弈.

3 基本假设、符号定义及相关函数

3.1 基本假设

假设1仅考虑一家高铁快递企业与一家传统快递企业的合作，两者都是理性的.

假设2双方的博弈属于完美信息博弈.

假设3高铁快递和传统快递首先根据主导权分别对协议运价和市场运价进行决策，传统快递最后对协议运量进行决策.

3.2 变量定义

表1对本文中所用到的变量进行具体定义.

表1 变量定义表Table 1Variable definitions

3.3 随机需求函数

文献[12]定义了两种随机需求函数.

（1）加性随机需求函数.

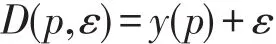
式中y(p)=a-bp(a＞0,b＞0)；ε是取值范围为[A,B]的随机变量，其分布函数为F(∙)，密度函数为f(∙)，且均值为μ，方差为σ.

（2）乘性随机需求函数.

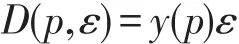
式中y(p)=ap-b(a＞0,b＞1).

对于品牌商品由于市场需求相对稳定，应采用加性随机需求函数；而对于新产品由于价格的变化会引起市场需求规模较大变化，应采用乘性随机需求函数[12].高铁快递是一种新的快递运输形式，属于新商品；但其本质上属于铁路运输，安全性、稳定性非常突出，又具有“品牌商品”的属性.因此，本文分别基于这两种随机需求函数进行研究.

3.4 合作双方利润函数

传统快递利润函数表示为

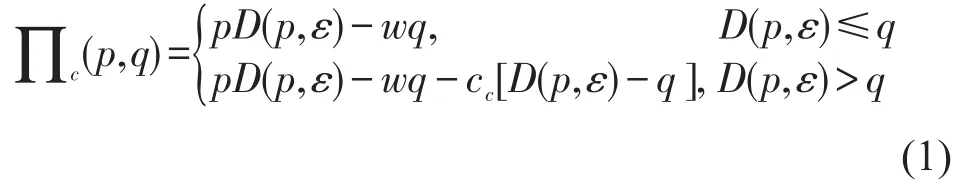
根据双方合作实际，利润函数未考虑库存成本和需求不满足时的惩罚成本.

高铁快递的利润函数不受快递随机需求变化的影响，表示为

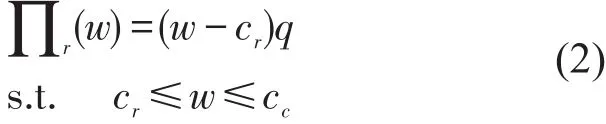
双方都是理性的，合作的基础为双方都有获利，故w的取值范围cr≤w≤cc.

4 高铁快递主导下双方合作的Stackelberg博弈模型

采用逆向归纳法，先分别讨论在加性和乘性需求下，传统快递的最优决策模型.

4.1 传统快递最优决策模型

4.1.1 加性需求下的最优决策模型

基于文献[10]中库存因素的概念，引入协议运量因素z，根据加性需求函数的形式，设z=q-a+bp，其经济学意义为：当z＞ε时，协议运量超过市场需求，预订过剩；当z＜ε时，协议运量小于市场需求，预订不足.通过z可以清晰表示协议运量与市场需求之间的关系.将加性随机需求函数和z，代入式(1)，得到传统快递的利润函数表达式.

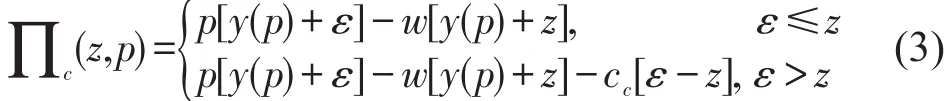
将利润的期望值表示为

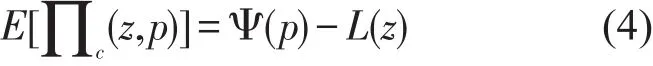
式中

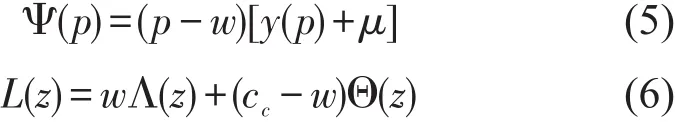
式(5)代表确定需求下的传统快递利润函数.式(6)代表需求随机变化所造成的利润损失函数.分别求对p的一阶、二阶偏导，可得

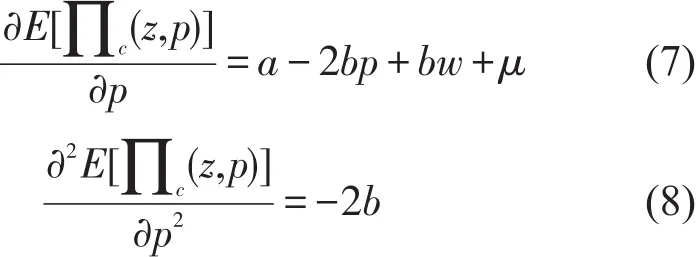
定理1高铁快递主导下，当随机需求为加性时，传统快递的最优市场定价p*是确定的，可表示为

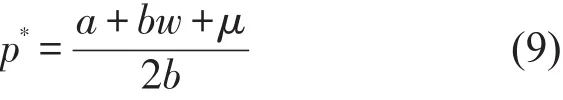
根据式(7)和式(8)可得定理1，将p*代入式(4)，可得最优协议运量的定理2.

定理2高铁快递主导下，当随机需求为加性时，传统快递的最优协议运量为q*=y(p*)+z*，对于取得最大值，q*可进一步表示为F(∙)的函数

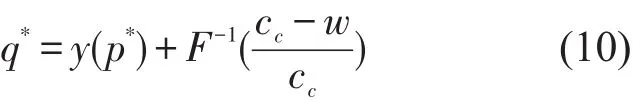
4.1.2 乘性随机需求函数下的最优决策模型

根据乘性随机需求函数的形式，将协议运量因素定义为z=q/y(p)，其经济学意义与加性需求中相同.将乘性随机需求函数和z代入式(1)，得到传统快递的利润函数表达式.

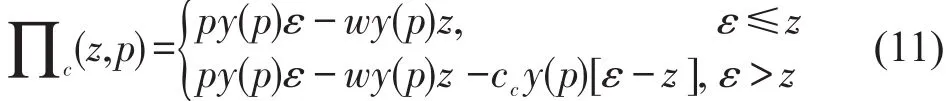
将传统快递的利润函数表示为

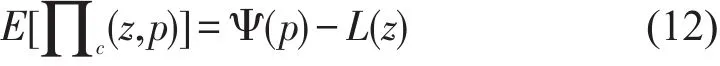
式中

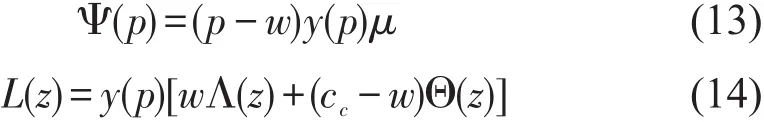
接下来，求解使利润期望函数E[∏c(z,p)]最大的p*、z*值，得到定理3和定理4.

定理3高铁快递主导下，当随机需求为乘性时，传统快递的最优市场定价p*是确定的，可由z（z=q/y(p)）的函数进行表示.

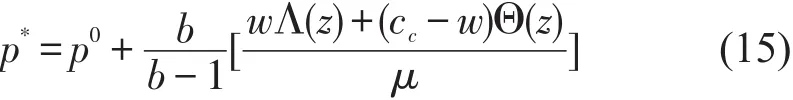
式中p0为需求确定情况下传统快递的最优市场定价且

定理4高铁快递主导下，当随机需求为乘性时，传统快递的最优协议运量为q*=y(p*)z*，在cc＞w时，对于A≤z≤B，存在唯一的,z*∈[A,B])使得E[∏c(z,p)]取得最大值，q*进一步表示为F(∙)的函数.

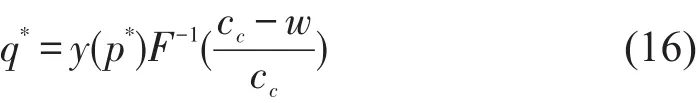
4.2 高铁快递最优决策模型

高铁快递预知到传统快递在加性、乘性随机需求下分别根据定理1～定理4确定市场运价和协议运量，因此，高铁快递在第一阶段的问题是

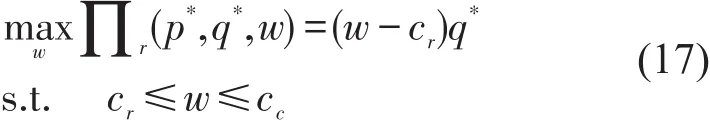
在加性需求下，根据定理1将p*,q*代入式(17)可得

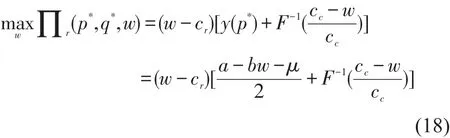
在乘性需求下，根据定理2将p*,q*代入式(17)可得

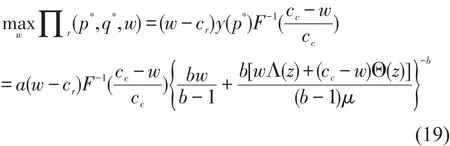
优化式（18）和式（19），可分别得到加性及乘性需求下高铁快递的最优协议定价策略，进而求得均衡解(p*,q*,w*).

5 传统快递主导下双方合作的Stackelberg博弈模型

传统快递主导下，传统快递优先对市场运价进行决策，高铁快递再对协议运价进行决策.最后，传统快递确定协议运量.采用逆向归纳法，先求得最后阶段传统快递的最优协议运量.

基于加性需求下传统快递利润函数（式（4））易得最优协议运量为

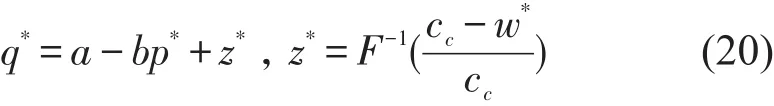
同理，乘性需求下最优协议运量为

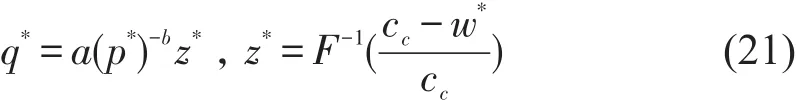
5.1 高铁快递最优决策模型

5.1.1 加性需求下的最优决策模型

高铁快递预知道传统快递根据式(20)确定协议运量，其在此阶段的问题为，由式(20)代入式(2)，可得

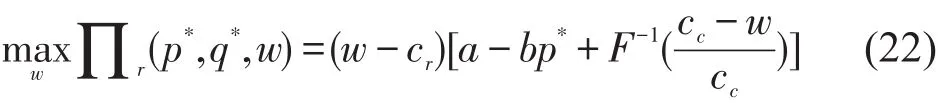
求解上式，可得高铁快递最优协议运价.

定理5传统快递主导下，当随机需求为加性时，高铁快递的最优协议运价为可由z的函数进行表示.

z满足条件

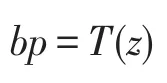
5.1.2 乘性需求下的最优决策模型

乘性需求下，传统快递根据式(21)确定协议运量，可得高铁快递最优协议运价.

定理6传统快递主导下，当随机需求为乘性时，高铁快递的最优协议运价为可由z的函数进行表示.

5.2 传统快递最优决策模型

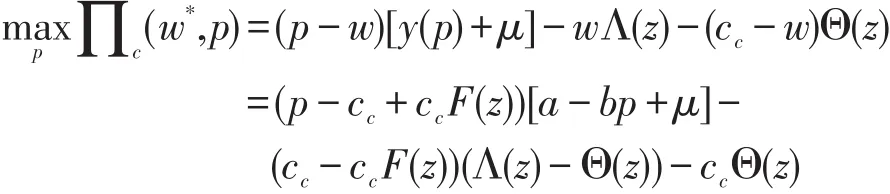
在乘性随机需求下，传统快递利润函数为式(12)，将式(24)代入式(12)可得

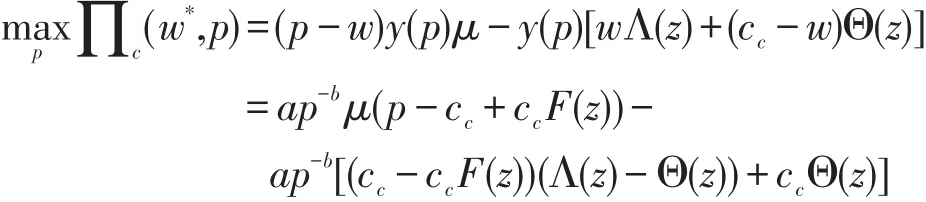
求解上述两式，可分别得到加性及乘性需求下传统快递的最优市场定价策略，进而求得均衡解(p*,q*,w*).

6 算例分析

假设加性和乘性需求中参数a、b及σ相同：a=100,b=3，σ=1/3，且加性、乘性需求中ε分别为[-1,+1]、[0,2]之间的均匀分布；高铁快递、传统快递的运输成本分别为cr=1、cc=4.分别基于加性和乘性随机需求函数计算供应链集中控制、高铁快递主导、传统快递主导、以及双方不合作时双方的最优决策及利润.表2、表3分别给出了计算结果.

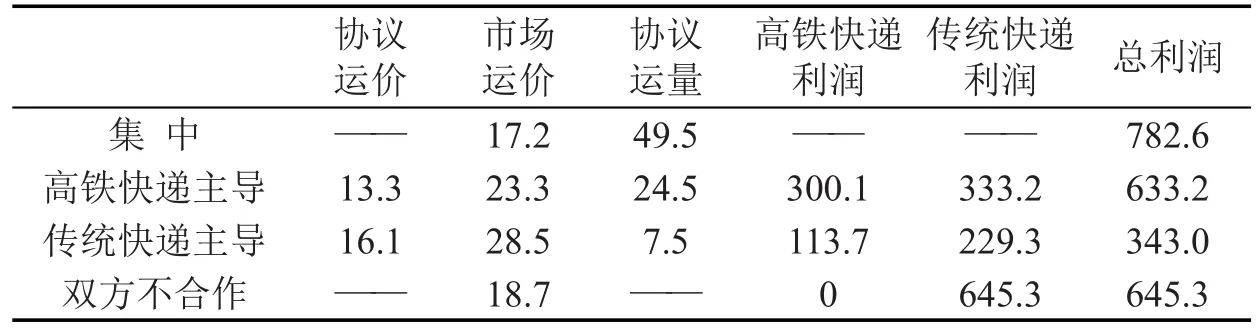
表2 四种情况下双方最优策略及利润（基于加性随机函数）Table 2The optimal strategy and profit in four cases（based on additive uncertain demand）

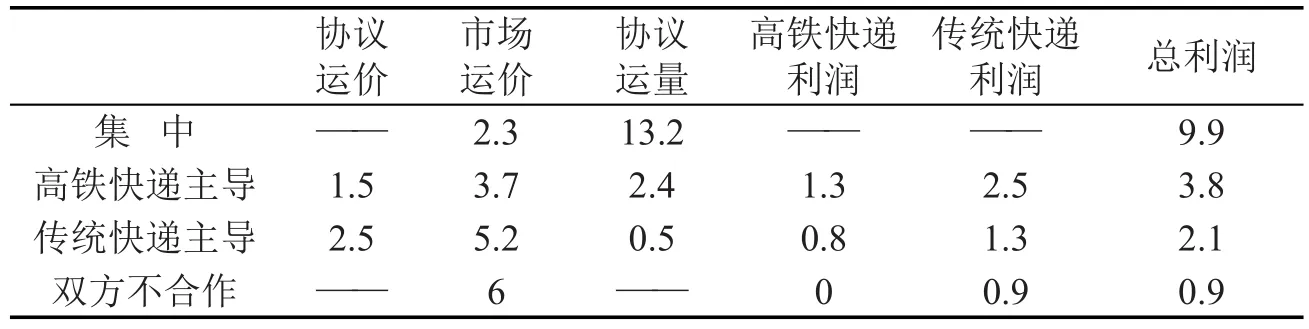
表3 四种情况下双方最优策略及利润（基于乘性随机函数）Table 3The optimal strategy and profit in four cases(based on multiplicative uncertain demand)

6.1 决策方式和主导权影响分析

根据表2、表3中相关数据可得：

(1)决策权的分散导致总利润（供应链效率）降低.

(2)高铁快递掌握主导时自身所获利润和供应链效率都大于传统快递主导时，而协议运价却低于传统快递主导时，即高铁快递掌握主导权对自身、供应链整体和快递客户都有利.

（3）加性需求中，传统快递不合作时的利润大于其合作时的利润，而在乘性需求中则相反，即当市场需求相对稳定时，传统快递选择不合作更有利；而当快递市场需求类似新产品市场需求，需求波动较大时，传统快递通过合作降低市场运价，提高市场需求规模，使双方都获益.

（4）在四种情况中，传统快递的利润都大于高铁快递的利润，这是由于本文模型不考虑库存成本和惩罚成本，且假设传统快递具有独立完成快递任务的能力.

6.2 市场需求波动影响分析

通过随机市场需求函数的方差反映市场需求的波动，加性、乘性随机市场需求函数的方差分别为

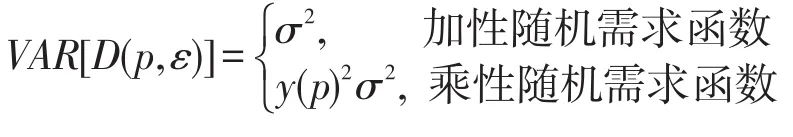
算例中，乘性随机函数中需求波动更大，高铁快递主导下在两种随机需求函数下双方的最优决策和利润对比图如图2所示.

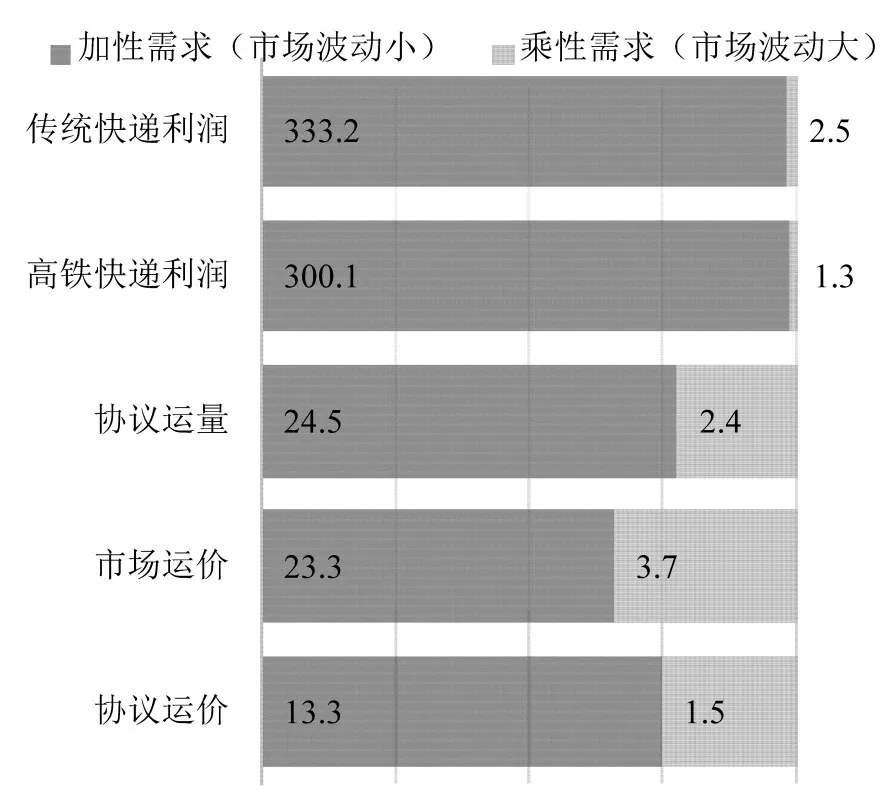
图2 不同需求函数下双方最优决策及利润Fig.2The optimal strategy and profits under different demand functions

可见，加性需求中双方利润远大于乘性需求中双方利润.即市场波动增大导致双方利润大幅减少.

7 研究结论

本文基于两种随机市场需求函数分别构建了高铁快递和传统快递主导下的Stackelberg博弈模型，得到结论：

(1)决策权的分散导致总利润降低.

(2)高铁快递掌握主导权可以增加自身利润和供应链效率，且对快递客户也有利.

(3)传统快递在合作中所获利润大于高铁快递所获利润；且在需求相对稳定时，传统快递不合作的利润更大；在需求波动与价格相关时，传统快递可通过合作降低市场运价获得更大利润.

(4)市场需求波动增大导致双方利润大幅减少.

因此，从快递行业可持续发展的角度，应通过兼并重组或形成物流企业联盟等方式使双方形成利益共同体，实现供应链集中控制，另外，高铁快递也应积极扩展客户资源，争取在合作中赢得主导权；对于传统快递，虽然在需求相对稳定时，选择不合作暂时更为有利，但为了避免市场需求波动带来的损失，解决自身结构性运力不足的问题，还是应该加强与高铁快递的合作.

[1]罗为东.关于高速铁路快件运输的探讨[J].铁道运输与经济,2013,35(10):56-59.[LUO W D.Discussion on high-speed railway express parcel transportation[J]. Railway Transport And Economy,2013,35(10):56-59.]

[2]魏晓洁.高铁快递:我国铁路多元化经营的战略创新[J].综合运输,2012,(7):51-55.[WEI X J.Highspeed railway express:China′srailway diversified businessstrategyinnovation[J].Comprehensive Transportation,2012,(7):51-55.]

[3]Gerchak Y,Wang Y.Revenue-sharing vs.wholesalepricecontracts in assembly systems with random demand[J].Production and Operations Management, 2004,13(1):23–33.

[4]Dong L,Rudi N.Who benefits from transshipment? Exogenousvs.endogenouswholesaleprices[J]. Management Science,2004,50(5):645-657.

[5]GeylaniT,DukesAJKSrinivasan.Strategic manufacturer response to a dominant retailer[J].Market Science,2007,26(2):164-178.

[6]雷丽彩,周晶.风险规避下的航空货运期权定价Stackelberg博弈模型[J].系统工程理论与实践,2010, 30(2):265-271.[LEI L C,ZHOU J.Stackelberg game model of capacity options for air cargo under risk aversion[J].Systems Engineering-Theory&Practice, 2010,30(2):265-271.]

[7]周蔷,刘长有.基于博弈理论的航空机票动态定价模型[J].江苏大学学报（自然科学版）,2013,34(4):481-485.[ZHOU Q,LIU C Y.Dynamic airline pricing model based on game theory[J].Journal of Jiangsu University(Natural science Edition),2013,34(4):481-485.]

[8]Petruzzi N C,DADA M.Pricing and the newsvendor problem:areviewwithextensions[J].Operations Research,1999,47(2):183-194.

[9]冯芬玲,李菲菲.基于期权理论的铁路货运定价模型[J].铁道科学与工程学报,2012,9(2):72-78. [FENG F L,LI F F.Pricing model of railway cargo transport based on option theory[J].Journal of Railway Science and Engineering,2012,9(2):72-78.]

[10]Jiang L,Wang Y.Supplier competition in decentralized assembly systems with price-sensitive and uncertain demand[J].Manufacturing&ServiceOperations Management,2010,12(1):93-101.

[11]Shi Zhang Ru.Impacts of power structure on supply chains[J].ProductionandOperationsManagement, 2013,22(5):1232-1249.

[12]Agrawal V,Seshadri S.Impact of uncertainty and risk aversion on price and order quantity in the newsvendor problem[J].Manufacturing&ServiceOperations Management,2000,2(4):410-423.

Price Strategy for CRH Express and Traditional Express Based on Stackelberg Game Model

DUAN Hua-wei1,2,YAN Yu-song1
(1.School of Transportation and Logistics,Southwest Jiaotong University,Chengdu 610031,China;2.Tianfu College, Southwestern University of Finance and Economics,Chengdu 610081,China)

In order to gain the optimal price strategy for CRH express and traditional express,and analyze the impact of dominance and uncertain demand on the price strategy,the Stackelberg game models between CRH express and traditional express considering different dominance under different uncertain demand are established.The optimal strategies for CRH express and traditional express in different cases are obtained by solving the models.The results reveal that:decentralized decision-making lead to a drop in profits;CRH express can get greater profits when it has the dominance;the traditional express always gets more profits than traditional express from cooperation;the increasing of randomness of market demand results in lower profits.

transportation economy;price strategy;Stackelberg game model;CRH express;traditional express uncertain demand

1009-6744（2015）05-0010-06

U-9

A

2015-04-09

2015-06-23录用日期：2015-07-01

四川省教育厅科研项目(14ZB0451).

段华薇(1983-)，女，讲师，博士生. ＊

8625776@qq.com