Existence and Numerical Solution for a Coupled System of Multi-term Fractional Differential Equations
2015-08-07YANGLifan杨李凡YEHaiping叶海平
YANG Li-fan(杨李凡),YE Hai-ping(叶海平)
College of Science,Donghua University,Shanghai201620,China
SOM IA Yassin Hussain Abdalkarim(苏美儿)1,2,ZHAO Li(赵俐)1,2*
1 College of Textiles,Donghua University,Shanghai201620,China
2 Key Laboratory of Textile Science&Technology,Ministry of Education,Donghua University,Shanghai201620,China
Existence and Numerical Solution for a Coupled System of Multi-term Fractional Differential Equations
YANG Li-fan(杨李凡),YE Hai-ping(叶海平)*
College of Science,Donghua University,Shanghai201620,China
An initial value problem was considered for a coupled differential system with multi-term Caputo type fractional derivatives.By means of nonlinear alternative of Leray-Schauder and Banach contraction principle,the existence and uniqueness of solutions for the system were derived.Using a fractional predictorcorrector method,a numerical method was presented for the specified system.An exam p le was given to illustrate the obtained results.
multi-term fractional differential equation;Caputo derivative;existence;uniqueness;numerical solution
Introduction
Fractional differential equations have been w idely used in various fields of science and engineering(see Refs.[1-3]). Among them,nonlinear coupled systems play an important role in heat transfer,electrode/electrolyte behavior,and subthreshold nerve propagation.Some attention has been paid to the coupled systems of fractional differential equations.Baiand Fang[4]established the existence of a positive solution to a singular coupled system of nonlinear fractional differential equations.Bashir and Ahmed[5]considered an initial value problem(IVP)for a coupled differential system of fractional order given by

and obtained some existence and uniqueness results by means of the nonlinear alternative of Leray-Schauder and Banach fixed point theorem.Besides,Su[6]concerned a two-point boundary value problem for a coupled differential system of fractional order and Ahmad and Nieto[7]studied three-point boundary problems at resonance.Some existence resultswere obtained.
In these investigations,existence results for a coupled neutral fractional system have been researched[8].Recently,Sun etal.[9]discussed a coupled system ofmulti-term nonlinear fractional differential equations given by
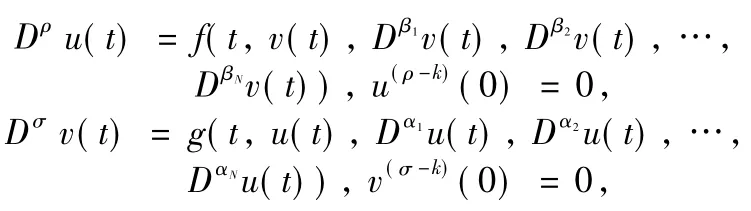
where t∈(0,1],0<αi,βi<1.By using Schauder fixed point theorem,they established the sufficient condition of existence for the system.Note that the fractional derivatives in Ref.[9]were the standard Riemann-Liouville derivatives.
As Pandey et al.[10]pointed out,Caputo definition can avoid(1)mass balance error,(2)hyper-singular improper integral,(3)non-zero derivative of constant,and(4) fractional derivative involved in the initial condition which is often ill-defined.In contrast to the Riemann-Liouville fractional derivative,the Caputo fractional derivative was shown to possess a suitable generalization of the extremum principle[11]. Therefore,in this paper,a coupled differential system with multi-term Caputo fractional derivatives is given by
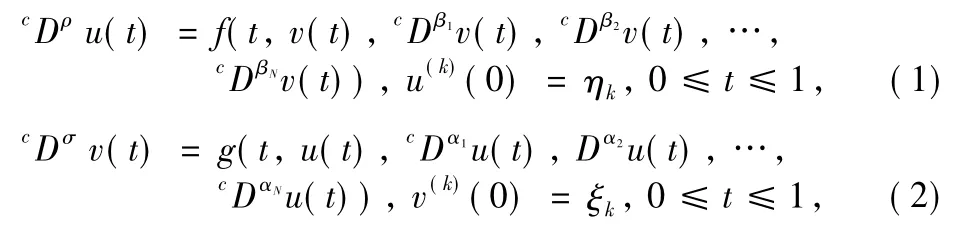
where f,g:[0,1]××…×→are given functions,cD denotes the Caputo fractional derivative,ρ,σ∈(m-1,m),αi,βi∈(ni-1,ni),m,ni∈,i=1,2,…,,ρ>β1>β2>…>βN,σ>α1>α2>…>αN,k=0,1,…,m-1,ρ,σ,αi,βi∉andηk,ξkare suitable real constants.By means of nonlinear alternative of Leray-Schauder theorem and Banach contraction principle,we derive the existence and uniqueness of solutions for the system.Also,a numerical method for the specified system is presented.An example is given and the results are compared with the exact solution.
The rest of the paper is organized as follows.In section 1,we give some relevant definitions and lemmas.The existence and uniqueness results are derived in sections 2 and 3,respectively.In section 4,the numerical method is presented. An example is given in section 5 and some conclusions are drawn in section 6.
1 Prelim inaries
Definition 1For a function f∈Cn([0,1]),the Caputo derivative of fractional orderα∈(n-1,n]is defined as[2]
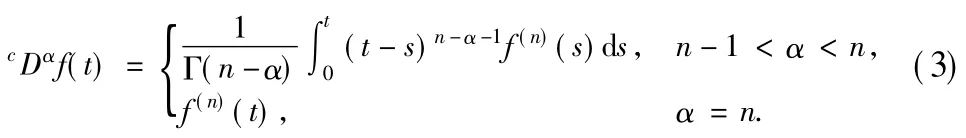
Definition 2[3]The Riemann-Liouville fractional integral of f of orderα>0 is given by

provided the right side is pointw ise defined on(0,+∞).
Lemma 1[12]Let f∈Cn([0,1]),n∈Ν,for anyα∈(n-1,n),then
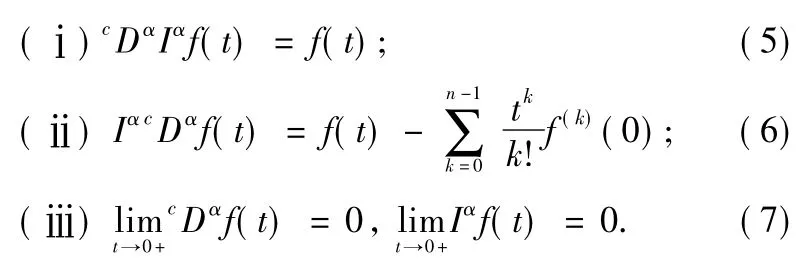
Remark 1It is worth pointing out that by this lemma,a differential equation(system)can be transformed to an integral one.
For power function,it follows as below.
Lemma 2[3]Letα∈(n-1,n),n∈Ν,andβ>n.Then the follow ing relations hold
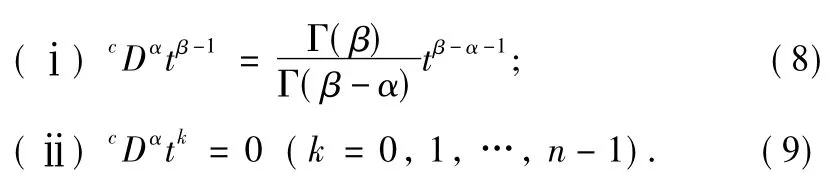
To establish existence and uniqueness criteria of solution for Eqs.(1)and(2),we introduce the follow ing notations and lemmas.

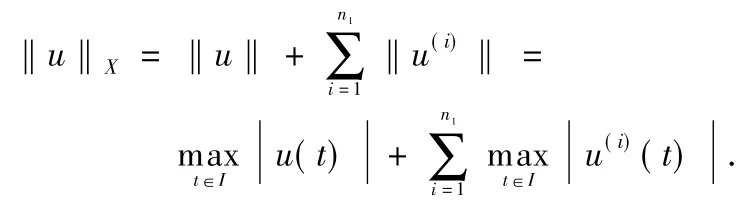
and S=X×X,endowed with the norm
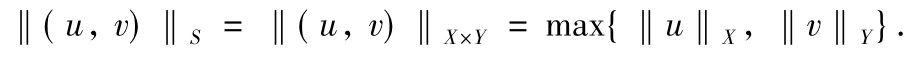
It can be easily proved that(S,‖·‖S)is a Banach space.
The rest part of this section will be devoted to establishing the equivalence between Eqs.(1)and(2)and the follow ing integral equations:
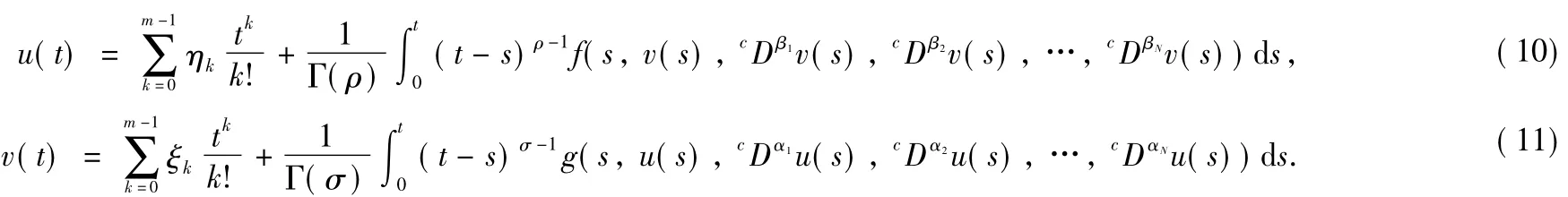
Lemma 3Let f,g:[0,1]××…×→be continuous functions defined on I.Then(u,v)∈S isa solution of Eqs.(1) and(2)if and only if it is the solution of Eqs.(10)and(11).
ProofBased on Eq.(6),one can easily find that if(u,v)∈S is a solution of Eqs.(1)and(2),then Eq.(1)can be transformed to Eq.(10)and Eq.(2)must be equivalent to Eq.(11).That is,(u,v)must be a solution of coupled integral system(Eqs.(10)and(11)).
Conversely,let(u,v)∈S be a solution of system Eqs. (10)and(11),then putcDρandcDσinto the both sides of Eqs.(10)and(11),respectively.Taking Eqs.(5),(7)and (9)into consideration,we obtain
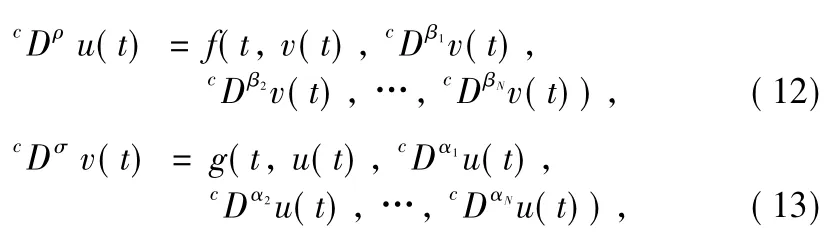
Furthermore,by Eq.(10),the i th order derivative of u(t) can be concluded as
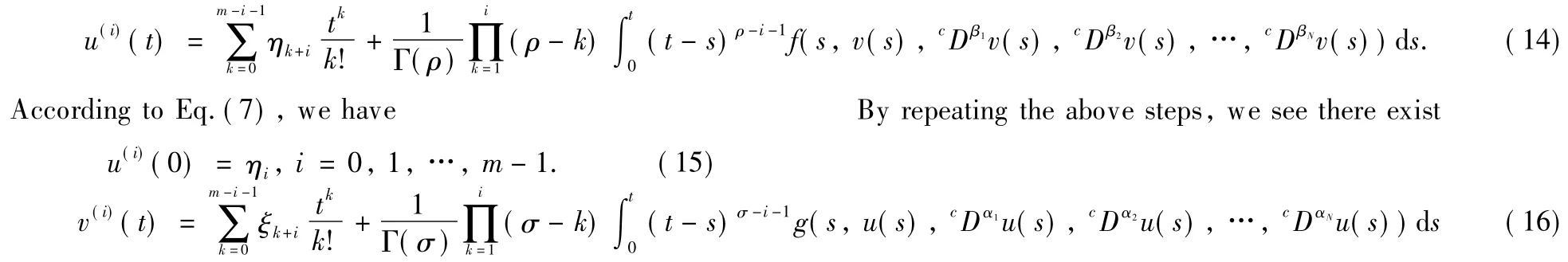
and

From Eqs.(12),(15)and Eqs.(13),(17),we figure out that if(u,v)∈S is a solution of system(Eqs.(10)and (11)),itmust be the solution of Eqs.(1)and(2).This completes the proof.
2 Existence Result
Firstly,we introduce the follow ing lemma called the nonlinear alternative of Leray-Schauder.
Lemma 4[13]Let X be a normed linear space,M⊂X be a convex set,and N be open in M with 0∈N.F:→M is a continuous and compact mapping.Then either the mapping F has a fixed point inor there exist l∈∂N andλ∈(0,1),which will lead to l=λFl.
For the sake of convenience,the follow ing notations are needed.Let the operator P:S→S be given by
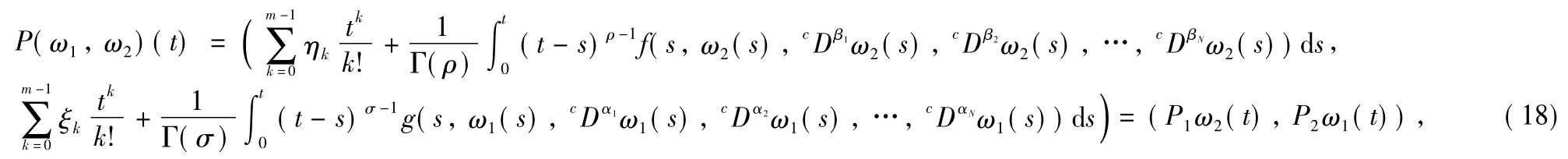
and

By now,all the preparations have been made,so we can show our existence result favorably.
Theorem 1Let f,g:[0,1]××…×→be continuous functions.And there exist nonnegative functions a(t),a0(t),a1(t),…,aN(t),b(t),b0(t),b1(t),…,bN(t)∈L(I)
such that
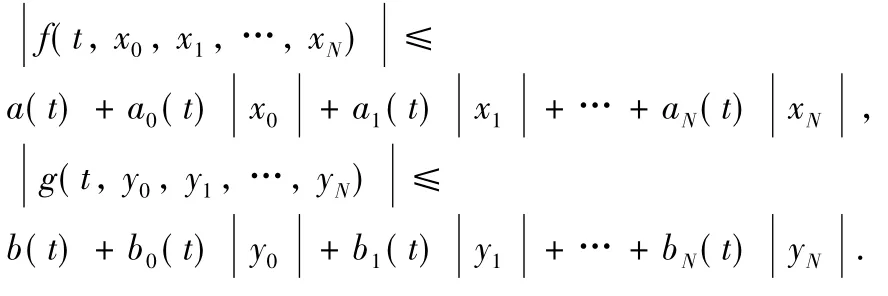
If 0<B<∞,0<C<1,then coupled system Eqs.(1)-(2)have a solution,where
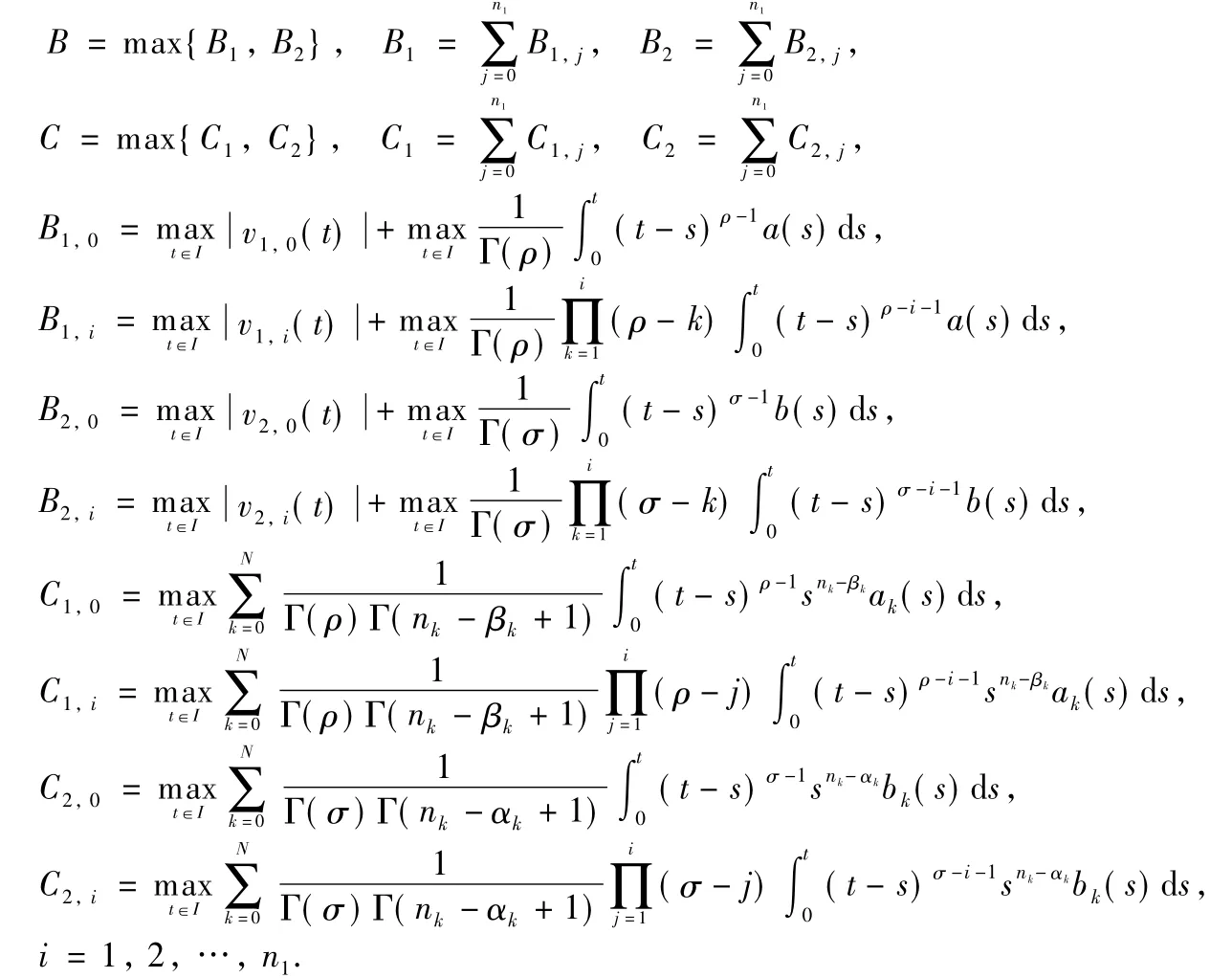
ProofObviously,the solution of Eqs.(1)and(2) coincideswith the fixed point of the operator P.Therefore,it's necessary to prove the existence of the fixed point by means ofLemma 4.Precisely,it comes out that there exists a fixed point of the operator in a“ball”U in the Banach space S.Define
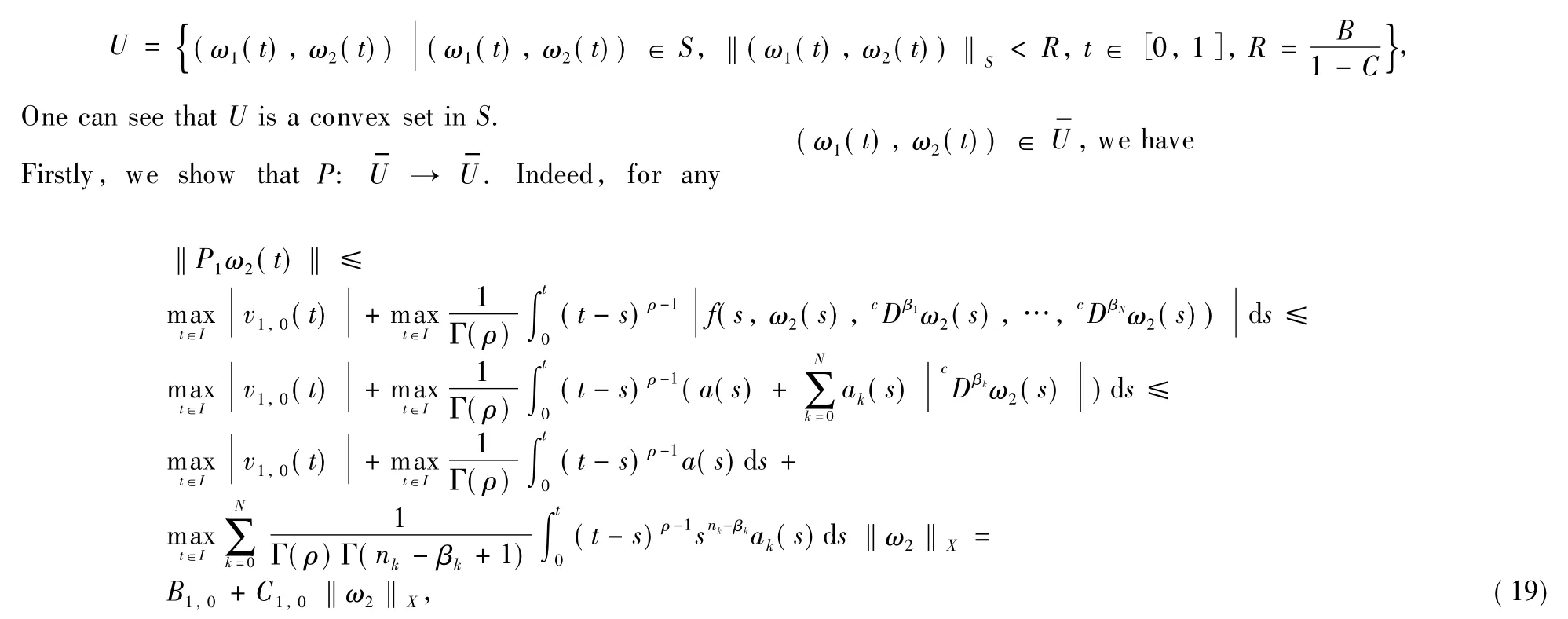
and similarly
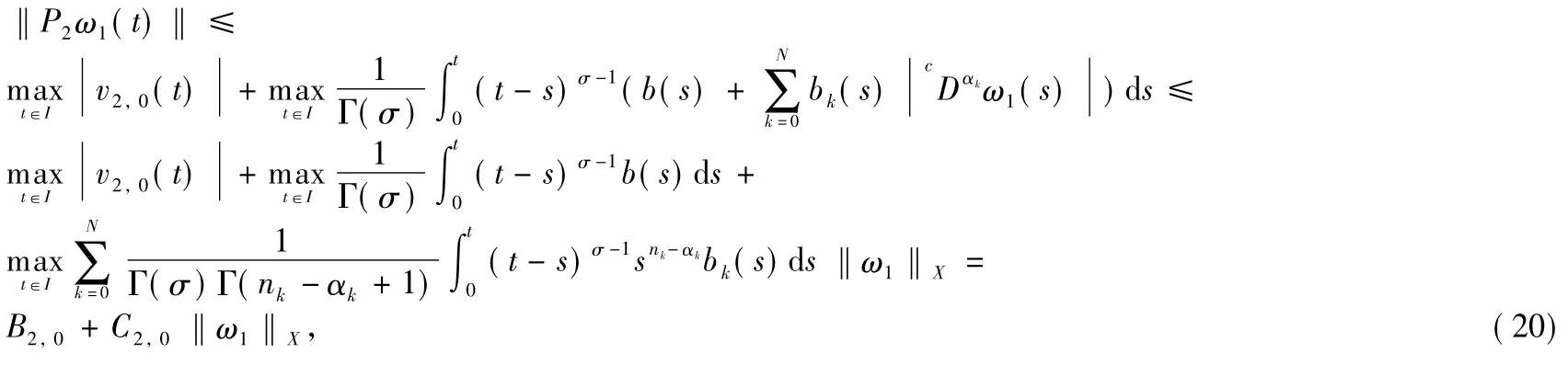
whereβ0=0,n0=0.From Eqs.(14)and(16),for any i=1,2,…,n1,we have

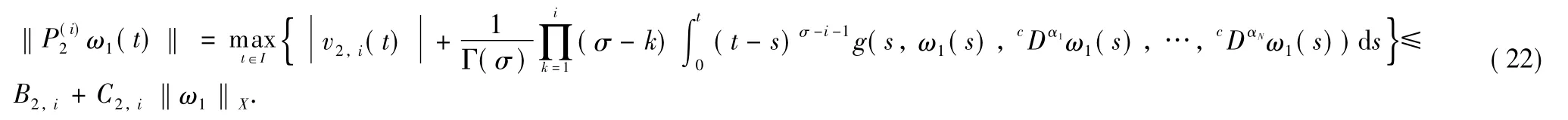
Now,note that
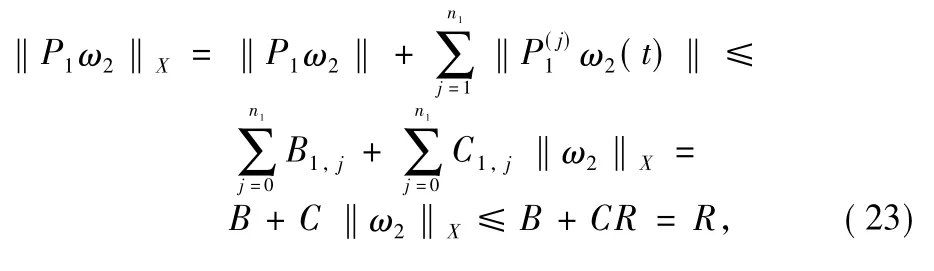
and
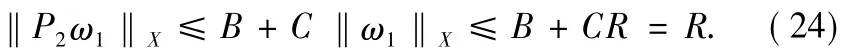
In the next part,we show that the operator P is continuous and compact.For convenience,denote
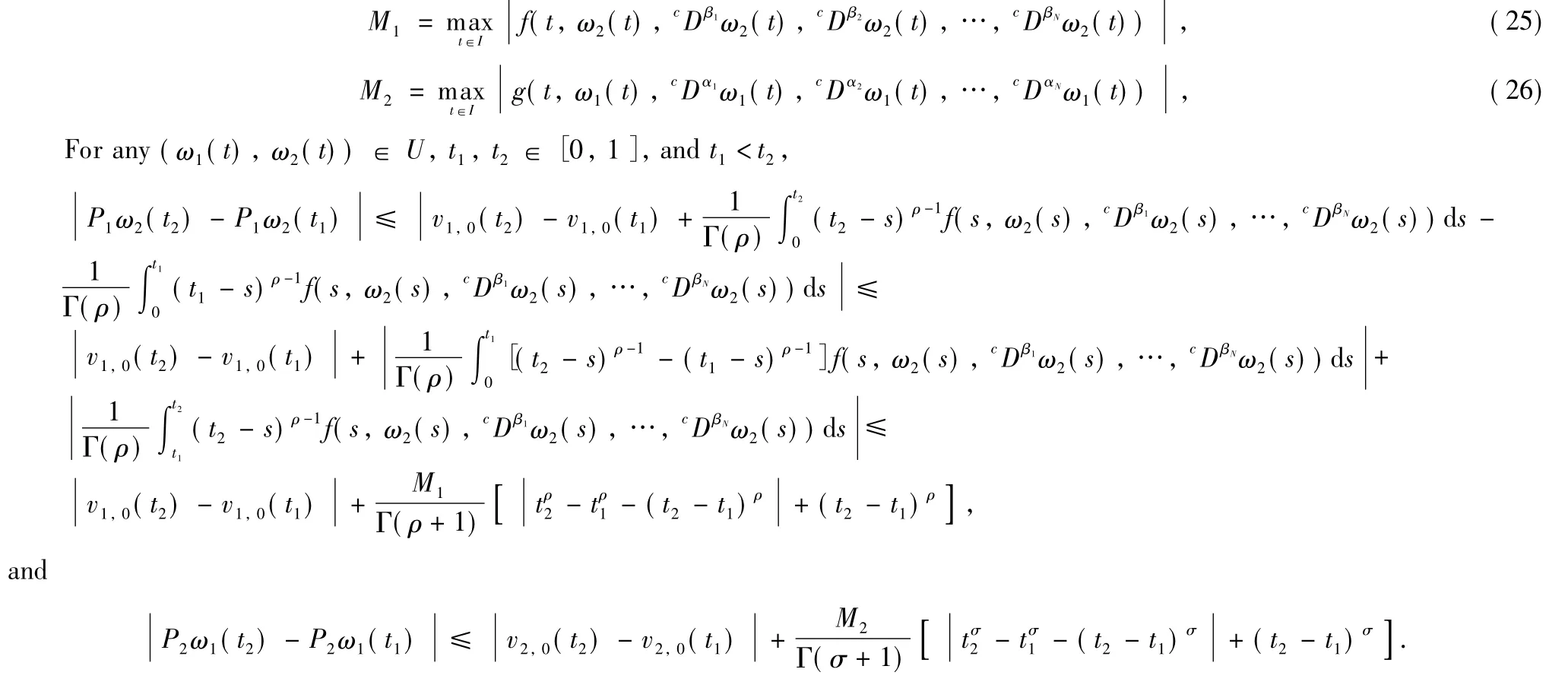
Due to the uniform ly continuous property of the power functions,one can figure out that PU is an equicontinuous set.Apparently,PU⊆.Therefore,the operator P is completely continuous.
In view ofLemma 4,it is necessary to consider the eigenvalue problem given by
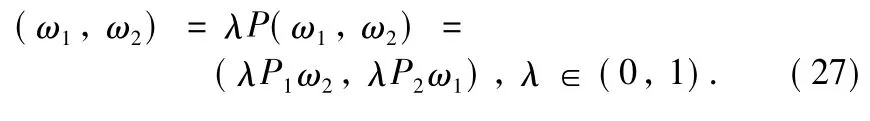
As a solution(ω1,ω2)of the above for 0<λ<1,we take Formulas(23)-(24)into consideration and find that
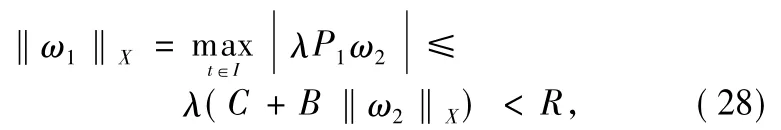
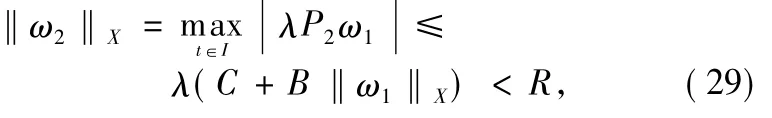
which implies that(ω(t),ω(t))∉∂U,By Lemma 4,P
12has a fixed point in
This completes the proof.
3 Uniqueness Result
In this section,we focus on establishing the sufficient conditions of the uniqueness of solution for the coupled system (Eqs.(1)and(2))by Lipschitz type assumptions as follows.
(H)Let f,g:[0,1]×R×…×R→R be continuous functions.And there exist nonnegative functionsδ1,0(t),δ1,1(t),…,δ1,N(t)andδ2,0(t),δ2,1(t),…,δ2,N(t)such that
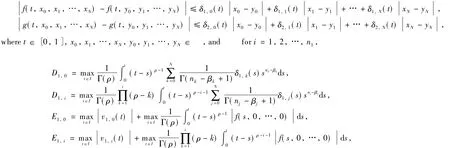
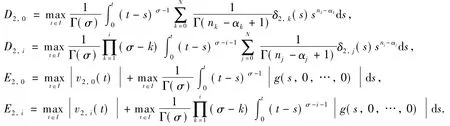
Theorem 2If the assumption(H)holds and 0<D<1,0<E<∞,then the system(Eqs.(1)and(2))has a unique solution,where
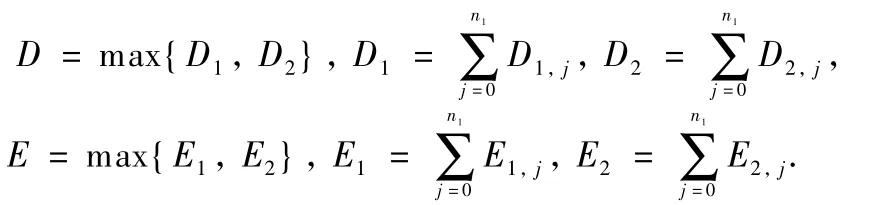
ProofAttention is focused on that the operator P given by Eq.(18)has a unique fixed point in,where U=

Furthermore
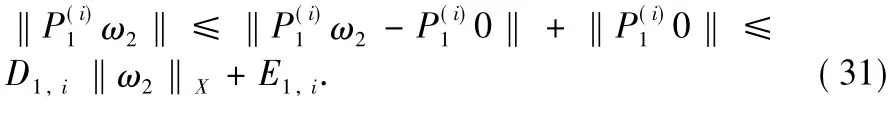
Similarly

It follows that
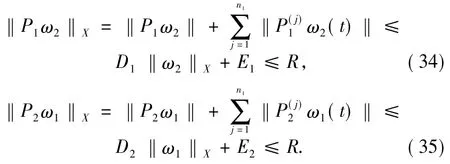
Therefore,it appears that P:→.
What's more,enlightened by the estimation above,we obtain


Hence,
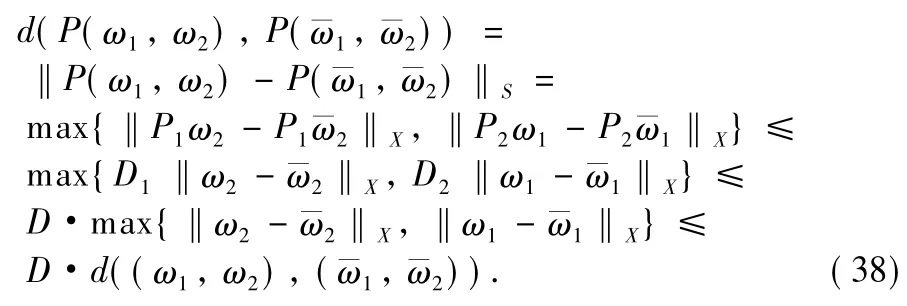
Since 0<D<1,by the Banach contraction principle,the operator P has a unique fixed point in U-.That is,there is a solution of the coupled integral Eqs.(10)and(11).
This completes the proof.
4 NumericalMethod
Due to themathematical complexity of analytical solutions for the fractional coupled system,it demands an effective and easy-to-use numerical scheme for solving such equations.It should be noticed that the numerical approximation of linear multi-term FODEswas investigated by Garrappa[14].Also,the predictor-correctormethod,as a stable and effective way,was promoted for fractional differential systems[15].It works whether it is for linear or nonlinear equations,and itmay be extended to multi-term FODEs.Using the fractional predictorcorrector method,we present a numerical method for the coupled system(Eqs.(1)and(2)).
Firstly,we rew rite the system(Eqs.(1)and(2))as[16]

with initial conditions
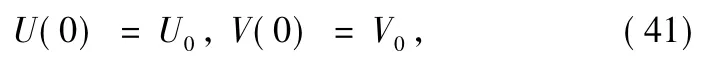
whereγ=1/M,M is the least common multiple of the denom inators ofρ,σ,α1,…,αN,β1,…,βN,
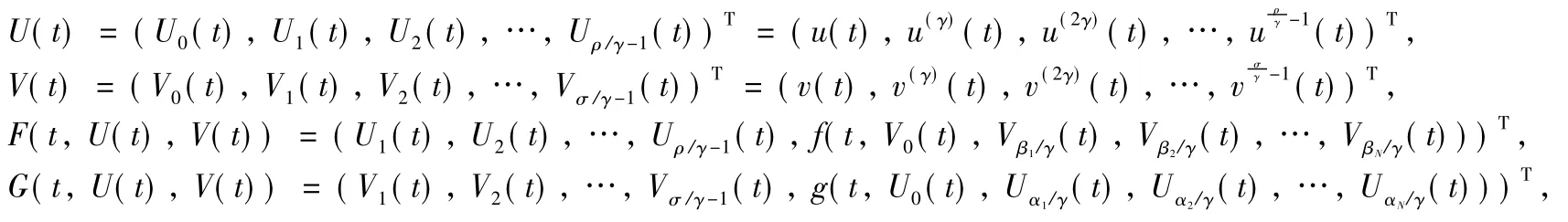
and
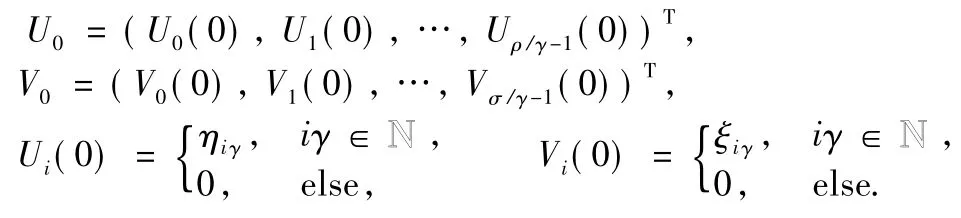
The system(39)-(40)is equivalent to the follow ing Volterra integral system

A obp tpa li yn in thg e p th ree dic f treadc ti voanl uale predictor-corrector method[15],we


where h is chosen as suitable iteration step,tj(j=0,1,…,n +1)are nodes in interval I,and
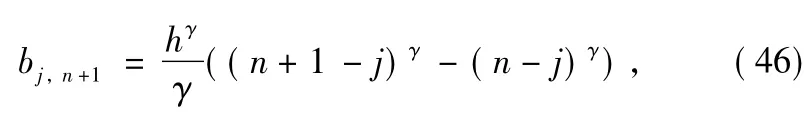
and corrector formula is given by
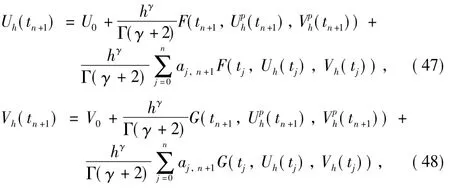
where

5 An Exam p le
Consider the follow ing fractional coupled system
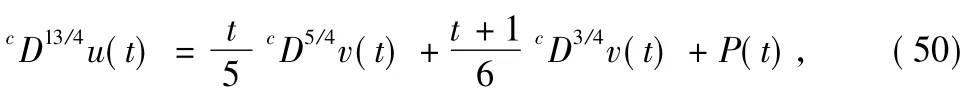
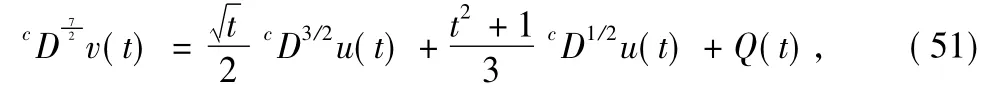
with initial condition
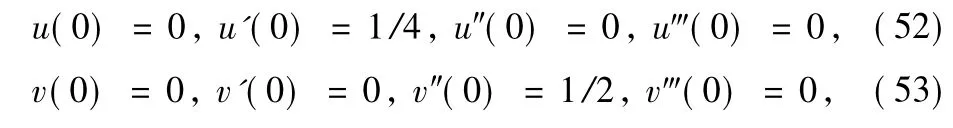
where

To prove the uniqueness of solutions for Eqs.(50)-(53) we need to verify the assumptions of Theorem 2.Here I=[0,1],ρ=13/4,σ=7/2,β1=5/4,β2=3/4,α1=3/2,α2= 1/2 andη0=0,η1=1/4,η2=0,η3=0,ξ0=0,ξ1=0,ξ2=1/2,ξ3=0.Withδ1,1(t)=t/5,δ1,2(t)=(t+1)/6,δ2,1(t)=■t/2,δ2,2(t)=(t2+1)/3,we obtain D1,0≈0.021,D1,1≈0.083,D1,2≈0.515,D1=D1,0+D1,1+D1,2≈0.619<1,D2,0≈0.026,D2,1≈0.114,D2,2≈0.389,D2=D2,0+D2,1+D2,2≈0.529<1,E1,0≈0.505<∞,E1,1≈1.280<∞,E1,2≈3.142<∞,E2,0≈0.505<∞,E2,1≈1.531<∞,E2,2≈3.664<∞.
In view of Theorem 2,the system(Eqs.(50)-(53))has a unique solution.Indeed,the explicit solution of the system is u(t)=(t+t4)/4,v(t)=(t2+t4)/4.
On the other hand,using the numericalmethod described in section 4,we obtain the numerical solution of the system Eqs.(50)-(53).
A comparison of the exact solution and the numerical solution is shown in Figs.1 and 2.It appears that the numerical solutions perform in good agreementwith the exact ones.
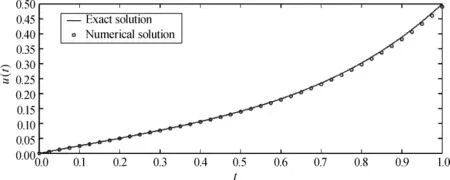
Fig.1 Exact solution(line)and numerical solution(symbol)of u(t)with h=0.005
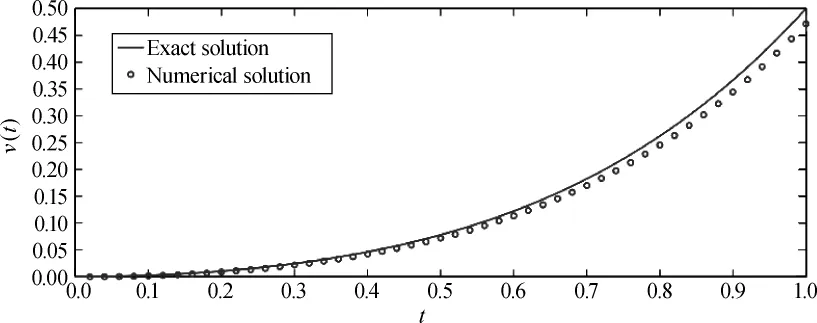
Fig.2 Exact solution(line)and numerical solution(symbol)of v(t)with h=0.01
6 Conclusions
This paper concerns about fractional coupled system involved with multi-term Caputo derivatives.By nonlinear alternative theorem and Banach contraction principle,the existence and uniqueness results are obtained.Furthermore,a numericalmethod for fractional coupled system is presented.An example is given to verify the effectiveness of the theorems and the numerical scheme.
[1]Samko SG,Kilbas A A,Marichev O I.Fractional Integrals and Derivatives:Theory and Applications[M].Yverdon:Gordon and Breach Science Publishers,1993.
[2]Podlubny I,Fractional Differential Equations[M].New York: Academ ic Press,1999.
[3]Kilbas A A,Srivastava H M,Trujillo J J.Theory and Applications of Fractional Differential Equations[M]. Netherlands:Elsevier Science Limited,2006.
[4]Bai C,Fang J.The Existence of a Positive Solution for a Singular Coupled System of Nonlinear Fractional Differential Equations[J].Applied Mathematics and Computation,2004,150(3): 611-621.
[5]Bashir A,Ahmed A.Existence and Uniqueness of Solutions for Coupled Systems of Higher-Order Nonlinear Fractional Differential Equations[J].Fixed Point Theory and Applications,2010,doi: 10.1155/2010/364560.
[6]Su X.Boundary Value Problem for a Coupled System of Nonlinear Fractional Differential Equations[J].Applied Mathematics Letters,2009,22(1):64-69.
[7]Ahmad B,Nieto J J.Existence Results for a Coupled System of Nonlinear Fractional Differential Equations with Three-Point Boundary Conditions[J].Computers and Mathematics with Applications,2009,58(9):1838-1843.
[8]Liu S Y,Wang G T,Zhang L H.Existence Results for a Coupled System of Nonlinear Neutral Fractional Differential Equations[J].Applied Mathematcs Letters,2013,26(12):1120-1124.
[9]Sun SR,LiQ P,LiY N.Existence and Uniquenessof Solutions for a Coupled System of Multi-term Nonlinear Fractional Differential Equations[J].Computers and Mathematics with Applications,2012,64(10):3310-3320.
[10]Pandey R K,Singh O P,Baranwal V K.An Analytic Algorithm for the Space Time Fractional Advection Dispersion Equation[J]. Computer Physics Communications,2011,182(5):1134-1144.
[11]Luchko Y.Maximum Principle and its Application for the Time-Fractional Diffusion Equations[J].Fractional Calculus and Applied Analysis,2011,14(1):110-124.
[12]Li C,Deng W.Remarks on Fractional Derivatives[J].Applied Mathematics and Computation,2007,187(2):777-784.
[13]Fucik S,Kufner A.Nonlinear Differential Equations[M].New York:Elsevier Science Ltd.,1980.
[14]Garrappa R.Stability-Preserving High-Order Methods for Multiterm Fractional Differential Equations[J].International Journal of Bifurcation and Chaos,2012,22(4),doi:1142/ S0218127412500733.
[15]Diethelm K,Ford N J,Freed A D.A Predictor-Corrector Approach For the Numerical Solution of Fractional Differential Equations[J].Nonlinear Dynamics,2002,29(1/2/3/4):3-22.
[16]Diethelm K.The Analysis of Fractional Differential Equations:an Application-Oriented Exposition Using Differential Operators of Caputo Type[M].Heidelberg:Springer,2004.
Finishing Effect on Warm th Property of Cotton/Kapok Blended Knitted Fabric
SOM IA Yassin Hussain Abdalkarim(苏美儿)1,2,ZHAO Li(赵俐)1,2*
1 College of Textiles,Donghua University,Shanghai201620,China
2 Key Laboratory of Textile Science&Technology,Ministry of Education,Donghua University,Shanghai201620,China
Abstract:Nowadays,more and more naturalor functional fibers are being investigated due to their utilization in thermal underwear.Kapok fiber is one of the natural cellulosic fiberswhose source is the kapok p lant.It has hollow body and sealed tail,which exhibits desirable features required for functional textiles of this nature.In this study,cotton/kapok(80/20 by mass)blended yarn with two types of yarn size 18.5 and 14.8 tex,respectively are knitted into plain stitches.The fabrics are undergone with an optimal preparation p lan according to orthogonal design.Then,after dyeing and softening,fabric properties including thermal and water-vapour resistances,w icking property,pilling behaviour,and surface morphology,are tested and scrutinized for their candidacy for thermal underwear.The results showed that cotton/kapok blended fabrics have good thermal resistance which is significantly higher than those of cotton/modal blended fabrics,and the same water vapour resistance compared with cotton/modal blended fabrics which are normally used as underwear.Cotton/modal blended knitted fabrics has better pilling grade than cotton/kapok blended fabrics.M eanwhile,the cotton/kapok blends fabrics have good w icking property.Collectively,it was concluded that cotton/kapok blended fabric was appropriate for thermal underwear.However,themain lim itation of these fabrics is their pilling properties.
Keywords:cotton/kapok blended yarn;knitted fabric;orthogonal design;performance;thermal underwear
CLCnumber:TS941.6Documentcode:AArticleID:1672-5220(2015)04-0620-06
Introduction
Underwear,is one of the most important garments for human clothing for all seasons,because it supports the human skin adaptable to the body heat balance such as warm th or cold[1].Today,themajor function of the garments is to build regulation system for keeping body temperature at the mean value even though physical activities and outer atmospheric conditions change spatially underwear[2-3].Underwear has become the second type of garment manufacturing sector in whole world.To date,many textilematerials have been used to produce underwear.Firstly,synthetic fiber such as polyester and nylon has been used as underwearmaterials but these types ofmaterials are uncom fortable clammy,clingy and sweaty[4]. For all these reasons,some researchers declare the use of natural fibers,especially those which contain 100%cotton,or cottonblends,because it can bemore com fortable for human body to absorb water vapors and perspiration than synthetic fibers[5-7]. Therefore,com fort,which is defined as an agreeable state of physical and psychological conformity between environmentand human being becomes the main feature along with the development of textile technology[8-9].Thus,human body in contact with garment fabric is associated with three main factors:sensorial,thermal and physiological.Thermophysiological com fort is a general expression for factors such as sweat absorption,water vapor transmission,drying ability and thermal properties of fabrics[10-11].Underwear manufacturers used different types of structures of fabrics such as woven and knitting.The structure of knitted fabrics has significant parameter estimated for influencing the moisture and thermal management properties of garment than woven structure[11]. The most important factors influencing heat transfers through fabrics are enclosed air and thickness.Reduction in thickness of fabric,together with corresponding decrease of fabric volume,is normally followed by the decrease of air entrapped in fabric structure changing the overall thermal properties of the fabric[12-13].However,more studies have been focused on kapok fibers characterization,structure,batting and spinning. Thus,kapok fibers are usually blended with other fibers to spin yarn instead of spinning into pure kapok yarn due to their defects such as short length,smooth surface and low strength[14].From previous studies,few researches focused on com fort properties of cotton/kapok fabric underwear.
Themain intention of this study is to find the advantages and disadvantages of cotton/kapok blended knitted fabrics through the whole process of manufacturing.Moreover,the thermal and water-vapor resistances,w icking property,pilling behavior,and surfacemorphology have been evaluated in order to determine the utilization of cotton/kapok blended yarn for knitted fabrics used in thermal underwear,and meanwhile to give some advice for the spinning factory in order to improve their spinning techniques and produce qualified cotton/kapok blended yarns.
1 Materials and Methods
1.1 M aterials and knitted fabrics
Kapok fiber is one kind of natural cellulose fiber and the cross section area of the kapok fiber is oval to round shown in Fig.1[15].IR spectra clearly indicated thatkapok fiber is similar to cotton fibers,but XRD showed that the degree of crystalline of kapok fiber is 46.4%,less than cotton fibers 70.3%.The strength and elongation of the kapok fiber is lower compared with cotton fibers,because it's lower crystalinity and thinner cell structure[16].
In this study two types of yarns(18.5 and 14.8 tex)were used and produced from cotton/kapok blended fibers.Themass ratio of blended fiberswas80%cotton and 20%kapok obtainedfrom Xiajin Fengrun Textile Co.,Ltd.,Shandong Province,China Cotton/kapok knitted fabricsweremanufactured on B.C. M circular knitting machine(Ban Yan Tai International Co.,Ltd.,Fujian Province,China)with 28 gauges and 16 diameters inch.

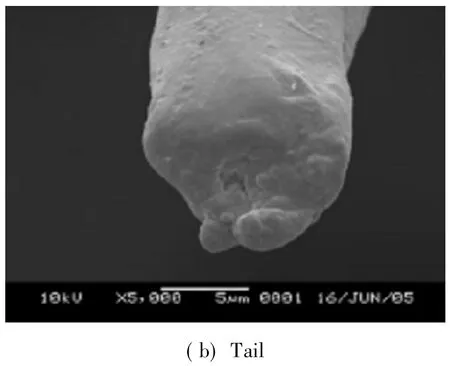
Fig.1 Kapok fiber
1.2 Scouring and bleaching
The scouring and bleaching agents,which affect properties of cotton/kapok blended fabrics,are studied.Because of the lower crystalinity,strength and elongation of kapok fiber compared with cotton fiber,the preparation of kapok fiber should be differentiated with cotton fiber.The method of orthogonal array L9(34)is used to determ ine the optimal method of treating the fabric to meet the demand of thermal underwear.This experiment has four variables at three different levels.Levels indicate that three types of concentrations have been used in the scouring process.Them inimum concentration is level1,the medium concentration is level 2,and level 3 is themaximum concentration of the chem ical agents.Some other experimental parameters,such as temperature,liquor ratio,and time are selected as 90℃,1∶50,and 2 h,respectively.A four factor and three level factorial design is used to evaluate the follow ing factors.Concentrations of NaOH(A),H2O2(B),Na2SiO3(C),and surface active agent(SAA)(D)are based on the weight of fabrics(o.w.f).The factors and their respected levels are shown in Table 1 and several experiments are preformed as shown in Table 2.
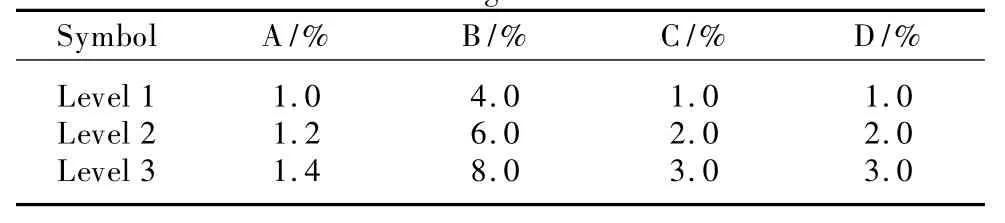
Table 1 Design of factor level
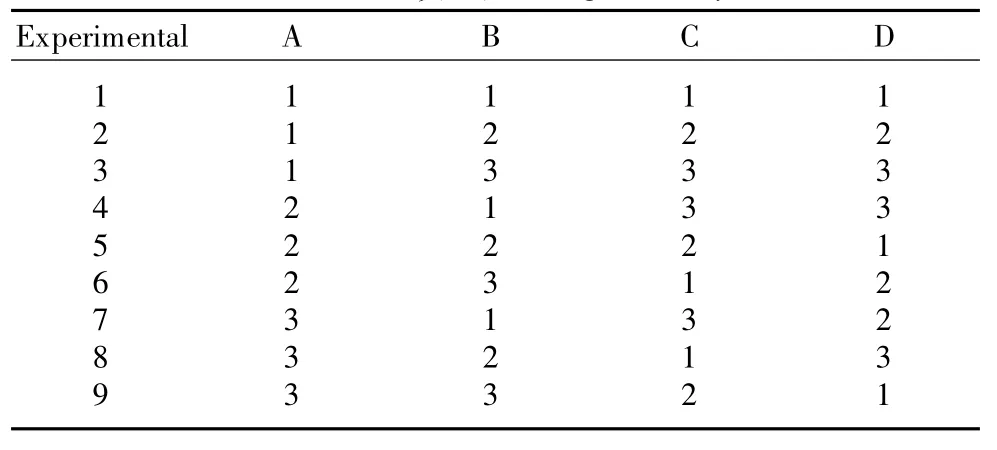
Table 2 L9(34)orthogonal array
1.3 Orthogonal array analysis
According to the assignment of the experiment,the mean of property for the corresponding factors at each level is calculated.The mean ratio values and the range of mean are calculated for each factor and each levelas shown in Table3.In Table 3,KA1,KA2 and KA3 are submission values of levels 1,2 and 3.And kA1,kA2 and kA3 aremean values for levels 1,2 and 3 respectively.The range R(the difference between the mean values of the highestand the lowest)for each parameter is also calculated.The larger the R value for a parameter,larger the effect of the variable has on the process.Based on the overall evaluation of the results,1.4%,8.0%,2.0%and 1.0%have been selected for concentrations of NaOH,H2O2,Na2SiO3and S.A.A,respectively as the optimum level.
1.4 Dyeing and finishing
Dying bath contains 0.5%-1.0%reactive dye(o.w.f),liquor ratio is 1∶50,NaCl is 15.0-30.0 g/L and Na2CO3is 10.0 g/L.After dyeing process,SoulsoftWALIQ(50.0 g/L) was used as the softener with liquor ratio 1∶50 at 40℃for 30 min.Figure 2 is the schematic presentation of dyeing and finishing.
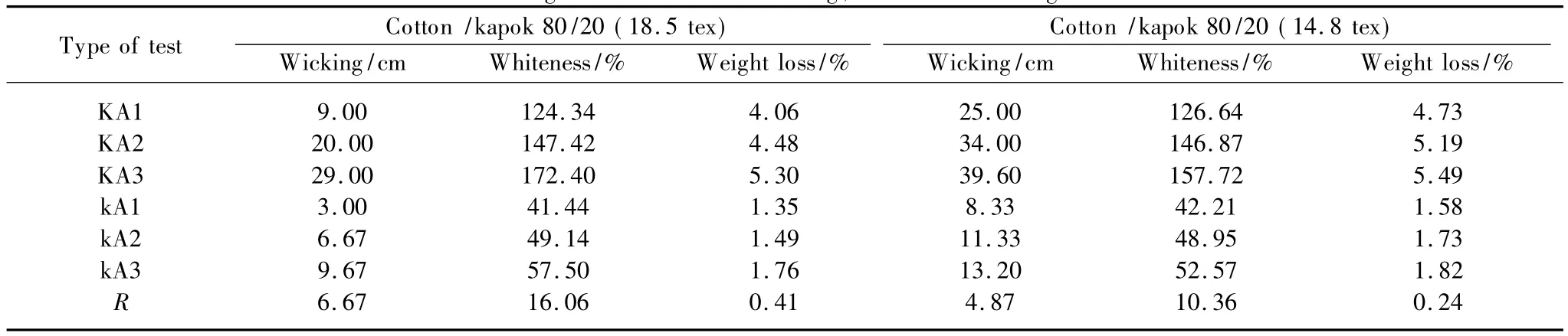
Table 3 Design of factor level of wicking,whiteness and weight loss tests

Fig.2 Schematic presentation of dyeing and finishing
2 Testing Methods
Thermal and water-vapor resistances under steady-state conditions are measured by YG606G ventilated thermal wet tester(Ningbo Textile Instrument Factory,China)according to GB/T11048—2008[17].A vertical w icking effect is measured according to AATCC TM 197—2011,and pilling of the fabrics is measured by YG401E fabric abrasion tester Martindale (Ningbo Textile Instrument Factory,China)according to ISO 12945—2:2000.The surface morphology of cotton/kapok blended fabric is observed by using a scanning electron microscope(SEM).
3 Results and Discussion
3.1 Thermal com fort properties
Figure 3 shows the relationship of fabric thickness and thermal resistance,(a)and(b)are cotton/kapok blended fabricswith yarn size 18.5 and 14.8 tex,respectively and(c) is cotton/modal blended fabric(50/50 by mass)with yarn size 14.8 tex.According to the results,it is observed that the thermal resistance of all fabrics types has linear correlation with thickness.As the fabric thickness decreases,the thermal resistance value also decreases.Consequently,with decrease in fabric thickness,the thermal resistancewill decrease as given in Eq.(1).

where R is the thermal resistance(m2·K·W-1),h is the thickness(mm),andλis the thermal conductivity(W·m2· K-1).
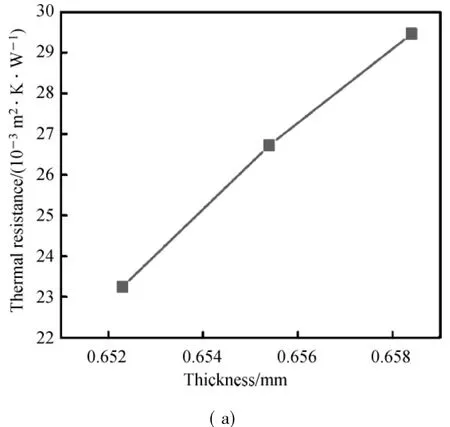
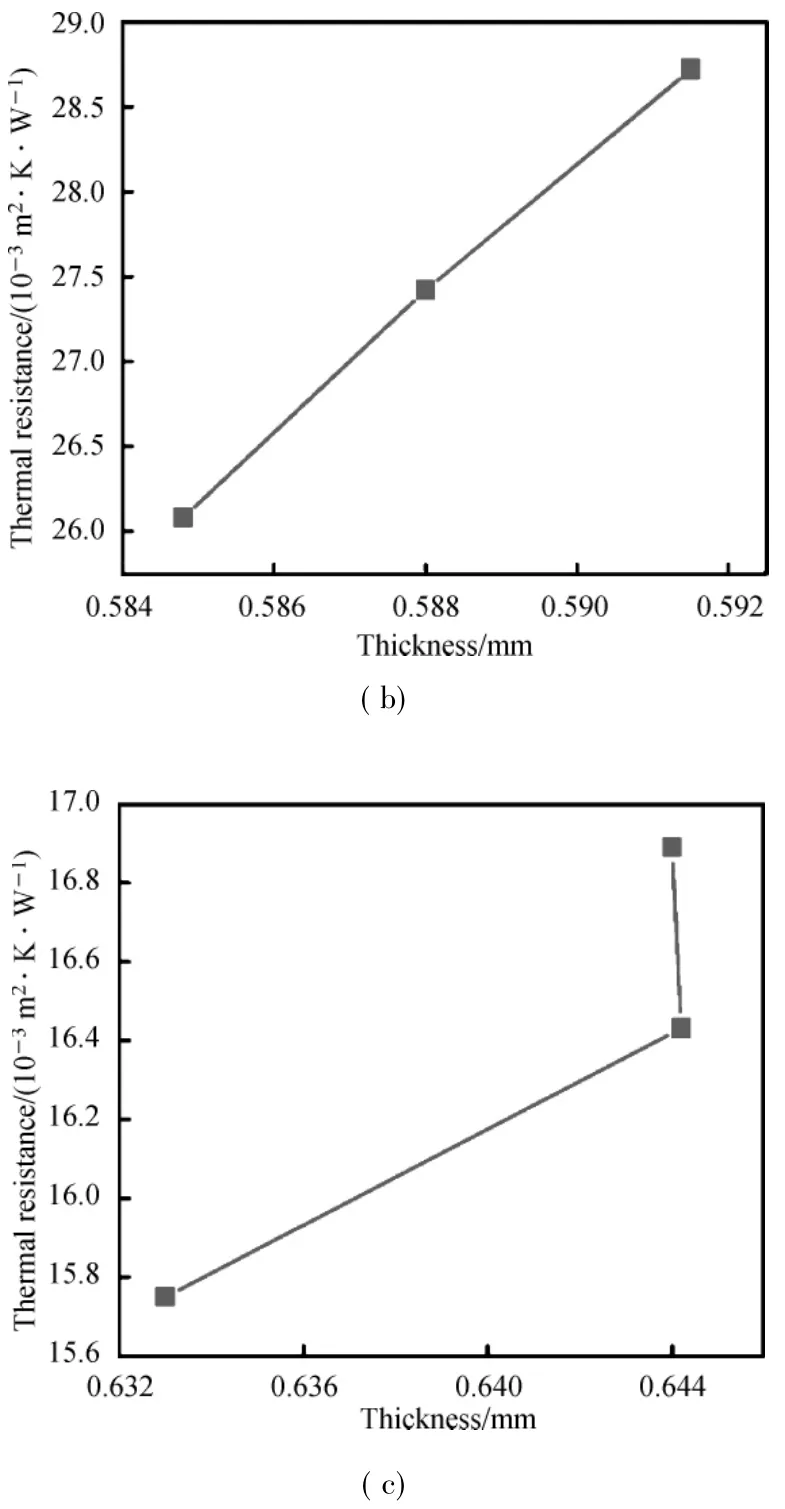
Fig.3 Influence of thickness on the thermal resistance:(a) cotton/kapok blended fabrics with yarn size 18.5 tex,(b)cotton/kapok blended fabrics with yarn size 14.8 tex,and(c)cotton/modal blended fabrics,with yarn size 14.8 tex
Thus the comparative analysis wasmade among the fabrics types.From Table4,it could be seen that themass per square of cotton/kapok blended fabrics was lighter and their thermal resistance was higher than those of cotton/model blended fabric. The achievable reason is that the kapok fiber has special cross section area with oval to round,and high bulkiness.There is large hollow structure as high as 80%-90%of fiber which condenses the volume quality of fiber and stores a large amount of stationary air.It is concluded thatboth thickness and structural characteristics are affecting the thermal resistance.

Table 4 Thermal resistance of blended knitted fabric
3.2 Water vapor resistance
When the fabrics have low rate of water vapor resistance,the water vapor can pass easier through the fabric and to the environment,followed by drier skin.By thismeans it leads to improving body com fort.Table 5 displays the water vapor resistance valueswhich are very close to each other and have no difference between cotton/kapok and cotton/modal blended fabrics.This indicates that the cotton/kapok and cotton/modal blended knitted fabrics have quite good vapor transmission property.
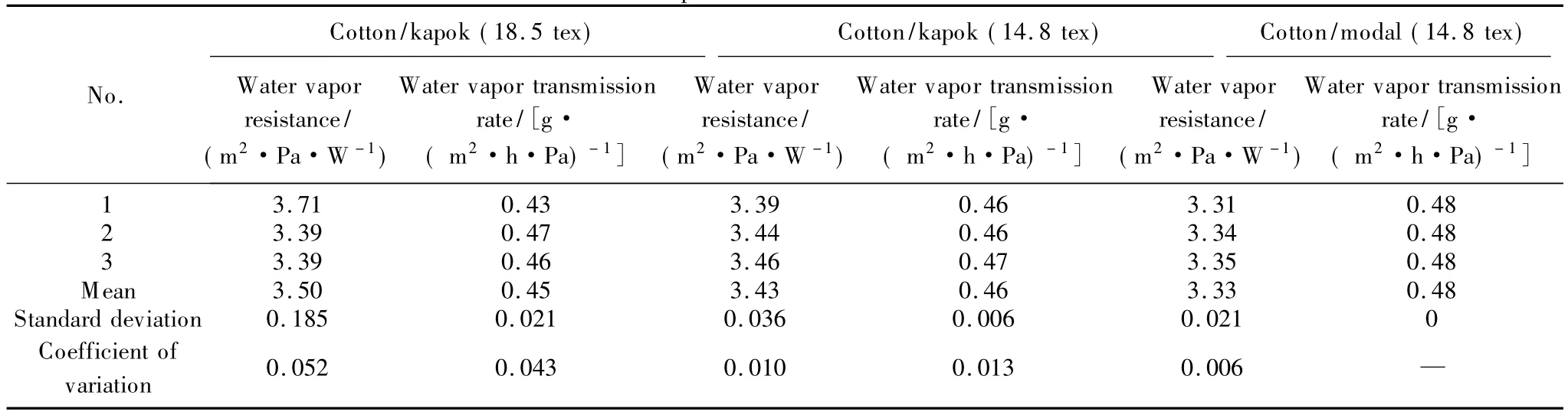
Table 5 Water vapor resistance of blended knitted fabrics
3.3 Verticalw icking
The relationships between the w icking length and the time of cotton/kapok blended fabrics are shown in Fig.4.From Figs.4(a)and(b),the w icking length of cotton/kapok blended fabric yarn size is 18.5 tex and the dye concentration are 0.5%and 1.0%,respectively,and their w icking lengths have linear correlation with the time.The w icking length increases with time increase.Therefore,w icking property in longitudinal direction is better than that in traverse direction. Themost important reason for this observable fact is that the tension in longitudinal direction is high during the knitting process so that capillary is noteasy to be infertile or collapse for the deformation and bending of yarn.As a result the wet conductivity in longitudinal direction is higher than that in traverse direction.From Figs.4(c)and(d),with dye concentration 0.5%and 1.0%,respectively it is observed that both the w icking lengths have linear correlation with the time. Thus,the w icking length increases with the time increase and better w icking property is observed in two directions than those in Figs.4(a)and(b).In general,the natural fibers have bulky hydrophilic group(hydroxyl groups).Compared with cotton fiber,kapok blended fabrics have better water transmission properties.Kapok fiber has larger interior porosity,more loose structure,and lower crystalline degree.As a result,kapok fiber has exhibited bettermoisture absorption.Thus,the liquid water conductivity essentially depends on w icking length.
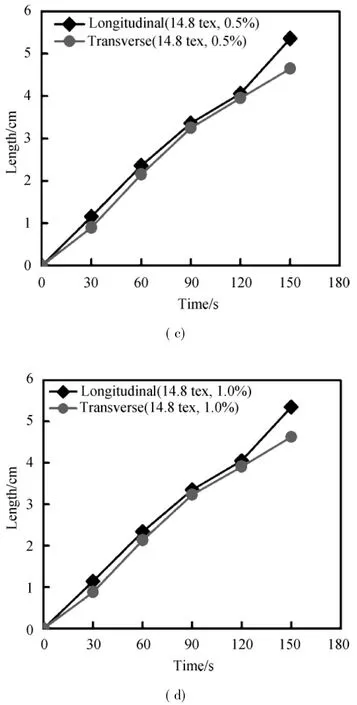
Fig.4 Relationship between verticalwicking lengths vs.time
3.4 Pilling properties of the fabrics
Fabric surface pilling is the result from a dynamic balance between two conflicting impacts,pill wearing off and pill formation.Pilling is produced by fabrics formed from spunyarns(yarns made from staple fibers).Figure 5 shows the pilling results of all cotton/kapok and cotton/modal blended fabric with 125,500,1 000,2 000,5 000 and 7 000 pilling rubs.From Fig.5,the pilling grade for each fabric type decreases gradually with the increase of the pilling rubs.It is due to the decreasings of the extension at break and breaking tenacity,which create the pills easily to be pulled off during the abrasion action.The pilling grades are rated by photographic and visual description standards in an evaluation cabinet under daylight lighting from 1 to 5 in a dark room according to ISO 12945-2:2000,Modified Martindale Method.The pilling standards used for evaluation of the fabrics have the follow ing scales,5 is no pills,4 is slight pilling,3 ismoderate pilling,2 is severe pilling and 1 is very severe pilling.According to the results,all samples in Fig.5(c)at125 rubs have no pills and all samples in Figs.5(a)and(b)have the same pilling rate (themaximum 2.5 with 125 rubs).For the comparison of the fabric types,it is indicated that the cotton/modal blended fabric has better pilling grade than cotton/kapok blended fabrics.This is due to the configuration of kapok fibers,such as short length and smooth surface of the fibers,causing poor inter-fiber cohesion.These defects have prohibited kapok from being processed by modern spinning machines.Also the spun yarns,causing yarn hairiness on the surface of the fiber,yarn hairiness or projecting fibers,are free fiber ends forming fabric surface fuzziness that then develop into pills.Thus,an increase in yarn hairiness leads to a higher propensity for pill formation.It was concluded that the cotton/kapok blended knitted fabrics had pilling grade almost between moderate and severe pilling at the m inimum rubs.
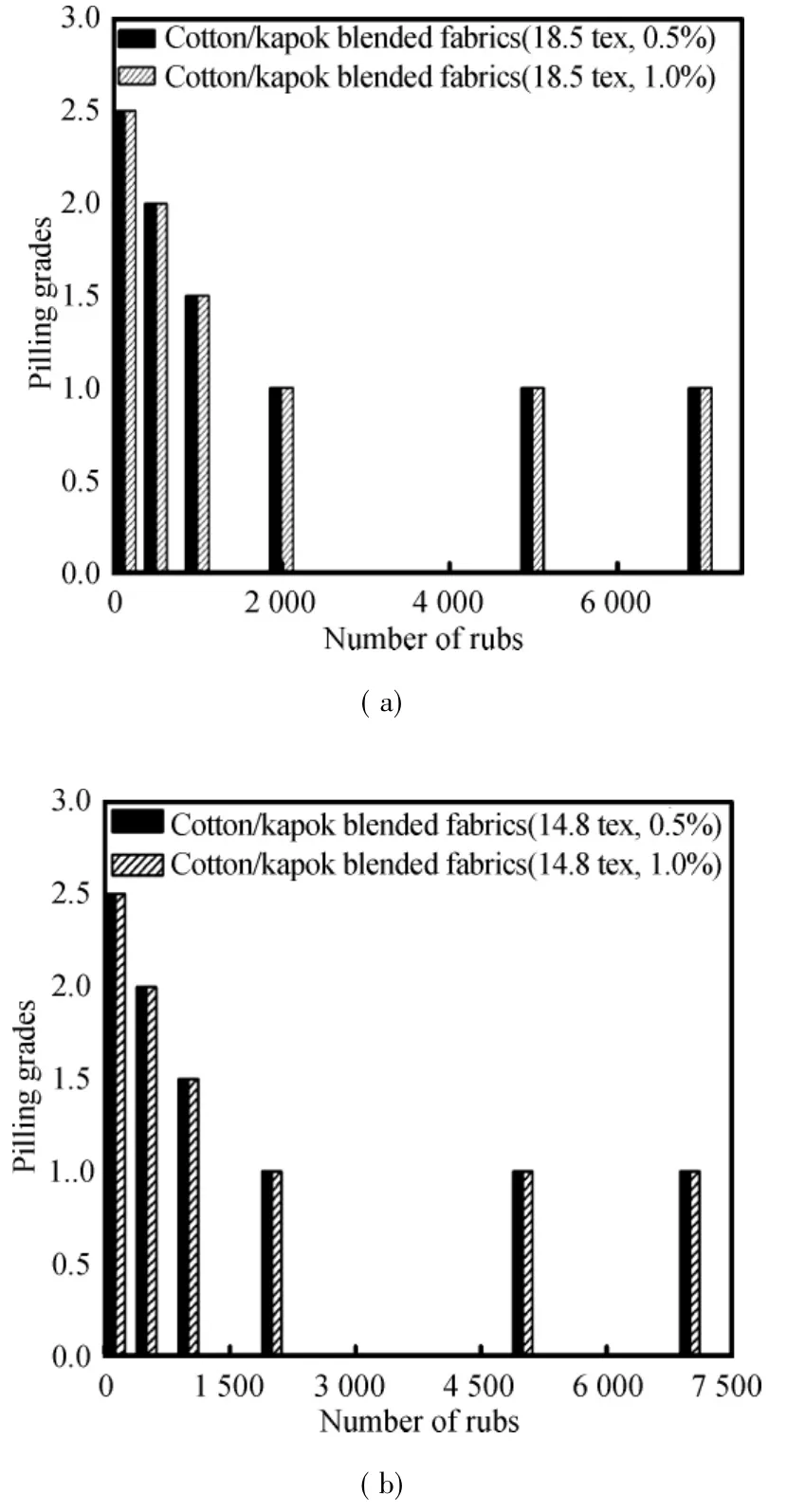

Fig.5 Pilling properties of blended fabrics
3.5 Surfacemorphology of cotton/kapok knitting fabric
In order to estimate the wet chem ical process effect on surface morphology,cotton/kapok blended fabric surface structure has been exam ined by SEM.Figures 6(a)and(d) show the small scales in themicrograph untreated cotton/kapok blended fabrics.It is observed that the surface morphology of fiber has poor tw ist,thus leads to poor cohesion between the fibers as shown in Figs.6(b),(c),(e)and(f).The same scales in the cotton/kapok blended fabrics have being treated with scouring,bleaching,dyeing and finishing.After a period of wear,this processing causes a lot of fluffy in the surface of the fabric,along with the electrostatic interaction;pilling on surface of the fabricswill affect the appearance and com fort.In addition,kapok fiber hasmore poor resistance to alkali than that of cotton fiber,and highmass concentrationsof NaOHmay lead to ribbed serrated surface for kapok fiber.

Fig.6 Surfacemorphologies of cotton/kapok blended fabrics before and after treatment
4 Conclusions
In this research,the com fort properties of single jersey blends fabrics made from yarn 80/20 cotton/kapok with two types of size,18.5 and 14.8 tex as underwear have been investigated and then compared with 50/50 cotton/modal blended fabric of14.8 tex.The orthogonalarray L9(34)isused to determine the optimal condition to treat the fabric tomeet the demand of thermal underwear.Based on the overall evaluation of the results,1.4%,8.0%,2.0%and 1.0%have been selected for concentrations of NaOH,H2O2,Na2SiO3and S.A. A,respectively as the optimum level.
It is found that cotton/kapok blended fabrics have good thermal resistance and the rate of thermal resistance is significantly higher than that of cotton/modal blended fabrics. In contrast to water vapor resistance,it is almost similar and no more difference between cotton/kapok and cotton/modal blended fabrics have been observed.Therefore,the cotton/ kapok and cotton/modal blended knitted fabrics have less breathable air to vapor transmission.Also thew icking length of cotton/kapok blends fabrics increases with testing time increasing.Meanwhile,cotton/modal blended knitted fabrics have better pilling grade than cotton/kapok blended fabrics.It was concluded that cotton/kapok blended fabrics were appropriate for thermal underwear.But the disadvantage of these fabrics is pilling properties.
Acknow ledgements
The authors of this articlew ish to thank the Xiajin Fengrun Textile Co.,Ltd.for spinning the blended yarn.
References
[1]Schindelka B,Litzenberger S,Sabao A.Body Climate Differences for Men and Women Wearing Functional Underwear during Sport at Temperatures below Zero Degrees Celsius[J]. Procedia Engineering,2013,60:46-50.
[2]Li Y.The Science of Clothing Com fort[J].Textile Progress,2001,31(1/2):1-135.
[3]Havenith G.Interaction of Clothing and Thermoregulation[J]. Exogenous Dermatology,2003,1(5):221-230.
[4]Byrne M S,Gardner A PW,Fritz A M.Fiber Types and End-Uses:a Perceptual Study[J].Journal of the Textile Institute,1993,84(2):275-288.
[5]Smith J.The Com fort of Clothing[J].Textiles,1986,15(1): 23-27.
[6]Ruckman JE,Green JA.Com fort of Shirts for Distance Runners[J].Journal of Clothing Tecnology and Management,1995,12: 1-25.
[7]Ghali K,Ghadder N,Harathania J,et al.Experimental and Numerical Investigation of the Effect of Phase Change Materials on Clothing during Periodic Ventilation[J].Textile Research Journal,2004,74(3):205-214.
[8]Önder E,Sarier N.Improving Thermal Regulation Functions of Textiles[C].WTC 4th AUTEX Conference,Roubaix,France,2004.
[9]Bedek G,Salauan F,Martinkovska Z,et al.Evaluation of Thermal and Moisture Management Properties on Knitted Fabrics and Comparison with a Physiological Model in Warm Conditions[J].Applied Ergonomics,2011,42(6):792-800.
[10]Dem iryurek O,Uysalturk D.Thermal Com fort Properties of Viloft/Cotton and Viloft/Polyester Blended Knitted Fabrics[J]. Textile Research Journal,2013,83(16):1740-1753.
[11]Onofrei E,Rocha A M,Catarino A.The Influence of Knitted Fabrics'Structure on the Thermal and Moisture Management Properties[J].Engineered Fabrics and Fibers(JEFF),2011,6 (4):10-22.
[12]Holcombe B V,Hoschke B N.Dry Heat Transfer Characteristics of Underwear Fabrics[J].Textile Research Journal,1983,53 (6):368-374.
[13]Obendorf S K,Smith J P.Heat Transfer Characteristics of Nonwoven Insulating Materials[J].Textile Research Journal,1986,56(11):691-696.
[14]Yan J,Fang C,Wang FM,et al.Compressibility of the Kapok Fibrous Assembly[J].Textile Research Journal,2013,83(10): 1020-1029.
[15]Cui P,Wang F M,Wei A,et al.The Performance of Kapok/ Down Blended Wadding[J].Textile Research Journal,2010,80 (6):516-523.
[16]Xiao H,Yu W D,Shi M W.Structures and Performances of the Kapok Fiber[J].Textile Research Journal,2005,26(4):4-6.
[17]GB/T 11048—2008.Textile Physiological Com fort under Steady-State Conditions Thermal Resistance and Moisture Resistance Measurement[S].Beijing:China Standard Press,2008.(in Chinese)
O175.14
A
1672-5220(2015)04-0613-07
date:2014-04-21
National Natural Science Foundation of China(No.11371087)
*Correspondence should be addressed to YE Hai-ping,E-mail:hpye@dhu.edu.cn
Received date:2014-04-08
Foundation item:Technical Standards for the Development of Kinitted Jinlong Underwear Factory of Guangdong Province,China(No. HX201303000008)
*Correspondence should be addressed to ZHAO Li,E-mail:zhaoli@dhu.edu.cn
猜你喜欢
杂志排行
Journal of Donghua University(English Edition)的其它文章
- Empirical Analysis of Binary Logistic Model for the Influencing Factors of the Chinese Urban and Rural Residents'Woolen Products Consumption—Based on Questionnaires of 513 Urban and Rural Residents in 16 Provinces
- Analysis of Satisfaction with Business Cost in Shanghai Using Structural Equation Modeling Approach
- Ontology Mapping Based on Bayesian Network
- Diurnal and Seasonal Variations in Particulate Matter at Shanghai during the Heavy Haze and Non-haze Periods
- Swept-Volume Display System Based on Cylindrical Space Projection and Curved Reflectors
- Existence of Solutions for Infinity-Point Nonlinear Fractional Boundary Value Problem at Resonance
