Existence of Solutions for Infinity－Point Nonlinear Fractional Boundary Value Problem at Resonance

LIU Rui－juan(刘瑞娟)，JIN Ran(金冉)

1 School of Fundamental Studies，Shanghai University of Engineering Science，Shanghai201620，China

2 College of Information Science and Technology，Donghua University，Shanghai201620，China

Existence of Solutions for Infinity－Point Nonlinear Fractional Boundary Value Problem at Resonance

LIU Rui－juan(刘瑞娟)1，2，JIN Ran(金冉)2

1 School of Fundamental Studies，Shanghai University of Engineering Science，Shanghai201620，China

2 College of Information Science and Technology，Donghua University，Shanghai201620，China

A class of the boundary value problem for fractional order nonlinear differential equation with Riemann-Liouville fractional derivative on the half line was studied．By using the coincidence degree theory due to M awhin and constructing the suitable operators，the existence theorem of at least one solution has been established．An exam ple is given to illustrate our result．

fractional differential equation;infinity-point boundary value problem;coincidence degree theorem;resonance;half line

Introduction

Fractional differential equation can describe many phenomena in various fields of science and engineering such as control，porous media，electrochemistry，viscoelasticity，and electromagnetic.There are a large number of papers dealing with the solvability of nonlinear fractional differentialequations. For details，see Refs.［1－4］and the references therein. References［5－10］considered boundary value problems for fractional differential equations.Recently，various types of multi－point boundary value problems for fractional differential equations at resonance on a bounded domain have been analyzed by Kosmatov［5］，Jiang［6］，Bai［7］，Baiand Zhang［8－9］.

However，there are few papers which consider the boundary value problem at resonance for infinity－pointnonlinear fractional equation on a half line.The follow ing fractional differential equation at resonance with multi－point boundary value problem on a half－line was discussed in Ref.［10］:

where1＜α≤2，η＞0，f:［0，+∞)××→is an SCarathéodory function，andis the standard Riemann－ Liouville fractional derivative.

Enlightened by the literatures above，in this paper，we study the existence of solutions for the follow ing fractional differential equations at resonance with infinity－point boundary value problem on an unbounded domain:

where 1＜α≤2，0＜η1＜η2＜…＜ηi＜…，f:［0，+∞)××→is an SCarathéodory function，andis the standard Riemann－ Liouville fractional derivative.Moreover，we suppose the follow ing resonance condition:

This condition leads that the fractional differential operatorin Eq.(1)has a nontrivial kernel:

The boundary value problems(1)with such critical condition (2)is so－called problems at resonance.Our main tool is the well－known coincidence degree of Mawhin［11］.

1 Prelim inaries

First，Let us briefly recall some notations and an abstract existence result.

Assume Y and Z are Banach spaces，L∈B(Y，Z)，then L is called a Fredholm mapping，if the follow ing conditions are satisfied:(1)Im L is a closed subset of Z;(2)dim Ker L＜+∞;(3)co dim Im L＜+∞.We set the index of L ind L= dim Ker L－co dim Im L，if dim Ker L=co dim Im L＜+∞，then L is called a Fredholm mapping of index zero.And if L isa Fredholm mapping of index zero，there exist linear continuous projectors P:Y→Y and Q:Z→Z such that Im P=Ker L，Ker Q=Im L，and Y=Ker L⊕Ker P，Z=Im L⊕Im Q.Then it follows that L|domL∩KerP:dom L∩Ker P→Im L is invertible. We denote the inverse of this map by KP:Im L→dom L∩Ker P.The generalized inverse of thismap is KP，Q:Y→dom L∩Ker P，KP，Q=KP(I－Q).

Assume L:dom L⊂Y→Z is a Fredholm mapping，ifΩis an open bou－nded subset of Y，the map N will be called L－compact onΩif QN:Ω→Z is bounded and KP，QN:Ω→Y is compact.For Im Q is isomorphic to Ker L，there exists an isomorphism JNL:Im Q→Ker L．

Themain toolwe used is Theorem 2.4 of Ref.［11］.

Theorem 1［11］Assume－L is a Fredholm mapping of index zero and N is L－compact onΩ，whereΩis an open bounded subset of Y.Suppose the follow ing conditions are satisfied:

(1)Ly≠λNy for each(y，λ)∈［(dom LKer L)∩∂Q］×(0，1);

(2)Ny∉Im L for each y∈Ker L∩∂Q;

(3)deg(JNLQN|KerL，Ω∩Ker L，0)≠0，where Q:Z→Z is a continuous projection as above with Im L=Ker Q and JNL:Im Q→Ker L is any isomorphism.

－Then the equation Ly=Ny hasat leastone solution in dom L∩Ω.

For convenience，we introduce some necessary definitions and resultswhich will be used in the article.

Definition 1［2］The fractional integral of orderα＞0 of a function f:(0，∞)→is given by

provided the right side is pointw ise defined on(0，+∞)．

Definition 2［2］The fractional derivative of orderα＞0 of a function f:(0，+∞)→is given by

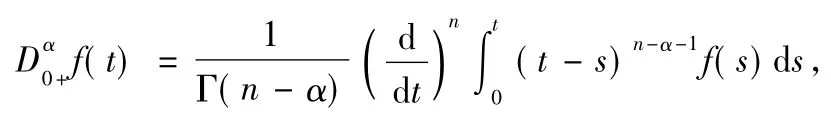
where n=［α］+1，provided the right side is pointw ise defined on(0，+∞).

Lemma 1［2］Assume x∈C(0，+∞)∩Lloc(0，+∞)．Then

where ci∈R，i=1，2，…，n，n=［α］+1．

In this paper，we use the space X，Y defined by

+→［1，+∞)is a continuous strictly increasing function with g(0)=1，g(t)→+∞as t→+∞．Denote‖x‖1=‖x/g‖∞．By standard argument，we can prove that space (X，‖·‖X)(Y，‖·‖Y)are two Banach spaces.

We suppose the following conditions hold:

(H1)exists.

(H2)f:satisfy the SCarathéodory condition，that is，

(2)for a．e．t∈［0，+∞)，(u，v)→f(t，u，v)is continuous on2;

(3)for each r＞0，there existsφr(t)∈L1［0，+∞)∩BC［0，+∞)satisfyingφr(t)＞0，t∈(0，+∞)such that max{‖u‖，‖v‖}≤r implies

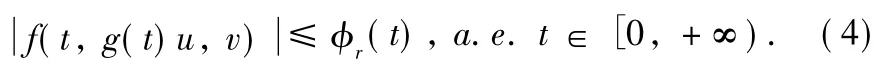
By(H1)，there exists constant M＞0 such that

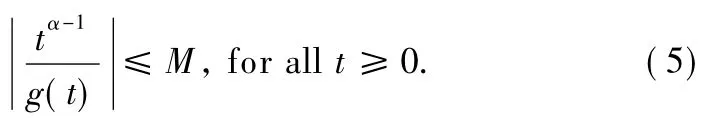
Lemma 2［12］Let D be a subset of Banach space(C［0，+∞)，‖x‖1)．

Then D is relatively compact in(C［0，+∞)，‖x‖1)，if and only if the follow ing conditions are satisfied:

(1)all functions from D are uniform ly bounded;

(2)all functions from D are equicontinuous on any compact interval of J;

(3)all functions from D are equiconvergent at infinity，that is，for any givenε＞0，there exists a T=T(ε)＞0 such that it holds

2 Main Results

In this section，we will establish the existence theorem for the sequential fractional differentialequation involving Riemann－Liouville fractional derivative.In order to prove our main results，we need turn the boundary value problem(1)to operator equation.

Define operator L:dom L∩X→Y as follows:

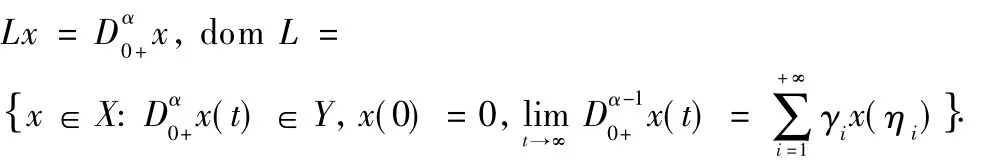
We define N:X→Y be setting N(x(t))=f(t，x(t)，

We also define the linear projector operator Q:Y→Y as follows

whereω(t)∈Y satisfiesω(t)＞0 andω(s)d s=1．It should be pointed that the definition of Q makes sense since y∈L1(0，+∞)∩BC(0，+∞)，then

Lemma 3The operator L:dom(L)⊂X→Y is a Fredholm operator of index zero.The linear operator KP:Im L→dom L∩Ker P→Y can be w ritten as

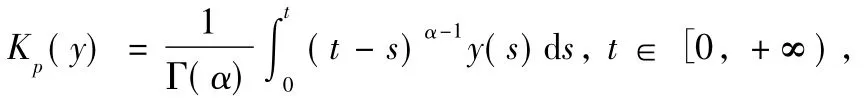
also

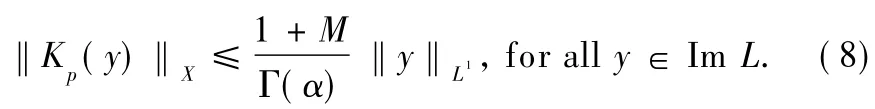
ProofIt is trivial fact thatKer L={ctα－1，c∈R}．Now we show that

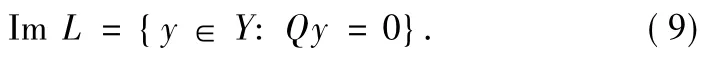
Actually，on one hand，let y∈Im L，there exists x∈Dom L such that y(t)=ByLemma 1，=x(t)+From the condition of the boundary value problem(1)，we have

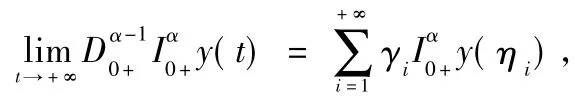
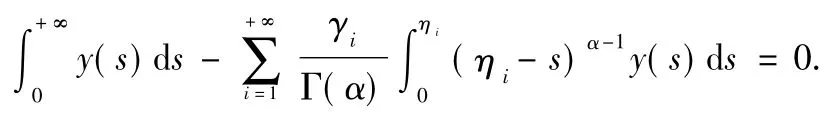
and thus On the other hand，suppose y∈Y satisfies Qy=0．Setting x(t)yields

By Qy=0，we know that

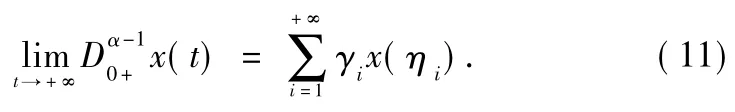
It follows from Eqs.(10)and(11)that x∈dom L andThat is to say，Eq.(9)holds.

For y∈Y，taking the projector Q:Y→Y as follows:

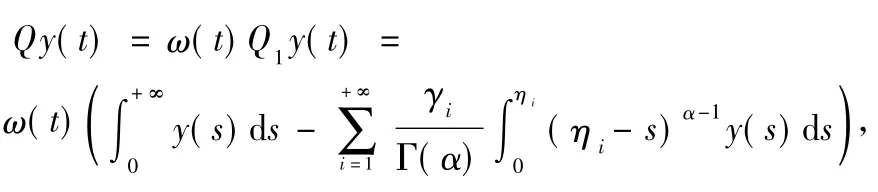
Actually，from Q1ω(t)=1，a simple computation shows that Q is a projector.Denote=y－Qy．It is easy to see that

It follows from Eqs.(9)and(12)that∈Im L and thus Y= Im L+Im Q．By y∈Im Q，there exists constant c∈such that y=cω(t)，and by y∈Im L，Eq.(9)and Q1ω(t)=1，we obtain

This implies that Im L∩Im Q={0}and Y=Im L⊕Im Q．Thuswe have

which implies that L is a Fredholm operator of index zero.

Taking P:X→X as follows:

then the generalized inverse KP:Im L→dom L∩Ker P can be w ritten by

Actually，for y∈Im L，we have

and for x∈dom L∩Ker P，we know

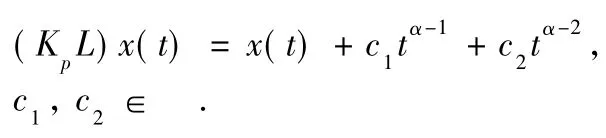
It follows from x∈dom L∩Ker P，Together with Eq.(2)，we get that c1=c2=0 which shows (KpL)x(t)=x(t)．Therefore，

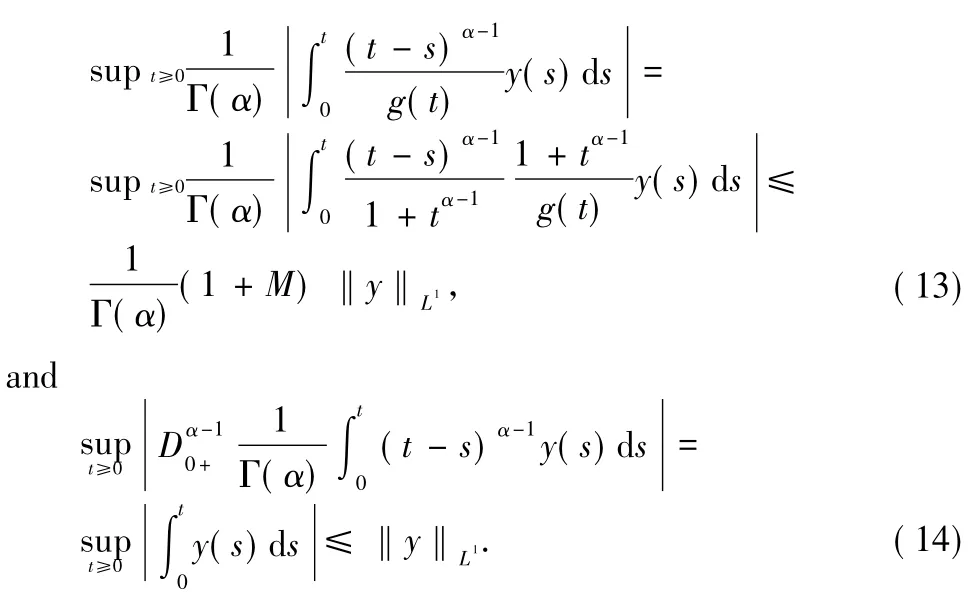
This combined with Formula(13)yields Formula(8).This completes the proof.

Lemma 4Let H2hold，then N is L－compact.

ProofObviously，QN and Kp(I－Q)N are continuous. So we only need to prove that QN and Kp(I－Q)N map bounded sets into relatively compact ones.

Suppose U is a bounded subsetof X，then there exists r＞0 such that‖x‖X≤r for all x∈U and from(H2)，we have

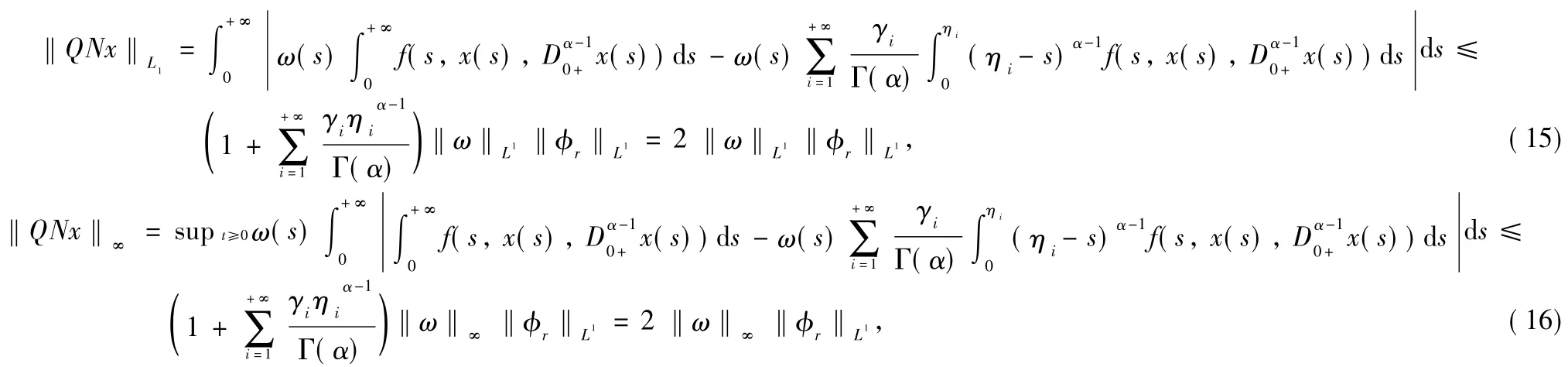
It follows from Formulas(15)and(16)that‖QNx‖Y≤2‖ω‖y‖φr‖L1．Noting that Im Q=2，we get QN is compact.Furthermore，for all x∈U，we have

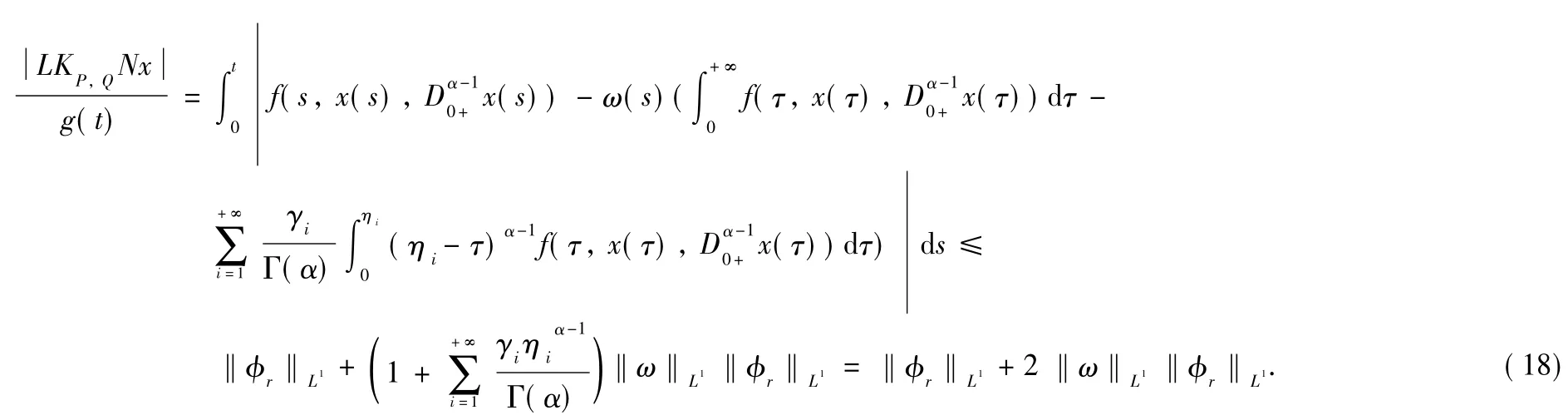
It follows from Formulas(17)and(18)that KPQNU is uniform ly bounded.Meanwhile，for any fixed T＞0，and for any 0≤t1＜t2≤T，

Therefore，by Formulas(19)and(20)，KP，QNU is equicontinuous.By Lemma 2，we can see that if KP，QNU/g(t)and LKP，QU are equiconvergent at infinity，then KP，QNU is relatively compact in X.In fact，considering the follow ing estimate

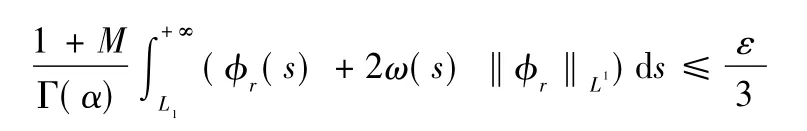
holds forε＞0 and some L＞0，where M is defined in Formula

(5).By(H1)，we suppose that=a．Then we have

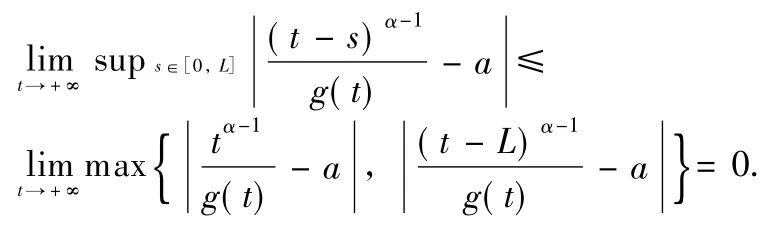
Thus，there exists T＞L such that for t≥T，

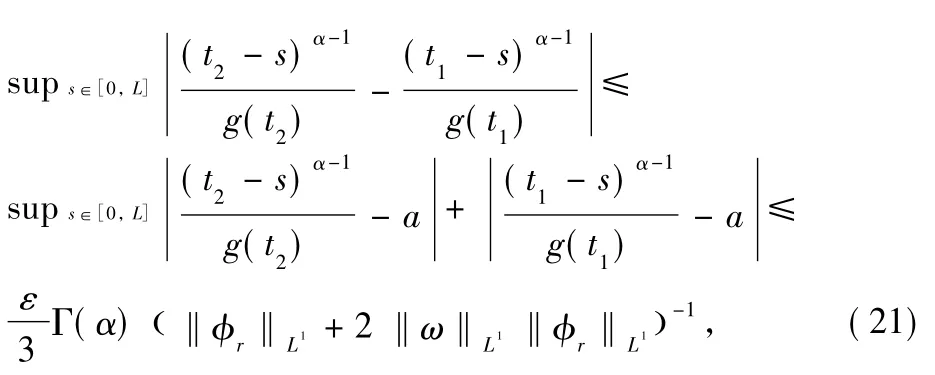
Therefore，for t1，t2≥T，we get

So we complete the proof.

Theorem 2 Let the hypothesis(H2)hold and the follow ing conditions are satisfied.

(1)There exist functions a，b，c∈L1［0，+∞)，c≠0，such that

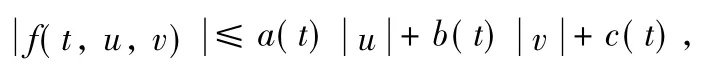
(2)There exists constant A1＞0 such that for x∈dom L， if for all t≥0，then

(3)There exists constant A2＞0 such that for any c∈，either

or else

Then the boundary value problem(1)has at least one solution in space X provided that

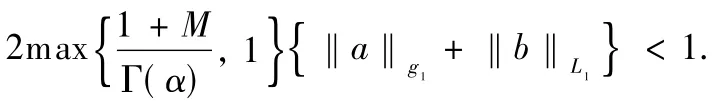
ProofWe construct an open bounded setΩ⊂X that satisfies the assumption ofTheorem 1.Let

Ω1={x∈dom LKer L|Lx=λNx，for someλ∈［0，1］}．

For x∈Ω，we have x∈Ker L，λ≠0 and Nx∈Im L，then Ker Q=Im L．Thus Q(Nx)=0.By(2)ofTheorem 2，we know that there exists t∈［0，+∞)such that

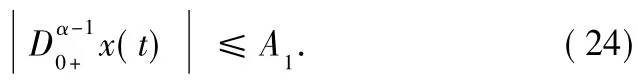
It follows from the identityd s thatwe have

Again by x∈Ω，x∉Ker L，then(I－P)(x)∈Dom L∩Ker P and LP(x)=0，thus from Lemma 3，we have

where C=max By Formulas(25)－(26)and hypothesis(H1)，we have

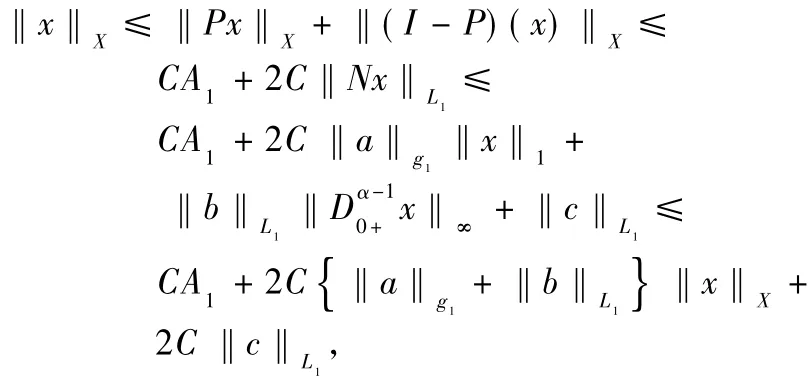
which implies that is， Ωis bounded.

LetΩ2={x∈Ker L:Nx∈Im L}．For x∈Ω2，x∈Ker L implies that x=ctα－1，where c is an arbitrary constant. Since QN(x)=0，

where Q is defined in Eq.(6).By the condition(2)ofTheorem 2，we getc≤A2，which impliesΩ2is bounded in X.

Define the isomorphism J:Im Q→Ker L as follows: J(cω(t))=ctα－1，c∈．

If the first part of condition(3)inTheorem 2holds，we set

For any x=ctα－1∈Ω3，one hasλ(cω(t))=λJ－1(x)= (1－λ)QNx．Ifλ=1，then c=0 and，ifc＞A2，by the condition(3)，it hasλc2ω(t)=(1－λ)ω(t)cQf(t，ctα－1，which contradictsλc2ω(t)＞0．If other parts of the condition(3)hold，we take

and again，we obtain a contradiction.Thus，in either case

that is，Ω3is bounded.

SetΩbe an bounded open set such thatΩIt follows fromLemmas 3and 4 that L is a Fredholm operator of index zero and N is L－compactonΩ.By the definition ofΩandTheorem 1，it is sufficient to prove Eq.(3)ofTheorem 1is satisfied.To this end，let H(x，λ)=±λI d x+(1－λ)JQNx，where Id is the identical operator.By virtue of the definition ofthen by the homotopy property of degree，we obtain that

Thus，Eq.(3)of Theorem 1 is fulfilled and Lx=Nx has at least one solution in dom L∩∂Ω．．The proof is complete.

3 Exam ple

Consider the boundary value problem

Taking A1=3，for any x∈X，assuming thatholds for t∈［0，+∞)，then

The condition(2)ofTheorem 2holds.

It is easy to see that all c＞0，we have

We also can prove that if c＜0，there is cQf(t，ctα－1，tα－1)＞0．The condition(3)ofTheorem 2is satisfied withc＞4．So the boundary value problem(1)has at least one solution.

4 Conclusions

In this paper，by using the coincidence degree theory due to Mawhin and constructing the suitable operators，we obtain the existence result for infinity－point boundary value problem at resonance of nonlinear fractional differential equation.An example is presented to illustrate the result.

［1］Hilfer R.Applications of Fractional Calculus in Physics［M］. Singapore:World Scientific，2000.

［2］Kilbas A A，Srivastava H M，Trujillo J J.Theory and Applications of Fractional Differential Equations［M］. Netherlands:Elsevier B.V.，2006.

［3］Lakshmikantham V，Leela S，Vasundhara J.Theory of Fractional Dynam ic Systems［M］.Cambridge，UK:Cambridge Academ ic Publishers，2009.

［4］Miller K S，Ross B.An Introduction to the Fractional Calculus and Differential Equations［M］.New York:John Wiley，1993.

［5］Kosmatov N.A Boundary Value Problem of Fractional Order at Resonance［J］.Electronic Journal of Differential Equations，2010 (135):1－10.

［6］Jiang W H.The Existence of Solutions for Boundary Value Problems of Fractional Differential Equations at Resonance［J］. Nonlinear Analysis，2010，doi:10.1016/j.na.2010.11.005.

［7］Bai Z B.On Solutions of Some Fractional m－point Boundary Value Problems at Resonance［J］.Electronic Journal of Qualitative Theory of Differential Equations，2010(37):1－15.

［8］Bai Z B，Zhang Y H.The Existence of Solutions for a Fractional Multi－point Boundary Value Problem［J］.Computers and Mathematicswith Applications，2010，60(8):2364－2372.

［9］Zhang Y H，Bai Z B.Existence of Solutions for Nonlinear Fractional Three－Point Boundary Value Problems at Resonance［J］.Journal of Computational and Applied Mathematics，2010，doi:10.1007/s12190－010－0411－x.

［10］Zhou H C，Kou CH，Xie F.Existence of Solutions for Fractional Differential Equations with Multi－point Boundary Conditions at Resonance on a Half－Line［J］.Electronic Journal of Qualitative Theory of Differential Equations，2011(27):1－16.

［11］Mawhin J.Topological Degree Methods in Nonlinear Boundary Value Problems［C］.NSFCBMS Regional Conference Series in Mathematics，American Mathematical Society，Providence，RI，USA，1979.

［12］Agarwal R P，Regan D O.Infinite Interval Problems for Differential，Difference and Integral Equations［M］.Dordrecht: Kluwer Academ ic Publishers，2001.

［13］Jiang W H，Huang X Q，Wang B.Boundary Value Problems of Fractional Differential Equations at Resonance［J］.Physics Procedia，2012，25:965－972.

［14］Zhang S Q，Hu L，Shi A L.Existence Result for a Nonlinear Fractional Differential Equation with Integral Boundary Conditions at Resonance［J］.Advances in Difference Equations，2013，353，doi:10.1186/1687－1847－2013－353.

［15］Chen F L，Zhou Y.Existence Theorem for a Fractional Multipoint Boundary value problem［J］.Fixed Point Theory，2014，15 (1):43－58.

［16］Liu R J，Kou C H，Xie X J.Existence Results for a Coupled System of Nonlinear Fractional Boundary Value Problems at Resonance［J］.Mathematical Problem in Engineering，2013，doi:10.1155/2013/267386.

［17］Hao X H，Zhou Z F.The Existence of Solutions to a Class of Multi－point Boundary Value Problem of Fractional Differential Equation［J］.Journal of Mathematical Research with Applications，2013，33(2):175－188.

O175.8

A

1672－5220(2015)04－0665－07

date:2014－08－18

National Natural Science Foundation of China(No.11271248)

*Correspondence should be addressed to LIU Rui－juan，E－mail:ruirui0516@163.com