Ontology Mapping Based on Bayesian Network
2015-08-07ZHANGLingyu张凌宇TAOBairui陶佰睿
ZHANG Ling-yu(张凌宇),TAO Bai-rui(陶佰睿)
Computer Center,Qiqihar University,Qiqihar 161006,China
Ontology Mapping Based on Bayesian Network
ZHANG Ling-yu(张凌宇)*,TAO Bai-rui(陶佰睿)
Computer Center,Qiqihar University,Qiqihar 161006,China
Ontology mapping is a key interoperability enabler for the semantic web.In this paper,a new ontology mapping approach called ontology mapping based on Bayesian network(OM-BN)is proposed.OM-BN combines the models of ontology and Bayesian Network,and applies the method of M ulti-strategy to com puting sim ilarity.In OM-BN,the characteristics of ontology,such as tree structure and semantic inclusion relations among concepts,are used during the process of translation from ontology to ontology Bayesian network(OBN).Then the method of M ulti-strategy is used to create sim ilarity table(ST)for each concept-node in OBN.Finally,the iterative process of mapping reasoning is used to deduce new mappings from STs,repeated ly.
component;ontology mapping;multi-strategy;Bayesian networkmodel
Introduction
Ontology mapping is to create semantic relations between elements that are from different ontologies,and three main elements are contained in ontology,i.e.,concepts,relations and instances.Both of relations and instances are used to represent concepts,and we can consider concepts as the basic elements of ontology.Therefore,calculation of concept similarity becomes a key step in ontology mapping.There are many different methods to compute concept similarity:the systems of GLUE and LSD,provided by Doan,create ontology mapping using machine learning techniques in Refs.[1-2]. Madhavan et al.[3]proposed amapping method named Cupid,which is a hybrid matcher based on both element-level and structure-levelmatching.Bayesian network(BN)is applied to ontology mapping in Refs.[4-7].However,the approaches in Refs.[1-3]did not consider how to effectively choose multi-strategies to decrease the calculation of similarity. Although the methods in Refs.[4-7],excessively concentrated on the technique of BN,they ignored the characteristics of ontology,such as tree structure and semantic inclusion relations among concepts.
In this paper,we present a new approach of ontology mapping called ontology mapping based on BN(OM-BN). During the process of ontology mapping in OM-BN,we firstly use the characteristics of ontology,i.e.,tree structure and semantic inclusion relation among concepts,and translate ontology into BN.Here we name the translated BN as ontology BN(OBN)to distinguish with the traditional BN.Then we make use of themethod of themulti-strategy to create similarity table(ST)for each concept-node in OBN.Finally we use the iterative process ofmapping reasoning to deduce new mappings from the similarities of ST,repeatedly.
1 Related Works
At present,there are a great many of approaches for ontology mapping.For example,Jean-Mary and Kabuka[8]provided an algorithm of ontology mapping ASMOV,which useed lexical information,external information,internal information,and individual information.Tang et al.[9]proposed the ontology mapping model of risk m inim ization based ontology mapping(RiMOM)whose risk function was created by the Multi-strategy,such as name-based strategy,instance-based strategy,and description-based strategy.Asooja and Gracia[10]provided an ontology mapping system called monolingual and cross-lingual ontology matching(CIDERCL),and it computed sim ilarities for concept-pairs by comparing their context including linguistic description,axioms,related terms,etc.Kuo and Wu[11]proposed a Multistrategy ontology mapping system open data group ontology matching system(ODGOMS),in which the string-based and token-based strategies were exploited to create the mappings. Fang et al.[12]provided a mapping method for biomedical ontologies based onmultiple sim ilarity methods.Other classical systems for ontology mapping,such as GLUE[1],Cupid[3],combination of schema matching approaches(COMA)and Rahm[13],S-Match[14],and CIQ[15],also adopted the multistrategy method to createmappings for concepts.
In addition,some researches on applying BN to ontologies mapping have been done.The most typically method is provided by M itra et al.[6].It introduced BN into ontology mapping and proposed ontology mapping enhancer(OMEN),which is a framework to probabilistically improve existing ontology mappings.In OMEN,the mapped concept-pairs are converted into nodes,and the edges of BN are formed by the relationships among concepts.Finally,“Meta-rules”proposed by OMEN are used to reason other new mappings.
In recent years,the researches on ontology mapping have attached much attention,and many methods are provided. Zhang et al.[16]proposed a method called fuzzy ontoloyy mapping based on conceptual graph(FOM-CG)based on conceptual graph,which could be used to create mappings for multiple fuzzy ontologies.Lü[17]combined syntactic sim ilarity with structural similarity to create mappings in an ontology integration process.Tatsiopoulos and Boutsinas[18]translated ontologies to be mapped into association rule bases,and reasoned mapping relationships between them.Tun et al.[19]provided an enrichment-based ontology matching technique (EOM),which improved information for concepts based on philosophical notions,i.e.,identity,rigidity,and dependency.
2 Translating from Ontology to BN
In this section,we will propose the set of transformation rules,which isused to translate ontology to BN.Before presenting the set of transformation rules,we will briefly introduce themodels of ontology and BN.
2.1 Themodels of ontology and BN
Ontology provides a formal and explicit measure todescription domain know ledge,and it plays an important role in information integration and know ledgemanagement.According to Studer et al.[20],ontology is a formal,explicit specification of a shared conceptualization.Conceptualization refers to an abstractmodel of some phenomenon in the world by identifying the relevant concept of that phenomenon.Explicit means that the types of concepts used and the constraints on their use are explicitly defined.Formal refers to the fact that the ontology should bemachine readable(which excludes for instance natural language).Shared reflects the notion that an ontology captures consensual know ledge,that is,it is not private to some individual,but accepted as a group.
Definition 1(Ontology)The formal definition of Ontology is O={C,HC,R,I,A},where
1)C denotes a set of concepts,which are collections of instances(objects)of the domain,representing the basic meanings in the world;
2)HCdenotes a set of taxonomy relations which represent inheritance relationships among concepts,such as“is-subclassof”and“is-supclass-of relations”;
3)R denotes a set of non-taxonomy relations(i.e.,predicate relationships)among concepts;
4)I denotes a set of instances belonging to a given concept;
5)A denotes a set of axioms,formally expressing conditions to be verified by the elements of the ontology in order to guarantee its correctness,and allow ing to infer new know ledge which is not explicitly represented in the ontology.
BN proposed in Ref.[21],also called probabilistic inference network or belief network,is a graphical probability model for representing the probabilistic relationships among a large number of random variables and probabilistic inference with them.BN is composed of a set of nodes and edges.The nodes,or vertices,represent the variables and the edges,or arcs,represent the conditional dependencies among the nodes. Generally speaking,BN is considered as a directed acyclic graph(DAG)thatallows for efficientand effective inference of probability distributions over a set of random variables.Besides the power of probabilistic reasoning provided by BN itself,we are also attracted to BN by the structural similarity between the DAG of a BN and the RDF graph of OWL ontology:both of them are directed graphs,and direct correspondence exists betweenmany nodes and edges in the two graphs.
Definition 2(BN)The formal definition of BN is BN={G,θ},where:
1)G is a directed acyclic graph whose vertices correspond to the random variables X1,X2,…,Xn,and whose edges represent direct dependencies between the variables;
2)θrepresents the set of conditional probability tables (CPTs),each of which specifies the probability of each possible state of the node given each possible combination of states of its parents.
2.2 The set of transformation rules
The process of translating ontology into BN is realized by a translation function(φ).According to the quintuple O={C,HC,R,I,A}which is the formal definition of ontology,the BN translated byφisφ(O)={G=<N,E>,P,I,A,θST},where G is a DAG composed by the set of nodes N and the set of edges E,P and I respectively denote the property set and the instance set of nodes,A represents a set of axioms and θSTdenotes the set of STs which will be fully introduced in the next section.The translated BN is called OBN,because it has many characteristics inherited by ontology.The specific transformation rules are as follows.
1)N=φ(C),i.e.,C,the setof concepts in ontology,is mapped into N,the set of concept-nodes in OBN,and the mapping relationships between concepts and concept-nodes are one-to-one.
2)E=φ(HC),i.e.,HC,the set of hyponymy relationships among concepts in ontology,ismapped into E,the set of edges in OBN.
3)P=φ(R),i.e.,R,the set of non-taxonomy relationships among concepts in ontology,ismapped into P,the set of properties in OBN.
4)I=φ(I),i.e.,I,the set of instances for concepts in ontology,is mapped into I,the set of instances for conceptnodes in OBN.
5)A=φ(A),i.e.,A,the set of axioms in ontology is mapped into A,the set of axioms in OBN.
6)OBN=φ(O),i.e.,amodel of ontology O ismapped into amodel of OBN.
All transformation rules for structure are given by abovementioned rules.In order to label nodes and edges of OBN with probabilities,some important rules for computing probabilities will be provided as follows.
7)P(n)=φ(I(n)),where n∈N denotes a concept-node in OBN,and I(n)denotes the number of instances for n.The functionφ(I(n)),whose result is a ratio of the number of instances of n to the number of all instances,can be used to acquire prior probabilities of concept-nodes.
8)P(B|A)=φ(B,A),where concept-node B is the child-node of concept-node A,andφ(B,A)is used to compute the conditional probability labeling the edge between A and B. For the conditional probability P(B|A),we can fallback on the formula of conditional probability that is P(B|A)=P(AB)/ P(A).In this formula,it is necessary to get two probabilities which are the prior probability P(A)and the joint probability P(AB).P(A)can be gotby the Rule7)easily,but P(AB)is unknown for us.However,the relationship of semantic inclusion between A and B,that is B⊆A or A∩B=B,makes it easily to get the equation P(AB)=P(B).So,the improved formula is as follows:
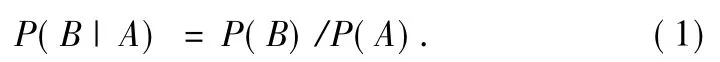
For example,based on the above-mentioned transformation rules,a fragment of an ontology which represents the relationships between teachers and courses in some college can be transformed into a fragment of OBN.The result is shown in Fig.1,in which nodes and edges represent concepts and relationships,respectively.

Fig.1 Themodel of OBN from a fragment of OWL document
We have reason to believe that the proposed transformation rules are complete.To explain it,letus review the relationships between the transformation rules and the formal definition of ontology O={C,R,HC,A,I}.It is easy to find that the five elements in ontology can be mapped into the correspondingelements in OBN using the first five rules,and the mapping relationships are composed by C→N,HC→E,R→P,I→I,and A→A.To sum up,the translation does not cause information loss.
3 Method of OM-BN
In OM-BN,the process of ontology mapping is broken down into threemain steps shown in Fig.2.The first step is the translation from ontology to OBN(shown in section 2.2).The second step is to create ST for each concept-node in OBN.The last step is using the iterative process of mapping reasoning in which new mappings are repeatedly deduced from STs.
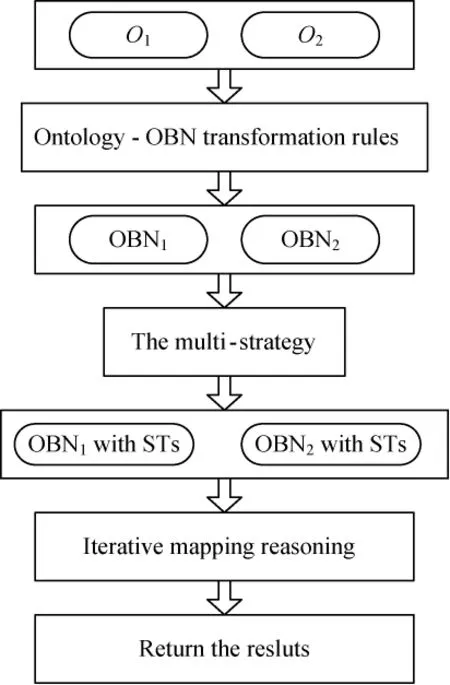
Fig.2 The process of ontology mapping
3.1 Creating sim ilarity tables for all conceptnodes
For the sake of understanding,we divide this process into three sub-steps,i.e.,how to quickly create all correct conceptnode-pairs between two OBNs,how to compute similarities of concept-node-pairs by the multi-strategy,and how to generate STs to store the similarities.
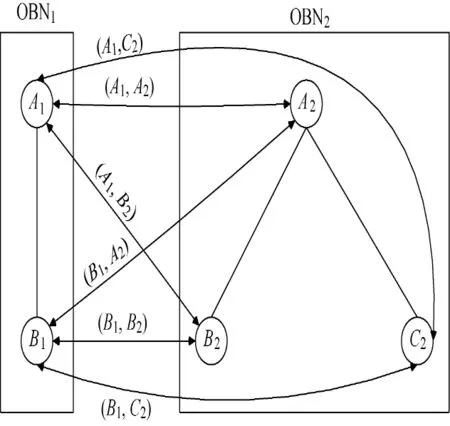
Fig.3 All the concept-node-pairs between OBN1and OBN2
1)How to quickly create all correct concept-node-pairs between two OBNs
Before computing sim ilarities,we should create all the correct concept-node-pairs,in which two concept-nodes do not come from the same OBN.As shown in Fig.3,concept-nodes of A1and B1belong to OBN1,and OBN2includes three concept-nodeswhich are A2,B2,and C2.It is easy tomanually create all the correct concept-node-pairs between OBN1and OBN2.The results obtained by human effort are(A1,A2),(A1,B2),(A1,C2),(B1,A2),(B1,B2),and(B1,C2).When OBN1and OBN2contain a great number of conceptnodes,in otherwords,m and n are very large,it is difficult for us to manually traverse the two OBNs and find all the correct concept-node-pairs.However,the tree structure of OBNs,i.e.,concept-nodes in OBNs are arranged by levels and no cycle will appear in OBNs,makes it easily for us to find all conceptnode-pairs by using many classic traversal algorithms such as depth-first traversal and breadth-first traversal.
2)How to compute sim ilarities of concept-node-pairs by themulti-strategy
In recent years,many ontology mapping systems are based on multi-strategies.Each strategy can only deal with a type of information effectively,and thus it is necessary to combine many different types of strategies to maxim ize sim ilarity accuracy.But using too many strategies will bring out some problems,e.g.,large calculation of similarities and hardship of similarity combination.Hence,the best way is to choose the most appropriate strategies,and avoid using the inefficient strategies.Since the semantics of concept-node is represented by the elementsof name,description,and instance,we can use the follow ing three strategies to get precise similarity of conceptnode-pair.
(1)Name based strategy
Names composed by character strings are human identifiers for concept-nodes,normally shared by a community of humans speaking a common language.Several ideas have already been created to compare names.Levenshtein Distance[22],which is the number of edit operations necessary to transform one string to another one,is a measure of the sim ilarity between two names.The follow ing is the Formula(2)based on name strategy:
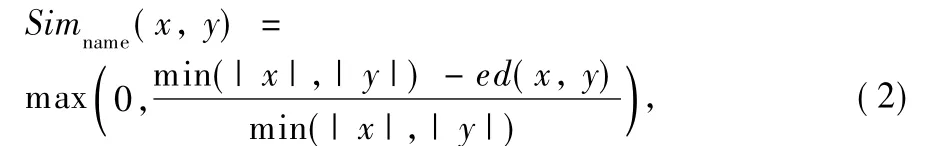
where the symbols of|x|and|y|respectively denote the length of strings x and y,and ed(x,y)indicates the number of edit operations,including deletions,insertions,and substitutions,required to transform x to y.
(2)Description based strategy
Description,which is expressed by natural language,is also one kind of expressive information of concept-nodes. Usually,it representsmore semantics of the concept-node than name itself.We use text classification method to compute similarity of the description between concept-nodes.More specifically,we use word frequencies in concept-node descriptions of the target OBN and construct a Naive Bayesian classifier[23].Then we exploit words in concept-node descriptions of the source OBN for prediction which is equivalent to the similarity.
(3)Instance based strategy
Instance based strategy has the advantage of focusing on the most active parts of the OBNs,and reflects concept-node-pair semantics as they are actually being used.The idea of this strategy is that similarity between the instances of two conceptnode-pairs predicts the semantic similarity of these conceptnode-pairs.The similarity between two concept-nodes can be computed by Jaccard coefficient[1]:

In this formula,the symbolsof x and y denote two conceptnodes,and P(x,y)is the probability that a random ly chosen instance from the universe belongs to both x and y.The denominator of the Formula(3)is the probability that a random ly chosen instance from the universe belongs to either x or y.
(4)Combination
There are two combination approaches which are hybrid and composite[13].The hybrid approach ismost common where differentmatch criteria or properties(e.g.,name and data type)are used within a single algorithm.By contrast,a composite approach combines the results of several independently executed match algorithms.In order to use the results provided by the multi-strategies,we should adopt composite.The follow ing is the Formula(4)which combines the results generated by the three strategies with the corresponding weights:

In this formula,the weights ofλName,λComment,andλInstanceare acquired by many ways,such as neural network,machine learning,and so on,and the relationship of these weights is λName+λComment+λInstance=1.
3)How to generate STs to store the similarities
A new data structure named by ST is introduced to store the similarities acquired by the multi-strategy.Among multiple OBNs,we should firstly consider themost important one as the source OBN,and the remainder ones are all target OBNs.To avoid redundancy computing of similarity,only concept-nodes in the source OBN are allowed to have STs.The ST of each concept-node in the source OBN saves all the similarities between the concept-node itself and other concept-nodes in other target OBNs.The process of obtaining STs consists of two major phases:one is to acquire a similarity list(SL);the other is to generate STs of concept-nodes by decomposing the SL.
(1)Acquiring SL
The SL will be used to save similarities between the concept-nodes in the source OBN and the concept-nodes in the target OBNs.Therefore,we label rows of SL by concept-nodes of the source OBN(A,B,C,…),and the columns are labelled by concept-nodes of target OBNs(A1,B1,C1,…,A2,B2,C2,…).Each cell in SL can be used to record the similarity of corresponding concept-node-pair.
(2)Generating STs from SL
From the SL,we find that rows in the SL are denoted by the corresponding concept-nodes in the source OBN.Therefore,by decomposing the SL by rows,we can generate all the STs of concept-nodes.For example,Table 1 shows the ST of conceptnode A,which contains the similarities between A and all the concept-nodes of the target OBNs.
To sum up,we canmake the bestuse of the characteristics and the internal information of ontology,and create STs for all the concept-nodes in the source OBN.During the process of mapping reasoning,these data are used to deduce mapping relationships between concept-nodes.
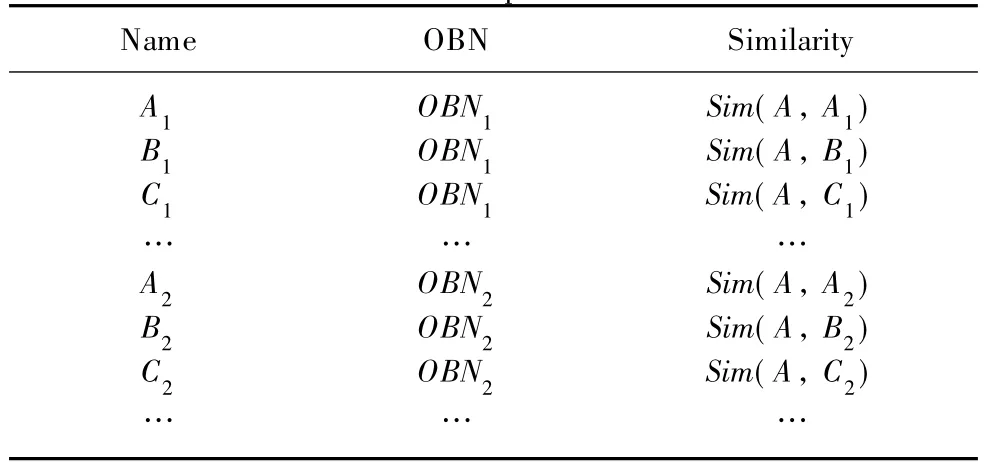
Table 1 The ST of concept-node A in source OBN
3.2 The iterative process ofm apping reasoning
Themeaning ofmapping reasoning is that creatingmapping relationship for the concept-node-pair whose sim ilarity exceeds some threshold.However,themapping reasoning process is not one step but iterative,because some new mappings created by the previous reasoning step will be used to deduce other mappings in the next reasoning step.We will introduce the iterative process of mapping reasoning with an example.The information of source OBN is shown in Fig.4,and Fig.5 shows amapping from A to A',according to the similarity Sim(A,A') which ismore than a given threshold.The final result is shown in Fig.6.
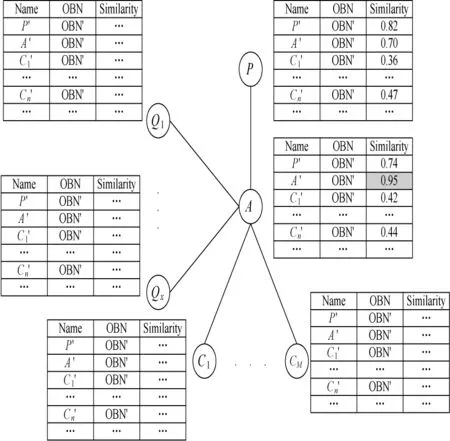
Fig.4 STs in the source of OBN
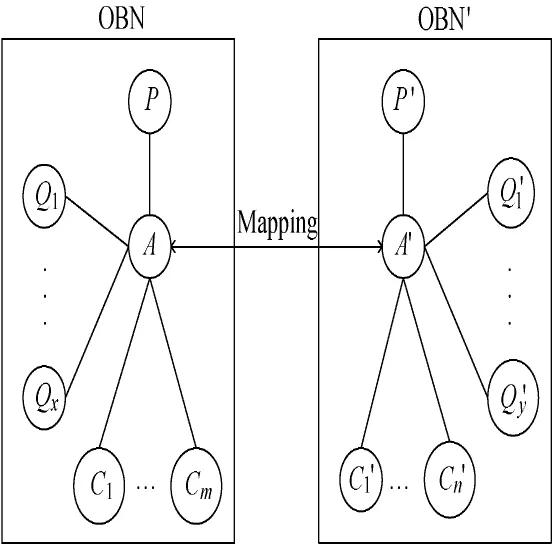
Fig.5 Creating mapping between A and A'
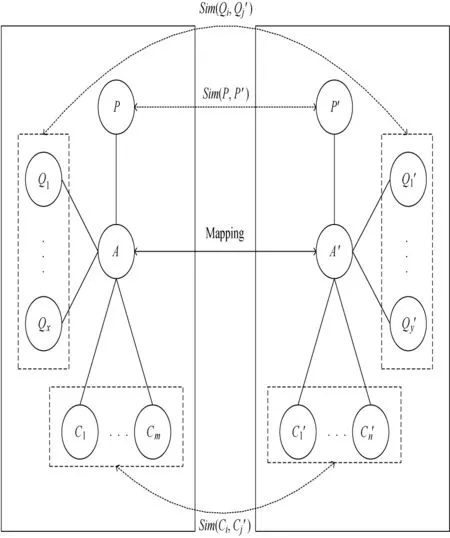
Fig.6 The final result of the iterative process ofmapping-reasoning
1)We will retrieve records in the STs,and find outall the concept-node-pairswhose sim ilarities are equal or greater than the given thresholdδ(0.9).According to different needs,the given thresholdδcan be modified.Then push these conceptnode-pairs into the MappingQueue storing the found conceptnode-pairs temporarily.From the STs of nodes shown in Fig.4,we find the sim ilarity Sim(A,A')is 0.95,which is greater thanδ,and the concept-node-pair(A,A')is pushed into the MappingQueue.
2)Pop a concept-node-pair from the MappingQueue,e.g.,(A,A').Then we create the mapping relationship of Mapping(A,A')and add themapping to the MappedSetwhich restores the created mappings by reasoning.If the MappingQueue is empty,that is to say we can not get any mapping,and then we terminate the iterative process of mapping-reasoning,and return to users the finalmappings of the MappedSet.
3)Creating two adjacent-node sets,i.e.,Set_Nodes and Set_Nodes',for the two concept-nodes in a concept-node-pair (A,A').Then the concept-nodes in Set_Nodes(resp.,Set_Nodes')are classified into three subsets.For example,concept-nodes A and A'are contained in the concept-node-pair (A,A').According to the set of edges E(resp.,E')and the set of properties P(resp.,P'),we can divide Set_Nodes (resp.,Set_Nodes')into three subsets:Set_Parent{P}(Set_ Parent'{P'})is the setof parent-nodes for A(resp.,A'),Set _Children{C1,C2,…,Cm}(resp.,Set_Children'...,C'n})the set of children-nodes,and Set_Predicate{Q1,Q2,…,Qx}(resp.,Set_Predicate'{Q'1,Q'2,…,Q'y})the set of predicate-nodes.
4)Using the follow ing threemethods to update STs,as the concept-nodes are classified into the three subsets,i.e.,Set_ Parent,Set_Children and Set_Predicate.
(1)A parent-concept-node in Set_Parent:the tree structure of OBN makes each concept-node except the root-node has only one parent-node.Since,only one parent-concept-node is contained in the set Set_Parent.For example,concept-node P is included in the set Set_Parent of A.Next,we can find the sim ilarity Sim(P,P')in the ST of P and use Formula(5)to update Sim(P,P').
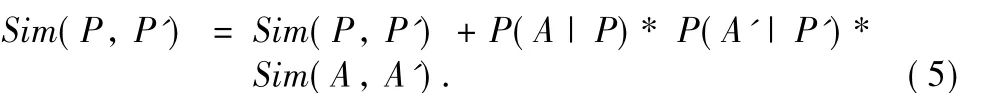
(2)Some children-concept-nodes in Set_Children:a concept-node in OBNmay havemore than one children-conceptnode,and thus we need toupdate each ST of children-conceptnode in Set_Children.For example,children-concept-nodes of C1,C2,…,Cmis included in the Set_Children of A,then we will update the sim ilarity Sim(Ci,C'j)in the ST of conceptnode Ci,where 1≤i≤m,1≤j≤n,and themethod of getting the parameters of Sim(Ci,C'j),is similar to Formula(1).
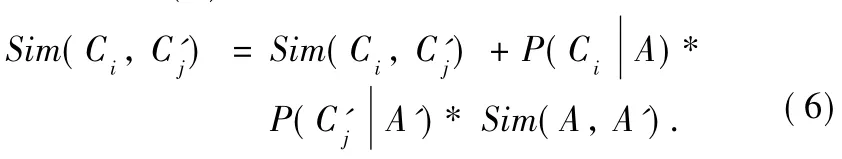
(3)Some predicate-concept-nodes in Set_Predicate:In the set Set_Predicate of a concept-node,there may be multiple predicate-concept-nodes.Therefore the process of updating STs for the predicate-concept-nodes in Set_Predicate is similar to the process described by Formula(2).But no probability exists,which is used to label the predicate-relationship of two conceptnodes.Shown in Fig.5,Qiis one of predicate-concept-nodes of A.We will find that the label between A and Qiis not a similarity but a predicate.When we update Sim(Qi,Q'j)where concept-nodes of Qiand Q'jare the predicate-concept-nodes for themapped concept-nodes of A and A',we need to consider the similarity between two predicates as influence factor.
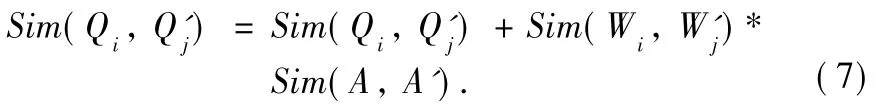
5)Return the firststep and start the next reasoning.During the process aforementioned,the final result is shown in Fig.6. The vertical dashed frames denote the two sets of predicateconcept-nodes,and the horizontal dashed frames represent the two sets of children-concept-nodes.The dotted arrows denote the mapping relationship deduced by the iterative process of mapping-reasoning.
4 Experim ental Results
To evaluate our method OM-BN,we use the set of ontologies(benchmark)provided by the OAEI(Ontology Alignment Evaluation Initiative),which is designed to test the strength and weakness of ontologymappingmethods.In this test set,more than two hundred ontologies are designed.Among them,ontology#101 is considered as the reference ontology,as other ontologies are derived from#101 by modifying its some information,such as names,properties,instances,and so on. In the process of experiment,what we are going to do is to create mappings between#101 and other ontologies by our method OM-BN,respectively.Then,the three parameters,i.e.,precision,recall,and F-Measure are calculated,which are the standard information retrievalmetrics.The definitions of them is shown as follows,where C is the number of correct mappings found by themethod to be tested,F is the number of mappings found by the method,and E is the number of mappings found by ontology experts.
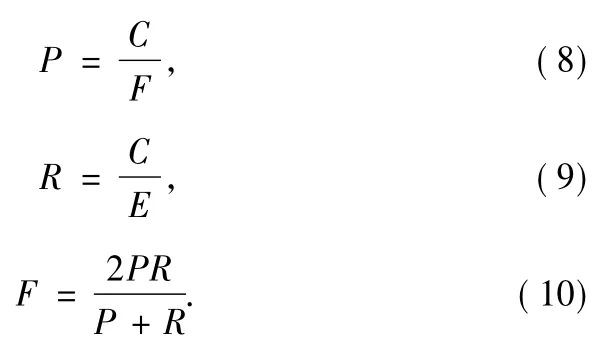
The experimental result for OM-BN is shown in Table 2. We find that the precision,recall and F-Measure are 100%,when OM-BN creates mappings between reference ontology #101 and source ontologies#103 and#104.The reason is that the differences among them are very slight.For instance,the content of#103 and#104 are respectively changed by generalization and restriction of language,compared with #101.In addition,OM-BN has the general performance,when dealing with source ontologies#262,#265,and#266. That is because that the names,comments,and relations in these source ontologies are changed by different conventions,as well as the inexistence of instances and properties. Therefore,OM-BN can only work according to the structural sim ilarity of ontology.The precision,recall and F-Measure are relative low,at around 70%.As for other source ontologies in benchmark,the three parameters are up to 90%.In general,OM-BN performs well,when it is tested by the data in benchmark.
To compare OM-BN with other mapping methods,we evaluate the follow ing methods by precision,recall and FMeasure,each of which is a classic method for ontology mapping,and the experimental results are shown in Fig.7.

Table 2 The results of the benchmark data set

Fig.7 The contrast test formapping methods
5 Conclusions
In this paper,we focus on how to apply BN to ontology mapping,and propose a new method named OM-BN.In OMBN,we first use the characteristics of ontology,i.e.,tree structure and semantic inclusion relation among concepts,and translate ontology into OBN which is simpler than traditional BN.Then we make use of the method of the multi-strategy,which computes sim ilarity more exactly,and create ST for each concept-node in OBN.Finally we use the iterative process of mapping-reasoning to deduce new mappings from the sim ilarities of ST,repeatedly.The iterative process of mapping-reasoning reduces the number of multi-strategies by using the extensional information of ontology,such as structure information and nontaxonomy information in ontology,and thus the sim ilarity calculation ofmulti-strategy is decreased.To sum up,OM-BN is an effective approach for ontology mapping.
[1]Doan A,Madhavan J,Dom ingos P,et al.Learning to Map between Ontologies on the Semantic Web[C].Proceedings of the Eleventh InternationalWorld WideWeb Conference,Hawaii,USA,2002.
[2]Doan A,Madhavan J,Dom ingos P,et al.Learning to Match the Schemas of Data Sources:a Multi-strategy Approach[J]. Machine Learning,2003,50(3):279-301.
[3]Madhavan J,Bernstein P,Rahm E.Generic Schema Matching with Cupid[C].Proceedings of the International Conference on Very Large Databases,Roma,Italy,2001.
[4]Ding Z L,Peng Y,Pan R.A Bayesian Approach to Uncertainty Modeling in OWL Ontology[C].Proceedings of 2004 International Conference on Advances in Intelligent Systems-Theory and Applications,Luxemburg,2004.
[5]Ding Z L,Peng Y.A Probabilistic Extension to Ontology Language OWL[C].Proceedings of the 37th Hawaii International Conference on System Sciences,Hawaii,USA,2004.
[6]M itra P,Noy N F,Jaiswal A R.OMEN:A Probabilistic Ontology Mapping Tool[C].Proceedings International Semantic Web Conference,Banff,Britain,2005.
[7]Pan R,Ding Z L,Yu Y,etal.A Bayesian Network Approach to Ontology Mapping[C].Proceedings International Semantic Web Conference,Galway,Ireland,2005.
[8]Jean-Mary Y,Kabuka M.ASMOV Results for OAEI2007[C]. Proceedings of International Semantic Web Conference 2007 Ontology Matching Workshop,Busan,Korea,2007.
[9]Tang J,Li JZ,Liang B Y,et al.Using Bayesian Decision for Ontology Mapping[J].Journal ofWeb Semantics,2006,4(4): 243-262.
[10]Asooja K,Gracia J.Monolingual and Cross-Lingual Ontology Matching with CIDER-CL:Evaluation Report for OAEI 2013[C].Proceedings of International Semantic Web Conference,Sydney,Australia,2013.
[11]Kuo IH,Wu T T.ODGOMS–Results for OAEI 2013[C]. Proceedings of International Semantic Web Conference,Sydney,Australia,2013.
[12]Fang A,Hong N,Wu S Z,et al.An Integrated Biomedical Ontology Mapping Strategy Based on Multiple Mapping Methods[C].Proceedings of Web Information Systems Engineering-W ISE 2013 Workshops,Berlin Heidelberg,2014.
[13]Do H,Rahm E.Coma:A System for Flexible Combination of Schema Matching Approaches[C].Proceedings of the 28th International Conference on Very Large Data Bases(VLDB),Hong Kong,China,2002.
[14]Giunchiglia F,Shvaiko P,Yatskevich M.S-Match:an Algorithm and Implementation of Semantic Matching[C].Proceedings of the European Semantic Web Symposium,Crete,Greece,2004.
[15]Zhang Z W,Xu D Z,Zhang T.Ontology mapping based on conditional information quantity[C].Proceedings of International Conference on Networking,Sensing and Control,Sanya,China,2008.
[16]Zhang L Y,Yan L,Ma Z M.A Conceptual Graph Based Approach for Mappings among Multiple Fuzzy Ontologies[J]. Journal ofWeb Engineering,2013,12(3/4):215-231.
[17]LüY.An Approach to Ontologies Integration[C].Proceedings of International Conference on Fuzzy Systems and Know ledge Discovery(FSKD),Shanghai,China,2011.
[18]Tatsiopoulos C,Boutsinas B.Ontology Mapping Based on Association Rule M ining[C].Proceedings of 11th International Conference on Enterprise Information Systems,M ilan,Italy,2009.
[19]Tun N N,Dong J S,Tojo S.A Philosophy-Driven Entity Classification and Enrichment for Ontology Mapping[J].Expert Systems,2011,28(2):138-166.
[20]Studer R,Benjam ins V R,Fensel D.Know ledge Engineering: Principles and Methods[J].Data and Know ledge Engineering,1998,25(122):161-197.
[21]Jensen F V.Bayesian Networks and Decision Graphs[M].New York,USA:Springer,2001.
[22]Levenshtein V.Binary Codes Capable of Correcting Deletions,Insertions and Reversals[J].Soviet Physics Doklady,1966,10 (8):707-710.
[23]M itchell T M.Machine Learning[M].New York,USA: McGraw-Hill,1997:154-199.
TG335.58
A
1672-5220(2015)04-0681-07
date:2014-04-20
s:National Natural Science Foundation of China(No.61204127);Natural Science Foundations of Heilongjiang Province,China (Nos.F2015024,F201334);Young Foundation of Qiqihar University,China(No.2014k-M 08)
*Correspondence should be addressed to ZHANG Ling-yu,E-mail:zhanglingyu00217@126.com
杂志排行
Journal of Donghua University(English Edition)的其它文章
- Empirical Analysis of Binary Logistic Model for the Influencing Factors of the Chinese Urban and Rural Residents'Woolen Products Consumption—Based on Questionnaires of 513 Urban and Rural Residents in 16 Provinces
- Analysis of Satisfaction with Business Cost in Shanghai Using Structural Equation Modeling Approach
- Diurnal and Seasonal Variations in Particulate Matter at Shanghai during the Heavy Haze and Non-haze Periods
- Swept-Volume Display System Based on Cylindrical Space Projection and Curved Reflectors
- Existence of Solutions for Infinity-Point Nonlinear Fractional Boundary Value Problem at Resonance
- Human Mouth-State Recognition Based on Image Warping and Sparse Representation Combined with Homotopy
