稳态条件下水平井产能敏感性分析

王　磊，张丽莉，王若东，于建华

（1.中海石油（中国）有限公司蓬勃作业公司，天津300457；2.青海油田公司矿区服务事业部，甘肃敦煌736202；3.长庆油田分公司第七采油厂，甘肃庆阳745100；4.西部钻探吐哈钻井公司，新疆鄯善838200）①

稳态条件下水平井产能敏感性分析

王磊1，张丽莉2，王若东3，于建华4

（1.中海石油（中国）有限公司蓬勃作业公司，天津300457；2.青海油田公司矿区服务事业部，甘肃敦煌736202；3.长庆油田分公司第七采油厂，甘肃庆阳745100；4.西部钻探吐哈钻井公司，新疆鄯善838200）①

在流动参数和储层形状相同的情况下，应用6种不同的裸眼水平井稳态方程，计算了水平井的产能，分析了水平井长度、储层厚度、流量、压降等变量对方程敏感性的影响。结果表明：水平段长度小于304.8 m（1 000 ft）时，所有稳态方程得到的水平井产能计算结果相似；水平段长度大于304.8 m（1 000 ft）时，计算结果出现明显差异且随着水平段长度的增大差异扩大。

水平井；稳态方程；产能比；敏感性

符号说明

a、b—Joshi方程式中的参数，分别代表椭圆供油面积的长轴和短轴，m；

C—Shedid方程常数，m；

Bo—原油地层体积系数（OFVF）；

h—储层厚度，m；

Jh—水平井生产指数，L/（d·Pa－1）；

Kh—渗透率，mD；

L—水平井长度，m；

Jv—直井生产指数，L/（d·Pa－1）；

r—半径，m；

reh—水平井等效供油半径，m；

rev—直井等效供油半径，m；

rw—水平井半径，m；

△p—水平井压降，Pa；

Xe—储层宽度，m；

Ye—平行于水平井轴线的储层高度，m；μo——原油黏度，mPa·s。

在海上油气田开发过程中，由于受环境、气象、海况等因素的影响，海上作业费用高于陆地作业费用，因此，高成本、高风险成为海上石油开发的特点。为使海上石油开发达到预期价值，就必须尽可能采用节约作业时间、降低作业成本、提高最终采收率的新技术新工艺。为了更好地提高水平井的产能，充分发挥出水平井开发的内在潜力，必须进一步研究影响其产能的因素，以提高油藏的采收率。

水平井提高了储层接触面积，从而提高了产量及单井产能。因此，正确地预测水平井产能是必要的。文献调研表明，许多方程可以用来预测稳态条件下的产能［1-7］。因此，油藏工程师必须清楚地了解现有的水平井产能预测方程的敏感性。

如图1所示，水平井可以用割缝衬管、预填砾石衬管、套管外封隔器衬管或固井和射孔衬管进行裸眼完井。本文的敏感性分析仅仅针对没有表皮效应的稳态流动情况下裸眼水平井情况。

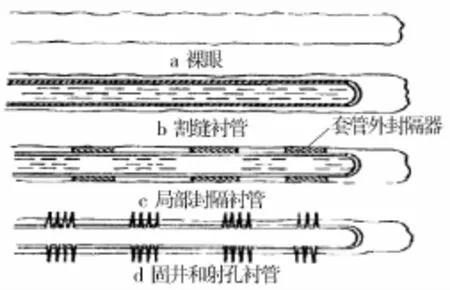
图1　不同水平井完井技术示意

文献中关于沿水平井的压降对井产能的影响存在不同的观点［1-7］。只有当水平井段的压降与储层压降相比可以忽略不计时，描述水平井流动的无限导流井筒假设才成立。事实上要维持井筒中的流动，水平井筒中的压降是必不可少的。因此，沿水平井筒压降问题是油藏工程和采油工程中未解决的问题之一，这也推动了针对沿水平井筒压降对产量影响的研究。

1　裸眼稳态流动方程的评估与对比

目前，已经建立了许多方程来估算水平井的稳态产量。研究人员利用对称的几何形状描述水平供油面积，从而简化求解。根据水平井的几何形状，稳态方程可分为3组，如表1所示［2-7］。第1组是Borisov（1964年）、Joshi（1988年）和Permadi （1993、1995年）假设的椭圆形；第2组是Giger （1983年）、Rengd＆Dupuy（1990年）采用的长方形，两边各有1个半圆（采用对称的几何形状是为了简化求解，并不代表实际的水平供油面积）；第3组是Shedid等人（1996年）建立的变供油截面模型（供油截面为水平井长度的函数），供油面积分为3个部分：①以水平段为中心的长方形（长L，宽2r）；②趾端是半径为r的半圆；③跟部是长为r L/C、宽为2r的小长方形。

表1　水平井裸眼稳态流动方程

1964年，Borisov建立了第1个计算水平井稳态产能的方程，但是没有给出方程的推导过程。因此，并不清楚Borisov方程是怎样得出等效供油半径的，也不清楚方程是如何考虑地层厚度的。1983年，Giger推导出产能方程，论证了替换率，并说明了在相同压降下1口水平井可以代替多少直井。1988年，Joshi推导出斜井和水平井产能方程。1996年，Shedid推导出简化方程，其计算结果与Joshi的方程结果非常接近，但是无需计算等效供油半径reh。这些方程的共同特点都是在没有表皮效应的稳态单相流状态下得到的。

2　产能比Jh/Jv的影响因素分析

为了研究水平井长度和储层厚度对水平井和直井产能比的影响，选择了6种水平井稳态产能方程式，包括Bonsov、Giger、Rengd＆Dupuy、Joshi、Per-madi、Shedid方程，并对这些方程进行了敏感性分析。

1.1 水平井长度对产能比Jh/Jv的影响

以供油面积相同，水平段长度为0～914.4 m（0 ～3 000 ft）的水平井为例，利用上述6个方程研究水平井长度对产能比Jh/Jv的影响。储层厚度不同时，采用不同稳态方程计算产能比Jh/Jv，如图2～5所示。所有结果显示：随着水平段长度增长，产能提高；如果储层厚度增加，产能提高更加明显；薄储层的产能比（Jh/Jv）要比厚储层高。原因在于，相对于产层体积，薄储层中水平井接触面积（或流动面积）要比厚储层中水平井接触面积大得多。

由图2～5可以看出：当水平段长度为304.8 m （1 000 ft），储层厚度为15.24 m（50 ft）时的产能比Jh/Jv几乎是储层厚度为137.16 m（450 ft）时的3倍；随着水平段长度的增长，薄储层的产能比Jh/Jv较厚储层提升明显。因此可以得出结论：所有稳态流动方程证实，水平井适合在薄储层中应用，而不推荐在厚储层中应用。另外，对比结果可以看出：水平井长度不同时，Rcnard＆Du Puy方程得到的Jh/Jv值总是最低；储层厚度不同时，Permadi方程得到的Jh/Jv值总是最高；Bonsov、Joshi和Shedid方程的结果接近。

图2　储层厚度为15.24m（50ft）时采用不同方程得到的水平井长度对Jh/Jv影响的敏感性分析

图3　储层厚度为45.72m（150ft）时采用不同方程得到的水平井长度对Jh/Jv影响的敏感性分析

图4　储层厚度为76.20m（250ft）时采用不同方程得到的水平井长度对Jh/Jv影响的敏感性分析

图5　储层厚度为137.16m（450ft）时采用不同方程得到的水平井长度对Jh/Jv影响的敏感性分析

必须注意：当水平井长度大于822.96 m（2 700 ft）时，不能用Giger方程计算产能。这是因为：水平井长度大于822.96 m（2 700 ft）时，Giger方程分母中的关系式将会因为负值平方根导致结果无穷大。另一方面，由于Shedid方程包含了变量C（即水平井长度的函数），因此仅适用于长度≤914.4 m （3 000 ft）的水平井。

1.2 储层厚度对产能比Jh/Jv的影响

储层厚度为15.24～152.40 m（50～500 ft）、水平井长度为152.4～914.4 m（500～3 000 ft）时，同样使用上述6个方程计算并比较产能比Jh/Jv，如图6～10所示。比较结果进一步证实了先前的结论，即水平井在薄储层中效果更好。储层厚度和水平井长度都不相同时，Permadi方程计算的值最高，Renard＆Duputy方程的值最低；储层厚度和水平井长度相同时，Bonsov、Joshi和Shedid方程的计算结果相似。

图6　水平井长度为152.4m（500ft）时采用不同方程得到的储层厚度对Jh/Jv影响的敏感性分析

图7　水平井长度为304.8m（1000ft）时采用不同方程得到的储层厚度对Jh/Jv影响的敏感性分析

图8　水平井长度为457.2m（1500ft）时采用不同方程得到的储层厚度对Jh/Jv影响的敏感性分析

图9　水平井长度为609.6m（2000ft）时采用不同方程得到的储层厚度对Jh/Jv影响的敏感性分析

图10　水平井长度为914.4m（3000ft）时采用不同方程得到的储层厚度对Jh/Jv影响的敏感性分析

3　压降对水平井产量的影响

同样使用上述6个方程分析水平井产量对压降的敏感性，如图11～15所示。其中，储层厚度为储层厚度为45.72 m（150 ft），压降69～1 380 k Pa（10 ～200 psi），水平井长度30.48～914.40 m（100～3 000 ft）。结果表明：在储层厚度和水平井长度相同的情况下，水平井产能对压降增大十分敏感；井参数和储层条件不变时，Permadi方程计算的产量最高，Renard＆Duputy方程计算的产量最低。因此可以得出结论：水平井中的压降是一个重要因素，可引起水平井产量的变化，因此必须准确测量。

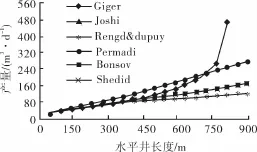
图11　采用不同稳态方程时压降69kPa（10psi）对产量影响的敏感性分析

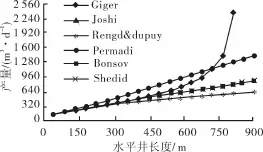
图12　采用不同稳态方程时压降345kPa（50psi）对产量影响的敏感性分析

图13　采用不同稳态方程时压降690kPa（100psi）对产量影响的敏感性分析

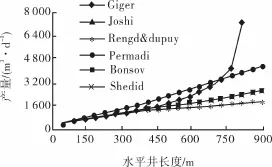
图14　采用不同稳态方程时压降1035kPa（150psi）对产量影响的敏感性分析

图15　采用不同稳态方程时压降1380kPa（200psi）对产量影响的敏感性分析

4　结论

1） 通过对裸眼水平井稳态产能方程的评估、敏感性分析和对比表明：水平段长度小于304.8 m （1 000 ft）时，除了Permadi方程，其余方程得到的产能计算结果都很相似；水平段长度大于304.8 m （1 000 ft）时，各种方程得到的结果出现明显著异，且差异随着水平段长度的增大而扩大。

2） 6个不同稳态流动方程的敏感性分析结果证实，水平井在薄储层中效果比较好，不推荐在厚度h＞76.2 m（250 ft）的厚储层中应用水平井；产能随着水平段长度的增长而提高。

3） 当水平段长度大于822.96 m（2 700 ft）时，不能用Giger方程计算产能；另外，Permadi方程的计算结果比其他方程的结果要高。

4） 裸眼产能方程的对比和敏感性分析表明：储层厚度大于76.2 m（250 ft）时，这些方程的计算结果相似；储层厚度较薄时，计算结果间存在较大差异。

5） 所有稳态流动方程表明：当产层厚度和水平段长度相同时，水平井产能对压降敏感性强，压降对产能有重要的影响。

6） 水平井稳态流动方程的对比表明：当压降、储层厚度、水平段长度相同时，尤其当水平段长度大于304.8 m（1 000 ft）时，Permadi方程得出的产量最高，Renard＆Duputy方程得到的产量最低。

［1］ Lacy S，DingW，Joshi S D.Horizontal Well Applica-tions and Parameters for Economic Success［G］.SPE 23676，1992.

［2］ Joshi S D.Production Forecasting Methods for Hori-zontal Wells［G］.SPE 17580，1988.

［3］ Permadi P.Practical Methods to Forecast Production Performance of Horizontal wells［C］//Kuala Lumpur：the Asia Pacific Oil and Gas Conference，1995-03-20.

［4］ Joshi S D.Augmentation ofWell Productivity with Slant andHorizontal Wells［J］.Joumal of Petroleum Technology，1988（6）：729-739.

［5］ Renard G L，Dupuy J M.Influence of Formation Dam-age on the FlowEfficiency of Horizontal wells［G］.SPE 19414，1990.

［6］ Permadi P.New Formula for Estimating Productivity of Horizontal wells［C］//Annual Indonesian Petrole-um Association Convention，1993-10-03.

［7］ Shedid S A，Osisanyia S，Tiab D.A Simple Productivity Equation for Horizontal Wells Based Upon Drainage Area Concept［G］.SPE 35713，1996.

Sensitivity Analysis of Productivity of Horizontal Wells under Steady-State Conditions

WANG Lei1，ZHANG Lili2，WANG Ruodong3，YU Jianhua4
（1.Pengbo Operating Company，CNOOC（China）Co.，Ltd.，Tianjin 300457，China；2.Mine Area Service Department，Qinghai Oilfield Company，Dunhuang 736202，China；3.No.7 Oil Production Plant，Changqing Oilfield Company，Qingyang 745100，China；4.Tuha Drilling Company，XDEC，Shanshan 838200，China）

In flow parameters and reservoir under the same shape，6 different steady-state equations in openhole horizontal wells were used，horizontal well productivity was calculated and horizontal well length，thickness，and variables such as flow，pressure drop effect on equation of sensitivity were analyzed.Results indicate that length less than 304.8 m（1 000 ft），all steady-state equations of horizontal well productivity results are similar at horizontal length more than 304.8 m（1 000 ft），the result appears obvious differences and differences with increasing length.

horizontal well；steady-state equations of capacity；sensitivity

TE934

B

10.3969/j.issn.1001-3482.2015.07.019

1001-3482（2015）07-0078-05

①2015-01-30

王 磊（1988-），男，陕西渭南人，主要从事海上油气生产管理工作，E-mail：wanglei118＠cnooc.com.cn。