水下采油树生产通道可靠性设计及分析

罗建梅，谢　哲，段礼祥，段梦兰

（1.中国石油大学（北京）a.海洋油气研究中心；b.机械与储运工程学院，北京102249；2.中海油安全环保分公司，天津300456）①

设计计算

水下采油树生产通道可靠性设计及分析

罗建梅1a，b，谢哲2，段礼祥1b，段梦兰1a，b

（1.中国石油大学（北京）a.海洋油气研究中心；b.机械与储运工程学院，北京102249；2.中海油安全环保分公司，天津300456）①

水下采油树所处海底环境较为复杂，需要对水下采油树的各重要部件进行高可靠性设计。针对水深1 500 m、压力等级69 MPa的设计条件，根据ASME B31.3中高压管道壁厚公式计算出水下采油树生产管道壁厚为11 mm。在安全系数设计的基础上，综合了有限元分析、蒙特卡洛模拟方法，对生产管道进行可靠性分析，验证了设计壁厚的可靠性满足强度要求，并根据灵敏度分析得出影响生产管道可靠度的关键因素是壁厚、内压和材料屈服极限。

采油树生产管道；安全系数；蒙特卡洛模拟；可靠性

随着国际能源形势的发展，石油开采走向海洋、走向深水的趋势越来越明显。水下生产系统是水下油气生产的常用开发模式，水下采油树是水下生产系统的关键设备，是油气从地层到管路的生产控制装置。水下采油树树体结构和管路系统等需满足较高的可靠性指标。目前，国内外深水项目一般要求水下生产系统的可靠性大于95%。例如：AKPO油田要求可靠度达98.35%；我国南海某气田要求水下生产系统可靠性为98%［1］；挪威的Ingrid Almas Berg［2］指出海洋石油中的水下工艺系统的可靠性一般要求为97%；Dong hun Lee［3］指出水下生产系统设计应达到99%的可靠性。所以在研发阶段，如何通过可靠性设计提高其固有可靠性成为关键性问题。传统的机械结构设计是以安全系数作为准则，安全系数法是一个重要的传统结构设计方法，它将设计值与实际值之间可能存在的差量，通过一个大于1的系数来反映，以保证结构设计值的可靠性。该方法简单快捷，虽然预留了一定的安全裕量，但设计过程中没有考虑工程材料、尺寸以及载荷等参数的随机性，不能确切保证产品的可靠性水平，也不利于产品的优化改进［4］。

为确保水下采油树的高可靠性设计水平，本文在传统安全系数法设计基础上，对设计参数随机性进行了研究，并结合ANSYS有限元分析和蒙特卡洛（Monte-Carlo）模拟技术，提出了基于安全系数的生产管道可靠性设计模型，能够有效地解决2种方法独立应用的缺陷。

1　基于安全系数的壁厚设计

水下采油树生产管道是油气从采油树主体经过阀门后到跨接管的过流通道，是1段不对称U形管，如图1所示。管道内部主要受流体压力、冲蚀和腐蚀，是设计壁厚和选材时考虑的主要因素。

图1　水下采油树

根据经验，管材选择耐腐蚀性较好的8630钢。生产管道的结构参数包括壁厚参数、形状参数等，在此仅列出壁厚等参数的设计方法，根据标准ASME B31.3中高压管道按内径确定壁厚公式计算。依据生产侧阀组的尺寸103.2 mm（4英寸），确定生产管道的内径为103 mm，根据标准ASME B31.3公式得

式中：t为管道计算壁厚；p为设计内压；d为管道内径；S为材料许用应力；c1为腐蚀裕量。

依据设计条件，设计压力p＝69 MPa；d＝103 mm；8630钢平均屈服极限Y＝805 MPa，则许用应力为

式中：Y为材料屈服极限；k为材料均匀系数（取k＝1）；m为工作条件参数（取m＝0.95）；n为过载系数，即安全系数（取n＝1.5）。

材料的腐蚀裕量根据介质对材料的均匀腐蚀率与容器的设计寿命决定，即

式中：K为腐蚀速率，mm/a；B为容器的设计寿命。

设计寿命为20 a，当介质为油气时，取极限腐蚀裕量c1＝4 mm。

则由式（1）～（3）可得其设计壁厚为

2　生产通道的可靠性分析

2.1 可靠性理论

管道的可靠性主要是管道结构的可靠性，结构可靠性的基本定义是：结构在规定的时间内、规定的条件下完成规定功能的能力。可靠度则是可靠性的概率度量，其定义为：在规定的时间内、规定的条件下完成规定功能的概率［5］。在结构的施工和使用过程中，结构是以安全和失效2种状态存在的，为正确地描述结构所处的状态，需要列出极限状态函数，建立可靠性模型。设X1，X2，…，Xn为影响结构状态的n个随机变量，则状态函数Z可写成

通常称式（5）这个随机变量的函数为极限状态函数。Z＞0时，结构处于可靠状态；Z＜0时，结构处于失效状态；Z＝0时，结构处于临界状态或称为极限状态。

管道结构可靠度模型中，设Sh（Strength）为结构强度，Ss（Stress）为应力，则结构的功能函数可定义为：Z＝Sh－Ss；则失效概率的计算公式为：P（Z＜0）。图2为在直角坐标系中表示了应力S和强度R的概率函数曲线，图中应力小于强度的重叠部分，即意味着管道结构失效，称为干涉区。根据干涉情况进行管道可靠性计算的理论称为应力-强度干涉理论，这种模型，也称为干涉模型［6］。通过该模型确定管道的可靠度，通常有分析和模拟2种方法。模拟方法由于简单易行，且对历史数据依赖较少被广泛运用，本文应用基于Monte-Carlo的模拟对生产管道的可靠性进行分析。

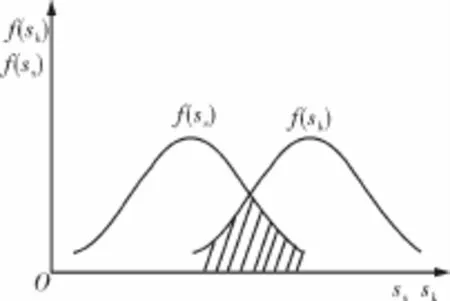
图2　应力强度干涉模型

2.2 基于Monte-carlo可靠性分析

Monte-carlo是对随机变量的大批抽样，通过结构失效频率来计算结构的失效概率，也是被公认相对精确的一种结构可靠度分析方法。ANSYS中的概率设计（PDS）功能实现了蒙特卡洛模拟和有限元的结合，它可以考虑输入参数的不确定性，得出结果的置信区间，以及参数的灵敏性影响参数间的相关系数等。下面对采油树生产管道进行可靠性模拟分析。

1） 按照相关参数建立生产管道分析模型，进行网格划分（如图3所示），并加载分析得到应力云图，如图4所示。

根据计算结果，提取最大应力σmax，建立极限状态方程，即

式中：Y为材料屈服极限；σmax为静力学分析最大应力。

图3　生产管道模型的有限元网格划分

图4　应力分析云图

2） 保存静力学分析文件，导入PDS模块，输入变量。

影响生产管道可靠性的影响因素众多，在此就其主要因素进行分析。首先，内压是油气管道承受的主要载荷，由于油气产量一般考虑为正态分布，所以管道所承受的内压也考虑为正态分布，且管道的操作压力具有明显的变异性，而管线的尺寸主要是内外径，其本身的变异系数很小［7］。管道材料的屈服强度、抗拉强度极限、管材的弹性模量的概率分布一般也考虑为正态分布［8］。生产管道的分析参数设置如表1所示。结构的几何尺寸如长度、内外径和壁厚等参数由于测量和加工误差的影响，最终制造件的尺寸具有一定的随机性，服从一定的分布规律。一般来说，实践证明零部件的尺寸误差符合一定范围内的正态分布［910］。

则变异系数为

变异系数表示随机变量的相对分散程度，是一个无量纲量，对于工程应用来说，常用的变异系数取0.03～0.10［11］。

表1　模型中输入参数的随机特征

3） 结果分析。

弹性模量的均值抽样结果如图5所示，可以看出：模拟计算结果与给定的正态分布类型相符，因此2000次模拟能满足模拟次数要求。图6～8分别是状态函数Z值的抽样历程图、抽样分布直方图和累积概率分布图。

图5　弹性模量均值抽样分布

图6　Z值的抽样历程

图7　Z值的分布直方图

由图8可以看出：功能函数Z值最小值Zmin＝216.09 MPa，所以Z＞0的概率为100%，即其结构可靠度为100%。基于安全系数的壁厚设计符合水下采油树生产管道的可靠性要求。

影响功能函数Z值的输入随机变量的敏感度如图9所示，结果表明：影响其可靠性的重要因素为管道屈服极限Y、管道内压p1及壁厚t等。因此在管道的可靠性设计中，应首先考虑管道的内外径设计和管道内部载荷。随机参数对生产管道结构可靠度的敏感程度可以在结构设计时予以重点考虑，从影响其可靠性的关键因素着手显著提高其可靠性。

图8　Z值的累积失效概率分布

图9　随机参数的敏感度

3　结论

1） 针对水深1500m、压力69MPa的设计条件，根据ASME B31.3中高压管道按内径确定壁厚公式，设计的采油树生产管道壁厚11mm。

2） 通过分析可知，该生产管道的结构可靠度为100%，而且有较大的强度裕量，所以此设计满足水下采油树部件的高可靠性要求，验证了基于安全系数设计管道壁厚的可靠性。

3） 通过参数敏感性分析可知，影响生产管道可靠度的关键因素是壁厚、内压和屈服极限，在设计时应予以重点考虑，并且保证其较高的精度。

4） 影响生产管道可靠性的因素很多，但并非都服从正态分布，可靠性分析时影响参数的分布类型应通过特定工况下的统计结果确定，使分析更加准确。

［1］ 尹丰.南海某气田水下生产系统可靠性保障设计［J］.石油矿场机械，2012，41（7）：23-25.

［2］ Berg I A A S.Design for Reliability--Applied to devel-opment of subsea process systems［D］.Trondheim：Norwegian University of Science and Technology De-partment of Production and Quality Engineering，2010.

［3］ Lee D，Nam K，Kim J，et al.RAM study on the subsea production system of an offshore oil and gas platform ［C］//The Fourteenth International Offshore and Polar Engineering Conference.International Society of Off-shore and Polar Engineers，2004.

［4］ 帅健.油气管道可靠性的极限状态设计方法［J］.石油规划设计，2002，13（1）：18-21.

［5］ 赵国藩，金良伟，贡金鑫.机构可靠度理论［M］.北京：中国建筑工业出版社，2000.

［6］ 吴世伟.结构可靠性分析［M］.北京：人民交通出版社，1990.

［7］ Ahammed M，Melchers R.Probabilistic analysis of un-derground pipelines subject to combined stress and cor-rosion［J］.EngineeringStructures，1997，19（12）：988-994.

［8］ 牟致忠，朱文予.机械可靠性设计［M］.北京：机械工业出版社，1993.

［9］ Elsayed E A.Reliability engineering［M］.America：Wi-ley publishing，2012.

［10］ 张建国，苏多，刘英卫.机械产品可靠性分析与优化［M］.北京：电子工业出版社，2008.

［11］ 麻栋兰.大型离心压缩机叶轮可靠性研究［D］.大连：大连理工大学，2009.

Reliability design and Analysis of Subsea Production Flowloop

LUO Jianmei1a，b，XIE Zhe2，DUANLixiang1b，DUANMenglan1a，b
（1.a.Offshore Oil and Gas Research Center；b.College of Mechanical and Transportation Engineering，China University of Petroleum，Beijing 102249，China；2.CNOOC Safety Technology&Services Company，Tianjin 300456，China）

Subsea tree at the bottom of the sea which environment is relatively complex，it is neces-sary to make the reliability design research on important components.Under the design conditions of water depth being 1 500 m and pressure grade being 69 MPa，the thickness of production flow-loop is designed as 11mm，according to the standard of ASME B31.3.Synthesis the finite element analysis and Monte-carlo simulation method，the reliability analysis is carried out on the produc-tion flowloop and validated reliability of the thickness met the strength requirement.The result of sensitivity analysis shows that the influent factor of production flowloop reliability is thickness，inter pressure and yield limit.

subsea tree production flowloop；safety coefficient；Monte-carlo simulation；reliability

TE952

A

10.3969/j.issn.1001-3482.2015.07.007

1001-3482（2015）07-0028-05

①2015-01-01

国家发展改革委2013海洋工程装备研发及产业化专项“水下采油树研发及产业化”（F13QW）

罗建梅（1989-），女，河北邯郸人，硕士研究生，主要从事海洋石油装备及作业安全技术与理论研究，Email：luo-jianmei110＠163.com。