管土接触作用下埋地管道力学分析

杨　辉，王　婷，雷铮强，李明菲，玄文博，王富祥，陈　健

（中国石油管道科技研究中心，河北廊坊065000）①

管土接触作用下埋地管道力学分析

杨辉，王婷，雷铮强，李明菲，玄文博，王富祥，陈健

（中国石油管道科技研究中心，河北廊坊065000）①

为了研究管土间作用规律，运用ANSYS软件建立了基于接触单元的三维管土接触有限元模型，分析得到了管周接触应力的分布。给出了管土相互作用计算的弹性解，对比分析得出其与有限元模拟结果非常接近，表明管土接触分析模型能够较好地模拟管土相互作用。计算分析了管道埋深、土体粘聚力、管土摩擦因数、内摩擦角对管土接触应力的影响。

管土接触；埋地管道；ANSYS；力学分析

目前，我国70%的石油和99%的天然气通过管道运输，而绝大部分管道为埋地管道［1］。管周土体既对管道施以载荷，又约束管壁向外变形，管-土间的相互作用非常复杂，研究管-土作用规律对埋地管道应力分析具有重要意义［2］。20世纪70年代，Winker提出了弹性地基梁的概念，后来被引入到管土相互作用的研究中。张坤勇等［3］在Winkler经典解答基础上，给出了一种适用于描述任意位移荷载条件下管线的解析解。王小龙等［4］基于Winkler假设的弹性地基梁理论，建立了埋地钢管在局部悬空时管道与土相互作用的力学模型。上述弹性地基梁模型是通过若干弹簧将管道与土连接起来分析管道与土介质的相互作用，模型存在大量简化，且不能较好地模拟管土间的非线性摩擦。本文运用ANSYS软件，基于接触单元建立了三维管土接触有限元模型，分析了管道埋深、土体粘聚力、管土摩擦因数、内摩擦角对管土接触应力的影响。

1　管土接触有限元模型

1.1 材料模型

管材选用X70管线钢，其本构采用Ramberg-Osgood模型，其表达式为［5-6］

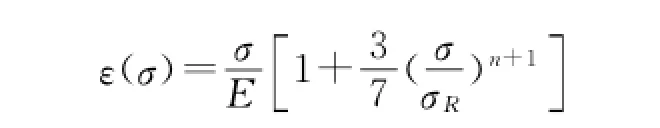
其中：

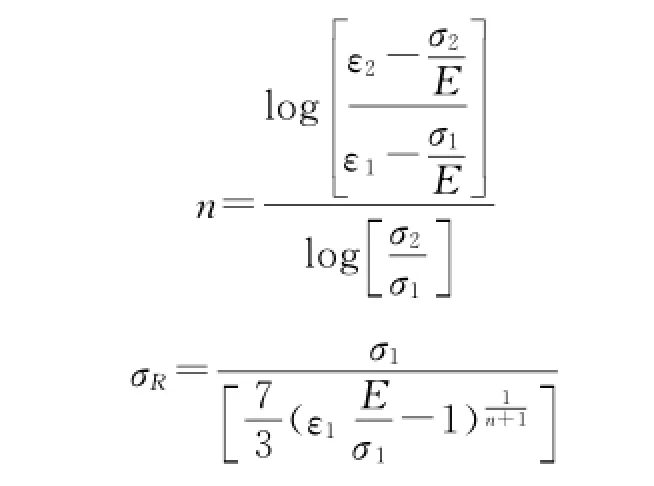
式中：ε（σ）为管材总应变；σ为管材总应力，MPa；E为管材弹性模量，GPa；σR为Ramberg-Osgood应力，MPa；n为管材的硬化系数；取X70管线钢相对应的参数σ1＝σy＝480MPa，ε1＝0.005，σ2＝σu＝570 MPa，ε2＝0.2。

土体本构采用Drucker-Prager模型，其表达式为［7-8］

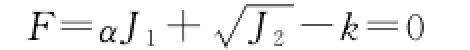
其中：

式中：F为屈服函数；J1为应力张量第一不变量；J2为应力偏量第二不变量；σ1、σ2、σ3分别为第一主应力、第二主应力和第三主应力，MPa；α和k为正的材料常数；c为土体粘聚力，kPa；为内摩擦角，（°）。

管道与土体的材料参数如表1所示。

表1　管道与土体材料参数

1.2 单元选择

管道和土体单元均选择SOLID95，为3D20节点结构实体单元，具有塑性、蠕变、膨胀、应力刚化、大变形、大应变等特性。由于采用协调的位移函数，SOLID95可以很好地适应曲线边界。

管道与土体间采用面-面接触方式，接触单元选择CONTA174，目标单元选择TARGE170。CON-TA174为3D8节点面面接触单元，可描述3D目标面（TARGE170单元）同该单元所定义的变形面间的接触和滑移状态，支持库仑和剪应力摩擦。TARGE170为3D目标单元，通过共享实常数号与接触单元构成接触对，可方便地模拟复杂的目标形状［8-10］。

1.3 网格划分与边界加载

模型相关尺寸参数如下：管径D＝0.813 m，壁厚t＝0.014 m，土体宽度W＝7D，高度H＝7D，长度L＝10 m。管道和土体均采用六面体网格划分，如图1a所示。由于土体刚度明显较管道小，因此选择管道外壁为目标面，对应的土体表面为接触面，并分布在2个表面上创建目标单元与接触单元，构成接触对，如图1b所示。

模型底面为固定约束，上表面为自由面，四周剖面约束垂直方向，施加重力载荷。

图1　划分网格与创建接触对

2　管土相互作用的弹性解答

运用弹性力学理论［11］，将埋地管道管周土压力问题转化为重力场下半无限二维弹性介质内圆环孔边应力集中问题进行求解，如图2所示。

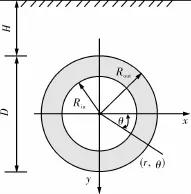
图2　管土相互作用的弹性力学模型

考虑管土间的变形协调条件，通过应力函数求解得到管周应力的弹性解。

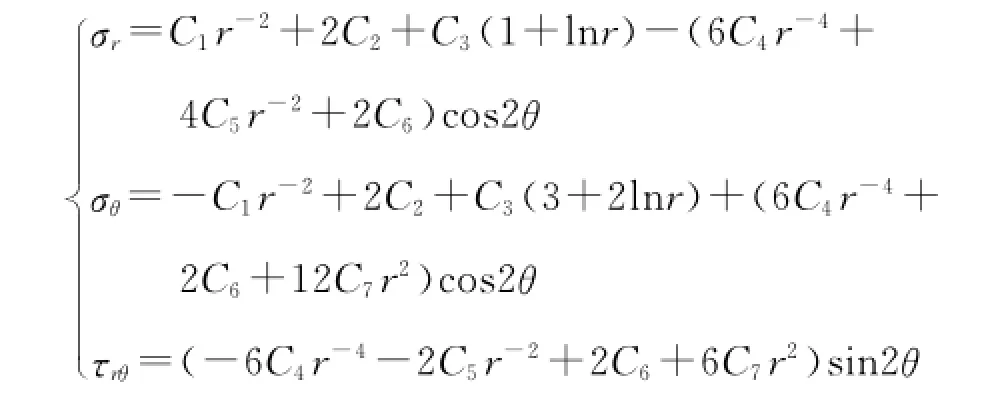
其中：

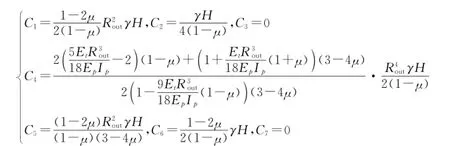
式中：σr、σθ、τrθ分别为土体径向正应力、环向正应力和剪应力，Pa；r、θ分别为径向和环向坐标；μ为土体泊松比；Rout为管道外半径，m；γ为覆土容重，N/m3；H为覆土厚度，m；Et为土体变形模量，Pa；Ep为管道弹性模量，Pa；Ip＝δ3/12，为管壁截面惯性矩；δ为管道壁厚，m。

分别采用有限元方法与弹性力学理论计算得到径向压应力与剪应力沿管壁周向分布，如图3～4所示。由图3～4可见：管周接触应力按照近似正弦规律变化，有限元解与弹性解析解较为接近，验证了管土接触有限元模型的可用性；最大径向压应力位于管顶与管底；由于在有限元分析中考虑了管道重力，因此管底径向压应力稍大于管顶径向压应力；管壁两侧径向压应力最小，说明管壁两侧管土相互作用不明显；管壁剪应力关于x轴近似对称分布，最大值位于管壁45°、135°、225°和315°处，最小值位于管顶、管底及两侧，接近于零。

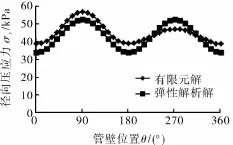
图3　径向压应力随管壁周向分布

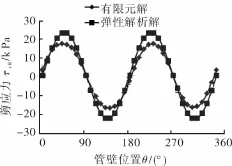
图4　剪应力随管壁周向分布

3　算例分析

针对不同工况（如表2）对埋地管道进行力学分析，分别得出管周最大径向压应力与最大剪应力随埋深、土体粘聚力、摩擦因数与内摩擦角的变化规律，如图5～8所示。

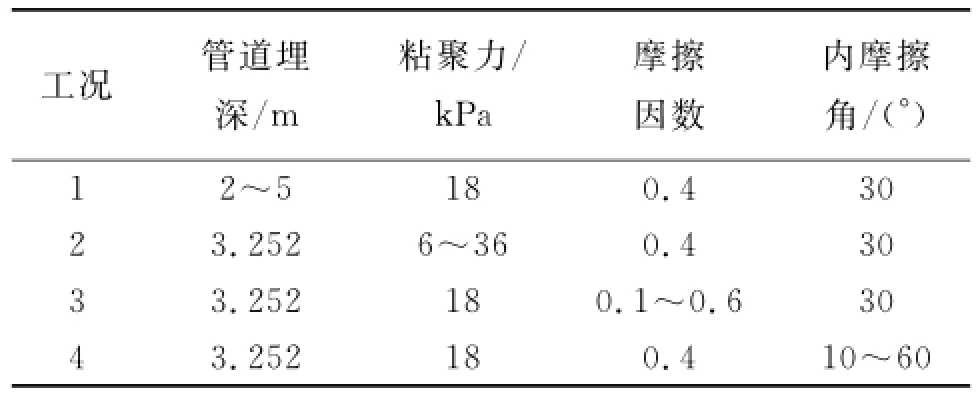
表2　不同工况埋地管道力学分析

由图5可以看出：最大径向压应力与最大剪应力随管道埋深增加呈近似线性递增，且径向压应力增幅更为明显。由图6和图8看出：土体粘聚力与内摩擦角对管周接触应力的影响很小，最大径向压应力与最大剪应力随粘聚力与内摩擦角的变化几乎保持不变。由图7可以看出：最大径向压应力随着管土摩擦因数增大而逐渐减小，而最大剪应力随着管土摩擦因数增大而逐渐增大；当摩擦因数大于等于0.5时，接触应力变化幅度很小，说明管土摩擦因数大于等于0.5后其对管土接触应力的影响不大。

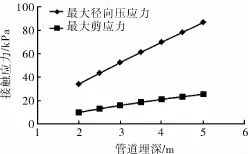
图5　管道埋深对管土接触应力的影响

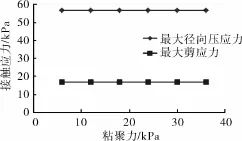
图6　土体粘聚力对管土接触应力的影响

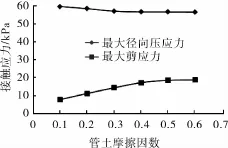
图7　管土摩擦因数对管土接触应力的影响

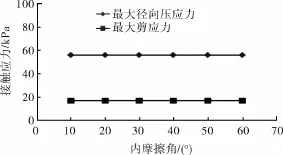
图8　土体内摩擦角对管土接触应力的影响

4　结论

1） 运用ANSYS软件建立了基于接触单元的三维管土接触有限元模型，分析得到了管周接触应力的分布。通过对比管土相互作用计算的弹性解得出，管周接触应力按照近似正弦规律变化，有限元解与弹性解析解较为接近。

2） 最大径向压应力位于管顶与管底，管壁两侧径向压应力最小，说明管壁两侧管土相互作用不明显。管壁剪应力关于x轴近似对称分布，最大值位于管壁45°、135°、225°和315°处，最小值位于管顶、管底及两侧，接近于零。

3） 最大径向压应力与最大剪应力随管道埋深增大呈近似线性增加，随土体粘聚力与内摩擦角增大几乎保持不变；最大径向压应力随着管土摩擦因数增大而逐渐减小，而最大剪应力随着管土摩擦因数增大而逐渐增大。当摩擦因数大于等于0.5时，接触应力变化幅度很小，说明管土摩擦因数大于0.5时其对管土接触应力的影响不大。

［1］ 佘艳华.机械冲击荷载对邻近埋地管道的影响及控制研究［D］.绵阳：中国工程物理研究院，2012.

［2］ 郝婷，陈贵清.管道与土的相互作用［J］.水利科技与经济，2007，13（4）：237-239.

［3］ 张坤勇，王宇，艾英钵.任意荷载下管土相互作用解答［J］.岩土工程学报，2010，32（8）：1189-1193.

［4］ 王小龙，姚安林.埋地钢管局部悬空的挠度和内力分析［J］.工程力学，2008，25（8）：218-222.

［5］ 杨辉，汤怡，陈健，等.油气管道体积型腐蚀缺陷有限元仿真［J］.油气储运，2015，34（1）：37-41.

［6］ 王阿敏.单点腐蚀管道在内压作用下的极限承载力［D］.大连：大连理工大学，2012.

［7］ 王联伟，张雷，董绍华，等.管土接触作用下管道沉陷复杂应力分析［J］.油气储运，2013，32（11）：1179-1182.

［8］ ANSYS Inc.ANSYS mechanical APDL and mechanical applications theory reference［M］.Canonsburg PA：ANSYS Inc.，2010：69-98.

［9］ 王新敏，李义强，许宏伟.ANSYS结构分析单元与应用［M］.北京：人民交通出版社，2011.

［10］ 赵吉，姜民政，李青红.埋地输油管道在线大修应力应变分析［J］.石油矿场机械，2004，33（1）：77-78.

［11］ 徐芝纶.弹性力学［M］.北京：高等教育出版社，2006.

Analysis on Mechanical Characteristics of Buried Pipeline under Pipe-Soil Contact

YANG Hui，WANG Ting，LEI Zhengqiang，LI Mingfei，XUANWenbo，WANG Fuxiang，CHEN Jian
（PetroChina Pipeline R&D Center，Langfang 065000，China）

For studying the law of pipe-soil interaction，modeling 3D pipe-soil contact finite-element analysis based on contact elements using ANSYS，the distribution of pipe circumferential contact stress is analyzed.The elastic solution of pipe-soil interaction is provided，which is close to the fi-nite element solution，showing that the pipe-soil contact model can simulate pipe-soil interaction well.Finally，effects of pipe circumferential contact stresses of different parameters are analyzed，including buried depth，soil cohesive force，friction factor and internal friction angle.

pipe-soil contact；buried pipeline；ANSYS；mechanical characteristics

TE931.2

A

10.3969/j.issn.1001-3482.2015.07.011

1001-3482（2015）07-0044-04

①2015-01-19

中国石油管道公司科技攻关项目“管道环焊缝缺陷漏磁检测信号识别与评价技术研究”（20130204）

杨 辉（1987-），男，湖北荆州人，硕士，主要从事管道完整性内检测与评价工作，E-mail：yanghui07＠petrochina.com.cn。