基于ABAQUS的钻井平台锁紧系统有限元分析

王建才，杨立东，田 俊，马树宇

基于ABAQUS的钻井平台锁紧系统有限元分析

王建才1，杨立东2，田 俊1，马树宇1

（1．渤海装备辽河重工有限公司，辽宁盘锦124010；2．盘锦凯瑞能源有限公司，辽宁盘锦124010）①

锁紧系统是自升式钻井平台的关键部件，其可靠性对于平台自身安全至关重要。利用传统的力学公式和计算方法很难验算锁紧系统各部件应力的大小及分布。为验证锁紧系统结构的合理性，以有限元软件ABAQUS将锁紧系统各部件划分为规则的六面体网格单元，并以非线性模块作为计算分析平台对其进行强度分析，根据计算结果进行强度校核。结果表明，锁紧系统各部件均能满足强度要求，同时也为开发锁紧系统相关系列产品提供了可靠数据。

钻井平台；锁紧系统；非线性；强度校核

自升式钻井平台是近年来近海油气勘探开发中使用最广泛的海洋工程装备之一，平台锁紧系统是自升式钻井平台的关键核心部件。对于锁紧装置而言，安全可靠性设计是极其重要的环节，研制性能良好的锁紧装置对于平台的安全稳定起关键作用。因此，需要设计出合理的结构，选取合适的零部件材料，采取适宜的计算方法，来验证锁紧系统在实际作业工况中能否达到使用要求。

1　结构组成

同以前的锁紧机构相比，新研制的锁紧系统无论在结构和承载能力上都有了较大的提升和改进。锁紧系统的整体钢架采用拼接式结构，内部零件采取锻、铸结合的工艺，不但结构简单，而且焊接组装等工序较为方便，降低了装配后的成本和风险，也使得设计人员在研发初期就能对锁紧系统的整体性有进一步的理性认识［1］。新研制的锁紧系统结构如图1所示。

图1　锁紧系统结构

2　锁紧系统有限元分析理论

六面体单元是拥有局部和整体两个坐标系的三维单元，可用线性函数描述［2-3］。其基本参数如应力、应变等与弹性模量E和泊松比μ有关联，每个六面体单元有8个节点且每个节点有3个自由度。分析计算的基本步骤如下。

2．1 结构离散化

将整体离散成有限个微分体dxdydz，任取一个来探讨应力应变之间的关系。整体在外部载荷的作用下，体内任一点的应力状态由6个应力分σx、σy、σz、τxy、τyz、τzx来表示。其中，σx、σy、σz表示各坐标轴上的正应力，τxy、τyz、τzx表示各平面内的剪应力，微观模型如图2所示。

图2　微六面体单元的力学模型

2．2 单元分析

由弹性力学可知，弹性体内任取一点处的应力、应变和位移间的关系可根据以下公式描述出：

1） 位移和应变间的关系。

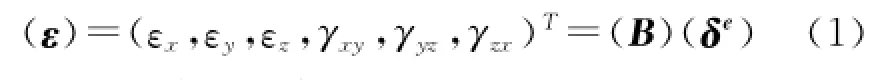
式中：（ε）为单元内任一点处的应变矩阵；εx、εy、εz为任一点处的正应变；γxy、γyz、γzx为任一点处的剪应变；（B）为几何矩阵；（δe）为单元节点位移矩阵。

2） 应变和应力间的关系。

式中：（σ）为单元内任一点处的应力矩阵；（D）为弹性矩阵；E为单元所属材料的弹性模量；μ为单元所属材料的泊松比。

3） 单元刚度方程。

根据虚功原理建立单元刚度方程，单元节点力和节点位移间的关系即可在方程中显现出来。

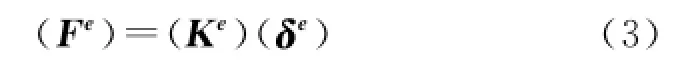
式中：（Fe）为单元节点载荷矩阵；（Ke）为单元刚度矩阵。

2．3 整体分析

在单个单元刚度方程的基础上，通过集成得到整体刚度方程，在此基础上进行整体结构分析。集成的原则是相邻单元间在共用节点处的位移也相同。

式中：（F）为整体节点载荷矩阵；（K）为整体刚度矩阵；（δ）为整体节点位移矩阵。

2．4 求解节点位移及单元的应变与应力

求解方程式（4）。根据得出的节点位移，代入式（1）～（2）并计算，即可得到相应单元节点的应变和应力。

3　锁紧系统的有限元模型建立

有限元软件自身的建模功能与专业的三维绘图软件对比而言，其功能相对单一，但均与各绘图软件有着良好的接口程序，因此锁紧系统实体模型采用U G进行建模，之后导入ABAQUS软件中将模型进行规则的六面体网格划分，以提高分析计算结果的精度。确保模型在分析计算过程中能够达到所需精度的前提下，将实体结构中的部分细小倒角，螺栓孔等对整体强度影响较小的结构进行简化处理，以缩短不必要的计算时间［4］。以ABAQUS软件的非线性分析模块作为分析平台，对锁紧系统加载极限载荷的工况下进行极限强度分析，并对计算结果进行必要的后处理。

在对锁紧系统进行强度分析的同时，将其内部结构如锁紧齿条、压块等锁紧装置中的关键部件进行建模，尽量做到与实际情况相一致，从而减少因外部条件改变造成的计算误差。因此在分析过程中采取的分析类型为边界非线性。此类问题在物体相互接触边界位置以及接触面上的应力大小和分布事先是未知的，将整个问题求解完成后才能确定各接触面的受力情况以及位移变化。

前处理在整个有限元分析过程中所花费的时间和精力是最多的，占整个过程的70%左右。而前处理过程中，有限元模型网格质量对于求解的精度和准确度有着决定性的影响。前处理的效率高低以及质量好坏对整个有限元分析重要性很高。在接触分析中，同等条件下，六面体网格要比四面体网格仿真的结果更为准确，在接触起作用的同时也能使分析更容易收敛，这也是本次锁紧系统采用六面体单元为主分析的原因。

锁紧系统实体模型选用8节点六面体单元对其进行规则的网格划分，压块加载端面采用主控制点与MPC刚性梁单元结合的形式进行连接，以模仿极端载荷的加载形式。桩腿齿条施加对称的固定约束方式，锁紧系统内部各接触件如导轨架与压块，压块与锁紧齿条，锁紧齿条与桩腿件均建立接触对，以模仿实际情况下两两物体的接触状态。

因锁紧装置为左右对称结构，因此在有限元建模过程中只建立1／2结构，这样不但节省建模周期，也能简化计算过程，节省前处理的时间。有限元模型如图3所示。

图3　锁紧系统有限元模型

本次分析选取极限载荷工况进行应力分析，极端载荷为7．2×104k N。因为模型成对称性模型，所以计算采用半模型进行分析计算，对称面上施加对称边界约束，加载取3．6×104k N进行分析计算。

锁紧齿条和楔块的材质均为40CrNiMo，其综合力学性能良好，有高的强度、韧度和良好的淬透性和抗过热的稳定性，使其广泛用于制造强度高、塑性好的重要零部件。桩腿齿条采用A517Q，导轨架材料选为E550，其基本属性如表1。

表1　材料基本属性

本次有限元分析，在对模型附着材料属性时的单位制是mmNMPa，其原因是有限元软件中没有固定的单位制，因此在对模型附着材料属性时，其数值本身所含有的特定单位将被软件作为默认值［5］。

4　锁紧装置的强度分析

有限元位移法的分析方程可归纳为：

式中：K为结构刚度矩阵；U为位移列向量；F为外载荷列向量。

在分析过程中用到了多点约束即MPC。MPC通过多点约束的形式将不同的节点进行耦合连接，MPC内部合力为零，其不会增加结构的刚度，并且运用梁单元将各不同部件连接，其计算过程仍可看作是线性的，此举节省了大量的前后处理时间。MPC单元即多点约束刚性梁有如下特性：

式中：ui为节点i处的平动矢量；ei为节点i处的转动矢量；φ为当前坐标系下的旋转角。

由式（6）可得到3个附加方程来处理实体单元与梁单元间不同自由度数之间耦合的问题［6］。

根据材料力学方面的理论可知，在一定厚度的范围内，板材厚度对材料的许用应力是没有影响的。但随着板材厚度的增加以及制造工艺的改变可能使板材内部存在缺陷等，就会造成材料的力学性能随着板材厚度的增加而下降现象的普遍发生。为此，在锁紧系统的设计过程中，这方面的因素也在考虑范围之内，从而加强了设计的合理性和可行性［7-8］。根据《海上移动平台入级规范》，取材料的一般局部安全系数γm＝1．1。锁紧系统关键部件锁紧齿条、楔块、导轨架的有限元分析应力云图分别如图4～6所示。

图4　锁紧齿条应力云图

图5　楔块应力云图

根据图4锁紧齿条应力云图所示，在非线性计算分析中，由于楔块与锁紧齿条应力接触造成锁紧齿条后端棱角出现应力集中问题，对零件真实使用效果无直接影响，所以锁紧齿条最大的合理计算应力值可取为720mPa，材料许用应力为800mPa，安全系数为1．11，符合规范要求。

根据图5楔块应力云图所示，楔块由于边界条件中MPC的存在，造成了附近应力集中问题，对零件的真实使用效果无失效影响，楔块的合理计算应力为720mPa，材料许用应力为800mPa，安全系数为1．11，符合规范要求。

图6　导轨架应力云图

根据图6导轨架应力云图所示，导轨架模型中存在90°尖角的缘故，造成了其附近应力集中现象的存在，此现象的存在对零件的真实使用效果无失效影响，导轨架计算应力为495mPa，材料许用应力为550mPa，安全系数为1．11，符合规范要求。

5　结论

1） 本锁紧系统达到了结构强度要求，并通过了船级社的相关认证，实现了预期的设计目的，同时为相关零部件的研发设计提供了真实可信的参考数据。

2） 锁紧系统在施加极限载荷状态下依然可以满足承载需求，可达到锁紧系统最初设计的各项性能指标，而且结构简单、工艺新颖、生产成本低，并且其独特的结构还能消除装置在加载时所出现的局部应力集中现象。

3） 六面体单元网格所建立起来的锁紧系统有限元模型，在计算过程中节省了大量的计算分析时间，且应力和变形计算结果的准确性也得到了相应的提高，不但获得了各部位均匀过渡的有限元云图，还准确地计算出锁紧系统各关键部件的应力阈值，为验证锁紧系统的合理性提供了可靠依据。

［1］ 刘茜，南传立，万淑敏．基于有限元分析的压实机压实效果研究［J］．天津大学学报，2004，37（6）：501-504．

［2］ 夏盛来，何景武．基于工程应用的有限元网格划分研究［J］．飞机设计，2008，28（4）：10-13．

［3］ 董梅．有限元法在结构件强度分析中的应用［J］．指挥控制与仿真，2007，29（4）：114-117．

［4］ 平安，甘娥忠，于亚婷．有限元法—原理、建模及应用［M］．北京：国防工业出版社，2004．

［5］ 马爱军，周传月，王旭．Patran和Nastran有限元分析专业教程［M］．北京：清华大学出版社．2005．

［6］ 申瑞民，许彦青，张同珍，等．基于多代理的智能型远程教学环境研究［J］．计算机工程与应用，2002（4）：253-256．

［7］ 姚兴佳，张晨晨，单光坤，等．基于ANSYS的风力发电机机舱底盘的强度分析［J］．沈阳工业大学学报，2008，30（1）：3841．

［8］ 朱爱民，其木格，郑鑫．基于UG的轮毂结构可靠性分析［J］．机械工程与自动化，2010（1）：74-76．

Finite Element Analysis of Drilling Platform Locking System Based on A B A Q US

WANG Jiancai1，YANG Lidong2，TIAN Jun1，MA Shuyu1
（1．Bohai Equipment Liaohe Heauy Industry Com pany，Panjin124010，China；2．K airui Energy Co．，Ltd．，Panjin124010，China）

The locking system is a key component of offshore drilling platform，the reliability of the locking device is vital for the safety of platform．It is difficult to sim ulate its stress value and distribution accurately by using classicalmechanics．In order to verify the rationality of the locking structure，each component of the locking system ismeshed as hexahedral elements based on the A B A Q U S software，strength analysis of the locking device is finished based on the nonlinear analysis platform and checking the strength according to the calculation results．The results showed that，its strengthmeets the design requirements，at the same time it also provides the reliable data for the development of the locking system related products．

drilling platform；locking system；nonlinear；strength chec

TE951

A

10．3969／j．issn．10013842．2015．03．011

10013482（2015）03004804

①2014-10-12

王建才（1968-），男，甘肃武威人，高级工程师，主要从事石油钻机和海洋工程装备的研究，Email：wjclsnoi＠126．com。