一种基于邻域搜索机制的旅行商问题求解❋
2015-08-02阮姗娜陈俊风王思睿
阮姗娜,陈俊风,顾 菁,王思睿
(河海大学物联网工程学院,常州213022)
一种基于邻域搜索机制的旅行商问题求解❋
阮姗娜,陈俊风,顾 菁,王思睿
(河海大学物联网工程学院,常州213022)
旅行商问题是一个经典的数学组合优化问题,其广泛的工程应用背景促进了旅行商问题求解方法的快速发展。针对旅行商问题中最优路径的连接特点,提出了两种邻域搜索方法:邻域随机性搜索法和邻域概率性搜索法。这两种邻域搜索法对旅行商问题解的质量具有一定的提高能力,其中,为了加快搜索速度,在算法前期采用了循环倒置算子。实验结果表明算法在求解小规模旅行商问题时具有良好的寻优性能。最后将该算法与标准遗传算法结合,并进行了实验结果对比。实验数据显示结合后的算法搜索性能优于单一的两种优化算法,提高了算法搜索解的能力。
旅行商问题;邻域;随机搜索;概率搜索;循环倒置;最优路径
1 引 言
旅行商问题(Traveling Salesman Problem,TSP)是组合优化[1]中一个易于描述但至今尚未彻底解决的古老而又困难的问题,是著名的NP-hard[2]问题。旅行商问题在工程上具有广泛的实际应用背景,最早应用于校车路线的优化。目前旅行商问题已广泛应用于电路板设计、城市规划、交通运输、物流配送等领域。因此,对旅行商问题进行研究具有重要意义,一直以来受到学者们的大量关注,是组合优化领域中的研究热点。
针对目前不同的实际应用背景衍生出了多种不同类型的旅行商问题,如非对称旅行商问题、多旅行商问题、多目标旅行商问题、黑白旅行商问题等,它们都可以转换成旅行商问题进行求解。旅行商问题的求解方法主要分为以线性规划法、分支定界法为代表的精确算法[3-4]和以启发式算法为代表的近似算法[5-6]。近似算法求解性能优于精确算法,应用性也比精确算法广。通过观察旅行商问题中最优路径图的每个城市连接特性后发现,利用邻域搜索机制、对各个城市的邻域进行深度寻优的思想对旅行商问题的求解找到了一个合适的近似算法。
2 TSP描述
TSP最早可追溯到18世纪骑士周游问题,又称旅行推销员问题[7]。
TSP可描述为:推销员打算到n个城市进行产品推销,从其中一个城市出发,要求找到一条通过所有城市再回到起点的最短路径,每座城市必须且只能访问一次。
设n个城市集合为

城市之间的距离为

则上述问题转化为如下优化问题:

其中kij为

图论语言描述则为:一个带权图G=(V,E),V={1,2,…,n}表示顶点集,E={eij=(i,j),i,j∈V,i≠j}表示边集,寻求G的一个使边长最小即权值最小的Hamilton回路[8]。
3 邻域搜索
通过对最优路径图研究后发现,依据总体路径最短的特征,每个城市在离自己距离较近的多个城市内选择合适的城市进行连接。并非所有城市都与自己的最近邻城市连接。若所有城市选择与最近邻的城市相连,路径很容易陷入局部最优。因此本文根据最优路径各城市的这种连接特点,提出两种新的邻域搜索法,避免算法过早陷入局部最优。
3.1 邻域范围内随机搜索
当前所有N个个体的集合记为U={u1,u2,……,uN},对每个城市找出与其相邻比较近的n个城市作为一个集合C={c1,c2,……,cn},n的个数选择对最优解的寻找有很大影响。针对当前城市i,在由n个城市组成的邻域范围内利用随机选择方式进行下个城市j的选择。若C中所有城市都已被遍历过,则选择不包含在C内、并离i最近的城市j作为下个城市访问点,避免城市连线出现交叉现象。
3.2 邻域范围内概率搜索
对于每个城市,找出与其相邻较近的n个城市作为一个集合C,同时计算整体U的平均路径长度。为了防止路径过大的个体影响整体的平均值,在计算平均值时去除路径最大的个体。统计路径长度小于平均值的个体总数k。对于路径长度小于均值的k个个体,统计与城市i相邻的集合C中每个城市出现的次数m,计算C中每个城市出现的概率p=m/k,根据轮盘赌选择方式选择下一个访问城市。若下个访问城市的概率为0,则对为0的城市概率做归一化处理,保证每个城市都可能被访问到,防止最优解被丢失。
4 循环倒置算子
为了加快前期寻找最优解的速度,在算法初期采用了倒置算子[9],即随机选取个体中的城市片段进行倒置,若倒置后个体的距离小于原先个体,则用新个体替换原先个体。为了不失去统一性,将个体中所有城市构成一个循环圈,首尾附近的城市片段也可参与倒置操作,避免局部最优城市片段的丢失,增加搜索到最优解的概率。
5 算法结构
根据以上描述,本文算法的基本结构如下:
(1)初始化:随机生成N个个体,保持整体多样性。设置最大进化迭代次数。
(2)算法前期:采用循环倒置算子,使群体较快收敛到最优值附近,实验中前期的代数设为最大进化代数的1/5。
(3)算法中期:循环倒置算子和邻域搜索法共同进行,增加寻优速度,提高寻优概率。实验中中期的代数设为最大进化代数的2/5。
(4)算法后期:利用邻域搜索法在全局中逐步寻找最优解。
(5)终止条件:当达到最大迭代次数时算法停止,若没有达到则返回到步骤(2)继续迭代。
6 实验结果与分析
实验中用matlab.R2012a软件实现算法对TSP的求解。初始化设置个体总个数为30,最大迭代次数400,TSP城市采用TSP数据库中的burma14(最优解为30.8785)。针对不同的邻域城市个数n进行多次测试,实验结果如表1所示。其中Ave表示程序运行10次后得到的平均值,Opt表示10次中得到的最优值,K表示10次中得到最优值的次数。

表1 RSN和PSN在不同的n条件下得到的实验结果
由表1可知,邻域搜索法在n为2到6时都可寻到最优结果,但随着邻域个数的不同,得到的平均值不同,搜索到最优值的次数也不相同。对于随机性邻域搜索,当n=5时寻优效果最佳;对于概率性邻域搜索,当n=4时寻优效果最佳,并且概率性邻域搜索成功率高于随机性搜索成功率。
根据以上实验结果,对标准的30个城市(最优解为423.7406)进行了测试。邻域城市个数n分别为4、5和6,个体个数仍为30,最大迭代次数为800。由于遗传算法具有全局性,最后将该算法的两种情况分别与标准遗传算法(SGA)结合,设置SGA的变异概率为0.05,交叉概率为0.9,种群大小为30,最大迭代次数为800代。得到的实验结果如表2所示。
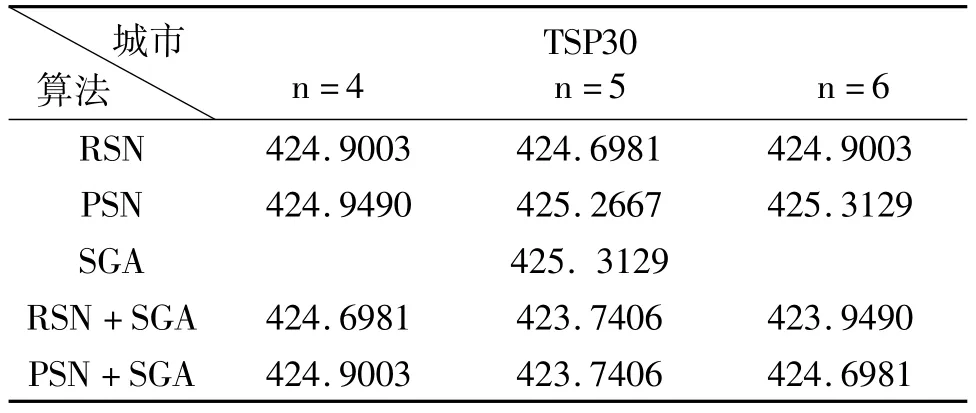
结合后得出的实验结果表2 不同n条件下RSN和PSN与SGA
由表2可知,邻域随机搜索比概率寻优效率高,但算法单独运行时易陷入局部最优。针对不同的城市规模应设置不同的邻域城市个数。该算法与SGA结合后在n=5时寻到了最优解,提高了算法搜索效率,使得解的质量得到了相应提高。
观察表1和表2可知,此算法对于小规模的TSP搜索效果较好。与其它算法融合提高了算法搜索性能,增强了寻优能力。但在实验过程中总运行时间偏慢,因此该算法在运行速度上有待进一步加强。
7 结束语
基于邻域搜索机制的旅行商问题求解主要是针对TSP中最优解的城市连接规则,在邻域范围内根据随机寻优和邻域范围内概率寻优的方法来求解TSP,实验结果说明其具有一定的寻优能力,并且与其它智能优化算法的结合有助于算法性能的提高,因此本文方法与其它算法的融合将是下一步值得继续研究的方向。
[1] Lenstra JK,Kan A H G R,Shmoys D B.The traveling salesman problem:a guided tour of combinatorial optimization[M].New York:Wiley,1985.
[2] Garey M R,Johnson D S.Computers and Intractability:a guide to the theory of NP-Completeness[M].San Francisco:Freeman W H,1979.
[3] 杨忠程,徐新黎,叶双挺.基于组合拆分策略求解TSP的动态规划算法[J].计算机工程,2012,13(38):185-187.
YANG Zhong-cheng,XU Xin-li,YE Shuang-ting.Dynamic programming algorithm based on combination and Division Strategy for Solving TSP[J].Computer Engineering,2012,13(38):185-187.
[4] 周康,强小利.求解TSP算法[J].计算机工程与应用,2007,43(29):43-47.
Zhou Kang,Qiang Xiao-li,Tong Xiao-jun.Algorithm of TSP[J].Computer Engineering and Applications,2007,43(29):43-47.
[5] Tang Q,Zeng J Y,Li H.A particle swarm optimization algorithm based on genetic selection strategy[M].Springer Berlin Heidelberg:Advances in Neural Networks ISNN 2009,2009.
[6] Gao S,Zhang Z Y,Cao C G.A novel ant colony genetic hybrid algorithm[J].Journal of Software,2010,5(11):1179-1186.
[7] 马良.旅行推销员问题的算法综述[J].数学的实践与认识,2000,30(4):156-165.
Ma Liang.Algorithmic review on the travelling salesman problem[J].Mathematics in practice and theory,2000,30(4):156-165.
[8] Garey M R,Johnson D S,Tarjan R E.The planar Hamiltonian circuit problem is NP-complete[J].SIAM Journal on Computing,1976,5(4):704-714.
[9] 朱林杰.基于TSP的遗传算法优化研究[D].大连:大连理工大学,2007.
Zhu Lin-jie.The study of genetic algorithm optimization based on TSP[D].Dalian:Dalian University of Technology,2007.
Solution to Traveling Salesman Problem Based on Neighborhood Search System
Ruan Shanna,Chen Junfeng,Gu Jing,Wang Sirui
(College of Internet of Things Engineering,Hohai University,Changzhou 213022,China)
Traveling salesman problem,as a classic mathematical optimization problem,with the extensive background of engineering application,promotes the development of the solution methods.For the connected characteristics of the optimal path of the traveling salesman problem,this paper puts forward two kinds of neighborhood search methods,i.e.the random search method in the neighborhood and probabilistic search method in the neighborhood,which improve the quality of the solutions.Among them,in order to speed up the search speed,loop inversion operator is used in the early process of the algorithm.The experimental results show that the algorithm has a good optimization performance when solving traveling salesman problem with small scale.Finally,the proposed algorithm is combined with the standard genetic algorithm and compared with the standard genetic algorithm.The experimental data shows that the combinational algorithm is better than the single optimization ones and improves the searching ability.
Traveling Salesman Problem;Neighborhood;Random search;Probabilistic search;Loop inversion;Optimal path
10.3969/j.issn.1002-2279.2015.06.012
TP301.6
A
1002-2279(2015)06-0044-03
国家自然科学基金(61403121)
阮姗娜(1990-),女,安徽省池州市人,硕士研究生,主研方向:智能信息处理。
2015-03-18
