一种电荷再分布的逐次逼近AD转换器设计

高加亭，赵宏建

（中国电子科技集团公司第四十七研究所，沈阳110032）

一种电荷再分布的逐次逼近AD转换器设计

高加亭，赵宏建

（中国电子科技集团公司第四十七研究所，沈阳110032）

设计了一种电荷再分布逐次逼近AD转换器电路。通过引入耦合电容CS，整个电容阵列只需要128个单位电容C，相比直接使用二进制加权电容阵列，节省了近97%的单位电容数量。选用Charted 0.35μm Mix Signal，3.3V工艺模型进行设计，仿真结果表明，转换器的分辨率LSB＝0.6mV，能够达到12位转换精度。

逐次逼近；模数转换器；数模转换器；电荷再分布

1 引 言

模数转换器（Analog－to－Digital Converter，ADC）将模拟信号转换成数字信号，是模拟系统与数字系统接口的关键部件，长期以来一直被广泛应用于雷达、通信、测控、医疗、仪表、图像和音频等领域。与其他几种ADC相比，逐次逼近ADC具有中等转换精度（一般8～16位）和中等转换速度（一般5MS/s以下），采用CMOS工艺制造时可以保证较低的功耗和较小的芯片面积，而且易于实现多路转换，因此在精度、速度、功耗和成本方面具有综合优势，市场应用广泛［1］。

2 电荷再分布逐次逼近ADC设计与分析

使用最普遍的逐次逼近ADC之中，DAC部分采用基于电荷再分布原理电容阵列结构［2］。如果仅仅使用并行二进制加权电容阵列，那么12位DAC需要4096个单位电容，这会大大增加芯片面积，提高成本［3］。所以一般高位数的ADC采用分段式结构，传统的分段式将其补偿电容放在低权位电容阵列，耦合电容CS的取值应使低权位电容阵列的电容之和与其串联之后的等效电容为一个单位电容，采样阶段是对所有的权电容都进行电荷采样，如图1所示。

但是CS这样一个小数值的电容在版图设计时会遇到布局问题：如果用单位电容通过串并联的形式组成耦合电容，由于用到的单位电容个数较多，电容的下极板寄生效应会严重影响SAR ADC的线性度；如果用一个比单位电容大一些的电容作为这个耦合电容，则在电容阵列中会出现不匹配现象［4］。

为了克服上述各种电容阵列的困难，改进的分段电容结构阵列可以同时避免分数电容值和悬浮节点的产生。改进型的分段电容阵列SAR ADC如图2所示。与传统的分段电容阵列不同的是，将其补偿电容在高权位电容阵列，此时耦合电容Cs的大小等于单位电容C0，C1－C6与C7－C12分别是两个二进制加权的电容阵列，下面来具体分析工作原理及过程。

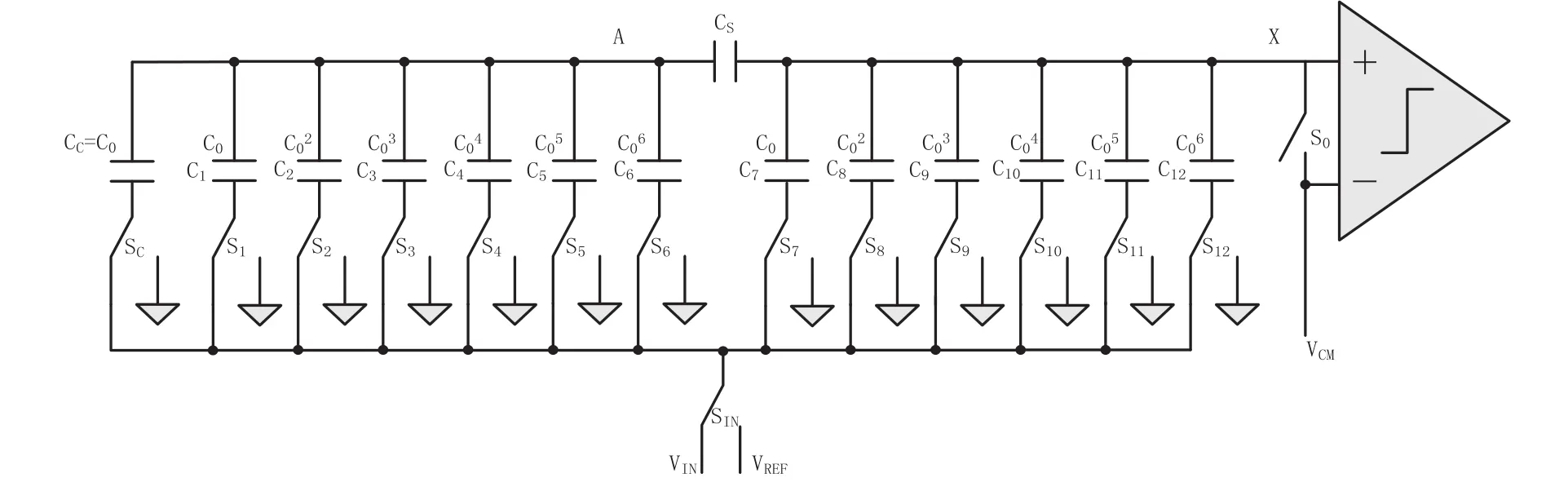
图1 传统的逐次逼近ADC电路原理图Fig.1 Traditional schematic of SAR ADC

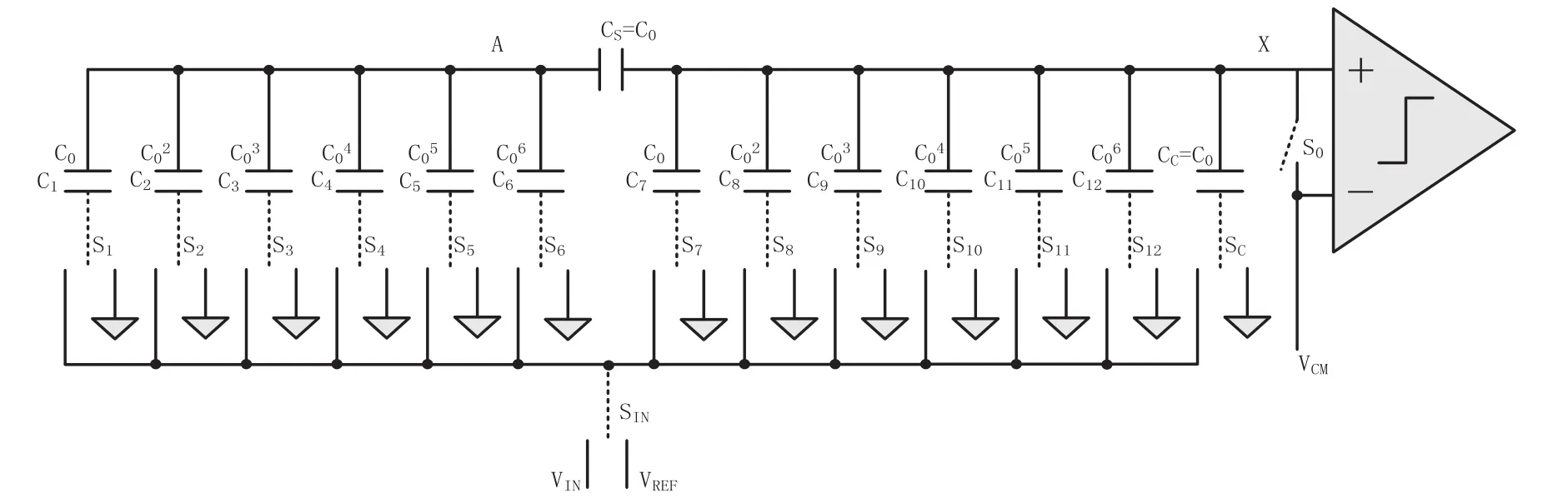
图2 逐次逼近ADC电路原理图Fig.2 Schematic of SAR ADC

（1）采样阶段

只对高位段MSB段进行采样，将开关SIN与VIN闭合，开关SC、S12－S7使电容C0、C12－C7下极板与VIN相接，而开关S0闭合，使它们的上极板与固定电压VCM相接，开关S6－S1使电容C6－C1下极板与地相接，电荷存储在高位电容C12－C7，CC以及低位电容和CS的串联等效电容上，电荷数量为：

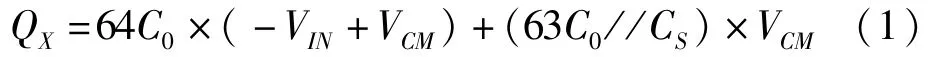
（2）保持阶段

S0断开，SIN与VREF闭合，开关SC、S12－S7以及S6－S1都与地闭合，DAC输出电压为：

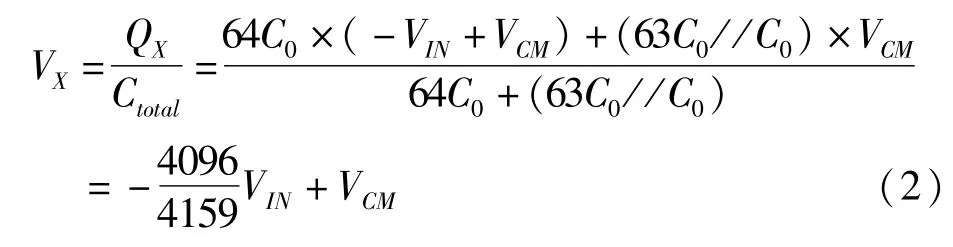
（3）电荷再分配阶段

先将第12位（即MSB）置1，即通过S12将C12的下极板连接到VREF，通过等效电路如图3（a）所示，因为X点总电荷数不变，可以得到：

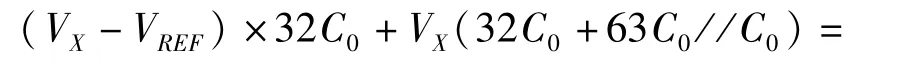
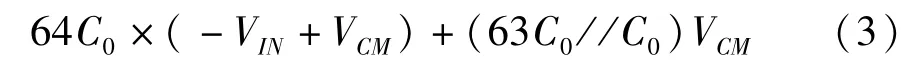
所以DAC输出电压为：

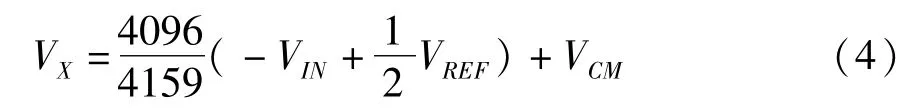
如果VIN＞1/2VREF，那么比较器输出0，保留第12位为1，否则第12位清0。

依次类推，直到确定了第1位（即LSB），等效电路如图3（b）所示，由于A点的电荷代数和为0，所以有：

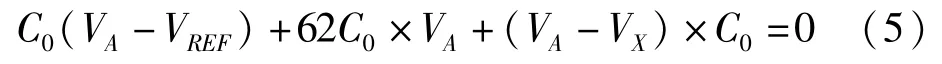
X点的电荷数有：

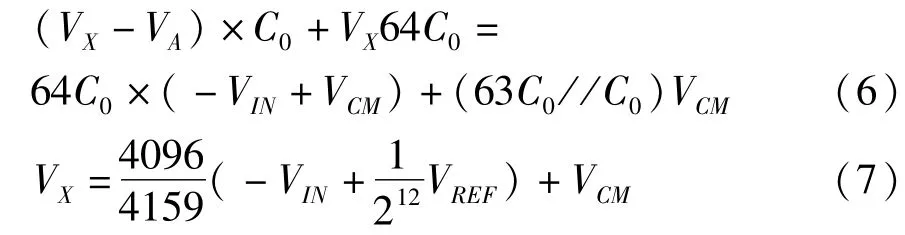
最终，该分段电容结构DAC的输出为：

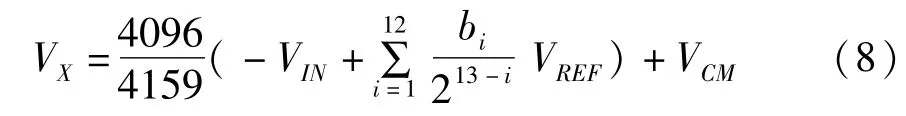
其中，bi是该分段电容结构DAC的第i位值，为0或1。

可见，表达式中仅仅多了一个略小于1的系数，只要设计比较器的分辨率大小足够分辨出带有系数的最小精度，对于A/D转换器的功能以及性能并没有影响，不影响其线性度。该改进的全二进制加权分段电容阵列结构不仅仅减少了整个芯片的面积，而且所有电容都为单位电容的整数倍，方便了版图设计和电容匹配。

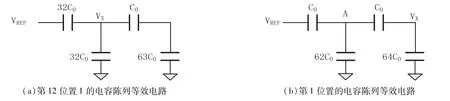
图3 电荷再分配等效电路Fig.3 Equivalent circuit of charge redistribution

3 电路仿真结果

使用Charted 0.35μm Mix Signal，3.3V工艺模型进行电路设计，在电源VCC＝3.3V，VREF＝2.5V的情况下，对逐次逼近ADC中电容阵列进行扫描，可以得到其输出特性曲线如图4所示。

图4 电容阵列输出特性曲线Fig.4 Output characteristics of CDAC

放大其中一段得到图5，LSB＝0.6mV，与理论计算的VREF/4096基本相等。

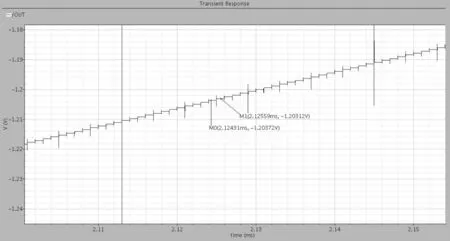
图5 输出特性曲线局部Fig.5 Part of CDAC output characteristics

通过仿真对ADC的理论计算进行验证，仿真波形如图6所示，从仿真波形来看，ADC能够达到12位转换精度，转换结果与理论计算相同。

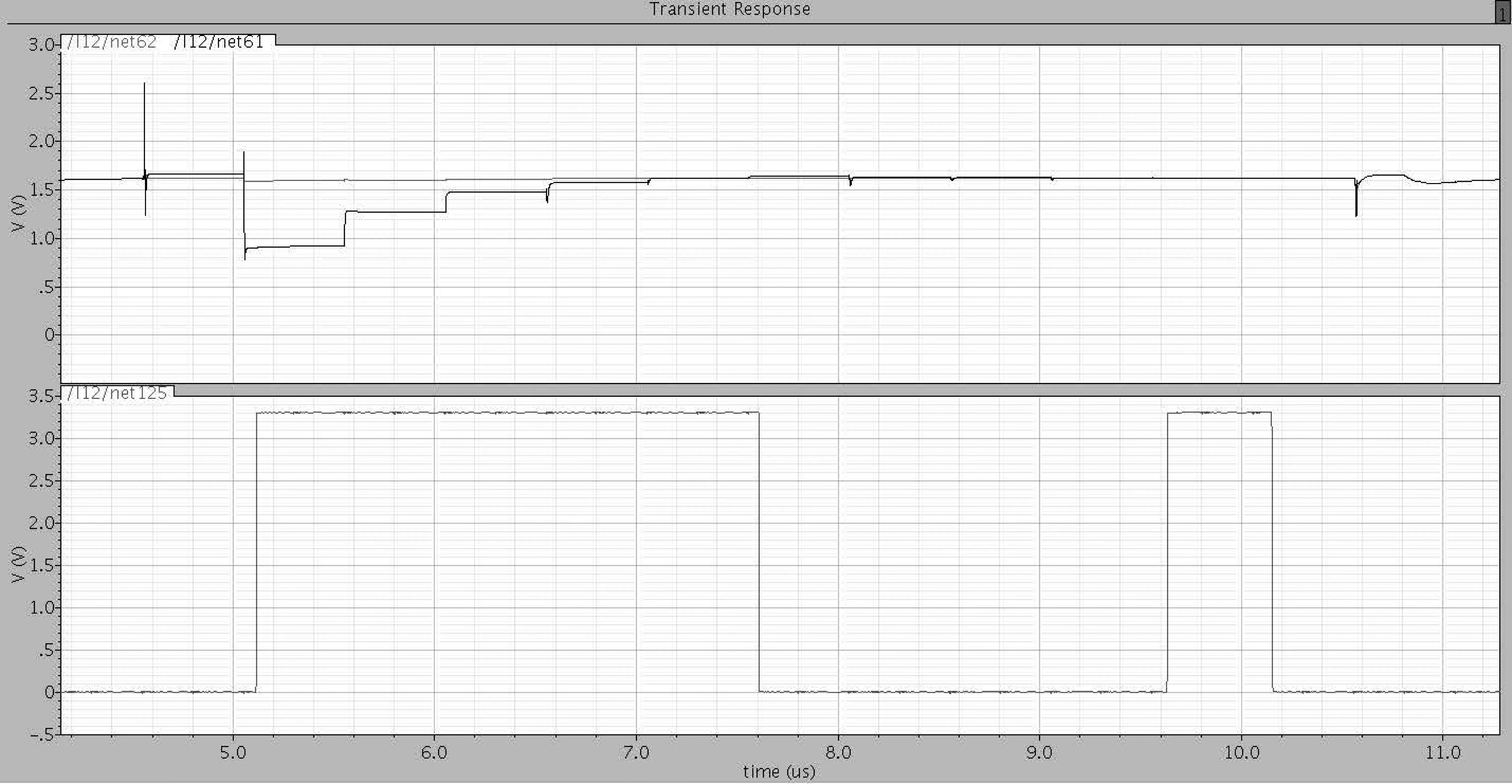
图6 逐次逼近ADC仿真结果Fig.6 Simulation result of SAR ADC

4 结束语

设计的电荷再分布逐次逼近ADC，通过引入耦合电容，整个电容阵列只需要128个单位电容C，相比直接使用二进制加权电容阵列，节省了近97%的单位电容数量。分析了外加耦合电容CS的计算方法和采样保持转换的原理，通过仿真分析，转换的分辨率LSB＝0.6mV，能够达到12位转换精度。

［1］ 孙彤.低功耗逐次逼近模数转换器的研究与设计［D］.北京：清华大学，2007.

SunTong.Study and Design of Low－power Successive Approximation Analog－to－digital Converter［D］.Beijing：Tsinghua University，2007.

［2］ Takeshi Yoshida，Miho Akagi，Mamoru Sasakiand Atsushi Iwata.A 1V Supply Successive Approximation ADC with rail－to－rail input voltage range［C］.IEEE，2005：192－195.

［3］ Eugenio Culurciello and Andreas Andreou.An 8－bit，1mW Successive Approximation ADC in SOICMOS［C］.IEEE，2003：301－304

［4］ R.Jacob Baker.CMOS电路设计·布局与仿真［M］.刘艳艳，张为，译.北京：人民邮电出版社，2008.

R.Jacob Baker.CMOSCircuit Design，Layout，and Simulation Second Edition［M］.Beijing：ThePeople’s Posts and Telecommunications Press，2008.

Design of Charge Redistribution SAR DAC

Gao Jiating，Zhao Hongjian
（The 47th Research Institute of China Electronics Technology Group Corporation，Shenyang 110032，China）

The charge redistribution successive approximation analog－to－digital converter is designed in this paper.By adding coupling capacitance CS，128 unit capacitances C are used in the capacitor array，and almost 97%unit capacitances is saved comparing with the directly using binary weighted capacitor array.The simulation is completed by 0.35μm Mix Signal，3.3V processmodel in Charted and the results show that the resolution of the converter（LSB）is 0.6mV and can reach 12 bits conversion accuracy.

Successive approximation；ADC；DAC；Charge redistribution

10.3969/j.issn.1002－2279.2015.06.002

TN752.2

A

1002－2279（2015）06－0006－03

高加亭（1982－），男，吉林省农安市，本科，工程师，主研方向：集成电路工程。

2014－12－17