由一道题的“错误”中读懂的
2015-07-29郭建军
郭建军
那次小测试是在刚教学完《长方体和正方体》单元之后进行的。没有进行任何复习,就是想看看学生在学完这个单元之后的薄弱点在哪里。揣着这样的想法,进行了测试。一共12道题,同学们可以选做10题,每题10分,共100分。
测试中有这样一道题:一个长方体的侧面积是360平方厘米,高是9厘米,长是宽的1.5倍,求它的表面积。就是这一题,让我出现了从教以来从没有出现过的窘况,全班65人没有一个人做对。
32人这样做:
宽:360÷9=40(厘米)
长:40×1.5=60(厘米)
表面积:(60×40+60×9+40×9)×2
=(2400+540+360)×2
=3300×2
=6600(平方厘米)
9人这样做:
宽:360÷2÷9=20(厘米)
长:20×1.5=30(厘米)
表面积:(30×20+30×9+20×9)×2
=(600+270+180)×2
=1050×2
=2100(平方厘米)
8人未选做这一题。
16人出现错误,学生的错误有两种类型:一类属于求表面积的方法跟求体积的方法混淆:另一类属于计算错误。
如果换一个角度来统计,这65个人中,求长和宽时有20人将右侧面(或左侧面)面积当成360平方厘米来求宽:有37人将左右两个侧面的面积当成360平方厘米来求宽。
其他题都答得还不错,唯独这一题让我觉得不可思议,不知道多少测试中,从来没有哪一题是全班全错的。带着心头的疑惑。去看了看其他班级的情况。结果,其他班级也是这样,没有一例正确。
何为侧面积?侧面积的定义为:正方体、长方体、圆柱体等除掉上、下底面积之外的面就是侧面积,让我们成年人来思考这个问题,没有困难。学生对侧面积的理解出现错误。而且是这样大面积的问题,我也一直在思考着,到底是什么原因会出现这样的错误呢?教学时,没有解释清楚?同学们听得不够认真?
教学时,曾经有这样一题:
一个长方体饼干盒。长17厘米,宽11厘米。高22厘米。如果在它的侧面贴满一圈包装纸(如右图)。包装纸的面积至少有多少平方厘米?
回忆当时上课时的情景,这道题是学生自己进行分析的。当时,一个学生抓住了关键词语“一圈”来分析,要求“贴满一圈包装纸”实际上就是要我们求前、后、左、右四个面的面积。求包装纸的面积这一问题轻而易举地被同学们解决了,我用手势点了一下“侧面”表示的一圈商标纸的含义,因为想到这个时候同学们刚刚学习长方体的侧面问题,没有过于强调长方体的“侧面”就是指前后左右四个面的面积。这就是问题所在。
顺着学生的错误去思考。近些年来,一直任教六年级,往后续的知识点思考,六年级下册会学习圆柱的侧面积,圆柱的侧面是一个曲面,展开后是一个长方形(或平行四边形),那么要求圆柱的侧面积,转换成求长方形的面积或者平行四边形的面积就可以了,如果学生学习长方体的侧面积时,能用这样的方式来理解,那也就不难了,可这是后续的知识,现在呈现也不合适。再往六年级以前的知识去思考,“侧面”这一词语在学生的最近发展区里到底在哪里出现过呢?好熟悉的词语。仔细思考后发现,在教学《观察物体》这一单元时,有过“侧面”这一词语,曾经还解释过“左侧面”和“右侧面”。
找到学生错误的源头之后,试着再思考怎样纠正这样的错误,而且能够利于同学们自己将掌握的知识进行一次清晰的梳理呢?我决定,将问题直接抛给他们,让他们自己去思考解决问题的办法。这样做了决定之后,就有了第二天课堂中同学们相互补充的热闹情景。
课始,我出示了一个长方体。学生们很轻松地辨别它上下面、前后面、左右面,标上最多只能看到的三个面。
顺着学生们的“错误”进行追问。
师:这时我们还可以把“右面”称作什么?
生1:侧面。
生2:准确地说应该是“右侧面”。
师:好一个“右侧面”,相对应的还应该有……
生1:还应该有“左侧面”。
生2:侧面分为“左侧面”和“右侧面”。
(我心里明白。这是学生们用曾经学过的知识进行的比较完整的理解。于是,我把这幅图进行了顺时针90°旋转)
师:从我这个小小的动作中,你有什么发现吗?
生1:这样一转,刚才的前面就变成了现在的右面,后面就变成现在的左面了。
生2:也可以说,左面变成了前面。右面变成了后面。
生3:我来补充,其实也就是刚才的前后——左右面,变成了现在的左右——前后面了。
师:那我们现在可以把哪两个面称为“侧面”呢?
生:现在的左右面,也就是刚才的前后面。
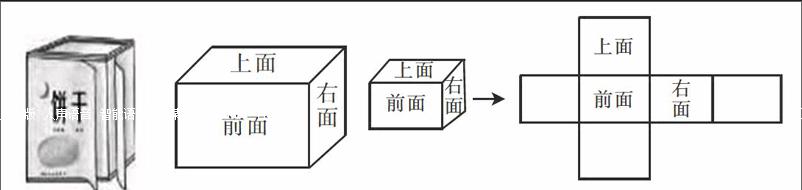
师:(出示展开图)也就是说,如同这幅图一样,左右面我们可以将它们也称作“侧面”。但是,如果我们放的位置不同,它们的左右面会像刚才一样调换。
同学们表现出豁然开朗的样子。
这一片段中,悄悄地运用同学们的错误,“将错就错”。巧妙的引导成为已有知识和将学知识联系的桥梁。
生1:还可以这样来理解:要求侧面积只要先求出前面和右面的面积,然后乘2就可以了。
生2:也可以求前后左右四个面展开之后的长方形的面积。如果设一个长方体的长、宽、高分别为a、b、h,那么,它的侧面积就是2(ah+bh)。
生3:也可以这样来理解,要求长方体的侧面积,知道长方体的底面周长和高,把它们相乘起来就可以了。用公式表示长方体的侧面积就是:长方体的侧面积=(长+宽)×2×高。
生4:用字母来表示这个公式:S=2(a+b)h。
惊诧于学生们的思考的同时,我也有了对自己教学的思考。作为老师。我们在进行每节课的教学之前,必须做到以下几点。
一、吃透教材
2011年版课标配套教材,不仅图文并茂、生动有趣,呈现方式也更加丰富开放,删除了旧教材“繁、难、偏、旧”的知识。还结合学生认知发展的特点。对原有的知识点进行了整合、重构。这需要我们认真研究新旧教材的变化,把握教材变化的本质。
教材,是教师教和学生学的最基本的依据。它承载着数学知识与技能、数学思想与方法、解题策略等人类文化的结晶。面对静态的数学文本,在教学前,我们先不要忙着看教参。而是要毫无遗漏地读出每页教材中呈现的所有信息,揣摩编者安排这些信息的意图,弄清楚数学知识的内在逻辑顺序,有针对性地设计各个教学环节。“挖”出它的重点、难点;“挖”出它外显的知识和其中的内隐。
再读教材时,对于每节课的教学内容,我们不仅要做到“入乎其内,出乎其外”,创造性地使用教材,放大教材的功能,还要能“既见树木,又见森林”,联系整册教材来解读本课教材。根据课程标准、教参等来确定它在本节课的教学中承担的具体任务,明确本节课到底要教给学生哪些知识。(如:针对文中的这道错题。在教学“长方体饼干盒”那道题时就联系长方体“侧面”的含义进行教学,考题中的错误也许就不会存在了。)对教材进行适度整合和拓展,清楚地知道本节课应该把学生教到什么程度,训练学生的什么能力,培养学生怎样的情感、态度与价值观,等等。
因此,在进行每节课的教学之前,必须努力研读教材,为师生一起走进新教材、实践新教材打下良好的基础。
二、研透教法
每一课的教学之前,我们应作这样的思考:本节课的知识源于学生哪些已有的知识经验、生活经验以及思维经验?如何有效激活学生的这些已有经验?设计哪些让学生能经历自主发现、选择和确定问题,主动应用知识解决问题的学习活动?在设计教学的过程中,我们应关注学生的数学思考,组织学生参与活动的全过程,通过数学地提问、数学地思考、数学地交流。引导学生用数学的思维方法去观察、分析、解决现实问题,积累数学活动经验,真正做到为形成学生的数学素养而教。让教学具有主体性、活动性、趣味性、思考性、开放性等特点。我们的教学方法也应是丰富多彩的,如自主式学习、合作式学习、探索式学习、提问式学习等。只有这样。我们才能在课堂上呈现各具特色的学习方式,使学生寓学习于快乐的探究之中,教学的过程也才能以主动探索为主线,引导学生在动手实践、合作交流的过程中,体会数学思想方法。
三、读懂学生
学生是学习的主体,我们所教学的内容。最终只有被学生所理解,才能真正体现其蕴含的数学价值。在教学之前。教师可以通过适当地转换角色,把自己当作学生,站在学生的角度阅读文本、解读文本,体验学生阅读文本过程中会有哪些发现,或者会遇到哪些问题,在这一基础上再设计恰当的、可行的学习活动。在读懂学生的基础上,实现学生最大程度的发展。
小学数学课堂应当是师生共同经历的“协同合作”的课堂。作为老师,我们应注重教学活动的趣味性。创设宽松、自由、民主的活动氛围,不断以欣赏的眼光观察学生,不断地给学生以激励性的评价,让学生始终保持旺盛的学习热情,在学习活动中感受到数学学习的快乐。在激发学生浓厚的数学学习兴趣的同时,注重引导学生努力寻找所学知识之间的联系。比如,在教学“立体图形”时,要能恰到好处地引出立体图形与平面图形的联系。引导学生感受数学中的转化思想。
总之。为了学生,我们应通过丰富多彩、形式多样的活动。让学生愿意亲近数学、了解数学、学习数学,并对数学保持一定的好奇心。在课堂上真正做到关注学生,促进学生主动地、个性化地学习。在活动过程中。通过对活动过程的回顾,启迪学生思考、交流活动体会和收获。使他们对数学有一个较为全面、客观的认识。从而发展学生的智慧,发掘学生的潜力,培养学生的多种能力和合作精神,引导学生学会数学学习的方法,激发学生的创造性和数学的应用意识。
