读懂教材、读懂学生与教学决策

齐云

一、教材分析

本课教材有几个非常明显的特点：

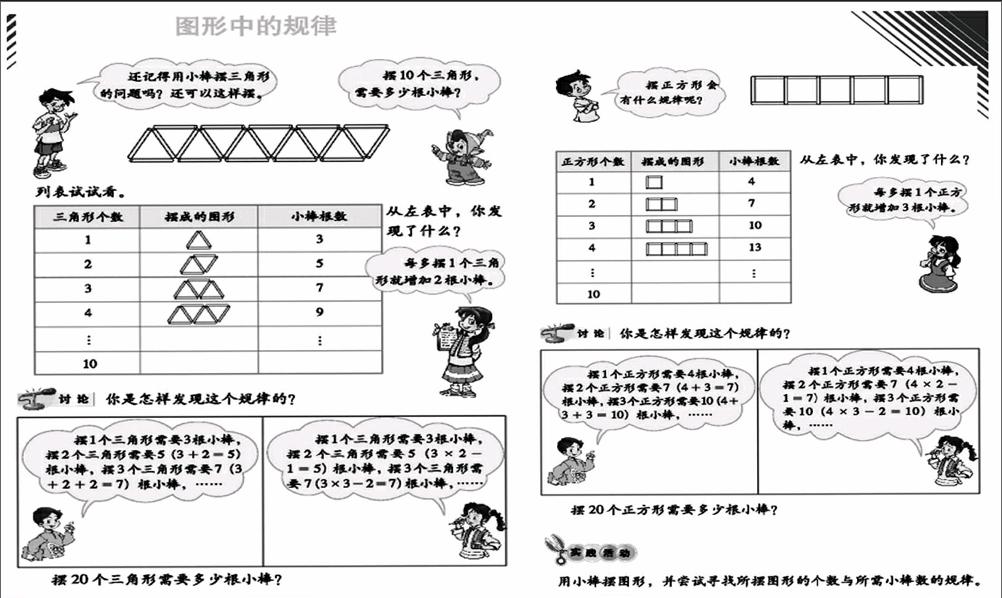
（1）精心选择了学生熟悉的图形（三角形、正方形）作为探索规律的载体，所创设的问题情境具有一定的探索空间，学生跳一跳够得着。

（2）两个问题均有利于学生借助动手操作，利用图形的直观性，建立图形与数量之间的对应关系，发现图形中的规律。

（3）两个问题特别适合体现以简驭繁（以小见大）、先退后进的问题解决策略，适合让学生经历由特殊到一般的问题解决过程，从中积累数学活动经验。

（4）教材提示了两种方法。前一种（方法一）的数学背景是等差数列的通项公式：a_n=a₁+（n-1）×d。后一种（方法二）是基于将n个三角形或正方形连起来摆成一行，比分开来要节省（n-1）根小棒。

（5）教材没有提出用含字母的式子表示规律的要求。

（6）教材留出了进一步发展的空间。在解决了摆三角形、正方形两个问题的基础上，还可以拓展，提出“把五边形、六边形连起来摆成一行要多少根小棒”的问题，让学生自己类推。

二、学情分析

（1）学生已认识了常见的平面图形，知道三角形有三条边、正方形有四条边，对本课的学习有了知识上的准备。

（2）四年级学生有一定的动手操作经验和探究规律的经历，但在规律的归纳、概括与语言表达方面，存在较大的个体差异。

（3）在先前的学习中，学生已经有了以小见大、先退后进的问题解决经验。在学习用字母表示数时，也有了由特殊到一般的抽象经历。

（4）教材给出的方法一，学生通过用小棒摆图形的操作就能发现。而方法二。则需要从整体的角度去观察、思考，才能想到“连起来摆一行”节省了几根。

（5）要解决“摆20个三角形（正方形）要多少根小棒”的问题，依次递推太麻烦，需要总结规律。能用日常语言叙述规律的学生，让他们用字母表示困难不大。但他们化简含字母的式子的能力有限，对于同一规律的不同表示形式，如3+2（n-1），3n-（n-1）与2n+1，一般学生还不能认识到它们之间的内在联系。

（6）拓展性问题“把五边形、六边形连起来摆成一行要多少根小棒”处在多数学生的最近发展区内。

三、教学对策

1 基于学生的认知能力差异，创设冲突，多元理解

（1）设疑——创设认知冲突

首先，教师设问：摆1个三角形要3根小棒，摆2个三角形呢？有的学生说要6根，也有的学生说5根。由此，很自然地引出连起来摆一行“节省”1根。这就为理解教材的后一种解法作了铺垫。

其次，让学生独立操作、填表，得出摆4个三角形需9根小棒后，直接提出“摆10个三角形要多少根小棒”的问题。迫使学生跳出依次递推的局限，寻找规律，思考算法。

（2）开放——多元理解

给学生足够的时间和空间自主探索，鼓励学生寻找不同方法，让学生在小组内交流自己的想法。说不清楚，看课本的提示。

全班交流不同算法，如3+2×9，3×10-9。教师追问：“这个9是哪里来的？”引出3+2×（10-1），3×10-（10-1）。

如果有学生说出10×2+1或1+10×2。同样追问：“为什么是10×2？加1是加哪一根？”

这样，既诱导学生清晰地描述规律，又使其他学生理解不同的思路。

2 基于学生的观察变换能力，数形结合，深入浅出

数形结合既是常用的数学思想方法，也是数学教学中帮助学生理解的主要手段。本课采用多媒体课件动态演示，借助几何直观，将各种方法形象、生动地呈现在学生眼前，使没想到的学生也能看明白。

方法一的直观解释：第1个三角形用3根小棒。每增加一个三角形就增加2根小棒。

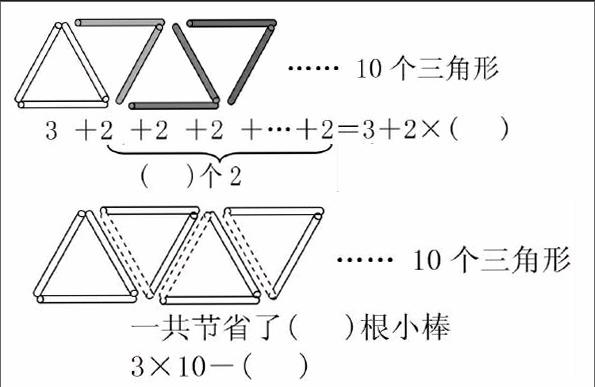
方法二的直观解释：摆几个三角形，先出示几个3根，再去掉“节省”的小棒。

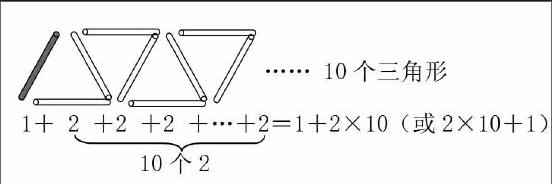
方法三的直观解释：

总之，在学生独立探索、交流的基础上，加以课件演示，数形结合这一数学思想方法得以彰显，有效地帮助学生加深了对规律的理解。

3 基于学生的符号表达水平，以退为进，逐步抽象

用字母表示数是小学数学中一个相当重要的知识，它的出现意味着数学发展的飞跃，从算术走向代数。然而在今天看来非常简单的“字母表示数”，在人类认识过程中却经历了上千年的漫长孕育，最终由法国数学家韦达首先有意识地系统使用，从而有力地推动了数学的发展。

聚焦到四年级学生身上，他们已经习惯了数的具体性与唯一性，因此在初学用字母表示数阶段，用含字母的式子表示图形个数与小棒根数之间的数量关系对部分学生来说，有一定的难度。

为帮助有困难的学生，采取了逐步抽象的对策：

进而，摆10个三角形：3+2×（10-1），摆n个三角形：3+2×（n-1）

至于3+2（n-1），3n-（n-1）与2n+1等不同表达式之间的内在联系，则留给学有余力的学生课后去探究。

4 基于学生的最近发展区，适当拓展，启发类推

由于学生有了探索三角形个数与小棒根数之间关系的经验，所以接下去就放手让学生自己探究正方形个数与小棒根数的关系。教师巡视指导，学生交流汇报。

然后，再加以发展，逐步构建递进的认知序列：

如上图，连续摆n个三角形需要小棒是2n+1根；

连续摆n个正方形需要小棒是3n+1根；

连续摆n个正五边形需要小棒是（ ）根；

连续摆n个正六边形需要小棒是（ ）根。

实践表明，绝大多数学生能够拾级而上，推出小棒根数的规律与表达式。