基于布里渊散射的分布式光纤传感信息提取方法

吴娟娟，石贵民，胡绍斌，吴龙怀，林陈楠（武夷学院 数学与计算机学院，福建 武夷山 354300）



基于布里渊散射的分布式光纤传感信息提取方法

吴娟娟，石贵民，胡绍斌，吴龙怀，林陈楠
（武夷学院 数学与计算机学院，福建 武夷山 354300）

摘要:通过深入研究分布式传感光纤的机理，分析、比较了三种不同的BOTDR的特点和应用，剖析了布里渊散射分布式光纤传感技术在信息安全领域的应用价值；在LabVIEW软件平台上针对于累加平均算法实现了仿真实验，同时利用MATLAB实现了基于Morlet小波变换仿真；实验结果在一定程度上为深入探索布里渊分布式光纤传感系统提供了参考依据。

关键词：光纤；传感技术；布里渊散射；LabVIEW

传统的分布式传感技术发展完善，但是在检测空间分辨率等参数时存在着传感距离的问题。传统的方法在检测时存在着或多或少无法避免的弊端：封装庞杂、不能完成随时检测等问题。基于布里渊散射分布式光纤传感技术的出现恰恰填补了这些传统方法不能解决的弊端，该技术能够完成分布式的温度和应变测量，基于布里渊散射分布式光纤温度、应变系统能广泛应用于火灾预警监控，交通基础设施建设，运输管道等领域安全方面的监控。

1　基于布里渊散射的传感原理

1.1布里渊频移与温度和应变关系

光纤内部的声波速度νA和入射光的波长λ决定布里渊散射光频移νB的大小，即：

其中，n为介质的折射率。温度、应变的变化量可以由检测到的布里渊频移νB的变化量ΔνB获得。

式（1）内，νA可表示为：

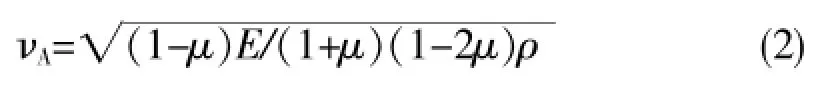
式中：E为光纤的弹性模量；μ为光纤的泊松比；ρ为光纤的密度。

在检测温度时，光纤中的应变和温度T不仅影响折射率n还影响光纤的密度ρ，同时也影响弹性模量E与泊松比μ，所以公式（2）可以改为：

假定：n（T，ε）、E（T，ε）、μ（T，ε）和ρ（T，ε），则公式(3)改为：

根据公式（4）可知，布里渊频移和光纤的温度、应变存在一定关联。

根据公式（4），应变ε=0时，布里渊频移跟温度的关系为：

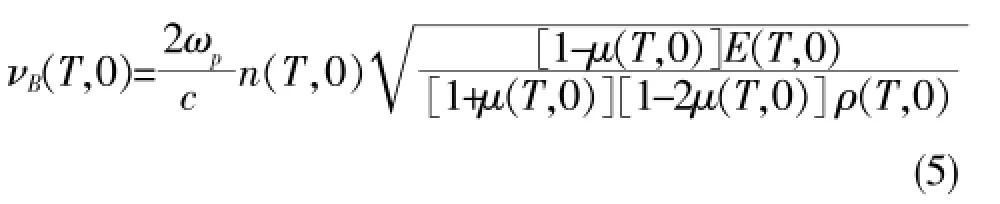
光纤上温度的热膨胀效应导致光纤的密度发生变化，产生的热光效应同样会导致光纤折射率发生变化，所以光纤中的参数值随着温度的改变而改变。对公式（5）展开得：

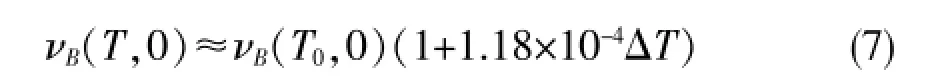
由上述可得，应变不存在时，温度与布里渊频移呈线性关系。

假设温度为常数T=T0时，布里渊频移与应变的关系式为：

假定ε=0时，对公式（8）进行展开，即：

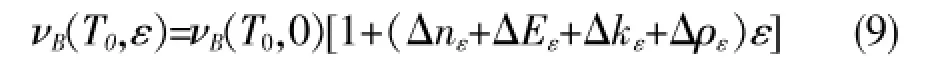
由上述可得，应变与布里渊频移是线性关系。

1.2布里渊强度与温度和应变关系

布里渊散射光的温度、应变会影响布里渊散射光强度大小，布里渊散射光强度的表示式为[1]：

公式（12）中，P0为入射光功率；S为背向布里渊散射系数[2]；αB为光纤损耗的系数；W为脉冲光宽度；ν为光纤介质里的光速。其中：

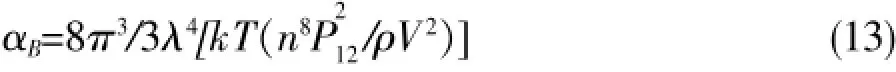
公式（13）中，λ表示真空下光的波长度；k为常数；T为绝对温度；P12为光纤弹性张量系数；ρ为光纤材料密度；V为光纤中的声速。其中：

其中，n是光纤中纤芯的折射率；A为光纤的有效面积。

由上述可得，布里渊强度和光纤的温度、应变存在一定关联。

假设温度为T，则表示式为：

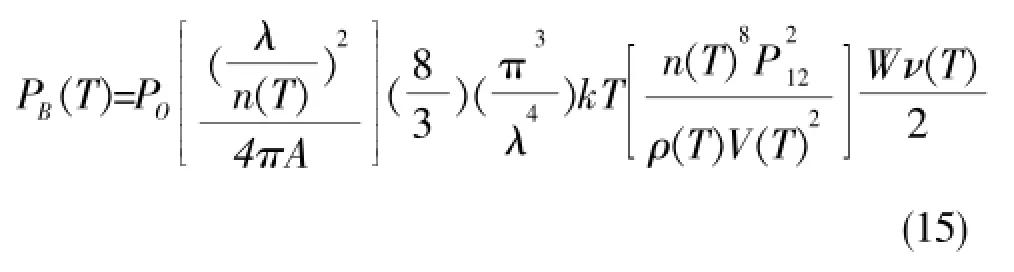
式中，参数值n、ρ、V对布里渊强度产生一定的影响。其中，λ=1550nm、T=298K、W=10ns、A=9.5*10-11m2、P12= 0.27、k=1.38*10-23J/K。布里渊强度跟温度的关系式为：

由上述可得，温度与布里渊强度呈线性关系。在应变情况下，参数值n、ρ、V的改变导致布里渊强度发生变化，即：

其中，λ=1550nm、T=298K、W=10ns、A=9.5*10-11m2、P12=0.27、k=1.38*10-23J/K、n（0）=1.46，且,n（ε）=n（0）+ 0.317ε，E（ε）=E（0）+5.75ε，K（ε）=K（0）+3.07ε、ρ（ε）=ρ（0）[1-（1-2k）ε]。则布里渊强度跟应变的表达式为：

PB（ε）=（2.19-21.51ε）*10-9（18）

由上述可得，应变与布里渊强度是线性关系。

2　基于BOTDR系统的性能分析

2.1温度、应变分辨率

用BOTDR技术对温度、应变的分布式进行检测，其中温度的分辨率、应变的分辨率指信噪比为1的情况下对应的应变或温度的变换数值[3]。温度、应变的分辨率由布里渊频移确定，即布里渊频移空间分辨率和信噪比的表示式[4]为：

式中，ΔνB表示布里渊散射线宽；ΔνP表示泵浦光波线宽。

由公式（19）得温度分辨率表示式如下：

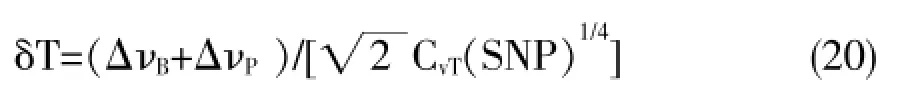
应变分辨率表示式如下：

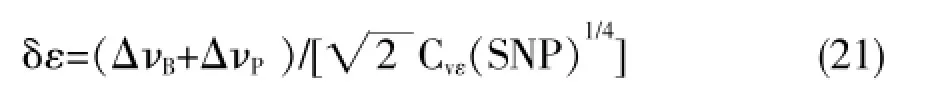
式中，δT为温度的灵敏度；δε为应变的灵敏度；CvT表示布里渊频移随着温度产生的变动系数值；Cvε表示布里渊频移随着应变产生的变动系数值。在通常情况下，布里渊散射线宽ΔνB远远大于泵浦光波线宽ΔνP，一般ΔνP忽略不计。

综上可知，随着信噪比的减少，温度、应变的分辨率也相应的减弱。

2.2动态范围

BOTDR系统的动态范围表示式为：

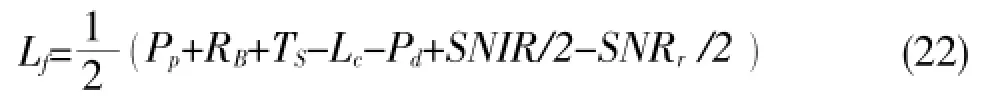
公式（22）中，Lf表示光纤损耗（dB）；RB表示布里渊散射因子 （dB）；Pp表示脉冲光波射入光纤峰值的功率（dBm）；Ts表示布里渊散射选择的比率 （dB）；Lc表示系统中的耦合器插入损耗 （dB）；Pd表示接收机最小的可探测光的功率；SNIR表示平均信噪比改善（dB）；SNRr表示温度、应变的信噪比。

其中，布里渊散射因子表示式为：

公式（23）中，S=0.25（λ/πna）2表示布里渊散射捕获系数；a表示光纤模场半径；

αB=7.1×10-31/λ4m-1表示常温下布里渊散射的系数；ν=2*108m/s为真空中光的速度；W为泵浦光波脉冲宽度。

公式（24）中，ΔνB为布里渊散射光频谱宽度；带通滤波器带宽B≥1/W。

在理论上，基于BOTDR系统的动态范围能够利用增大泵浦光波的功率Pp，以及把外差接收机灵敏度Pd提高的方法来完成。但是，实际实现时存在一定难度，BOTDR系统抗干扰的能力越好越可以增加BOTDR系统的动态范围。

3　基于布里渊散射的微弱信号算法分析

累加平均是相对比较简单、有效的一种信号处理算法，通过对待测信号点屡次采样并且对应累加，求其平均值，实现在噪声内复原信号的波形。现今较多见的两种累加平均算法：线性累加平均算法跟递推累加平均算法[5]。

3.1累加平均算法的线性描述

线性累加平均进程是大批次进行的算法。检测到m次数据依次对应相加，然后通过计算机求其平均值。

通常情况下，设输入信号f（t）是含有噪声，则一维的信号模型为：

其中，s（t）为功率W的有用信号；n（t）是0的平均值；方差是σ2的随机高斯白噪声；原来的幅度信噪比是S/N。

信号f（t）在每间隔T秒时间内进行一次取样，在一定的取样次数后，把信号进行累加平均。则在第点时的第K次的采样数值表示式：根据周期性信号，在相同状况内开始信号的扫描采样，起点tk设定为0，即：

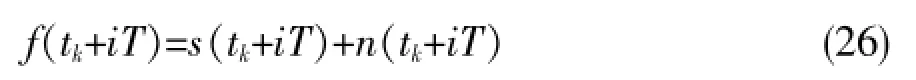
把扫描采样到的数值和储存的相对应单元的上一次采样数值进行线性累加，经过次采样后，第i点的数值表示式：

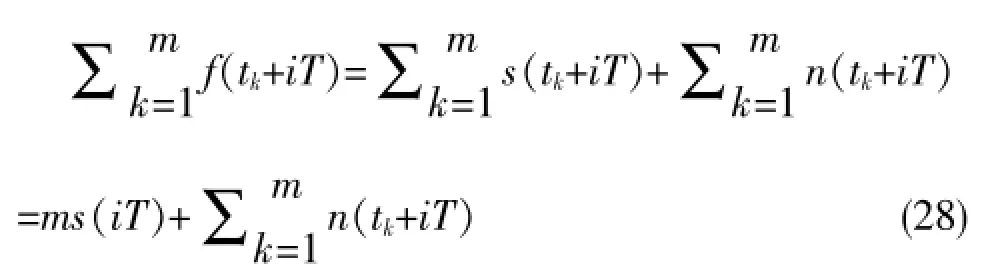
其中，噪声信号为：

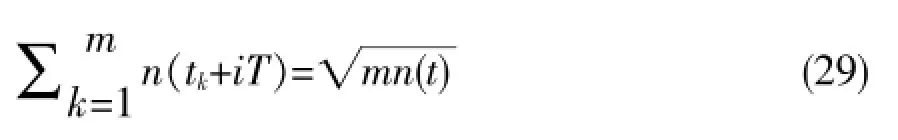
式中，n（t）代表噪声信号的有用数值，通过m次的累加平均后信噪比是：

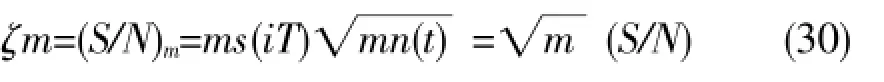
则，通过次的累加之后的信噪比和原来的信噪比存在的关联式如下：

信噪比的增益为：

根据上式可得，周期性的信号通过m次扫描取样，累加之后的信号信噪比升高到之前的m倍。所以，周期信号的信噪比和采样叠加数次有关，扫描采样叠加的数次越大，得到的信噪比改进性就会越好。在时间允许的情况下，累加平均达到一定的次数，就能够在大量的噪声中提炼到相对微小的信号。

3.2累加平均算法的递推描述

在实际操作的过程中，线性累加平均算法明显存在计算次数庞大，运算时间长，占据的系统信息空间大的缺点。所以，进一步的改进实验方法，每一次扫描采样得到数值时，应用上一次的平均结果进行再次刷新运算来得到全新的平均数值。

设定m-1时间之前的m-1个扫描取样数据的平均数值表示为f（m-1），时刻的平均数值是f（m），m时刻的取样数值是f（m），根据（28）公式可知：

当无数次扫描得到的采样数值时，平均数值的信噪比愈来愈大，检测到的微弱信号波形也变得更加清楚。

在一定的范围内随着平均次数的增大，新数据的作用相对应的减小。当平均次数增大到特定的范围之后，这个数值就接近于零，之后接着递推与平均也不会对信噪比起改良效用，平均的数值结果将不发生变化。

线性累加平均算法的方法相对简单，但是需要较长的时间来获取数据，数据的缓存区会出现过满溢出的情况；递推累加平均算法的方法相对于比较复杂，但是可以在较短的时间内获取数据，不存在溢出的现象。

3.3基于Morlet小波变换的包络检波算法

在实际的实验中，布里渊散射信号的包络不可能实现完全平滑的曲线，温度与应变的变化所引起的影响非常小，信号采集的检测方式不会实现完善系统功能的条件，运用叠加平均算法来增大系统的信噪比，但是同时必须付出较长的测量时间，所以采用小波变换算法不仅仅达到抑制噪声的作用而且还缩短了处理信号的时间。

Morlet小波是复数的小波，假定实部是ψar（x），虚部是ψai（x）。信号x(x)为Morlet小波变换：

Wx（a,b）=x(x)*ψa,b（x）=x(x)*ψar（x）+x(x)*jψai（x）（34）

Morlet小波经过变换后，小波实部的系数Re（wx（s, x）与虚部系数Im（wx（s，x）之间的相位差是90°。所以，根据解调的方式能够求得小波系数内的包络分量的关系为：

由两部分：带通滤波与幅值解调构成的信号包络检波，运用Morlet小波带通滤波的效用与它的实部与虚部相位差是九十度的特征来进行信号解调，完成利用Morlet小波变化对包络进行检波。

Morlet小波在不同尺度因子a的情况下完成信号的分析，能够求得在不同频带下信号的包络成分，即检测到信号中的包络，见图1。

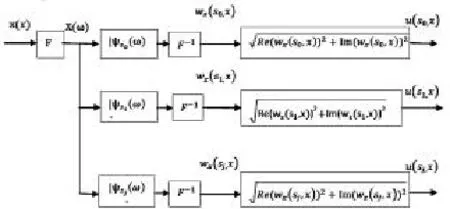
图1　基于Morlet小波的包络检波算法

图1是基于Morlet小波的包络检波算法：利用快速傅立叶变换把信号变换成频域信号，利用小波在频域结束算法，最后利用反快速傅立叶变换求得时域上的原始包络信号。为了更好地消除在信号里的随机噪声，还可以同时对包络信号进行叠加平均。

4　信号处理程序仿真实验结果

采用MATLAB7.1软件以及在LabVIEW的软件平台上，运用程序仿真的实验操作方式对布里渊散射信号进行分析，实现累加平均算法、基于Morlet小波变换算法的有效仿真。

4.1累加平均去噪测试实验仿真

本实验针对含有大量噪声的布里渊散射仿真信号进行累加平均去噪分析。首先，由指数函数和三个相互叠加的正弦波信号进行相乘，最终得到无噪声的布里渊散射信号，见图2。

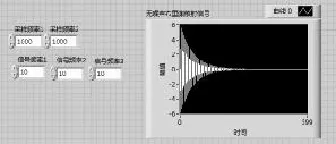
图2　无噪声布里渊散射信号

其次，在原来的基础上加上高斯白噪声，适当的写入采样频率、信号频率以及标准差参数得到含有大量噪声的布里渊散射信号，见图3。

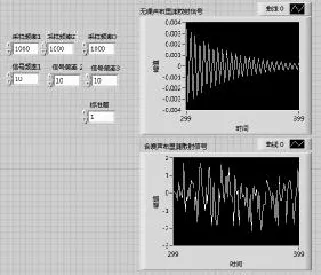
图3　含噪声布里渊散射信号

由图3可知，布里渊散射信号全部都被埋没在这个噪声中，现在运用叠加平均算法来抑制噪声，提取出去除噪声的布里渊散射信号，见图4。

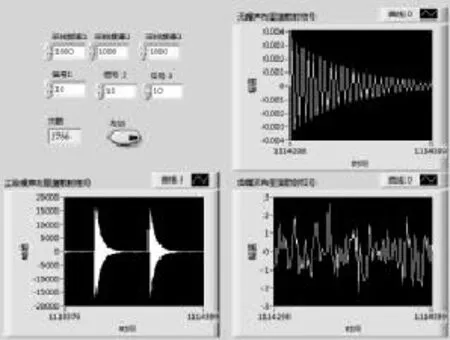
图4　　去除噪声布里渊散射信号

由图4可知，随着叠加次数的增多，得到的含噪声布里渊散射信号减少，随着叠加次数达到一定的程度时，就能够实现无噪声的布里渊散射信号提取。在时间允许的情况下，运用叠加平均算法来抑制噪声是具有可行性的。

4.2基于Morlet小波变换仿真实验

本实验采用MATLAB7.1软件进行操作，运用数值模拟的形式来完成对Morlet小波变换的信号处理。

数值模拟的前期仿真需要合理的信号源，本次仿真信号源是利用周期性的指数信号幅度被宽带调制信号调制产生。宽带调制信号在含有大量噪声的情况下，调制指数信号，将能够模拟得到含噪布里渊散射信号，见图5。

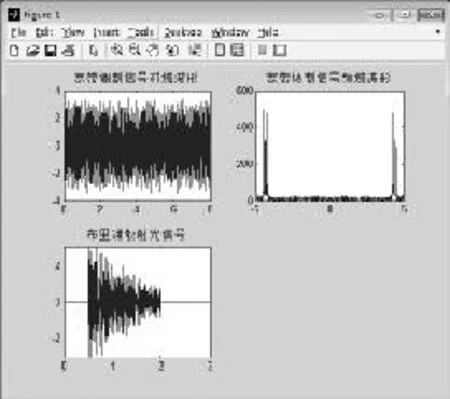
图5　布里渊散射信号信号源

基于Morlet小波的包络检波算法，再根据仿真的信号源，运用MATLAB7.1软件对其完成数值模拟操作，见图6。

图6中的图1表示含大量噪声的仿真的信号源，即含噪布里渊散射光信号；图6中的图2表示理想的信号，即运用仿真方式越好得到的信号越接近完美的信号；图6中的图3和图4是对含噪布里渊散射光信号进行快速傅里叶变换；图6中的图5是经过第一次仿真处理后得到的波形，存在大量的噪声干扰，图像严重失真；图6中的图6是经过第15次仿真处理后得到的波形，根据这个波形可以知道，经过多次处理后得到的信号波形图比较接近理想的波形，但是由于尺度因子的选择使得幅度值增加了。

虽然本次仿真会产生幅度的变化，但是因为信号源就是一个宽带调制信号，所以以幅度的大小变化来作为仿真的代价不存在很大的影响。

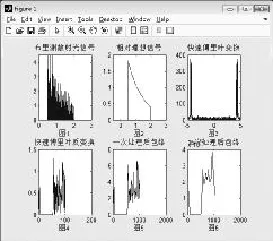
图6　　基于Morlet小波变换包络检波仿真

5　结语

由于存在设备上的不足，布里渊散射分布式光纤传感技术在本次探究中，只是在理论的基础上进行仿真实验完成了部分的成果，在接下来的研究中，需要在实际中构建实验系统。

在对含有噪声的信号源进行仿真时同样是基于理论的基础上进行搭建的一个仿真实验平台，在实际的应用中很难保证这个理论基础下的仿真是否达到实际的要求。虽然在对布里渊散射光信号的提取中具有一定的实用性和有效性，但是同样也存在很多的不足。鉴于时间的有限性，对于算法的研究存在不足，所以下一步，可以加大力度来研究其他性能更好，精确度更高的算法，从而达到以更高效率来实现对于含噪声信号的抑制和提取。

我国是自然灾害多发的国家，自然灾害导致的桥梁、隧道等大型结构建筑倒塌的问题，以及山体滑坡和泥石流等。对此进行防治和预报就显得尤为重要。布里渊散射分布式光纤传感技术具有点式光纤传感器体积小、耐腐蚀、抗电磁、灵敏度高外，更可以实现长距离、分布式监测[6]，形成传感监测网络，具有广阔的工程监测前景。

参考文献:

[1]黄民双,曾励,陶宝祺，等.分布式光纤布里渊散射应变传感器参数计算[J].航空学报,1999（2）:137-140.

[2] 欧中华.光纤中后向布里渊散射传感技术研究[D].成都：电子科技大学,2009.

[3]D.Garus,K.Krebber,R.Hereth.Distributed fiber optical sensors using Brillouin back scattering.SPIE,1995,25（10）:172-183.

[4] 李卓明.布里渊分布型光纤温度和应变传感技术研究[D].保定:华北电力大学,2007:22-26.

[5] 张硕.外差检测布里渊分布型光纤温度和应变传感及信号处理技术研究[D].保定：华北电力大学,2008.

[6]BAO Xiaoyi,CHEN Liang.Recent progress in distributedfiber optic sensors[J].Sensors,2012（12）:8601-8639.

中图分类号：TN929.11

文献标识码：A

文章编号：1674-2109（2015）06-0044-06

收稿日期：2015-03-08

基金项目：福建省中青年教师教育科研基金资助项目（JB14099），武夷学院国家级大学生创新训练计划项目（201210397007）。

作者简介：吴娟娟（1991-），女，汉族，在读本科，主要研究方向：光纤传输。

通讯作者：石贵民（1980-），男，汉族，讲师，主要研究方向：图像识别及网络信息系统。

Research on Extraction Of Sensing Information in Brillouin Scattering Distributed Fiber Optic Sensing System

WU Juanjuan，SHI Guimin，HU Shaobin，WU Longhuai，LIN Chennan
（School of Mathematics and Computer Science,Wuyi University,Wuyishan，Fujian 354300）

Abstract:This thesis has studied the mechanism of distributed optical fiber sensor,then the analysis,comparison of the characteristics and application of three different kinds of BOTDR,analyzes the Brillouin scattering distributed optical fiber sensing technology has become the inevitable development upsurge at home and abroad.On the LabVIEW software platform for cumulative average algorithm simulation results,at the same time use the mathematical software MATLAB simulation based on Morlet wavelet transform is realized.The research results of the paper in a certain extent for the deep exploration of Brillouin distributed optical fiber sensing system provides reference basis.

Key words:optical fiber sensing technology;Brillouin scattering;LabVIEW