基于扩张状态观测器的永磁同步电机滑模变结构位置伺服控制

陈强，陶亮，南余荣，董方（浙江工业大学 信息工程学院，浙江杭州 310023）

基于扩张状态观测器的永磁同步电机滑模变结构位置伺服控制

陈强，陶亮，南余荣，董方
（浙江工业大学 信息工程学院，浙江杭州 310023）

摘要：针对带有未知摩擦力矩和模型不确定的永磁同步电机位置伺服系统，提出两种基于扩张状态观测器的滑模变结构位置伺服控制策略。在系统存在状态未知和非线性特性有界的情况下，设计扩张状态观测器来观测系统的未知状态和非线性不确定项，并根据观测值设计降阶线性滑模控制和无抖振全阶滑模控制两种控制方法。仿真结果表明，降阶滑模控制方法控制精度较高且鲁棒性较强，而全阶滑模控制方法可以有效消除滑模控制中的抖振问题，便于实际应用。

关键词：永磁同步电动机；位置伺服系统；滑模变结构控制；扩张状态观测器

本文引用格式：陈强，陶亮，南余荣，等.基于扩张状态观测器的永磁同步电机滑模变结构位置伺服控制[J].新型工业化，2015，5（8）：17-25

Citation: CHEN Qiang, TAO Liang, NAN Yu-rong, et al. Sliding-mode Variable Structure Position Servo Control of Permanent Magnet Synchronous Motor Based on Extended State Observer[J]. The Journal of New Industrialization, 2015, 5（8）: 17-25.

0 引言

永磁同步电机（permanent magnet synchronous motor，PMSM）具有体积小、结构简单、气隙磁密高、转矩惯量大等优点，因此在诸如机器人，航天飞行器以及升降机等高性能系统的应用中已经取代直流电机，成为近些年来的研究热点[1-3]。由于永磁同步电机位置伺服控制系统本身具有非线性、时变性和强耦合性，且伺服对象往往也存在着较强的不确定性和扰动，因此，对于有高性能、高精度要求的伺服系统来说，传统的线性PID控制已不能满足其需求，尤其是当控制系统受到模型不确定和未知摩擦等非线性干扰时，控制器将很难兼顾动态响应和抗干扰能力的要求，从而导致控制性能进一步降低。

为提高系统的控制性能和鲁棒性，许多先进的非线性控制技术被应用于永磁同步电机伺服控制系统，如自抗扰控制[4]、自适应控制[5]、鲁棒控制[6]、滑模控制[7]和有限时间控制[8]等。其中，滑模控制（sliding-mode control，SMC）由于其对扰动和不确定性具有良好的鲁棒性，因而被广泛应用于各种伺服控制系统中。但是滑模控制中不连续项的存在，导致系统控制律中存在一定的抖振问题，严重影响了电机系统的精确定位和位置跟踪性能，甚至会对电机系统本身造成损害[9]。因此，在高性能永磁同步电机位置伺服系统中，如何削弱滑模控制中的抖振现象，是一个亟待解决的关键技术难题。

近些年，为了削弱传统滑模控制中的抖振问题，国内外已提出很多改进的滑模控制方法。文献[10]在控制器的设计过程中，采用了饱和函数来替代一般滑模控制中的切换项。该设计方法在削弱滑模抖振现象的同时，也减弱了传统滑模的鲁棒性能。文献[11]提出一种积分时变滑模控制器，在滑模面设计中引入误差的积分项和时变项，有效减小了滑模抖振并提高了误差收敛速度；文献[12]将滑模控制与自适应机制相结合，设计自适应滑模控制器，实时地更新切换增益，取得了较好的控制效果。然而，以上控制方法虽然在削弱滑模抖振方面均取得了一定效果，但却要求所有的系统状态是完全可测的，且未考虑摩擦力矩和模型不确定项引起的未知扰动对永磁同步电机控制性能的影响。

文献[13]和[14]分别将扰动观测器和扩张状态观测器与滑模控制相结合，用于永磁同步电机的调速控制。由于观测器对未知扰动具有一定的补偿作用，控制器增益被降低，从而在一定程度上减小了滑模抖振，但由于控制信号的不连续性，仍不能消除滑模控制器的抖振问题。近来，文献[15]提出了一种无抖振滑模控制方法，该控制器是一种全阶滑模控制器，与传统的降阶滑模控制器相比，控制信号是连续的，能够有效避免滑模抖振问题。

本文针对带有未知摩擦力矩和模型不确定项的永磁同步电机位置伺服系统，提出两种基于扩张状态观测器的永磁同步电机滑模变结构位置伺服控制方法。设计扩张状态观测器来观测系统状态及摩擦力矩和模型不确定项等非线性特性，并使用观测值来设计降阶线性滑模控制器和无抖振全阶滑模控制器，实现电机输出位置对期望轨迹的快速精确跟踪。

1 永磁同步电机数学模型

在d/q旋转坐标系下，永磁同步电机的数学模型可表示为：

其中，ud、uq分别为d、q轴上的电压分量；id、iq为d、q轴上的电流分量；J为系统的转动惯量；R为定子电阻；pn为极对数；Ld、Lq分别为d、q轴上的电感分量； Ψf为永磁体基波励磁磁链；ω为转子的角速度；Te为电磁转矩；TL为负载转矩； B为摩擦系数。

为了实现伺服系统的高性能控制，在实际应用中，常采用id=0的转子磁场定向控制方法，其永磁同步电机位置伺服系统框图如图1所示。

图1 永磁同步电机位置伺服控制系统框图Fig.1 Schematic diagram of PMSM position control system

由式（1）-（3），可得永磁同步电机位置环的二阶动态方程为

本文的控制目的为通过设计控制信号 ()ut，使得永磁同步电机的实际输出位置y能够精确跟踪期望轨迹yd。

2 扩张状态观测器设计

其中，β1,β2,β3＞0为观测器增益.fal(·)为原点附近具有线性段的连续幂次函数，表达式为：

由文献[16]，[17]可知，当选择适当的参数βi，函数fal(·)可以使得观测器状态 zi→xi，即：观测|x－z|≤l l＞0误差可以收敛到，其中为很小的正数。

3 滑模变结构控制

定义跟踪误差为

则e的一阶和二阶导数分别为

和

3.1 降阶滑模控制器设计

由式（9）和式（10），降阶线性滑模面可设计为

对式（12）求导，由式（9）-（11）可得

由式（13），基于扩张状态观测器（7）的降阶滑模控制器可设计为

3.2 全阶滑模控制器设计

根据式（9）-（11），设计如下全阶滑模面

其中，10λ＞和20λ＞为控制参数。

将式（9）-（11）代入式（15），可得

由式（16），基于扩张状态观测器（7）的全阶滑模控制器可设计为

由式（17）-（20）可以看出，通过加入一阶滤波器1/(s+T)以后，只有u2中含有滑模切换项sgn(s)，而实际控制信号u中并不包含该切换项。因此，该控制器能够消除由于滑模切换项而造成的抖振问题。

将式（17）-（20）代入式（16）中，有

设计与研究

其中，d(x,z)=(x3－z3)+λ2(x2－z2)+λ1(x1－z1)，且满足d(x,z)≤ld，ld=l3+λ2l2+λ1l1。

对式（21）求导可得

3.3 稳定性证明

以下引理和定理给出了系统（5）的稳定性证明。

引理1[2]：假设存在一个连续、正定的函数()Vt，满足以下微分方程：

其中，0α＞和01η＜＜是常数。则对于任意给定的t0，存在一个有限时间t1，使得以下不等式和等式成立：

和

定理1：给定不确定永磁同步电机位置伺服系统（5）和降阶滑模面（12），设计扩张状态观测器（7）和控制器（14），则当控制参数k1满足k1≥|ε3|+λ0|ε2|时，跟踪误差e将稳定收敛至零点。

证明：针对系统（6），构建如下Lyapunov函数

对V求导，由式（12）-（14）可得

因此，当k1满足k1≥|ε3|+λ0|ε2|时，有

11时，V(t)=0恒成立，即滑模面s1可在有限时间内快速稳定地收敛至零点。

由式（12）可得，在滑模面s1=0上有e.+λ0e=0恒成立，因此，当t→∞时，跟踪误差e将稳定收敛至零点。

定理2：针对永磁同步电机伺服控制系统（5），设计全阶滑模面（15）及控制器（17）-（20），当控制参数kd和kT分别满足kd≥|d.(x,z)|，kT≥Tld时，跟踪误差e将稳定收敛至零点。

证明：针对系统（5），构建如下Lyapunov函数

对V求导，由式（17）-（20）可得

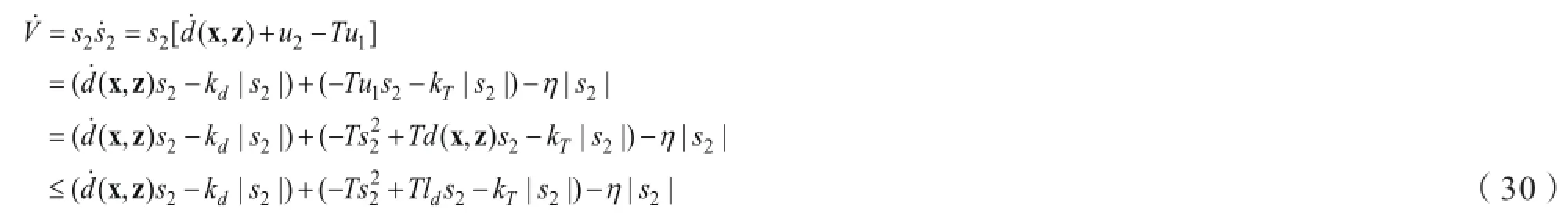
当kd和kT分别满足时，可得

由式（15）可得，在滑模面s2=0上有：

式（32）可以进一步改写为：

其中，0＜λ0＜λ2且满足(λ2－λ0)λ0=λ1。

定义

则式（33）可以改写为

因此，当t→∞时，可得0χ→成立，由式（34）可以推导得出跟踪误差e将稳定收敛至零点。

4 仿真研究及结果

设计与研究

为了分析和对比基于扩张状态观测器的降阶滑模控制（reduced-order sliding mode control based on extended state observer，RSMC+ESO）与基于扩张状态观测器的全阶滑模控制（full-order sliding mode control based on extended state observer，FSMC+ESO）两种控制方法的优劣性，本节对永磁同步电机位置伺服控制系统进行了仿真研究。仿真中PMSM系统、控制器和扩张状态观测器参数分别给定如下。

PMSM参数设置为：额定功率P=0.2kW，额定转速ω=3000r/min，永磁体磁链Ψf=0.371Wb ，极对数Pn=4，d-q轴电感Ld=Lq=30mH，转动惯量J=0.17kg·cm2，粘性阻尼系数B=0.001N·m/(r/min)；扩张状态观测器参数设置为：β1=β2=β3=100，δ=0.01，b0=10；控制器参数分别设置为：k1=k2=20，λ0=λ2=2，λ1=5，T=0.01。为便于两种控制方法的比较，本节分别针对正弦信号和阶跃信号的跟踪效果进行对比，对比效果如图2和图3所示。

图2给出了当负载TL=2Nm，跟踪位置为正弦信号时，采用RSMC+ESO与FSMC+ESO两种控制方法的正弦曲线跟踪效果对比。其中，图2（a）和图2（b）为分别采用两种控制方法时的位置跟踪曲线和跟踪误差曲线对比，图2（c）为两种控制方法的控制信号对比。图2（d）为两种方法中扩张状态观测器的观测误差对比。从图2（a）可以看出，采用FSMC+ESO方法比RSMC+ESO方法有更快的跟踪速度，但从图2（b）和图2（c）可以看出，FSMC+ESO方法的正弦曲线跟踪的稳态误差虽然略大于RSMC+ESO方法，但控制信号的抖振却明显小于RSMC+ESO方法。

图2 两种控制方法的正弦波跟踪对比Fig.2 Sine wave tracking comparison of two control methods

图3 两种控制方法的阶跃跟踪对比Fig.3 Step tracking comparison of two control methods

为进一步比较两种控制方法的优缺点，图3给出了初始负载为空载，位置给定为阶跃信号时的跟踪效果和控制信号。其中，图3（a）给出了采用RSMC+ESO与FSMC+ESO两种控制方法的阶跃信号跟踪效果，并且在t=10s时突加了负载扰动TL=3Nm，图3（b）为两种控制方法的控制信号。从图3（a）可以看出，在t=10s时突加负载TL=3Nm以后，RSMC+ESO方法能够更快地做出反应并及时跟踪上位置给定，而FSMC+ESO方法则较慢，系统产生相对较大的位置跟踪滞后。因此，RSMC+ESO方法比FSMC+ESO方法有更好的鲁棒性。然而，图3（b）给出的控制增益曲线表明，RSMC+ESO方法的控制信号抖振较大，而FSMC+ESO方法的控制信号几乎无抖振问题。

5 结论

本文考虑摩擦力矩和模型不确定项引起的未知扰动对永磁同步电机控制性能的影响，设计两种基于扩张状态观测器的永磁同步电机滑模变结构位置伺服控制方法。 采用扩张状态观测器来观测系统状态及摩擦力矩和模型不确定项等非线性特性，并使用观测值来设计控制和全阶滑模控制方法，保证电机输出位置精确跟踪期望轨迹。仿真结果表明，RSMC+ESO方法具有更好的稳态跟踪精度和鲁棒性，而FSMC+ ESO方法基本无抖振问题，便于实际应用。

参考文献

[1] 唐任远. 现代永磁电机理论与设计[M]. 北京： 机械工业出版社，2000. R Y Tang. Modern permanent magnet machines theory and design[M]. Beijing： Machinery Industry Press，2000.

[2] Chen Q，Yu L，Nan Y R. Finite-time tracking control for motor servo systems with unknown dead-zones[J]. Journal of Systems Science and Complexity，2013，26（6）： 940-956.

[3] Na J，Chen Q，Ren X M，et al. Adaptive prescribed performance motion control of servo mechanisms with friction compensation[J]. IEEE Transactions on Industrial Electronics，2014，61（1）： 486-494.

[4] 邵立伟，廖晓钟，张宇河，等. 自抗扰控制器在永磁同步电机控制中的应用[J]. 北京理工大学学报，2006，26（4）： 326-329. L W Shao，X Z Liao，Y H Zhang，et al. Active disturbance rejection controller scheme for permanent magnetic synchronous motor [J]. Transactions of Beijing Institute of Techonlogy，2006，26（4）： 326-329.

[5] 陈强，吴根忠，叶雷. 永磁同步电机变负载自适应神经网络控制[J]. 新型工业化，2014，4（4）：17-22. Q Chen，G Z Wu，L Ye. Adaptive neural control of permanent magnet synchronous motor with variable load[J]. The Journal of New Industrialization，2014，4（4）： 17-22.

[6] 林立，黄苏融. 永磁同步电机系统线性化H_∞鲁棒控制[J]. 电机与控制学报，2009，13（4）： 541-552. L Lin，S R Hang. Robust control with linearization technique for interior permanent magnet synchronous motor servo system[J]. Machines and Control，2009，13（4）： 541-552.

[7] 许叙遥，林辉. 基于动态滑模控制的永磁同步电机位置速度一体化设计[J]. 电工技术学报，2014，29（5）： 77-82. X Y Xu，H Lin. Integrated design for permanent magnet synchronous motor servo systems based on dynamic sliding mode control[J]. Transactions of China Electrotechnical Society，2014，29（5）： 77-82.

[8] 刘慧贤，丁世宏，李世华，等. 永磁同步电机位置伺服系统的有限时间控制[J]. 电机与控制学报，2009，13（3）： 424-430. H X Liu，S H Ding，S H Li，et al. Finite-time control of PMSM position servo system[J]. Electric Machnies and Control，2009，13（3）：424-430.

[9] 黄佳佳，周波，李丹，等. 滑模控制永磁同步电动机位置伺服系统抖振[J]. 电工技术学报，2009，24（11）： 41-47. J J Hang，B Zhou，D Li，et al. Sliding mode control for permanent magnet synchronous motor servo system[J]. Transactions of China Electrotechnical Society，2009，24（11）： 41-47.

[10] Utkin V. Sliding modes in control and optimization [M]. Berlin，Germany： Springer-Verlag，1992.

[11] 陈振，耿洁，刘向东. 基于积分时变滑模控制的永磁同步电机调速系统[J]. 电工技术学报，2011，26（6）： 56-61. Z Chen，J Geng，X D Liu. An integral and exponential time-varying sliding mode control of permanent magnet synchronous motors[J]. Transac-tions of China Electrotechnical Society，2011，26（6）： 56-61.

[12] 付培华，陈振，丛炳龙，等. 基于反步自适应滑模控制的永磁同步电机位置伺服控制系统[J]. 电工技术学报，2013，28（9）： 288-293. P H Fu，Z Chen，B L Cong，et al. A position servo system of permanent magnet synchronous motor based on back-stepping adaptive sliding mode control[J]. Transactions of China Electrotechnical Society，2013，28（9）： 288-301.

[13] 张小华，刘慧贤，丁世宏，等. 基于扰动观测器和有限时间控制的永磁同步电机调速系统[J]. 控制与决策，2009，24（7）： 1028-1032. X H Zhang，H X Liu，S H Ding，et al. PMSM speed-adjusting system based on disturbance observer and finite-time control[J]. Control and Decision，2009，24（7）： 1028-1032.

[14] Li S H，Zhou M M，Yu X H. Design and Implementation of terminal sliding mode control method for PMSM speed regulation system[J]. IEEE Transactions on Industrial Informatics，2013，9（4）： 1879-1891.

[15] Feng Y，Han F L，Yu X H. Chattering-free full-order sliding-mode control[J]. Automatica，2014，50（4）： 1310-1314.

[16] 韩京清. 自抗扰控制技术：估计补偿不确定因素的控制技术[M]. 北京： 国防工业出版社，2008. J Q Han. Active disturbance rejection control technique： the technique for estimating and compensating the uncertainties[M]. Beijing：National Defense Industry Press，2008.

[17] 代志纲，岳巍澎，隋晓雨，等. 自抗扰控制技术的原理剖析[J]. 新型工业化，2015，5（1）：49-58. Z G Dai，W P Yue，X Y Sui，et al. Dissection on the principle of active disturbance rejection control technology[J]. The Journal of New Industrialization，2015，5（1）： 49-58.

DOI：10.3969/j.issn.2095-6649.2015.08.004

*基金项目：国家自然基金资助项目（61403343）

作者简介：陈强（1984-），男，讲师，博士，主要研究方向：非线性伺服系统建模与控制；陶亮（1990-），男，学生，硕士，主要研究方向：参数辨识与伺服系统摩擦建模补偿；南余荣(1966-)，男，教授，博士，主要研究方向：电力传动及其自动化，运动控制;董方（1991-），男，学生，硕士，主要研究方向：多电机同步驱动系统

Sliding-mode Variable Structure Position Servo Control of Permanent Magnet Synchronous Motor Based on Extended State Observer

CHEN Qiang, TAO Liang, NAN Yu-rong, DONG Fang
(College of Information Engineering, Zhejiang University of Technology, Hangzhou, 310023)

ABSTRACT:In this paper, two sliding-mode variable structure control (SMVSC) methods are proposed for permanent magnet synchronous motor (PMSM) servo control system with unknown friction torque and model uncertainty based on extended state observer (ESO). In the case of unknown system states and the bounded nonlinear characteristics, the ESO is designed to observe the unknown system states and nonlinear uncertainties, and then a reduced-order sliding mode control (RSMC) and a full-order sliding mode control (FSMC) schemes are both presented based on the ESO observations. Simulation results show that the RSMC performs better than FSMC with respect to tracking accuracy and robustness to load, while FSMC can effectively eliminate the chattering problem, which is more convenient for practical applications.

KEYWORDS:Permanent magnet synchronous motor; Position servo system; Sliding-mode variable structure control; Extended state observer