线性代数课程中 “逆矩阵”的教学设计与思考

文/涂正文 吴艳秋 彭扬

逆矩阵是线性代数中非常抽象的概念，学生学习难度较大，本文结合笔者的教学实践，浅谈逆矩阵的教学设计。

一、引入

在数的运算中我们知道，当数a≠0时，除以数a相当于乘上这个数的倒数a-1，有了倒数这一概念之后，除法运算全部转化为乘法运算。对于矩阵而言，是否也存在类似于倒数作用的一个矩阵，而且有了该矩阵，就相当于有了矩阵的除法运算呢?类似于倒数作用的矩阵又该如何去定义呢?

引入的设计意图:可将抽象的陌生的逆矩阵的概念与熟悉的数的除法运算类比，将陌生转化为熟悉，降低学生的理解难度。

二、新课

定义1 设A为n阶方阵，若存在n阶方阵B，使得

AB=BA=I

则称A是可逆矩阵，且称B为A的逆矩阵;若B不存在，则称A是不可逆矩阵。

首先指出对于n阶方阵A而言，满足AB=BA=I的矩阵B是唯一的。

将A的唯一的逆矩阵记为A-1，读作A的逆，即有AA-1=A-1A=I。

设计意图:定义1给出了判定n阶方阵可逆以及求解逆矩阵的方法——待定系数法。

例1 判定下列矩阵是否可逆?若可逆，求其逆矩阵。

例1 的设计意图:例1采用的是待定系数法，依赖于解线性方程组，不仅判断出n阶方阵A是可逆的，同时当n阶方阵A可逆时，可求出它的逆矩阵。但是随着方阵A阶数的增大，此法的计算量势必增大。

2、逆矩阵的判定定理

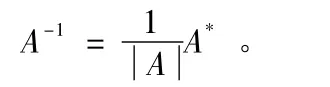
例2的设计意图:利用2阶方阵的伴随矩阵的口诀“主对调，次变号”，教会学生快速写出2阶方阵的逆矩阵。

3、逆矩阵的性质及结论

(1)若n阶方阵A可逆，则A-1也可逆，且 A-(1)-1=A;

(3)若n阶方阵A可逆，则AT也可逆，且(AT)-1= A-(1)T;

(4)若n阶方阵A、B都可逆，则乘积AB也可逆，且( A B)-1=B-1A-1;

(5)若n阶方阵A可逆，且AB=AC，则B=C;

(6)若n阶方阵A可逆，且AB=O，则B=O。

设计意图:与教材相比较，教学过程中增加了结论 (5)(6)，这样的教学设计，主要与矩阵乘法的运算规律:

若AB=AC，A≠O，不能推出B=C;若AB=O，A≠O，不能得到A≠O，B=O。

4、利用逆矩阵求解矩阵方程

含有未知矩阵X的方程称为矩阵方程，有以下三种情况:

(1)矩阵方程AX=B，其中A为n阶可逆方阵，则AX=B有唯一解X=A-1B;

(2)矩阵方程XA=B，其中A为n阶可逆方阵，则XA=B有唯一解X=BA-1;

(3)矩阵方程AXB=C，其中A，B分别为n阶和m阶可逆方阵，则AXB=C有唯一解X=A-1CB-1.

设计意图:与引入呼应，强调有了逆矩阵相当于矩阵有了类似于数的除法运算。

总结:线性代数课程教学，必须重视该课程的抽象性带给学生的困扰，教学实践中一定要将陌生的矩阵知识与熟悉的数的相关知识结合进行类比学习，降低学生的学习难度。

［1］同济大学数学系.工程数学--线性代数 ［M］.2007年5月第五版.

［2］北京大学数学系几何与代数教研室.高等代数 ［M］.2004年第三版.